数据挖掘--风电机组异常数据识别与清洗

一、赛题背景

（一）背景

风能是一种环境友好且经济实用的可再生能源。中国是世界排名第一的风力发电国家、新装风力发电设备装机容量最大的国家，并且保持快速增长。由于风力发电正处于飞速发展阶段，风电场数量和规模不断扩大，然而受地理条件和环境因素限制，风电场多位于偏僻遥远的平原、山区或海上，因此为风电公司引入SCADA系统（数据采集与监视控制系统）对风电场群的日常运行进行集中监控、调度和管理，但风电机组受设备、环境、运行状态等因素影响，SCADA系统实时采集的风机运行数据会存在有大量异常值和缺失值，这些“脏数据”的存在严重影响后续的风电机组状态分析、故障诊断等功能。因此，识别并排除风电机组的异常数据具有重要的探究意义。

（二） 赛题任务

依据提供的8台风力电机1年的10min间隔SCADA运行数据，包括时间戳信息、风速信息、风机转速信息和功率信息等，利用机器学习相关技术，建立鲁棒的风电机组异常数据检测模型，用于识别并剔除潜在的异常数据，提高数据质量。
此任务未给出异常数据标签，视为聚类任务，为引导选手向赛题需求对接，现简单阐述异常数据定义。异常数据是由风机运行过程与设计运行工况出现较大偏离时产生，如风速仪测风异常导致采集的功率散点明显偏离设计风功率。

（三）数据介绍

数据来源自某风电场群的1年SCADA真实运行数据，主要有4个维度信息分别为时间戳、风速、功率和风轮转速，并且给出风机参数说明罗列了各风机的风轮直径、额定功率和风轮转速范围等信息，该数据集从风机实际生产过程中收集，是风机在实际工况条件下运行的典型结果，因此每台风机的原始数据中都包含大量异常数据点，该数据集与风机SCADA系统异常数据检测应用场景相适配。
注：赛题链接

二、赛题解析

首先，学习方式是无监督的方法，不是简单的二分类问题，使得一些如xgb树、CNN网络等之类的成熟模型将无法使用，除非通过半监督的方式进行人为打标，但这样风险过大，易过拟合。
其次，数据的特征太少了，每一个电机只有【‘时间戳’,‘风速’,‘功率’,‘风轮转速’】四种特征，并且该数据集为时间序列，古可以做很多的特征衍生。
最后，可以通过一定的风电机组发动机实际物理模型进行数学意义上的异常分析，或通过图像法来人为选定异常值，当然，我们也可以按照比赛要求使用经典的无监督模型进行聚类分析。

本文主要从以下几个方面介绍：

• 第一部分对数据做特征处理；
• 第二部分将分别从单特正和多组联合特征直观展示每个风机的数据特征分布；
• 第三部分基于规则筛选异常值；
• 第四部分建立多个无监督聚类模型进行异常数据监测；如：DBSCAN、IsolationForest、Gaussian distribution；
• 第五部分基于物理学理论模型建立风速和功率的回归模型，设定阀值确定异常数据。

三、特征处理

（一） 读取数据

import pandas as pd
import warnings
import numpy as np
import matplotlib.pyplot as plt
warnings.filterwarnings('ignore')

plt.rcParams['font.sans-serif'] =['SimHei'] ##显示中文
plt.rcParams['axes.unicode_minus'] = False

data = pd.read_csv('./data/dataset.csv')

查看数据特征信息

data.info()

data.head()

（二）特征工程

特征工程没有什么标准规则来设计新的特征，可以根据业务设计出新的特征，也可以自己再不了解业务的情况下，设计出新的特征。以下设计的特征也是时间序列常用的一些特征衍生。

1.单位风速和单位风机转速的功率

data['per_windspeed_power'] = data['Power']/(data['WindSpeed']+0.0112) ###+0.0112防止分母为0
data['per_rotorspeed_power'] = data['Power']/(data['RotorSpeed']+0.0112)

2.单位功率的风速和单位功率的风机转速

data['per_power_windspeed'] = data['WindSpeed']/(data['Power']+0.0112)
data['per_power_rotorspeed'] = data['RotorSpeed']/(data['Power']+0.0112)

3.时间特征
根据时间特征，提取年、月、日、时、分、星期、工作日等特征

def process_dt(df=None,dt=None):
    """
    df:dataFrame类型
    dt：日期类型列名，字符串
    """
    df['dateTime'] = pd.to_datetime(df[dt])
    df['day'] = df['dateTime'].dt.day
    df['hours'] = df['dateTime'].dt.hour
    df['minute'] =df['dateTime'].dt.minute
    return df
data = process_dt(df=data,dt='Time')
data = data.sort_values(['WindNumber','dateTime']).reset_index(drop=True)

4.计算日志丢失率
因为分机每十分钟生成一条运行数据，再某些情况下，可能会产生数据丢失，因此，有必要计算日志数据的每个时间点的丢失率。

def generate_init(df=data,init_col_name=list(),group_col_name=None,dt=None):
	"""
	计算每一个风机最初特征值
	"""
    init_data =data[[group_col_name]+init_col_name].sort_values(dt).drop_duplicates([group_col_name]).reset_index(drop=True)
    init_data.rename(columns=dict(zip(init_col_name,['init_'+col for col in init_col_name])),inplace=True)
    return init_data

init_data=generate_init(data,['dateTime'],group_col_name='WindNumber',dt='dateTime')
data = data.merge(['init_dateTime','WindNumber']],how='left',on=['WindNumber'])

def stat_log_loss(df,group_col_name=None,date=None,init_date=None):
    """
    计算数据日志损失率,正常情况下，一台风机按照每10分中记录一次日志频率。
    """
    df[date]=pd.to_datetime(df[date])
    df[init_date]=pd.to_datetime(df[init_date])
    tmp =df[[group_col_name]]
    tmp['count']=10
    df['log_cumsum'] = tmp.groupby([group_col_name])['count'].transform(np.cumsum)
    df['miss_log_rate'] = 1-df['log_cumsum']/(((df[date]-df[init_date])/pd.Timedelta(1, 'min')).fillna(0).astype(int)+0.0001)
    return df

data=stat_log_loss(data,group_col_name='WindNumber',date='dateTime',init_date='init_dateTime')

5.差分特征

def diff(df,diff_feature_list=list(),group_col_name='WindNumber',diff_number=list()):
    tmp = df.loc[:,[group_col_name]+diff_feature_list].groupby(group_col_name)
    for i in diff_number:
        diff_colname =['diff_{}_'.format(i)+col for col in diff_feature_list]
        df[diff_colname] = tmp[diff_feature_list].shift(0)-tmp[diff_feature_list].shift(i)
    del tmp
    return df

data=diff(data,['WindSpeed','Power','RotorSpeed'],diff_number=[1,2,3,6,12])

6.变化率

def gct_change(df,gct_col=list(),group_col_name='WindNumber'):
    tmp= df.groupby([group_col_name])
    for col in gct_col:
        df['pct_'+col] = tmp[col].pct_change(fill_method='ffill')
        
    del tmp 
    return df
    
data=gct_change(data,gct_col=['WindSpeed','Power','RotorSpeed'])

7.指数平滑

def ewm_calculate(df,ewm_col_list=list(),group_col_name='WindNumber',spans=list()):
    """
    指数平滑，取mean和std
    """
    tmp = df.groupby([group_col_name])
    for i in spans:
        for col in tqdm(ewm_col_list):
            df['ewm_'+str(i)+"_"+col+'_mean'] =tmp[col].transform(lambda x: pd.Series.ewm(x,span=i).mean())
            df['ewm_'+str(i)+"_"+col+'_std'] =tmp[col].transform(lambda x: pd.Series.ewm(x,span=i).std())
    del tmp
    return df

data = ewm_calculate(data,ewm_col_list=['WindSpeed','Power','RotorSpeed'],group_col_name='WindNumber',spans=list([3,6,12]))

8.缺失值填充

##按每组均值填充缺失值
for column in list(data.columns[data.isnull().sum()>0]):
    data[column] =data[["WindNumber",column]].groupby("WindNumber").\
    transform(lambda x:x.fillna(x.mean()))
##或直接填充为0值
for column in list(data.columns[data.isnull().sum()>0]):
    data[column].fillna(0,inplace=True)

做完特征工程后，特征扩充到如下：

features	Value	not null	type
WindNumber	497837	non-null	int64
Time	497837	non-null	object
WindSpeed	497837	non-null	float64
Power	497837	non-null	float64
RotorSpeed	497837	non-null	float64
dateTime	497837	non-null	datetime64[ns]
day	497837	non-null	int64
hours	497837	non-null	int64
minute	497837	non-null	int64
init_dateTime	497837	non-null	datetime64[ns]
log_cumsum	497837	non-null	int64
miss_log_rate	497837	non-null	float64
per_windspeed_power	497837	non-null	float64
per_rotorspeed_power	497837	non-null	float64
per_power_windspeed	497837	non-null	float64
per_power_rotorspeed	497837	non-null	float64
diff_1_WindSpeed	497837	non-null	float64
diff_1_Power	497837	non-null	float64
diff_1_RotorSpeed	497837	non-null	float64
diff_2_WindSpeed	497837	non-null	float64
diff_2_Power	497837	non-null	float64
diff_2_RotorSpeed	497837	non-null	float64
diff_3_WindSpeed	497837	non-null	float64
diff_3_Power	497837	non-null	float64
diff_3_RotorSpeed	497837	non-null	float64
diff_6_WindSpeed	497837	non-null	float64
diff_6_Power	497837	non-null	float64
diff_6_RotorSpeed	497837	non-null	float64
diff_12_WindSpeed	497837	non-null	float64
diff_12_Power	497837	non-null	float64
diff_12_RotorSpeed	497837	non-null	float64
pct_WindSpeed	497837	non-null	float64
pct_Power	497837	non-null	float64
pct_RotorSpeed	497837	non-null	float64
pct_miss_log_rate	497837	non-null	float64
ewm_3_WindSpeed_mean	497837	non-null	float64
ewm_3_WindSpeed_std	497837	non-null	float64
ewm_3_Power_mean	497837	non-null	float64
ewm_3_Power_std	497837	non-null	float64
ewm_3_RotorSpeed_mean	497837	non-null	float64
ewm_3_RotorSpeed_std	497837	non-null	float64
ewm_6_WindSpeed_mean	497837	non-null	float64
ewm_6_WindSpeed_std	497837	non-null	float64
ewm_6_Power_mean	497837	non-null	float64
ewm_6_Power_std	497837	non-null	float64
ewm_6_RotorSpeed_mean	497837	non-null	float64
ewm_6_RotorSpeed_std	497837	non-null	float64
ewm_12_WindSpeed_mean	497837	non-null	float64
ewm_12_WindSpeed_std	497837	non-null	float64
ewm_12_Power_mean	497837	non-null	float64
ewm_12_Power_std	497837	non-null	float64
ewm_12_RotorSpeed_mean	497837	non-null	float64
ewm_12_RotorSpeed_std	497837	non-null	float64

四、数据可视化

（一）单特征的数据可视化

1.风速密度直方图

plt.figure(figsize=(15,18))
font = {'weight':'normal','size':10}
for  i in list(range(1,13)):
    ax=plt.subplot(4,3,i)
    ax.hist(data.loc[data['WindNumber']==i,'WindSpeed'],range=(-0.1,16.5),bins=50,density=True)
    plt.xlabel("Power(kw)",fontdict=font)
    plt.ylabel("Probability",fontdict=font)
    plt.title(r"Histogram of $windNumber-%s WindSpeed"%i,fontdict=font)
    plt.tight_layout()
plt.savefig('./pic/Power_WindSpeed.png',bbox_inches='tight',pad_inches=0.5,dpi=300)

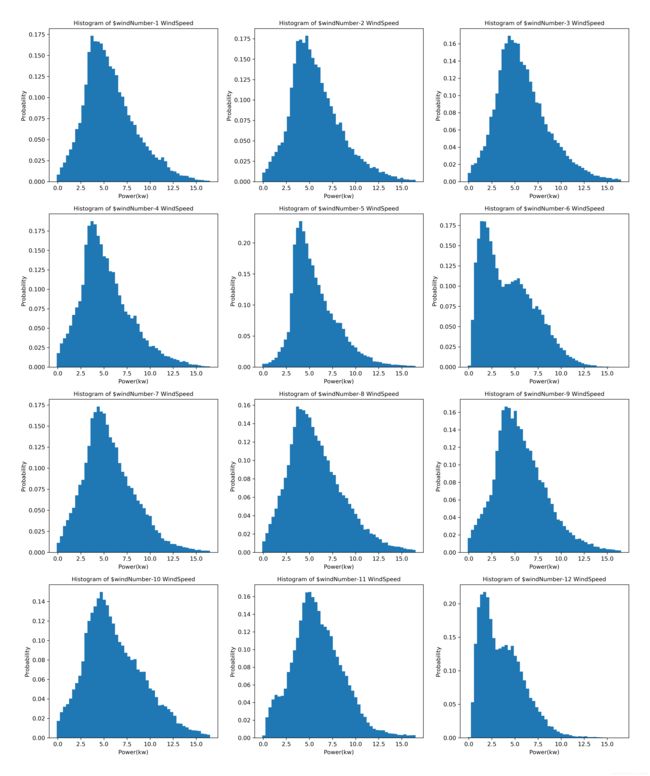可以看出大部分风机的样本风速呈现正太分布，只有6号风机和12号风机呈现正偏态。

2.风机转速密度直方图

plt.figure(figsize=(15,18))
font = {'weight':'normal','size':10}
for  i in list(range(1,13)):
    ax=plt.subplot(4,3,i)
    ax.hist(data.loc[data['WindNumber']==i,'RotorSpeed'],range=(-0.1,16.5),bins=50,density=True)
    plt.xlabel("RotorSpeed(m/s)",fontdict=font)
    plt.ylabel("Probability",fontdict=font)
    plt.title(r"Histogram of $windNumber-%s RotorSpeed"%i,fontdict=font)
    plt.tight_layout()
plt.savefig('./pic/test.png',bbox_inches='tight',pad_inches=0.5,dpi=300)

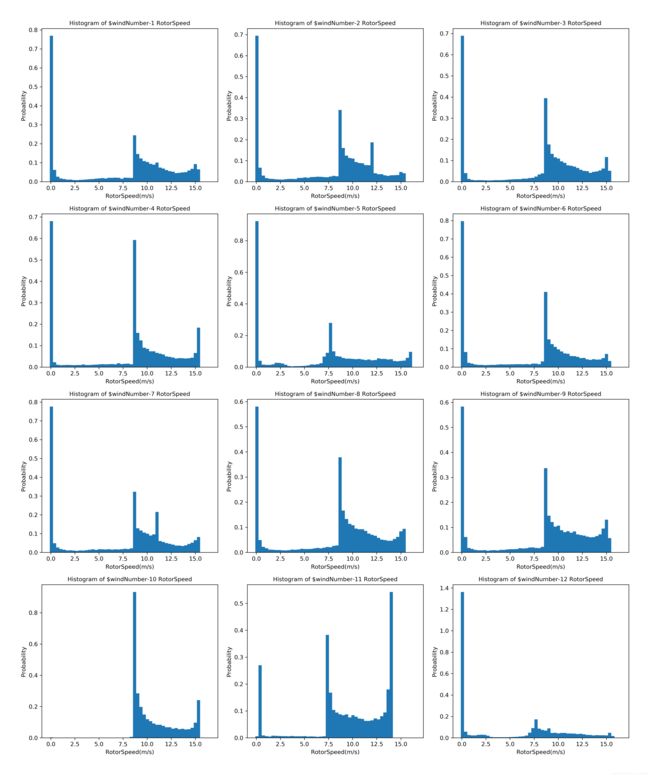
从图中可以看出除了10号风机，其他的风机转速为0的概率密度较高，特别是12号风机较为异常。风机转速主要集中于8-15之间，我们可以推测在此范围外的风机转速出现异常数据可能性较大。

3.风机功率密度直方图

plt.figure(figsize=(15,18))
font = {'weight':'normal','size':10}
for  i in list(range(1,13)):
    ax=plt.subplot(4,3,i)
    ax.hist(data.loc[data['WindNumber']==i,'Power'],range=(-110,2200.5),bins=50,density=True)
    plt.xlabel("Power(kw)",fontdict=font)
    plt.ylabel("Probability",fontdict=font)
    plt.title(r"Histogram of windNumber-%s Power"%i,fontdict=font)
    plt.tight_layout()
plt.savefig('./pic/Power_Histogram.png',bbox_inches='tight',pad_inches=0.5,dpi=300)

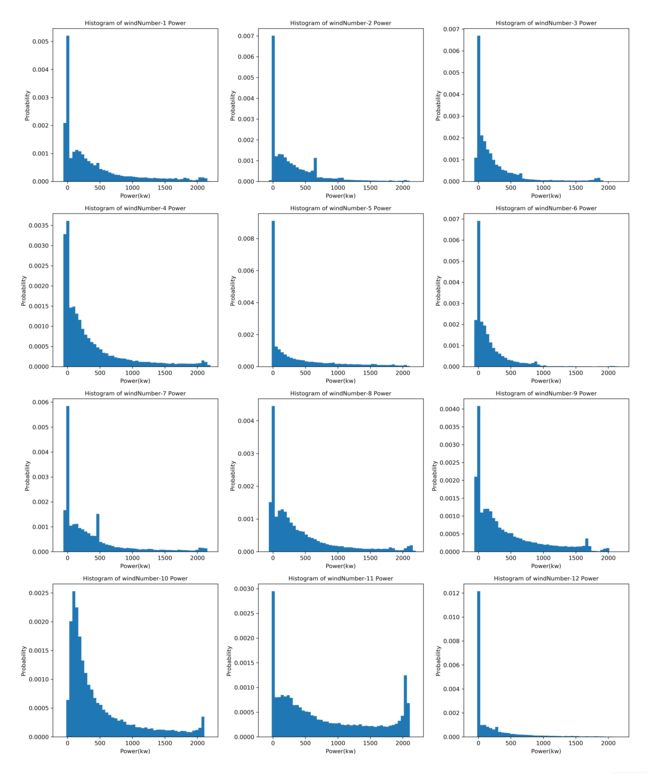
从图中可以看出，每台风机功率的分布并不是呈现正态分布，功率在0值附近概率分布较大。

（二）组合特征数据可视化

1.单位风速的功率和单位风机转速的功率散点图

f=plt.figure(figsize=(15,12))
font = {'weight':'normal','size':10}
for  i in list(range(1,13)):
    ax=plt.subplot(4,3,i)
    Y= data.loc[data['WindNumber']==i,'per_windspeed_power'] 
    X=data.loc[data['WindNumber']==i,'per_rotorspeed_power'] 
    plt.xlabel("Power of per WindSpeed",fontdict=font)
    plt.ylabel("Power of per RotorSpeed",fontdict=font)
    plt.title(r"scatter figure of  windNumber-%s"%i,fontdict=font)
    T = np.arctan2(Y,X) #for color  value
    plt.scatter(X,Y,s=55,c=T,alpha=0.5)
    if i in [5,10,11,12]:
        plt.xlim((-50,150))
        plt.ylim((-50,350))
    else:
        plt.xlim((-300,150))
        plt.ylim((-150,250))
    plt.tight_layout()
plt.savefig('./pic/per_Power.png',bbox_inches='tight',pad_inches=0.5,dpi=300)

从图中可以看出，1,2,3,4,6,7,8,9号风机有较多的功率为负值的情况（紫色区域）,猜测这些点可能都是异常数据。还有部分点明显偏离整体区域，如：风机11，12绿色区域的点，因此这些点也可以定义为异常值。

2.单位功率的风速和单位功率的风机转速散点图

f=plt.figure(figsize=(15,12))
font = {'weight':'normal','size':10}
plt.title(r"scatter of  windNumber-%s of windspeed and rotorspee of  per Power "%i,fontdict=font)
for  i in list(range(1,13)):
    ax=plt.subplot(4,3,i)
    Y= data.loc[(data['WindNumber']==i)&(data['Power']>=0),'per_power_windspeed'] 
    X=data.loc[(data['WindNumber']==i)&(data['Power']>=0),'per_power_rotorspeed'] 
    plt.title(r"scatter figure of  windNumber-%s"%i,fontdict=font)
    plt.xlabel("WindSpeed of per Power",fontdict=font)
    plt.ylabel("RotorSpeed of per Power",fontdict=font)
    T = np.arctan2(Y,X) #for color  value
    plt.scatter(X,Y,s=35,c=T,alpha=0.5)
    plt.tight_layout()

plt.savefig('./pic/windspeed_and_rotorspeed_per_Power.png',bbox_inches='tight',pad_inches=0.5,dpi=300)

正常情况下单位功率的风速和单位功率的风机转速都是在0值（非负）附近，但是由于个别值偏离，导致x,y轴坐标偏大，从图中可以很明显看出5,11,12号风机出现较多的单位功率的风速和单位功率的风机转速较大的情况，即功率较小或者为0，但是风速和转速较大或不为0。

当把X轴坐标取值范围定义为[0,0.5]，Y轴坐标取值范围定义为[0,0.2]，单位功率的风速和单位功率的风机转速散点图呈现正向线性关系。

五、基于规则筛选异常数据

基于以上分析及赛题对风机特征定义，本文给出几个基于规则定义异常数据标准：

• 风速、风机转速、功率其中任意一个小于等于0；
• 风速小于切入，功率大于0；
• 风速大于切除，功率大于0；
• 功率大于额定功率1.2倍；

这是赛题中

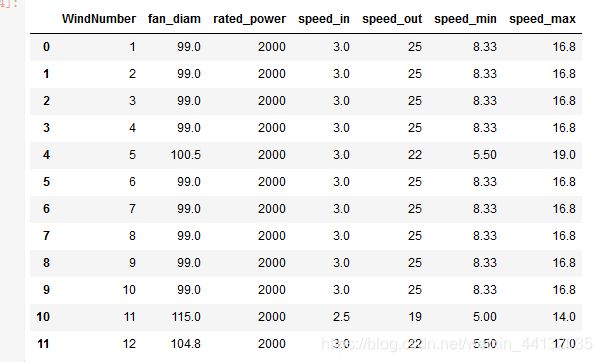
index_df = pd.read_excel('../data/index.xlsx', names=["WindNumber", "fan_diam", "rated_power",\
 "speed_in", "speed_out", "speed_min", "speed_max"])
index_df

data = data.merge(index_df, on='WindNumber')

基于自定义规则筛选异常值

data['label'] = 0
#异常值
#三列值小于0
data.loc[(data['WindSpeed'] <= 0) ,'label'] = 1
data.loc[(data['Power'] <=0    ) ,'label'] = 1
data.loc[(data['RotorSpeed'] <= 0),'label'] = 1
#风速小于切入，功率大于0
data.loc[(data['WindSpeed'] < data['speed_in'])  & (data['Power'] > 0 ) ,'label'] = 1
#风速大于切除，功率大于0
data.loc[(data['WindSpeed'] > data['speed_out']) & (data['Power'] > 0)  ,'label'] = 1
 
#功率大于额定功率1.2倍
data.loc[ data['Power'] > 1.2*data['rated_power'] ,'label'] = 1

基于规则，筛选的异常值在15以上，直接将其提交成绩在80左右。

六、基于聚类算法的异常数据筛选

这一部分主要是基于规则筛选异常值后，对于剩余样本值进一步通过聚类算法筛选，用到的聚类算法有，k-means，DBSCAN，IsolationForest、Gaussian distribution；

（一） k-means算法

import pandas as pd
from sklearn.cluster import KMeans,MiniBatchKMeans
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import silhouette_score
from sklearn.pipeline import Pipeline
from scipy.spatial.distance import cdist
from sklearn import metrics
import numpy as np

%matplotlib inline
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = [u'SimHei']  # 黑体 FangSong/KaiTi
mpl.rcParams['axes.unicode_minus'] = False

def kmeans_model(k,isStandard=True):
	"""
	定义kmeans的model 
	"""
    if isStandard:
        model = Pipeline([
        ('ss', StandardScaler()), #数据标准化过程
        ('kmeans', KMeans(n_clusters=k, init='k-means++',n_jobs=-1))])
    else:
          model = Pipeline([
        ('kmeans', KMeans(n_clusters=k, init='k-means++',n_jobs=-1))])
    return model



def evaluate(model,data,method='elbow'):
    """
    三种方法来评估肘部法则（MeanDistortions），轮廓系数（Silhouette），elbow方法
    """
    if method.lower() =='elbow':
        return model.score(data)
    
    elif method.lower() =='silhouette':
        return metrics.silhouette_score(data,model._final_estimator.labels_)
    
    else:
        return sum(np.min(
            cdist(data,model._final_estimator.cluster_centers_,
                 'euclidean'),axis=1))/data.shape[0]
    
### 筛选出最优的k（簇数）
features=['WindSpeed','Power','RotorSpeed']
data1=data[(data['WindNumber']==1)&(data['label']==0)][features]
K=range(2,22)
plt.figure(figsize=(15, 5), facecolor='#FFFFFF')
font = {'weight':'normal','size':14}
for index,method in enumerate(['elbow','silhouette','MeanDistortions']):
    ax=plt.subplot(1,3,index+1)
    scores=[]
    for k in K:
        model=kmeans_model(k,isStandard=True)
        model.fit(data1)
        score = evaluate(model,data1,method=method)
        scores.append(score)
    plt.plot(K,scores,'bx-')
    plt.xlabel('k',fontdict=font)
    plt.ylabel(u'%s scores'%method,fontdict=font)
plt.tight_layout(2.5)
plt.subplots_adjust(top=0.92)
plt.suptitle(u'k-means evaluate score', fontsize=18)

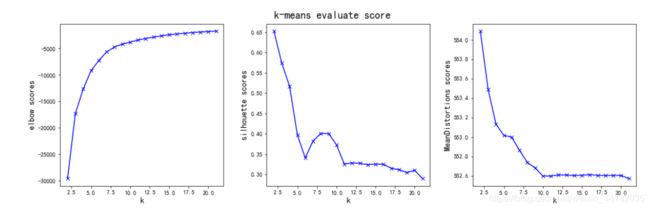为了找出合理的距离中心数，我们尝试尽可能多的聚类中心数（从1个到20个聚类中心），然后我们画出多种评估方法曲线，通过观察我们发现当我们的聚类中心数量增加到10个以上时三种评估方法曲线趋于收敛，因此我们大致可以将聚类中心数定为10.

# 计算每个数据点到其聚类中心的距离
from sklearn.preprocessing import StandardScaler
def getDistanceByPoint(df1, model):
    ss = StandardScaler()
    nd=ss.fit_transform(df1)
    distance = []
    for i in range(0,len(df1)):
        Xa = np.array(nd[i,:])
        Xb = model._final_estimator.cluster_centers_[model._final_estimator.labels_[i]]
        distance.append(np.linalg.norm(Xa-Xb))
    return pd.Series(distance)

##针对每一类机组做10个簇聚类模型，设定阈值，筛选出每一类的阈值之外样本作为异常值。
for num in WindNumberList:
    df1 = data[(data['WindNumber']==num)&(data['label']==0)][features].copy()
    model = kmeans_model(k=10)
    #设置异常值比例
    #df1 = df1.reset_index(drop=True)
    model.fit(df1)
    outliers_fraction = 0.1
    # 得到每个点到取聚类中心的距离，我们设置了10个聚类中心，kmeans[9]表示有10个聚类中心的模型
    distance = getDistanceByPoint(df1, model)
    #根据异常值比例outliers_fraction计算异常值的数量
    number_of_outliers = int(outliers_fraction*len(distance))
    #设定异常值的阈值
    threshold = distance.nlargest(number_of_outliers).min()
    #根据阈值来判断是否为异常值
    distace =list((distance >= threshold).astype(int))
    df1['label'] = distace
    data.iloc[df1[df1['label']==1].index,5] = 1

根据文献资料，风机的功率和风速是呈现函数关系，因此这里我们做了一个功率和风速的散点图，图中红色点标记为异常点，一些离群的样本被筛选出来，最后综合得分在0.87左右，因此模型达到预期提升效果。但是k-means模型任然有很多不足地方，例如设计阈值，聚类簇数以及聚类中心处置的选择等，都是一些超参数，直接影响模型聚类效果。

（二） DBSCAN算法

DBSCAN（Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法。 该算法将具有足够密度的区域划分为簇，并在具有噪声的空间数据库中发现任意形状的簇，它将簇定义为密度相连的点的最大集合。

形象来说，我们可以认为这是系统在众多样本点中随机选中一个，围绕这个被选中的样本点画一个圆，规定这个圆的半径以及圆内最少包含的样本点，如果在指定半径内有足够多的样本点在内，那么这个圆圈的圆心就转移到这个内部样本点，继续去圈附近其它的样本点，类似传销一样，继续去发展下线。等到这个滚来滚去的圈发现所圈住的样本点数量少于预先指定的值，就停止了。那么我们称最开始那个点为核心点，如A，停下来的那个点为边界点，如B、C，没得滚的那个点为离群点，如N

def dbscn_model(df,standar=True,eps=10, min_samples=2):
"dbscan模型的算法"
    if standar:
        model = Pipeline([
        ('ss', StandardScaler()), #数据标准化过程
        ('dbscan', DBSCAN(eps=eps, min_samples=min_samples))])
    else:
          model = Pipeline([
        ('dbscan', DBSCAN(eps=eps, min_samples=min_samples))])
    model.fit(df)
    return model


new_data=pd.DataFrame()
new_data=new_data.append(data[data['label']==1])
features=['WindSpeed','Power']

for num in WindNumberList:
    df1 = data[(data['WindNumber']==num)&(data['label']==0)].copy()
	##min_samples最小样本点个数，eps核心区域半径
    dbscan = dbscn_model(df1[features],standar=True,eps=0.15,min_samples=7) 
    label = list(dbscan._final_estimator.labels_)
    modeNumber = stats.mode(label)[0][0]
    newLabelList =[]
    if modeNumber !=0:
        print("风机%s-【%s】"%(num,modeNumber))
        ##筛选出聚类后少数样本群体作为异常点
        for i in label:
            if i==modeNumber:
                newLabelList.append(0)
            elif i==0:
                newLabelList.append(modeNumber)
            else:
                newLabelList.append(i)
    else:
        newLabelList.extend(label)
    df1['label'] = newLabelList
    new_data=new_data.append(df1)
    print("风机%s利用DBSCAN算法筛选后异常值数量【%s】"%(num,len(df1[df1['label']!=0])))
new_data = new_data.sort_values(['WindNumber','Time']).reset_index(drop=True)
new_data.loc[new_data['label']!=0,'label']=1
    

基于dbscan算法筛选异常值，模型综合得分和kmeans差不多，同样DBSCAN聚类算法也是超参数（min_samples最小样本点个数，eps核心区域半径）比较难以控制，并且DBSCAN适合于那些小规模异常点的识别。

（三） 孤立森林(IsolationForest)异常检测

IsolationForest算法它是一种集成算法(类似于随机森林)主要用于挖掘异常(Anomaly)数据，或者说离群点挖掘，总之是在一大堆数据中，找出与其它数据的规律不太符合的数据。该算法不采样任何基于聚类或距离的方法，因此他和那些基于距离的的异常值检测算法有着根本上的不同，孤立森林认定异常值的原则是异常值是少数的和不同的数据。它通常用于网络安全中的攻击检测和流量异常等分析，金融机构则用于挖掘出欺诈行为。

●当我们使用IsolationForest算法时需要设置一个异常值比例的参数contamination， 该参数的作用类似于之前的outliers_fraction。
  ●使用 fit 方法对孤立森林模型进行训练
  ●使用 predict 方法去发现数据中的异常值。返回1表示正常值，-1表示异常值。

def isolationForest_model(contamination='auto',max_samples=0.1,isStandard=True):
    if isStandard:
        model = Pipeline([
        ('ss', StandardScaler()), #数据标准化过程
        ('iForest', IsolationForest(max_samples=max_samples,contamination=contamination))])
    else:
          model = Pipeline([
        ('iForest', IsolationForest(max_samples=max_samples,contamination=contamination))])
    return model

features=['WindSpeed','Power', 'RotorSpeed']
new_data=pd.DataFrame()
new_data=new_data.append(data[data['label']==1])
WindNumberList = list(data['WindNumber'].unique())


for num in WindNumberList:
    df1 = data[(data['WindNumber']==num)&(data['label']==0)].copy()
    model = isolationForest_model(isStandard=True,contamination=0.05)
    model.fit(df1[features])
    #返回1表示正常值，-1表示异常值
    result = model.predict(df1[features])
    df1['label'] = result
    df1['label']=df1['label'].map({-1:1,1:0})
    new_data=new_data.append(df1)
    print("机组-【%s】，总数据量-【%s】，异常数据量-【%s】"%(num,len(df1),len(df1[df1['label']!=0])))
new_data = new_data.sort_values(['WindNumber','Time']).reset_index(drop=True)
new_data.loc[new_data['label']!=0,'label']=1

基于dbscan算法筛选异常值，其综合得分0.84，并没有实现预期显著提高，其主要原因是孤立森林算法的理论基础需要满足以下两点基础：

• （1）异常数据占总样本量的比例很小；
• （2）异常点的特征值与正常点的差异很大。

（四）基于高斯概分布的异常检测

高斯分布也称为正态分布。 它可以被用来进行异常值检测，不过我们首先要假设我们的数据是正态分布的。 不过这个假设不能适应于所有数据集。但如果我们做了这种假设那么它将会有一种有效的方法来发现异常值。

多元正态分布密度函数

Scikit-Learn的EllipticEnvelope模型，它在假设我们的数据是多元高斯分布的基础上计算出高斯分布的一些关键参数过程。过程大致如下:
  ●在排除规则定义异常数据之外的剩余数据集应用EllipticEnvelope（高斯分布）。
  ●我们设置contamination参数，它表示我们数据集中异常值的比例。
  ●使用decision_function来计算给定数据的决策函数。 它等于移位的马氏距离(Mahalanobis distances)。 异常值的阈值为0，这确保了与其他异常值检测算法的兼容性。
  ●使用predict 来预测数据是否为异常值(1 正常值, -1 异常值)

#针对机组1特征做高斯模型（手写算法模型）
import numpy as np 
import matplotlib.pyplot as plt 
import scipy.io as sio
import pandas as pd

#获取训练集中的均值和方差
def estimateGaussian(X,isCovariance):
    
    X_mean = np.mean(X,axis=0)  # (1,2),按列求均值
    if isCovariance:  #(多元高斯分布)
        sigma = (X-X_mean).T @ (X-X_mean) / len(X)  #(2,2)
    else:  #(原始高斯分布)
        sigma = np.var(X,axis=0)  #(1,2)求方差，按列
    return X_mean,sigma

#高斯分布函数
def gaussian(X,means,sigma):
    
    if np.ndim(sigma) == 1:  #np.ndim判断矩阵为几维。向量为一维，矩阵为二维，若有3个[]，即为3维
        sigma = np.diag(sigma)  #若为一维，则生成一个以一维数组为对角线元素的矩阵；二维则输出对角线元素
    n = X.shape[1]
    first = np.power(2*np.pi,-n/2) * (np.linalg.det(sigma)**(-0.5))  #np.linalg.det求矩阵的行列式，**的意思是次方
    second = np.diag((X-means)@(np.linalg.inv(sigma))@(X-means).T)
#     print(second)
    P = first * np.exp(-0.5*second)
    P = P.reshape((-1,1))   #(任意行，1)
    return P   #(307,1)

#画等高线
def plotGaussian(X,means,sigma):
    
    x = np.arange(-1, 3.5, 0.1) 
    y = np.arange(-1, 3.5, 0.1)
    xx, yy = np.meshgrid(x,y)  
    z= gaussian(np.c_[xx.flatten(),yy.flatten()], means, sigma)  # 计算对应的高斯分布函数
    zz = z.reshape(xx.shape)  
    plt.plot(X[:,0],X[:,1],'bx')
    plt.xlim((-1,3.5))
    plt.ylim((-1,3.5))
    contour_levels = [10**h for h in range(-20,0,3)]
    plt.contour(xx, yy, zz, contour_levels)


df1=data[(data['WindNumber']==1)&(data['label']==0)].copy()
features=['per_power_windspeed','per_power_rotorspeed']
means,sigma1 = estimateGaussian(df1[features].values,isCovariance = True)
plotGaussian(df1[features].values,means,sigma1)

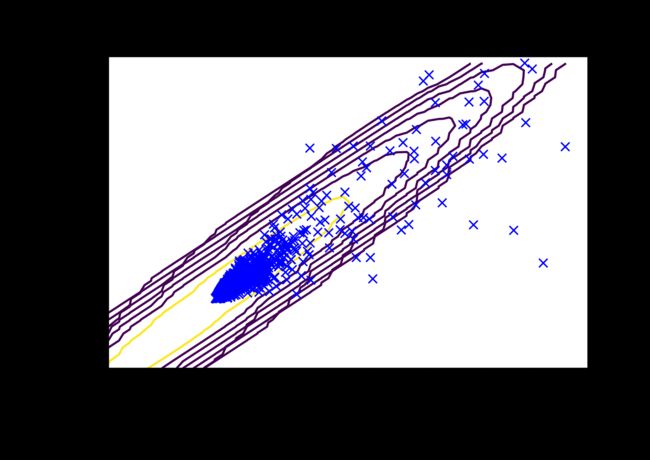
针对所有机组利用sklearn的API接口做高斯模型的的异常检测，代码如下：

from sklearn.covariance import EllipticEnvelope
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

def gaussian_model(contamination=0.05,standar=True):
    if standar:
        model = Pipeline([
        ('ss', StandardScaler()), #数据标准化过程
        ('gaussian', EllipticEnvelope(contamination=contamination))])
    else:
          model = Pipeline([
        ('gaussian', EllipticEnvelope(contamination=contamination))])
    return model


WindNumberList = list(data['WindNumber'].unique())
features=['per_power_windspeed','per_power_rotorspeed']
new_data=pd.DataFrame()
new_data=new_data.append(data[data['label']==1])


for num in WindNumberList:
    df1 = data[(data['WindNumber']==num)&(data['label']==0)].copy()
    model = gaussian_model(standar=True,contamination=0.05)
    model.fit(df1[features])
    #返回1表示正常值，-1表示异常值
    result = model.predict(df1[features])
    df1['label'] = result
    df1['label']=df1['label'].map({-1:1,1:0})
    new_data=new_data.append(df1)
    print("机组-【%s】，总数据量-【%s】，异常数据量-【%s】"%(num,len(df1),len(df1[df1['label']!=0])))

基于高斯概分布的异常检测，综合得分低于0.8，效果比基于规则的判断异常值更低，其主要原因在于’per_power_windspeed’和’per_power_rotorspeed’这两个特征并不是呈现多元正太分布，因此基于高斯概分布的异常检测的前提假设并不成立导致模型应用效果并不理想。

七、基于线性回归算法的异常数据筛选

我们可以基于线性模型拟合风速和功率，并计算预测值和真实值的误差值，设定阈值，确定风机数据是否异常。

import time
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')

from sklearn.linear_model import LinearRegression,RANSACRegressor
from sklearn.preprocessing import PolynomialFeatures,StandardScaler

def sample_data(data,i,scal):
    """
    按照排除规则按照分层取样
    """
    one=data[(data.WindNumber==i)&(data.label==0)]
    to_train_regression=one[(data.day<sup)&(data.day>inf)][data.Power<2000]
    to_train_regression['Power_n']=np.floor(to_train_regression.Power/scal)
    target_num = int(to_train_regression.groupby("Power_n")['Power_n'].count().quantile(0.4))
    sample_datas = []
    for pn in to_train_regression['Power_n'].unique().tolist():
        to_samp_data =to_train_regression[to_train_regression.Power_n==pn]
        al = to_samp_data['Power_n'].count()
        sample_data = to_samp_data.sample(n=min(target_num,al) )
        sample_datas.append(sample_data)
        
    return sample_datas


data['timeStamp'] = data.apply(lambda x:time.mktime(time.strptime(x['Time'],'%Y/%m/%d %H:%M')),axis=1 )
data['day'] = data.apply(lambda x: int(x['timeStamp'] /(3600*24)) ,axis=1 )


models= []
scal=10
max_=[20000,20000,17750,20000,18200,20000,20000,20000,20000,20000,20000,20000]
min_=[17780,17800,17650,18100,18100,17780,17800,17770,17770,18100,18100,18100]
for i in list(range(12)):
    sup = max_[i]
    inf = min_[i]
    i=i+1
    sample_datas = sample_data(data,i,sup,inf,scal)
    d = pd.concat(sample_datas)
    x=d[['Power']]
    y=d[['WindSpeed']]
    ## 使用RANSAC清除异常值高鲁棒对的线性回归模型
    poly_linear_model = RANSACRegressor(LinearRegression(),loss='squared_loss' )
    ## PolynomialFeatures 扩充特征
    poly_linear_model.fit(PolynomialFeatures(degree = 3).fit_transform(x), y) 
    models.append(poly_linear_model)

max_p=2000
resx = []
for i in list(range(12)):
    modle = models[i]
    i=i+1
    q1 = data[data.WindNumber==i]
    py=modle.predict(PolynomialFeatures(degree = 3).fit_transform(q1[['Power']]))
    q1['diffpWindSpeed']=(py-q1[['WindSpeed']])
    f=-1.1
    max_p =q1.Power.max()-150
    q1['ds']=q1.apply(lambda x:0 if ( (x['diffpWindSpeed'] > f and x['diffpWindSpeed'] <-f*1.5) or x['Power']>max_p )    else 1,axis=1)
    resx.append(q1)
r = pd.concat(resx)
r.sort_index()
data['ds']=r['ds']
data['diffpWindSpeed']= r['diffpWindSpeed']
data['label']=data.apply(lambda x: 1 if (x['label']==1 or  x['ds']==1 ) else 0 ,axis=1)

基于线性模型拟合风速和功率,计算风速预测值和真实值差值，设定阈值，达到清洗异常数据的目的，其综合得分在0.9以上。模型效果显著提高。从上图中风机10和风机7还有小部分数据偏离整体群体，因此可以DBSCAN算法识别这部分k离群点。其最终模型效果F1score可以达到0.93以上。最终清洗后，风机功率散点图如下：

结束语：，本次数据风机异常数据的清洗主要利用“规则+线性拟合+DBSCAN聚类算法”三种方式组合完成数据清洗。由于本赛题属于无监督学习，对于所应用模型超参数调节很难控制，只能根据每天三次提交获得分数估计超参数是否合适。后期可以针对前面扩充的特征作为自变量，和已经预测出的label做半监督学习分类模型训练，或许效果更好。