新型飞蛾火焰优化算法-附代码
新型飞蛾火焰优化算法
文章目录
- 新型飞蛾火焰优化算法
-
- 1.飞蛾扑火优化算法
- 2. 改进飞蛾扑火优化算法
-
- 2.1 Kent混沌搜索策略
- 2.2 动态惯性权值
- 3.实验结果
- 4.参考文献
- 5.Matlab代码
- 6.Python代码
摘要:飞蛾火焰优化算法(Moth-Flame Optimization,MFO)是一种自然激励且易于实现的全局优化算法,在许多实际优化任务中表现出良好的性能。然而,MFO算法存在早熟收敛和容易陷入局部最优解的问题,针对这些不足,提出了一种Kent混沌动态惯性权值的改善飞蛾火焰优化算法(Ameliorative MFO,AMFO)。在AMFO算法中,引入Kent混沌映射搜索策略帮助当前最优解跳出局部最优;采用基于适应度值和迭代次数的动态惯性权值策略来平衡算法的开发和探索能力,以进一步提升MFO算法性能。
1.飞蛾扑火优化算法
基础飞蛾扑火优化算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/107764895
2. 改进飞蛾扑火优化算法
2.1 Kent混沌搜索策略
Kent混沌映射模型描述如下:
Z i + 1 = { Z t / a , 0 < Z t ⩽ a ( 1 − Z t ) / ( 1 − a ) , a < Z t < 1 (7) Z^{i+1}=\left\{\begin{array}{l} Z^t / a, 0
式中, 控制参数 a ∈ ( 0 , 1 ) a \in(0,1) a∈(0,1), Kent 映射的 Lyapunov指数大 于 0 , 映射处于混沌状态。本文取 a = 0.4 a=0.4 a=0.4, 其概率密度 函数在 ( 0 , 1 ) (0,1) (0,1) 内服从均匀分布, 即 ρ ( Z ) = 1 \rho(Z)=1 ρ(Z)=1 。初始状态微 小不确定性的发散比率可以由 Lyapunov指数描述 [ 14 ] { }^{[14]} [14], 此 时 Kent混沌的 Lyapunov指数为 0.696 0.696 0.696, 大于经典 Logistic 的 0.691 0.691 0.691 。
在 MFO算法中, 假设经过连续 limit 次迭代搜索后 解没有得到明显改善, 表明这个解陷入局部最优, 因此 采用Kent对其进行混沌优化。对 MFO算法的当前最优 解进行混沌优化,优化问题的解空间为 [ X min , X max ] \left[X_{\min }, X_{\max }\right] [Xmin,Xmax], Kent混沌优化步骤如下:
(1)利用式 (8) 将当前最优解 M i M_i Mi 映射到 Kent方程 的定义域 [ 0 , 1 ] [0,1] [0,1] 内:
Z 0 = M i − M min M max − M min (8) Z^0=\frac{M_i-M_{\min }}{M_{\max }-M_{\min }} \tag{8} Z0=Mmax−MminMi−Mmin(8)
(2)生成混沌序列。用 Kent方程迭代产生 C max C_{\max } Cmax 个 混沌变量序列 Z k ( k = 1 , 2 , ⋯ , C max ) Z_k\left(k=1,2, \cdots, C_{\max }\right) Zk(k=1,2,⋯,Cmax);
(3) 利用载波操作先将 Z k Z_k Zk 放大, 然后再加载到待搜 索的个体 M i M_i Mi 上, 从而得到混沌算子操作后的原解空间 的领域内的新的个体位置 U k U_k Uk, 其中 k = 1 , 2 , ⋯ , C max k=1,2, \cdots, C_{\max } k=1,2,⋯,Cmax :
U k = M i + M max − M min 2 × ( 2 Z k − 1 ) (9) U_k=M_i+\frac{M_{\max }-M_{\min }}{2} \times\left(2 Z_k-1\right) \tag{9} Uk=Mi+2Mmax−Mmin×(2Zk−1)(9)
(4) 计算 U k U_k Uk 的适应度值 f ( U k ) f\left(U_k\right) f(Uk), 并与 M i M_i Mi 的适应度 值比较,保留最好解。
2.2 动态惯性权值
惯性权值参数对算法的全局和局部搜索有着重要影响。MFO算法中权值大小决定了上次迭代中火焰个体对本次迭代中飞蛾个体的影响程度。迭代初期,希望有较高的全局搜索能力以探索新的解空间,跳出局部极值;迭代后期,则重视局部开发以加快收敛并发现精确解。若MFO算法采用线性递减惯性权值,对于复杂高维函数, 当迭代次数较大时, 每次迭代的惯性权值的变 化量较小,将影响权值调整策略功能的发挥; 同时,单一 的变化模式, 在迭代后期, 飞蛾在陷入局部最优后将很 难飞出。基于上述分析,除了考虑算法所处的迭代阶段 以外, 还应该将飞蛾的适应度值考虑进去, 即权值大小 由迭代次数和飞蛾的适应度值共同决定。动态惯性权 值 w w w 描述如下:
w i , j = exp ( f ( j ) / μ ) 2.4 + ( exp ( − f ( j ) / μ ) ) iter (10) w_{i, j}=\frac{\exp (f(j) / \mu)}{2.4+(\exp (-f(j) / \mu))^{\text {iter }}} \tag{10} wi,j=2.4+(exp(−f(j)/μ))iter exp(f(j)/μ)(10)
式中, μ \mu μ 为第一次寻优过程的平均适应度值; f ( j ) f(j) f(j) 为第 j j j 个飞蛾的适应度值; iter 表示当前迭代次数。针对极 小值优化问题, 设置飞蛾优化解对应的函数值为适应度 值, 随着迭代次数增加, f ( j ) f(j) f(j) 呈现非线性减小趋势, 2.4 + ( exp ( − f ( j ) / μ ) ) iter 2.4+(\exp (-f(j) / \mu))^{\text {iter }} 2.4+(exp(−f(j)/μ))iter 呈现非线性增加趋势, 故权值 w w w 随 着适应度值和迭代次数呈现非线性减小趋势。改进后的位置更新公式如式(11)所示:
S ( M i , F j ) = w i , j × D i × e b t × cos ( 2 π t ) + ( 1 − w i , j ) × F j ( 11 ) S\left(M_i, F_j\right)=w_{i, j} \times D_i \times \mathrm{e}^{b t} \times \cos (2 \pi t)+\left(1-w_{i, j}\right) \times F_j(11) S(Mi,Fj)=wi,j×Di×ebt×cos(2πt)+(1−wi,j)×Fj(11)
动态惯性权值随着迭代次数和适应度值非线性动 态变化, 人工飞蛾逐渐向适应度值较优的火焰运动, 利 于 MFO算法的性能提升。
基于上述描述,AMFO算法流程描述如下:
(1) 初始化算法参数: 飞蛾数量 n n n 、维数 d d d 、最大迭 代次数 T T T 等;
(2)种群初始化, 按式 (1) 格式初始化种群;
(3)计算种群中人工飞蛾和人工火焰的适应度值, 并按适应度值排序;
(4) 按照 3.1 3.1 3.1 节内容更新第一个火焰 F 1 F_1 F1 (当前为止 最优解);
(5)利用式(6) 更新火焰数量;
(6) 按式 (10) 更新动态惯性权值;
(7)计算 D i = ∣ F j − M i ∣ D_i=\left|F_j-M_i\right| Di=∣Fj−Mi∣, 按式(11) 更新飞蛾位置;
(8) 若满足终止条件, 算法结束, 获得最优解, 否则 返回步骤(3)。
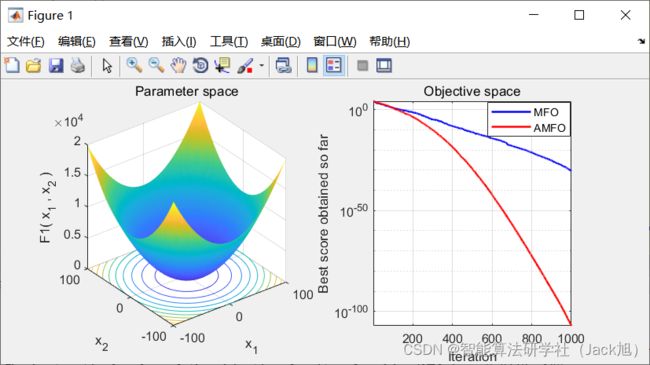
3.实验结果
4.参考文献
[1]田鸿,陈国彬,刘超.新型飞蛾火焰优化算法的研究[J].计算机工程与应用,2019,55(16):138-143.