Python：自适应滤波器简介及其实现方法

• 实现自适应滤波器的 ✨ 最多的两个 Github 仓库：
  • ✨ 回声消除自适应滤波器设计包：ewan-xu/pyaec: simple and efficient python implemention of a series of adaptive filters. including time domain adaptive filters(lms、nlms、rls、ap、kalman)、nonlinear adaptive filters(volterra filter、functional link adaptive filters)、frequency domain adaptive filters(frequency domain adaptive filter、frequency domain kalman filter) for acoustic echo cancellation.
  • 另一个自适应滤波器（该包实现的自适应滤波器比较少，但是说明详细）：Wramberg/adaptfilt: Adaptive filtering module for Python

✨ 注意：我写这篇博客的目的是学习，如果真感兴趣可以参考文章最后的参考文献1¹（大神写的）。

一、自适应滤波器简介

1.1 自适应滤波器原理、特点、分类及其作用

自适应滤波器是利用前一时刻滤波器参数，自动调整当前时刻滤波器参数，以适应信号随时间变化的统计特征，从而实现最优滤波，其原理如下图所示：

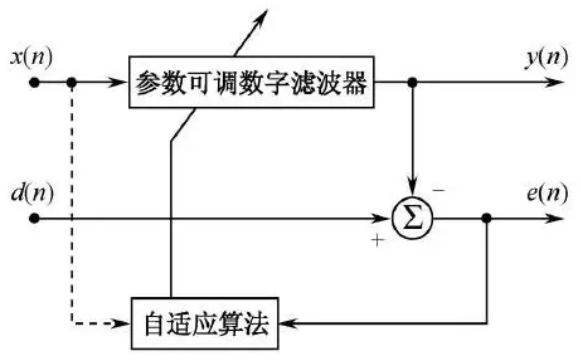
• $x(n)$为输入信号；
• $d(n)$为期望信号；
• $y(n)$为输入信号通过参数可调数字滤波器（自适应滤波器）的输出信号；
• $e(n)$为误差信号。

自适应滤波器的原理如下所示：

• 输入信号$x(n)$通过参数通过自适应滤波器(Adaptive Filter)后产生输出信号$y(n)$，将其与期望信号$d(n)$进行比较，形成误差信号$e(n)$，通过自适应算法对滤波器参数进行调节，最终使$e(n)$的均方值最小。
• 自适应滤波可以利用前一时刻已知滤波器参数的结果，自动调节当前时刻的滤波器参数，以适应信号随时间变化的统计特性，从而实现最优滤波。

自适应滤波器的特点：
（1）无需提取信息的先验统计特性；
（2）直接利用观测数据，并依据某种判据在观测过程中不断递归更新；
（3）最优化。

自适应滤波器的分类：
（1）按结构分类：横向结构、格型结构；
（2）按算法分类：随机梯度、最小二乘法；
（3）按处理方式分类：成批处理、递归处理。

常用的两类自适应滤波器包括维纳滤波器与卡尔曼滤波器：

• 维纳滤波器： 其参数是固定的，适用于平稳随机过程；
• 卡尔曼滤波器： 其参数时变的，适用于非平稳过程。

• 自适应滤波器的作用：
  自适应滤波器是应用于未知信号的滤波器，在实际应用中，困难在于信号模型是未知的，所以自适应滤波器的关键是寻找一种算法，使系数能以满足实际需求的精度与速度趋近于分段近似平稳滤波器的稳态权系数。

1.2 自适应滤波器的数学表示方法²

自适应滤波器的详细模型如下图（图片来源）所示：

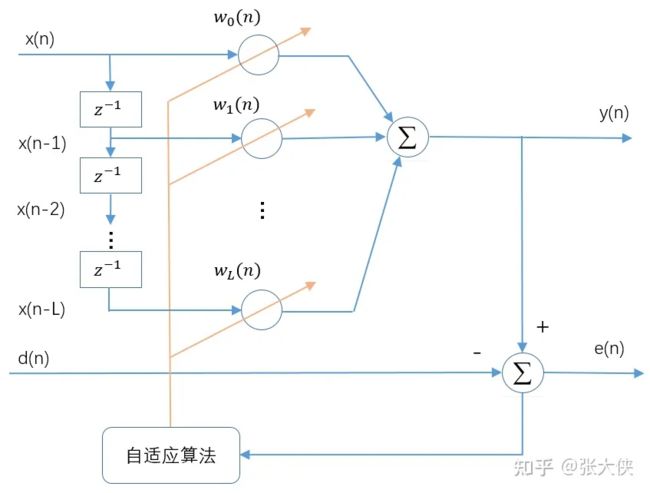
输入信号：
$$\mathbf{x}(n)=[x(n),x(n-1),...,x(n-L){]}^T$$

输出信号：
$$\mathbf{y}(n)=\sum _{k=0}^L{w}_k(n)x(n-k)$$

自适应线性组合器的$L+1$个权系数构成一个权重系数适量，称为权重适量，用$\mathbf{w}(n)$表示：
$$\mathbf{w}=[w_0(n),w_1(n),...,w_L(n){]}^T$$

因此，$y(n)$可以表示为：
$$\mathbf{y}(n)={\mathbf{x}}^T(n)\mathbf{w}(n)={\mathbf{w}}^T(n)\mathbf{x}(n)$$

误差信号为：
$$e(n)=d(n)-y(n)=d(n)-x^T(n)w(n)=d(n)-{\mathbf{w}}^T(n)\mathbf{x}(n)$$

自适应线性组合器采用误差信号$e(n)$均方值最小的准则，即：
$$\begin{gathered} \xi (n)=E[e^2(n)]=E[d^2(n)]+{\mathbf{w}}^T(n)E[\mathbf{x}(n){\mathbf{x}}^T(n)]\mathbf{w}(n) \\ -2E[d(n){\mathbf{x}}^T(n)]\mathbf{w}(n) \end{gathered}$$

输入信号$\mathbf{x}(n)$的自相关矩阵$\mathbf{R}$为：
$$\begin{array}{rl}\mathbf{R}& =E[\mathbf{x}(n){\mathbf{x}}^T(n)]\\ & =\left[\begin{array}{c}E[x(n)x(n)],E[x(n)x(n-1)],...,E[x(n)x(n-L)]\\ E[x(n-1)x(n)],E[x(n-1)x(n-1)],...,E[x(n-1)x(n-L)]\\ ⋮\\ E[x(n-L)x(n)],E[x(n-L)x(n-1)],...,E[x(n-L)x(n-L)]\end{array}\right]\end{array}$$

期望信号$d(n)$与输入信号$\mathbf{x}(n)$的互相关矩阵$\mathbf{P}$为：
$$\begin{array}{rl}\mathbf{P}& =E[d(n)\mathbf{x}(n)]\\ & =E[d(n)x(n),d(n)x(n-1),...,d(n)x(n-L)]\end{array}$$

将自相关矩阵$\mathbf{R}$与互相关矩阵$\mathbf{P}$带入$\xi$，得到均方误差的简单表达形式：
$$\xi (n)=E[d^2(n)]+{\mathbf{w}}^T\mathbf{R}\mathbf{w}-2{\mathbf{P}}^T\mathbf{w}$$

由上式可以得出，在输入信号与参考响应都是平稳随机信号的前提下，均方误差是权重适量的各分量的二次函数。该函图像是一个$L+2$维空间中那个一个中间下凹的超抛物面，有唯一的最低点，该曲面称为均方误差性能曲面，简称性能曲面。

均方误差性能曲面$\xi$的梯度为：
$$\nabla =\frac{\partial \xi }{\partial w}=2\mathbf{R}\mathbf{w}-2\mathbf{P}$$
另，$\nabla =0$，可以得到最小均方误差对应而最优权重适量${\mathbf{W}}^{\ast }$（也称为维纳解），即${\mathbf{w}}^{\ast }={\mathbf{R}}^{-1}\mathbf{P}$。

虽然维纳解的表达式我们可以通过上面的数学推导得到，但是在实际应用存在如下问题：

• 需要知道自相关矩阵$\mathbf{R}$与互相关矩阵$\mathbf{P}$，但是由于输入信号$\mathbf{x}(n)$是不确定的，所以无从获得$\mathbf{R}$与$\mathbf{P}$；
• 矩阵的逆计算量大：$O(n^3)$；
• 如果信号非平稳，则$\mathbf{R}$与$\mathbf{P}$每次都不一样，需要重复计算。

这也是为什么要设计不同的自适应滤波器算法的原因。

二、不同类型自适应滤波器的代码实现³

对于自适应滤波器的算法可以分为时域与频域两类，本文展示如下两类自适应滤波器：

• 时域自适应滤波器：LMS、NLMS、RLS
• 频域自适应滤波器：NLMS

2.1 时域自适应滤波器算法的实现

2.1.1 LMS自适应滤波器算法的实现

LMS自适滤波器算法流程为：

$$\begin{array}{rl}& \mathbf{y}(n)={\mathbf{w}}^T(n)\mathbf{x}(x)\\ & \mathbf{e}(n)=d(n)-y(n)\\ & \mathbf{w}(n+1)=\mathbf{w}(n)+2\mu e(n)\mathbf{x}(n)\end{array}$$

LMS自适滤波器实现代码如下所示：

import numpy as np

def lms(x, d, N=4, mu=0.1):
    """LMS (Least Mean Squares) 滤波器

    Args:
        x (_type_): 输入信号
        d (_type_): 期望信号
        N (int, optional): (个人理解)滤波器长度. Defaults to 4.
        mu (float, optional): 迭代步长. Defaults to 0.1.
    返回值:
        e (_type_): 误差信号
    """
    # LMS迭代步数
    n_Iters = min(len(x), len(d)) - N
    u = np.zeros(N)     # 每次输入自适应滤波器的信号
    w = np.zeros(N)     # 滤波器权重系数
    e = np.zeros(n_Iters)   # 误差信号
    for n in range(n_Iters):
        # 下面两条指令将输入信号 u 转换为
        # [当前信号, 前一个信号, 前两个信号, ..., 前N-1个信号]的格式
        u[1:] = u[:-1]
        u[0] = x[n]

        # 根据LMS方法计算每次迭代的误差信号
        e_n = d[n] - np.dot(u, x)

        # 根据当前误差e、步长u、输入信号u更新滤波器权重w
        w = w + mu * e_n * u

        # 存储每次迭代误差e_n到误差向量e中
        e[n] = e_n
    return e

LMS的优点： 算法简单易于实现，算法复杂度低，能够抑制旁瓣效应。
LMS的缺点：

• (1) 收敛速度慢，由于LMS滤波器系数更新都是逐点进行的，每次采样点梯度估计对句真实梯度存在误差，导致滤波器系数的每次更新不会按照真实的梯度方向更新，从而导致收敛速度慢。
  (2) 跟踪性能较差，并且随着滤波器阶数(步长参数)升高，系统的稳定性下降
  (3) LMS要求不同时刻的输入向量$x(n)$线性无关（LMS的独立性假设）。如果输入信号存在相关性，会导致前一次迭代产生的梯度噪声传播到下一次迭代，从而导致误差的反向传播，收敛速度变慢，跟踪性能差。

2.2.2 NLMS自适应滤波器算法的实现

• NLMS自适应滤波器算法对LMS算法输入信号做了归一化处理，并且可以采用变步长因子。与LMS相比，其收敛速度更快，而且计算量与LMS相当。

NLMS自适应滤波器算法流程为：

$$\begin{array}{rl}& \mathbf{y}(n)={\mathbf{w}}^T(n)\mathbf{x}(x)\\ & \mathbf{e}(n)=d(n)-y(n)\\ & \mathbf{w}(n+1)=\mathbf{w}(n)+\frac{\mu e(n)\mathbf{x}(n)}{{\mathbf{x}}^H(n)\mathbf{x}(n)}\end{array}$$

NLMS自适应滤波器的实现代码如下所示：

import numpy as np

def nlms(x, d, N=4, mu=0.1):
    """NLMS (Normalized Least Mean Squares) 滤波器

    Args:
        x (_type_): 输入信号
        d (_type_): 期望信号
        N (int, optional): (个人理解)滤波器长度. Defaults to 4.
        mu (float, optional): 迭代步长. Defaults to 0.1.
    返回值:
        e (_type_): 误差信号
    """
    # NLMS迭代步数
    n_Iters = min(len(x), len(d)) - N
    u = np.zeros(N)     # 每次输入自适应滤波器的信号
    w = np.zeros(N)     # 滤波器权重系数
    e = np.zeros(n_Iters)   # 误差信号
    for n in range(n_Iters):
        # 下面两条指令将输入信号 u 转换为
        # [当前信号, 前一个信号, 前两个信号, ..., 前N-1个信号]的格式
        u[1:] = u[:-1]
        u[0] = x[n]

        # 根据LMS方法计算每次迭代的误差信号
        e_n = d[n] - np.dot(u, x)

        # 根据当前误差e、步长u、输入信号u更新滤波器权重w
        w = w + mu * e_n * u / (np.dot(u, u) + 1e-3)

        # 存储每次迭代误差e_n到误差向量e中
        e[n] = e_n
    return e

2.3.3 RLS自适应滤波器算法的实现

• RLS (Recursive Least Square) 算法为递归最小二乘法，是最小二乘法的一类快速算法，递归最小二乘自适应滤波器相对于LMS自适应滤波器横向滤波器具有更好的性能。

RLS与LMS相比，RLS最大的缺点是计算量较大，但是其收敛速度非常快。当环境噪声为平稳随机信号时，LMS算法效果明显，但当环境噪声为非平稳随机噪声时，LMS算法难以自适应跟踪统计特性不断变化的外界噪声，收敛效果一般。RLS算法能够该缺点，在非平稳的环境下获得满意的效果。

一个$p$-th阶的RLS自适应滤波器的算法步骤如下所示：

• 参数：

$$\begin{array}{rl}& \mathbf{p}=\text{filter order}\\ & \mathbf{\lambda }=\text{forgetting factor}\\ & \mathbf{\delta }=\text{value to initialize P(0)}\end{array}$$

• 初始化：

$$\begin{array}{rl}& \mathbf{w}(n)=0\\ & x(k)=0,k=-p,...,-1,\\ & d(k)=0,k=-p,...,-1\\ & \mathbf{P}(0)=\delta \mathbf{I},\text{where }\mathbf{I}\text{is the identity matrix of rank}p+1\end{array}$$

• 对于$n=1,2,...$执行如下计算过程：
  $$\begin{array}{rl}& \mathbf{x}(n)=\left[\begin{array}{c}x(n)\\ x(n-1)\\ ⋮\\ x(n-p)\end{array}\right]\\ & e(n)=d(n)-{\mathbf{x}}^T(n)\mathbf{w}(n-1),\\ & \mathbf{g}(n)=\mathbf{P}(n-1)\mathbf{x}(n)\{\lambda +{\mathbf{x}}^T(n)\mathbf{P}(n-1)\mathbf{x}(n){\}}^{-1}\\ & \mathbf{P}(n)={\lambda }^{-1}\mathbf{P}(n-1)-\mathbf{g}(n){\mathbf{x}}^T(n){\lambda }^{-1}\mathbf{P}(n-1)\\ & \mathbf{w}(n)=\mathbf{w}(n-1)+e(n)\mathbf{g}(n)\end{array}$$

RLS自适应滤波器的实现代码如下所示：

import numpy as np

def rls(x, d, N=4, lmbd=0.999, delta=0.01):
    """RLS (Recursive Least Squares) 滤波器

    Args:
        x (_type_): 输入信号
        d (_type_): 期望信号
        N (int, optional): 滤波器长度. Defaults to 4.
        lmbd (float, optional): 遗忘因子 (Forgetting Factor). Defaults to 0.999.
        delta (float, optional): 初始化 P[0] 的单位矩阵. Defaults to 0.01.

    返回值:
        e (_type_): 误差信号
    """
    # RLS迭代步数
    n_Iters = min(len(x), len(d)) - N
    lmbd_inv = 1/ lmbd  # 遗忘因子的倒数
    u = np.zeros(N)     # 每次输入自适应滤波器的信号
    w = np.zeros(N)     # 滤波器权重系数
    P = np.eye(N) * delta   # 目前不清楚其具体内涵，将其理解为当成中算法间变量
    e = np.zeros(n_Iters)   # 误差信号
    for n in range(n_Iters):
        # 下面两条指令将输入信号 u 转换为
        # [当前信号, 前一个信号, 前两个信号, ..., 前N-1个信号]的格式
        u[1:] = u[:-1]
        u[0] = x[n]

        # 计算每次迭代的误差信号
        e_n = d[n] - np.dot(u, x)

        # 计算上面RLS算法中的g(n)
        r = np.dot(P, u)
        g = r / (lmbd + np.dot(u, r))

        # 更新滤波器参数w与P
        w = w + e_n * g
        P = lmbd_inv * (P - np.outer(g, np.dot(u, P)))

        # 存储每次迭代误差e_n到误差向量e中
        e[n] = e_n
    return e

2.2 频域自适应滤波器NLMS算法的实现

上面的三种自适应滤波器都是在时域中实现的，我们还可以通过通过OLS (Ordinary Least Square) 进行分段FFT计算卷积，以实现在频域中实现自适应滤波器。下面以NLMS算法为出发点，实现一种 Block NLMS 自适应滤波器，其算法流程如下所示：

$$\begin{array}{rl}& u_{B,n}=\text{col}u(nB+B-1),...,u(nB+1),u(nB)\\ & u_{2B,n}^{\prime }=F\left[\begin{array}{c}{u}_{B,n}\\ u_{B,n-1}\end{array}\right]\triangleq \text{clo}\{u_k^{\prime }(n),k=0,1,...,2B-1\}\\ & \\ & \\ & {\lambda }_k(n)=\beta {\lambda }_k(n-1)+(1-\beta )|u_k^{\prime }(n){|}^2,k=0,1,...,2B-1\\ & u_{k,n}^{\prime }=[u_k^{\prime }(n)\dots u_k^{\prime }(n-\frac{M}{B}+1)],k=0,1,...,2B-1\\ & y_k^{\prime }(n)=u_{k,n}^{\prime }{l}_{k,n-1}^{\prime },k=0,1,...,2B-1\\ & \\ & {\hat{d}}_{B,n}=\left[{\mathbf{I}}_B{0}_{B\times B}\right]F^{\ast }\text{col}\{y_0^{\prime }(n),...,y_{2B-1}^{\prime }(n)\}\\ & e_{B,n}=d_{B,n}-{\hat{d}}_{B,n}\\ & e_{2B,n}^{\prime }=F\left[\begin{array}{c}{\mathbf{I}}_B\\ 0_{B\times B}\end{array}\right]e_{B,n}\triangleq \text{col}\{e_k^{\prime }(n),k=0,1,...,2B-1\}\\ & \\ & l_{k,n}=l_{k,n-1}+\frac{\mu }{{\lambda }_k(n)}{u}_{k,n}^{\prime \ast }{d}_k(n{)}^{\prime },k=0,1,...,2B-1\\ & \left[\begin{array}{c}{l}_{0,n}^{c⊺}\\ l_{1,n}^{c⊺}\\ ⋮\\ l_{2B-1,n}^{c⊺}\end{array}\right]=\frac{1}{2B}{F}^{\ast }\left[\begin{array}{cc}{\mathbf{I}}_B& \\ & 0_{B\times B}\end{array}\right]F\left[\begin{array}{c}{l}_{0,n}^{⊺}\\ l_{1,n}^{⊺}\\ ⋮\\ l_{2B-1,n}^{⊺}\end{array}\right]\end{array}$$

对于每个块$n$，$\{{\hat{d}}_B,e_{B,n}\}$可以表示为：

$$\begin{gathered} {\hat{d}}_{B,n}=\text{col}\{\hat{d}(nB+B-1),...,\hat{d}(nB+1),\hat{d}(nB)\} \\ {e}_{B,n}=\text{col}\{e(nB+B-1),...,e(nB+1),e(nB)\} \end{gathered}$$

Block NLMS 自适应滤波器的实现代码如下所示：

import numpy as np
from numpy.fft import rfft as fft
from numpy.fft import irfft as ifft

def fdaf(x, d, M, mu=0.05, beta=0.9):
    """频域自适应滤波器: Block NLMS 自适应滤波器

    Args:
        x (_type_): 输入信号
        d (_type_): 期望信号
        M (_type_): FFT窗口尺寸
        mu (float, optional): 迭代步长. Defaults to 0.05.
        beta (float, optional): 正则化系数. Defaults to 0.9.
    """

    # 滤波器权重系数
    H = np.zeros(M+1, dtype=np.complex)
    # 正则化系数
    norm = np.full(M+1, 1e-8)

    # 窗口
    window = np.hanning(M)
    x_old = np.zeros(M)

    # 窗口块的个数
    num_block = min(len(x), len(d)) // M
    # 信号误差
    e = np.zeros(num_block * M)

    # 下面对每个块进行迭代
    for n in range(num_block):
        x_n = np.concatenate([x_old, x[n*M:(n+1)*M]])
        d_n = d[n*M:(n+1)*M]
        x_old = x[n*M:(n+1)*M]

        # 将每个窗口数据进行FFT变换，在频域与滤波器权重系数H相乘(对应于时域的卷积)
        X_n = fft(x_n)
        y_n = ifft(H*X_n)[M:]

        # 在时域得到每个窗口的信号误差
        e_n = d_n - y_n
        e[n*M:(n+1)*M] = e_n
        # 计算频域的误差信号
        e_fft = np.concatenate([np.zeros(M), e_n*window])
        E_n = fft(e_fft)

        # 计算频域的自适应滤波器权重系数
        norm = beta*norm + (1-beta)*np.abs(X_n)**2
        G = mu*E_n / (norm+1e-3)
        H = H + X_n.conj()*G

        # 计算时域的自适应滤波器权重
        h = ifft(H)
        h[M:] = 0
        H = fft(h)
    return e

参考文献

---

1. 自适应滤波器算法综述以及代码实现 - 凌逆战 - 博客园 ↩︎

2. 自适应滤波器（一）LMS自适应滤波器 - 知乎 ↩︎

3. (74条消息) python实现LMS、NLMS、RLS、KALMAN等自适应滤波器_ewan_xu的博客-CSDN博客_python实现lms算法 ↩︎