基于适应度值和迭代次数的动态惯性权值策略改进的飞蛾火焰优化算法
文章目录
- 一、理论基础
-
- 1、飞蛾火焰优化算法
- 2、改进的飞蛾火焰优化算法
-
- (1)动态惯性权值
- (2)AMFO算法
- 二、仿真实验与分析
- 三、参考文献
一、理论基础
1、飞蛾火焰优化算法
请参考这里。
2、改进的飞蛾火焰优化算法
(1)动态惯性权值
惯性权值参数对算法的全局和局部搜索有着重要影响。MFO算法中权值大小决定了上次迭代中火焰个体对本次迭代中飞蛾个体的影响程度。迭代初期,希望有较高的全局搜索能力以探索新的解空间,跳出局部极值;迭代后期,则重视局部开发以加快收敛并发现精确解。若MFO算法采用线性递减惯性权值,对于复杂高维函数,当迭代次数较大时,每次迭代的惯性权值的变化量较小,将影响权值调整策略功能的发挥;同时,单一的变化模式,在迭代后期,飞蛾在陷入局部最优后将很难飞出。基于上述分析,除了考虑算法所处的迭代阶段以外,还应该将飞蛾的适应度值考虑进去,即权值大小由迭代次数和飞蛾的适应度值共同决定。动态惯性权值 w w w描述如下: w i , j = exp ( f ( j ) / μ ) 2.4 + ( exp ( − f ( j ) / μ ) ) i t e r (1) w_{i,j}=\frac{\exp(f(j)/\mu)}{2.4+(\exp(-f(j)/\mu))^{iter}}\tag{1} wi,j=2.4+(exp(−f(j)/μ))iterexp(f(j)/μ)(1)
式中, μ \mu μ为第一次寻优过程的平均适应度值; f ( j ) f(j) f(j)为第 j j j个飞蛾的适应度值; i t e r iter iter表示当前迭代次数。针对极小值优化问题,设置飞蛾优化解对应的函数值为适应度值,随着迭代次数增加, f ( j ) f(j) f(j)呈现非线性减小趋势, 2.4 + ( e x p ( − f ( j ) / μ ) ) i t e r 2.4+(exp(-f(j)/\mu))^{iter} 2.4+(exp(−f(j)/μ))iter呈现非线性增加趋势,故权值 w w w随
着适应度值和迭代次数呈现非线性减小趋势。图1给出了动态惯性权值变化曲线。
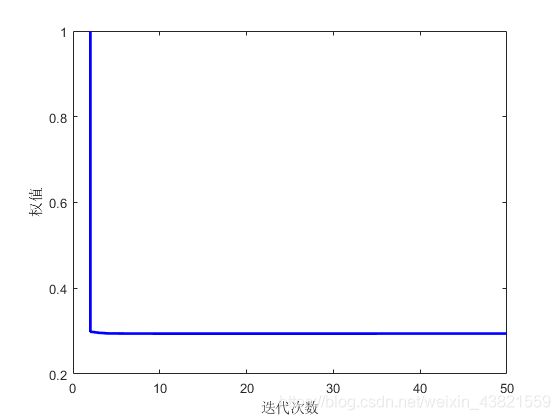
从图1中可以看出,开始迭代阶段, w w w值大于1,随着迭代次数和适应度值的变化,迅速减小, w w w值在迭代后期接近并稳定在0.294附近。改进后的位置更新公式如式(2)所示: S ( M i , F j ) = w i , j × D i × e b t × cos ( 2 π t ) + ( 1 − w i , j ) × F j (2) S(M_i,F_j)=w_{i,j}×D_i×e^{bt}×\cos(2\pi t)+(1-w_{i,j})×F_j\tag{2} S(Mi,Fj)=wi,j×Di×ebt×cos(2πt)+(1−wi,j)×Fj(2)动态惯性权值随着迭代次数和适应度值非线性动态变化,人工飞蛾逐渐向适应度值较优的火焰运动,利于MFO算法的性能提升。
(2)AMFO算法
基于上述描述,AMFO算法流程描述如下:
(1)初始化算法参数:飞蛾数量 n n n、维数 d d d、最大迭代次数 T T T等;
(2)种群初始化;
(3)计算种群中人工飞蛾和人工火焰的适应度值,并按适应度值排序;
(4)更新火焰最优解和火焰数量;
(5)按式(1)更新动态惯性权值;
(6)按式(2)更新飞蛾位置;
(7)若满足终止条件,算法结束,获得最优解,否则返回步骤(3)。
二、仿真实验与分析
对表1中8个测试函数进行测试。
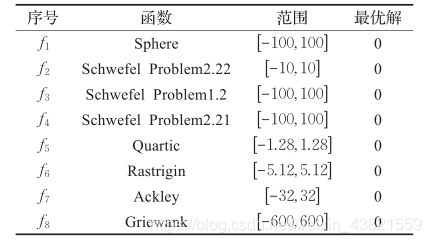 为了说明AMFO算法的有效性,将AMFO与MFO算法、PSO算法和DE算法进行比较。PSO算法设置 c 1 = c 2 = 1.5 , w ′ = 0.9 , w ′ ′ = 0.4 c_1=c_2=1.5,w'=0.9,w''=0.4 c1=c2=1.5,w′=0.9,w′′=0.4;DE算法设置 F = 0.6 , C r = 0.85 F=0.6,Cr=0.85 F=0.6,Cr=0.85;MFO和AMFO算法设置 b = 1 b=1 b=1。四种优化算法种群规模为40,迭代次数为1000。对于表1的8个测试函数,维度设置为10。四种算法均独立运行30次, 记录并保存最佳解的最大值、最小值、平均值和标准差。
为了说明AMFO算法的有效性,将AMFO与MFO算法、PSO算法和DE算法进行比较。PSO算法设置 c 1 = c 2 = 1.5 , w ′ = 0.9 , w ′ ′ = 0.4 c_1=c_2=1.5,w'=0.9,w''=0.4 c1=c2=1.5,w′=0.9,w′′=0.4;DE算法设置 F = 0.6 , C r = 0.85 F=0.6,Cr=0.85 F=0.6,Cr=0.85;MFO和AMFO算法设置 b = 1 b=1 b=1。四种优化算法种群规模为40,迭代次数为1000。对于表1的8个测试函数,维度设置为10。四种算法均独立运行30次, 记录并保存最佳解的最大值、最小值、平均值和标准差。
结果显示如下:
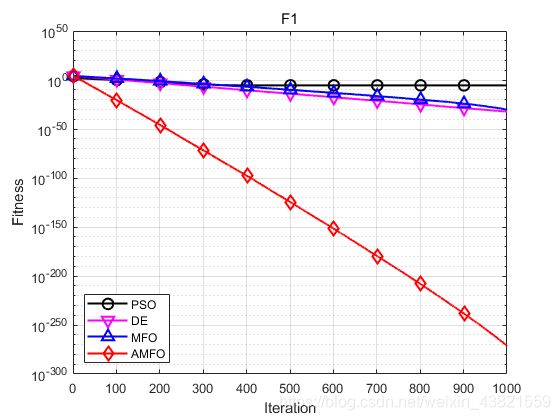




函数:F1
PSO:最大值: 8.4983e-05,最小值:1.1546e-10,平均值:3.2292e-06,标准差:1.5481e-05
DE:最大值: 8.7146e-32,最小值:2.3194e-35,平均值:6.6497e-33,标准差:1.6238e-32
MFO:最大值: 2.696e-30,最小值:4.4738e-34,平均值:4.9164e-31,标准差:7.6557e-31
AMFO:最大值: 5.589e-271,最小值:2.6632e-277,平均值:3.7055e-272,标准差:0
函数:F2
PSO:最大值: 0.26615,最小值:0.0036761,平均值:0.078469,标准差:0.078358
DE:最大值: 3.7714e-17,最小值:1.6988e-18,平均值:1.2862e-17,标准差:9.3978e-18
MFO:最大值: 1.5563e-18,最小值:4.8763e-21,平均值:3.4001e-19,标准差:3.8187e-19
AMFO:最大值: 1.6438e-146,最小值:5.0147e-152,平均值:8.5459e-148,标准差:3.0028e-147
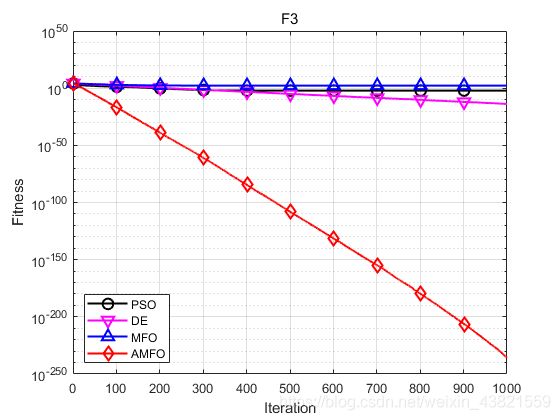
函数:F3
PSO:最大值: 0.054229,最小值:6.8676e-10,平均值:0.0076137,标准差:0.013037
DE:最大值: 8.9015e-14,最小值:1.3047e-16,平均值:1.5338e-14,标准差:2.0193e-14
MFO:最大值: 5000,最小值:8.5859e-13,平均值:166.6667,标准差:912.8709
AMFO:最大值: 2.2061e-235,最小值:9.6136e-242,平均值:1.4643e-236,标准差:0
函数:F4
PSO:最大值: 2.5346,最小值:0.011349,平均值:0.47454,标准差:0.47791
DE:最大值: 1.8221e-10,最小值:5.3534e-12,平均值:5.0468e-11,标准差:3.5962e-11
MFO:最大值: 8.3859,最小值:1.035e-08,平均值:0.33042,标准差:1.5302
AMFO:最大值: 7.4133e-137,最小值:6.5523e-142,平均值:7.1406e-138,标准差:1.5635e-137
函数:F5
PSO:最大值: 0.0067951,最小值:0.00053889,平均值:0.0026584,标准差:0.0017408
DE:最大值: 0.028654,最小值:0.0015815,平均值:0.011146,标准差:0.0059163
MFO:最大值: 0.0096477,最小值:0.0010157,平均值:0.0040222,标准差:0.0023624
AMFO:最大值: 0.00010438,最小值:2.5904e-06,平均值:2.5711e-05,标准差:2.6951e-05
函数:F6
PSO:最大值: 15.9193,最小值:1.9899,平均值:10.019,标准差:3.7335
DE:最大值: 31.9501,最小值:1.8089,平均值:19.3475,标准差:6.6745
MFO:最大值: 48.8239,最小值:5.9698,平均值:20.6027,标准差:11.4578
AMFO:最大值: 0,最小值:0,平均值:0,标准差:0
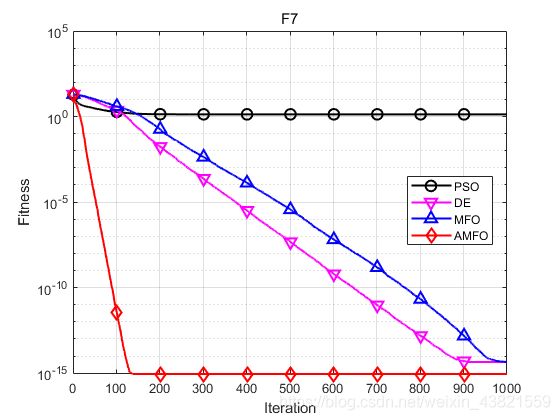
函数:F7
PSO:最大值: 3.0266,最小值:2.5307e-06,平均值:1.344,标准差:0.94939
DE:最大值: 4.4409e-15,最小值:4.4409e-15,平均值:4.4409e-15,标准差:0
MFO:最大值: 7.9936e-15,最小值:4.4409e-15,平均值:4.5593e-15,标准差:6.4863e-16
AMFO:最大值: 8.8818e-16,最小值:8.8818e-16,平均值:8.8818e-16,标准差:0
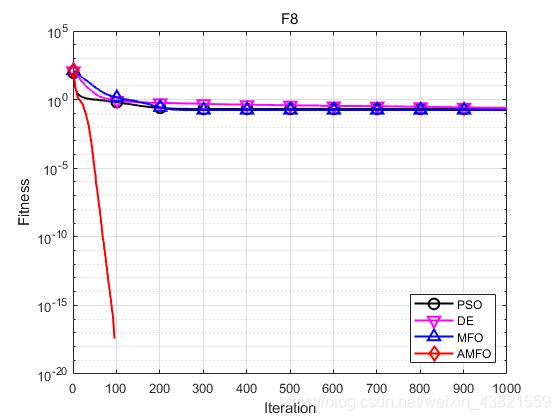
函数:F8
PSO:最大值: 0.48236,最小值:0.027052,平均值:0.20612,标准差:0.11358
DE:最大值: 0.43513,最小值:0.012316,平均值:0.24793,标准差:0.12992
MFO:最大值: 0.63978,最小值:0.032006,平均值:0.17322,标准差:0.12678
AMFO:最大值: 0,最小值:0,平均值:0,标准差:0
综上所述,AMFO算法能够有效地找到全局最优值或接近理论最优值,提出的AMFO算法的改进策略是成功的,针对函数优化问题,AMFO是一个非常高效的优化算法。
三、参考文献
[1] 田鸿, 陈国彬, 刘超. 新型飞蛾火焰优化算法的研究[J]. 计算机工程与应用, 2019, 55(16): 138-143.