【自然语言处理】深度学习基础

01. 引入

神经网络处理文本：字符串分类 - 判断字符串中是否出现了指定字符

例：指定字符a样本：

abcd 正样本

bcde 负样本

当前输入：字符串abcd

预期输出：概率值 正样本=1，负样本=0，以0.5为分界

X = “abcd” Y = 1

X =“bcde” Y = 0

建模目标：找到一个映射f(x)，使得f(“abcd”) = 1, f(“bcde”) = 0

①字符数值化直观方式，a -> 1, b -> 2, c -> 3 …. z -> 26 不太合理，因为数值化之后每个字母之间就有一定的等式关系

每个字符转化成同维度向量a - > [0.32618175 0.20962898 0.43550067 0.07120884 0.58215387]、b - > [0.21841921 0.97431001 0.43676452 0.77925024 0.7307891 ]、 …、z -> [0.72847746 0.72803551 0.43888069 0.09266955 0.65148562]

字符数值化“abcd” - > 4 * 5 的矩阵 [[0.32618175 0.20962898 0.43550067 0.07120884 0.58215387] [0.21841921 0.97431001 0.43676452 0.77925024 0.7307891 ] [0.95035602 0.45280039 0.06675379 0.72238734 0.02466642] [0.86751814 0.97157839 0.0127658 0.98910503 0.92606296]]

矩阵形状 = 文本长度 * 向量长度

②矩阵转化为向量求平均(池化过程)

[[0.32618175 0.20962898 0.43550067 0.07120884 0.58215387] [0.21841921 0.97431001 0.43676452 0.77925024 0.7307891 ] [0.95035602 0.45280039 0.06675379 0.72238734 0.02466642] [0.86751814 0.97157839 0.0127658 0.98910503 0.92606296]]- >[0.59061878 0.65207944 0.2379462 0.64048786 0.56591809]（相加除以四）

由4 * 5 矩阵 -> 1* 5 向量 形状 = 1*向量长度

③向量到数值采取最简单的线性公式 y = w * x + b

w 维度为1*向量维度，b为实数例：

w = [1, 1], b = -1, x = [1,2]、

[1,1] * [1 2] - 1 = 1*1 + 1*2 - 1 = 2

④数值归一化

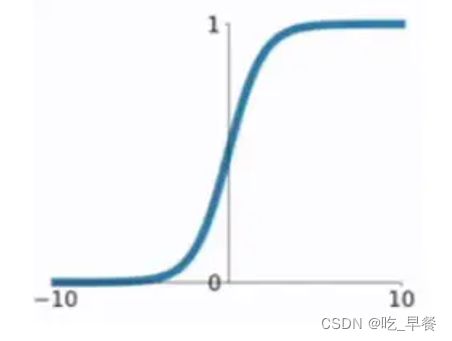
sigma函数
$$\sigma (x)=\frac{1}{1+e^{-x}}$$
x = 3 σ(x) = 0.9526

整体映射

“abcd” ----每个字符转化成向量（Embedding层）----> 4 * 5矩阵

4 * 5矩阵 ----向量求平均（池化层）----> 1 * 5向量

1 * 5向量 ----w*x + b线性公式 —> 实数

实数 ----sigmoid归一化函数—> 0-1之间实数

加粗部分需要通过训练优化

02. 神经网络

2.1 Embedding层

Embedding矩阵是可训练的参数，一般会在模型构建时随机初始化，也可以使用预训练的词向量来做初始化，此时也可以选择不训练Embedding层中的参数

输入的整数序列可以有重复，但取值不能超过Embedding矩阵的列数

核心价值：将离散值转化为向量

#coding:utf8
import torch
import torch.nn as nn

'''
embedding层的处理
'''

num_embeddings = 6  #通常对于nlp任务，此参数为字符集字符总数
embedding_dim = 3   #每个字符向量化后的向量维度
embedding_layer = nn.Embedding(num_embeddings, embedding_dim)
print(embedding_layer.weight, "随机初始化权重")

#构造输入
x = torch.LongTensor([[1,2,3],[2,2,0]])
embedding_out = embedding_layer(x)# 传入构造的embedding_layer层
print(embedding_out)

运行结果：

Parameter containing:
tensor([[-1.6804, -1.7307, -1.2290],
        [-0.3990,  0.4878,  2.5067],
        [-1.5682, -2.1808,  0.2217],
        [-1.1663, -1.5519, -0.6108],
        [-0.0392, -0.1552,  2.2150],
        [ 0.5951,  0.6064, -0.2041]], requires_grad=True) 随机初始化权重
tensor([[[-0.3990,  0.4878,  2.5067],
         [-1.5682, -2.1808,  0.2217],
         [-1.1663, -1.5519, -0.6108]],

        [[-1.5682, -2.1808,  0.2217],
         [-1.5682, -2.1808,  0.2217],
         [-1.6804, -1.7307, -1.2290]]], grad_fn=)

2.2 网络结构

2.2.1 网络结构-DNN

全连接层又称线性层，计算公式：y = w * x + b

W和b是参与训练的参数，W的维度决定了隐含层输出的维度，一般称为隐单元个数（hidden size）

举例：输入：x （维度1 x 3）隐含层1：w（维度3 x 5）隐含层2: w（维度5 x 2）DNN-numpy手动实现模拟一个线性层

#coding:utf8

import torch
import torch.nn as nn
import numpy as np

"""
numpy手动实现模拟一个线性层
"""

#搭建一个2层的神经网络模型
#每层都是线性层
# 定义类，然后继承nn.Module类
class TorchModel(nn.Module):
    # 定义组件
    def __init__(self, input_size, hidden_size1, hidden_size2):
        super(TorchModel, self).__init__()
        # 第一层input_size维映射到hidden_size1维
        self.layer1 = nn.Linear(input_size, hidden_size1)
        # 第二层hidden_size1维映射到hidden_size2维···以此类推
        self.layer2 = nn.Linear(hidden_size1, hidden_size2)

	#堆叠积木
    def forward(self, x):
        # 第一层输入的值传入隐藏层
        hidden = self.layer1(x)   #shape: (batch_size, input_size) -> (batch_size, hidden_size1)
        # 输入隐藏层得到预测值
        y_pred = self.layer2(hidden) #shape: (batch_size, hidden_size1) -> (batch_size, hidden_size2)
        return y_pred

#随便准备一个网络输入
x = np.array([1, 0, 2])
print(x)
#建立torch模型
torch_model = TorchModel(len(x), 5, 2)
print(torch_model.state_dict())# state_dict()存放训练过程中需要学习的权重和偏执系数
print("-----------")
#打印模型权重，权重为随机初始化
torch_model_w1 = torch_model.state_dict()["layer1.weight"].numpy()
torch_model_b1 = torch_model.state_dict()["layer1.bias"].numpy()
torch_model_w2 = torch_model.state_dict()["layer2.weight"].numpy()
torch_model_b2 = torch_model.state_dict()["layer2.bias"].numpy()
print(torch_model_w1, "torch w1 权重")
print(torch_model_b1, "torch b1 权重")
print("-----------")
print(torch_model_w2, "torch w2 权重")
print(torch_model_b2, "torch b2 权重")
print("-----------")
#使用torch模型做预测
torch_x = torch.FloatTensor(np.array([x]))
y_pred = torch_model.forward(torch_x)
print("torch模型预测结果：", y_pred)
#把torch模型权重拿过来自己实现计算过程

自定义模型，就是不使用接口将以上模型写出来

class DiyModel:
    def __init__(self, w1, b1, w2, b2):
        self.w1 = w1
        self.b1 = b1
        self.w2 = w2
        self.b2 = b2

    def forward(self, x):
        hidden = np.dot(x, self.w1.T) + self.b1 # dot函数计算的是两个数组的点积
        y_pred = np.dot(hidden, self.w2.T) + self.b2
        return y_pred

2.2.2 网络结构-RNN

循环神经网络（recurrent neural network）

主要思想：将整个序列划分成多个时间步，将每一个时间步的信息依次输入模型，同时将模型输出的结果传给下一个时间步。

公式：（有时b可省略）
$$h^{(t)}=tanh(b+W{h}^{(t-1)}+U{x}^{(t)})$$
模型：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

注意：一般都是先RNN再Polling。因为如果先pooling的话RNN时就会缺少部分数据，这不是RNN的初衷

使用封装模型

#coding:utf8

import torch
import torch.nn as nn
import numpy as np


"""
使用pytorch实现RNN
"""
# 搭建模型
class TorchRNN(nn.Module):
    def __init__(self, input_size, hidden_size):
        super(TorchRNN, self).__init__()
        self.layer = nn.RNN(input_size, hidden_size, bias=False, batch_first=True)

    def forward(self, x):
        return self.layer(x)


x = np.array([[1, 2, 3],
              [3, 4, 5],
              [5, 6, 7]])  #网络输入

#torch实验
hidden_size = 4
torch_model = TorchRNN(3, hidden_size)
print(torch_model.state_dict())
w_ih = torch_model.state_dict()["layer.weight_ih_l0"]
w_hh = torch_model.state_dict()["layer.weight_hh_l0"]

torch_x = torch.FloatTensor(np.array([x]))
output, h = torch_model.forward(torch_x)
print(h)
print(output.detach().numpy(), "torch模型预测结果")
print(h.detach().numpy(), "torch模型预测隐含层结果")

手动建模型

#自定义RNN模型，就是用来做个对比，以后的项目中不需要这一步
#w_ih就是公式中的u，W_hh就是公式中的w
class DiyModel:
    def __init__(self, w_ih, w_hh, hidden_size):
        self.w_ih = w_ih
        self.w_hh = w_hh
        self.hidden_size = hidden_size

    def forward(self, x):
        ht = np.zeros((self.hidden_size))
        output = []
        #公式的复现
        for xt in x:
            ux = np.dot(self.w_ih, xt)
            wh = np.dot(self.w_hh, ht)
            ht_next = np.tanh(ux + wh)
            output.append(ht_next)
            ht = ht_next
        return np.array(output), ht

注意：

①RNN不建议堆叠得很深，大概三层就够了，因为效率不是很高

②RNN可以认为是把每个向量的第一维取出，依次取出每一维

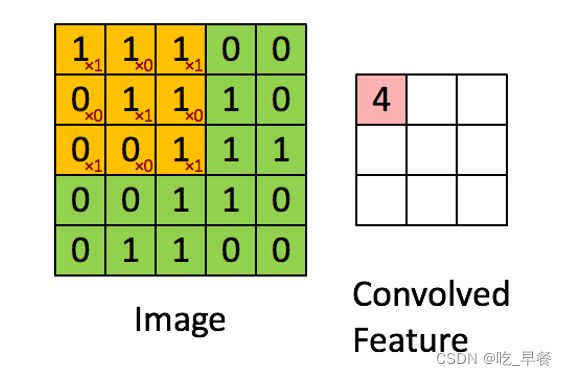
2.2.3 网络结构-CNN

以卷积操作为基础的网络结构，每个卷积核可以看成一个特征提取器

CNN模型

#coding:utf8

import torch
import torch.nn as nn
import numpy as np


"""
手动实现简单的神经网络
使用pytorch实现CNN
手动实现CNN
对比
"""
# in_channel：加入是一张灰度图，就是一个单通道的图，值为1
class TorchCNN(nn.Module):
    def __init__(self, in_channel, out_channel, kernel):
        super(TorchCNN, self).__init__()
        self.layer = nn.Conv2d(in_channel, out_channel, kernel, bias=False)

    def forward(self, x):
        return self.layer(x)



x = np.array([[0.1, 0.2, 0.3, 0.4],
              [-3, -4, -5, -6],
              [5.1, 6.2, 7.3, 8.4],
              [-0.7, -0.8, -0.9, -1]])  #网络输入

#torch实验
in_channel = 1
out_channel = 3 #三个卷积核
kernel_size = 2 #2*2的卷积核
torch_model = TorchCNN(in_channel, out_channel, kernel_size)
print(torch_model.state_dict())#打印权重
torch_w = torch_model.state_dict()["layer.weight"]
print(torch_w.numpy().shape)
torch_x = torch.FloatTensor([[x]])
output = torch_model.forward(torch_x)
output = output.detach().numpy()
print(output, output.shape, "torch模型预测结果\n")
print("---------------")
diy_model = DiyModel(x.shape[0], x.shape[1], torch_w, kernel_size)
output = diy_model.forward(x)
print(output, "diy模型预测结果")

自定义CNN模型

class DiyModel:
    def __init__(self, input_height, input_width, weights, kernel_size):
        self.height = input_height
        self.width = input_width
        self.weights = weights#对应的权重
        self.kernel_size = kernel_size

    def forward(self, x):
        output = []
        for kernel_weight in self.weights:
            kernel_weight = kernel_weight.squeeze().numpy() #shape : 2x2
            kernel_output = np.zeros((self.height - kernel_size + 1, self.width - kernel_size + 1))
            for i in range(self.height - kernel_size + 1):
                for j in range(self.width - kernel_size + 1):
                    window = x[i:i+kernel_size, j:j+kernel_size]
                    kernel_output[i, j] = np.sum(kernel_weight * window) # np.dot(a, b) != a * b
            output.append(kernel_output)
        return np.array(output)

2.2.4 总结

网络结构的理解：不同的网络结构区别就是不同的函数，就会出现不同的参数

以DNN为例解释代码模型结构

# 定义类，然后继承nn.Module类
class TorchModel(nn.Module):
    # 定义组件
    def __init__(self, input_size, hidden_size1, hidden_size2):
        super(TorchModel, self).__init__()
        # 第一层input_size维映射到hidden_size1维
        self.layer1 = nn.Linear(input_size, hidden_size1)
        # 第二层hidden_size1维映射到hidden_size2维···以此类推
        self.layer2 = nn.Linear(hidden_size1, hidden_size2)
	# 堆叠积木
    def forward(self, x):
        # 第一层输入的值传入隐藏层
        hidden = self.layer1(x)   #shape: (batch_size, input_size) -> (batch_size, hidden_size1)
        # 输入隐藏层得到预测值
        y_pred = self.layer2(hidden) #shape: (batch_size, hidden_size1) -> (batch_size, hidden_size2)
        return y_pred

2.3 池化层

降维：降低了后续网络层的输入维度，缩减模型大小，提高计算速度

防止过拟合：提高了Feature Map 的鲁棒性，防止过拟合

pooling层

#coding:utf8
import torch
import torch.nn as nn

'''
pooling层的处理
'''

#pooling操作默认对于输入张量的最后一维进行
#入参5，代表把五维池化为一维
layer = nn.AvgPool1d(5)# 取平均；MaxPool1d()取最大值
#随机生成一个维度为3x4x5的张量
#可以想象成3条,文本长度为4,向量长度为5的样本
x = torch.rand([3, 4, 5])
print(x)
print(x.shape)
#经过pooling层
y = layer(x)
print(y)
print(y.shape)
#squeeze方法去掉值为1的维度
y = y.squeeze()
print(y)
print(y.shape)

运行结果：

tensor([[[0.8307, 0.1603, 0.7290, 0.4198, 0.1470],
         [0.6383, 0.1021, 0.2992, 0.7656, 0.5260],
         [0.6156, 0.3681, 0.9710, 0.4929, 0.9303],
         [0.2452, 0.4174, 0.6035, 0.8790, 0.6109]],

        [[0.6634, 0.4503, 0.0455, 0.1194, 0.2872],
         [0.7791, 0.5386, 0.7341, 0.5429, 0.3587],
         [0.2208, 0.2353, 0.7941, 0.1140, 0.5503],
         [0.8110, 0.3359, 0.3486, 0.7482, 0.3088]],

        [[0.9698, 0.8568, 0.0981, 0.3720, 0.7700],
         [0.3536, 0.7100, 0.6332, 0.5188, 0.3759],
         [0.2450, 0.7529, 0.5502, 0.4768, 0.3968],
         [0.3272, 0.5425, 0.6530, 0.9158, 0.0884]]])
torch.Size([3, 4, 5])
tensor([[[0.4573],
         [0.4662],
         [0.6756],
         [0.5512]],

        [[0.3132],
         [0.5907],
         [0.3829],
         [0.5105]],

        [[0.6134],
         [0.5183],
         [0.4843],
         [0.5054]]])
torch.Size([3, 4, 1])
tensor([[0.4573, 0.4662, 0.6756, 0.5512],
        [0.3132, 0.5907, 0.3829, 0.5105],
        [0.6134, 0.5183, 0.4843, 0.5054]])
torch.Size([3, 4])

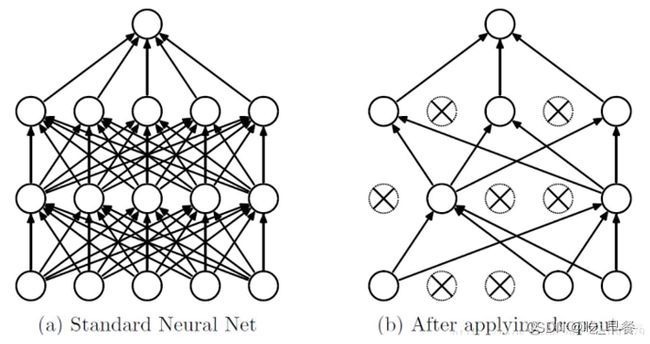
2.4 Dropout层

作用：减少过拟合

按照指定概率，随机丢弃一些神经元（将其化为零）

其余元素乘以 1 / (1 – p)进行放大（如果不放大的话，在量级上就会有差别）

#coding:utf8

import torch
import torch.nn as nn
import numpy as np


"""
基于pytorch的网络编写
测试dropout层
"""

import torch

x = torch.Tensor([1,2,3,4,5,6,7,8,9])
dp_layer = torch.nn.Dropout(0.5)# p=0.5 ，代入公式算出翻两倍
dp_x = dp_layer(x)
print(dp_x)

如何理解其作用：

1）强迫一个神经单元，和随机挑选出来的其他神经单元共同工作，消除减弱了神经元节点间的联合适应性，增强了泛化能力

2）可以看做是一种模型平均，由于每次随机忽略的隐层节点都不同，这样就使每次训练的网络都是不一样的，每次训练都可以单做一个“新”的模型

计算方式并不是越复杂就越好

2.5 激活函数

为模型添加非线性因素，使模型具有拟合非线性函数的能力

无激活函数时 y = w1(w2(w3 * x + b3) +b2) + b1 仍然是线性函数

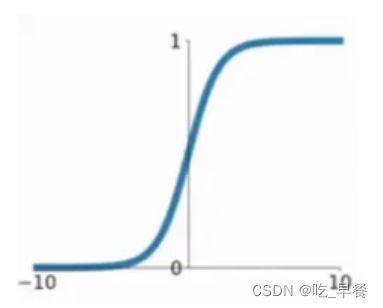
2.5.1 Sigmoid

将任意输入映射到0-1之间。函数值连续，可导

缺点：

1.计算耗时，包含指数运算

2.非0均值，会导致收敛慢

3.易造成梯度消失
$$\sigma (x)=\frac{1}{1+e^{-x}}$$

2.5.2 tanh

以0为均值，解决了sigmoid的一定缺点，但是依然存在梯度消失问题

计算同样非常耗时
$$tanh(x)=\frac{sinh(x)}{cosh(x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

2.5.3 Relu

在正区间不易发生梯度消失

计算速度非常快

一定程度上降低过拟合的风险
$$Relu=max(0,x)$$

2.6 损失函数

2.6.1 均方差

MSE mean square error 对均方差在做开根号，可以得到根方差

一般用于0~1之间的数字
$$l(x,y)=L=\{l_1,\cdot \cdot \cdot ,l_N{\}}^T,l_n=(x_n-y_n{)}^2$$

$$l(x,y)=\{\begin{array}{c}mean(L),ifreduction{=}^{\prime }mea{n}^{\prime }\\ sum(L),ifreduction{=}^{\prime }su{m}^{\prime }\end{array}$$

    #手动实现mse，均方差loss
    def diy_mse_loss(self, y_pred, y_true):
        return np.sum(np.square(y_pred - y_true)) / len(y_pred)

2.6.2 交叉熵

Cross Entropy常用于分类任务

分类任务中，网络输出经常是所有类别上的概率分布

公式：
$$H(p,q)=-\sum _{x}p(x)logq(x)$$
假设一个三分类任务，某样本的正确标签是第一类，则p = [1, 0, 0], 模型预测值假设为[0.5, 0.4, 0.1], 则交叉熵计算如下：
$$H(p=[1,0,0],q=[0.5,0.4,0.1])=-(1\ast log0.5+0\ast log0.4+0\ast log0.1)\approx 0.3$$

import torch
import torch.nn as nn
import numpy as np

#使用torch计算交叉熵
ce_loss = nn.CrossEntropyLoss()
#假设有3个样本，每个都在做3分类
pred = torch.FloatTensor([[0.0, 0.1, 0.3],
                          [0.9, 0.2, 0.9],
                          [0.5, 0.4, 0.2]])
#正确的类别分别为1,2,0
target = torch.LongTensor([1, 2, 0])
loss = ce_loss(pred, target)
print(loss, "torch输出交叉熵")


#实现softmax函数
def softmax(matrix):
    return np.exp(matrix) / np.sum(np.exp(matrix), axis=1, keepdims=True)

#验证softmax函数
# print(torch.softmax(pred, dim=1))
# print(softmax(pred.numpy()))


#将输入转化为onehot矩阵
def to_one_hot(target, shape):
    one_hot_target = np.zeros(shape)
    for i, t in enumerate(target):
        one_hot_target[i][t] = 1
    return one_hot_target

#手动实现交叉熵
def cross_entropy(pred, target):
    batch_size, class_num = pred.shape
    pred = softmax(pred)
    target = to_one_hot(target, pred.shape)
    entropy = - np.sum(target * np.log(pred), axis=1)
    return sum(entropy) / batch_size

print(cross_entropy(pred.numpy(), target.numpy()), "手动实现交叉熵")

2.6.3 其他

指数损失:
$$L(Y,f(X))=exp(-Yf(X))$$
对数损失
$$L(Y,P(Y|X))=-logP(Y|X)$$
0/1损失
$$L(Y,f(X))=\{\begin{array}{c}1,Y\ne f(X)\\ 0,Y=f(X)\end{array}$$

Hinge损失（二分类）
$$J_{hinge}=\sum _{i=1}^{N}max(0,1-sgn(y_i)\widehat{y_i})$$

2.7 优化器

根据梯度，控制调整权重的幅度

2.7.1 SGD

SGD (Stochastic gradient descent)：权重=权重-学习率×梯度

$${\theta }_{t+1}={\theta }_t-\alpha ▽L({\theta }_t)$$

#梯度更新
def diy_sgd(grad, weight, learning_rate):
    return weight - learning_rate * grad

2.7.2 Adam

1. 实现简单，计算高效，对内存需求少
2. 超参数具有很好的解释性，且通常无需调整或仅需很少的微调
3. 更新的步长能够被限制在大致的范围内（初始学习率）
4. 能够表现出自动调整学习率
5. 很适合应用于大规模的数据及参数的场景
6. 适用于不稳定目标函数
7. 适用于梯度稀疏或梯度存在很大噪声的问题

#adam梯度更新
def diy_adam(grad, weight):
    #参数应当放在外面，此处为保持后方代码整洁简单实现一步
    alpha = 1e-3  #学习率
    beta1 = 0.9   #超参数
    beta2 = 0.999 #超参数
    eps = 1e-8    #超参数，是一个特别小的值，后续为了防止分母为零
    t = 0         #初始化
    mt = 0        #初始化
    vt = 0        #初始化
    #开始计算
    t = t + 1
    gt = grad   # 梯度
    mt = beta1 * mt + (1 - beta1) * gt  # 加上前面的梯度然后再加当前梯度
    vt = beta2 * vt + (1 - beta2) * gt ** 2
    mth = mt / (1 - beta1 ** t) # 混合后的梯度
    vth = vt / (1 - beta2 ** t)# 使训练先快后慢，慢点走；
    weight = weight - (alpha / (np.sqrt(vth) + eps)) * mth# 括号里的代表学习率
    return weight

2.7.3 SGD与Adam对比

权重=权重-学习率×梯度

SGD：weight - learning_rate * grad

Adam： weight - (alpha / (np.sqrt(vth) + eps)) * mth

Adam优点：

①Adam的学习率为(alpha / (np.sqrt(vth) + eps))，是一个自动调整的过程

②Adam的梯度 mth = mt / (1 - beta1 ** t) 是与前面训练出来的梯度混合之后的梯度

2.8 完整的反向传播过程

1.根据输入x和模型当前权重，计算预测值y’

2.根据y’和y使用loss函数计算loss

3.根据loss计算模型权重的梯度

4.使用梯度和学习率，根据优化器调整模型权重

    #手动实现梯度计算
    def calculate_grad(self, y_pred, y_true, x):
        #前向过程
        # wx = np.dot(self.weight, x)
        # sigmoid_wx = self.diy_sigmoid(wx)
        # loss = self.diy_mse_loss(sigmoid_wx, y_true)
        #反向过程
        # 均方差函数 (y_pred - y_true) ^ 2 / n 的导数 = 2 * (y_pred - y_true) / n
        grad_loss_sigmoid_wx = 2/len(x) * (y_pred - y_true)
        # sigmoid函数 y = 1/(1+e^(-x)) 的导数 = y * (1 - y)
        grad_sigmoid_wx_wx = y_pred * (1 - y_pred)
        # wx对w求导 = x
        grad_wx_w = x
        #导数链式相乘
        grad = grad_loss_sigmoid_wx * grad_sigmoid_wx_wx
        grad = np.dot(grad.reshape(len(x),1), grad_wx_w.reshape(1,len(x)))
        return grad