卷积（Convolution）（二）

转置卷积（Transpose Convolution）

转置卷积提出背景

通常情况下，对图像进行卷积运算时，经过多层的卷积运算后，输出图像的尺寸会变得很小，即图像被约减。而对于某些特定的任务（比如：图像分割、GAN），我们需要将图像恢复到原来的尺寸再进行进一步的计算。这个恢复图像尺寸，实现图像由小分辨率到大分辨率映射的操作，叫做上采样（Upsample），如下图所示。

上采样有多种方式，常见的包括：最近邻插值（Nearest neighbor interpolation）、双线性插值（Bi-Linear interpolation）等，但是这些上采样方法都是基于人们的先验经验来设计的，对于很多场景效果并不理想。因此，我们希望让神经网络自己学习如何更好地进行插值，这也就是接下来要介绍的转置卷积（Transpose Convolution）的方法。

转置卷积及其应用

转置卷积（Transpose Convolution），在某些文献中也被称为反卷积（Deconvolution）。转置卷积中，不会使用预先设定的插值方法，它具有可学习的参数，通过让网络自行学习，来获取最优的上采样方式。转置卷积在某些特定的领域有着非常广泛的应用，比如：

• 在DCGAN，生成器将会用随机值转变为一个全尺寸(full-size)的图片，这个时候就需要用到转置卷积。

• 在语义分割中，会使用卷积层在编码器中进行特征提取，然后在解码层中进行恢复为原先的尺寸，这样才可以对原来图像的每个像素都进行分类。这个过程同样需要用到转置卷积。经典方法如：FCN和Unet。

• CNN的可视化：通过转置卷积将CNN中得到的特征图还原到像素空间，以观察特定的特征图对哪些模式的图像敏感。

转置卷积与标准卷积的区别

标准卷积的运算操作其实就是对卷积核中的元素与输入矩阵上对应位置的元素进行逐像素的乘积并求和。然后使用卷积核在输入矩阵上以步长为单位进行滑动，直到遍历完输入矩阵的所有位置。

这里举一个简单的例子演示一下具体的操作过程。假设输入是一个4×4的矩阵，使用3×3的标准卷积进行计算，同时不使用填充，步长设置为1。最终输出的结果应该是一个2×2的矩阵，如下图所示。

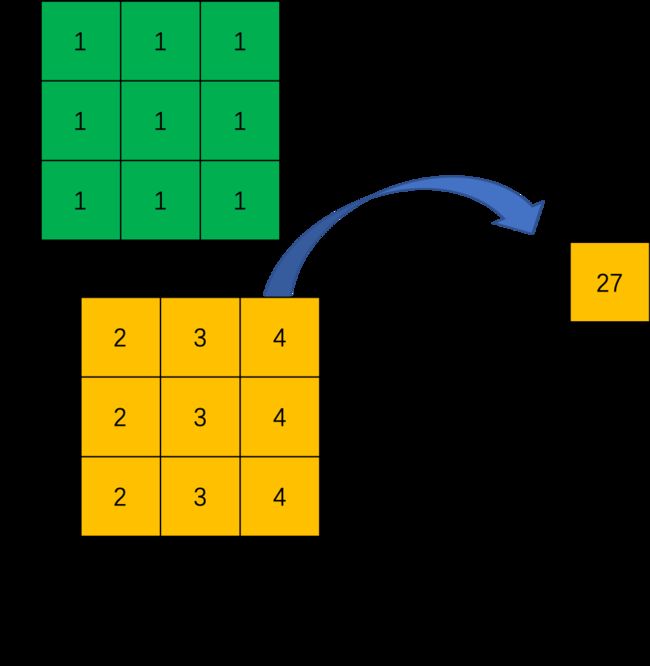
在上边的例子中，输入矩阵右上角3×3的值会影响输出矩阵中右上角的值，这其实也就对应了标准卷积中感受野的概念。所以，我们可以说3×3的标准卷积核建立了输入矩阵中9个值与输出矩阵中1个值的对应关系。

综上所述，我们也就可以认为标准卷积操作实际上就是建立了一个多对一的关系。

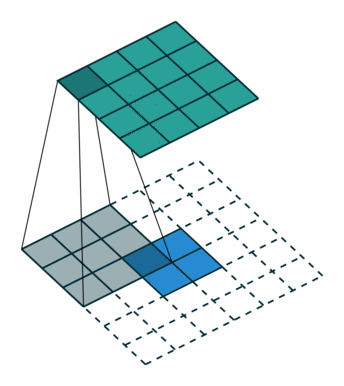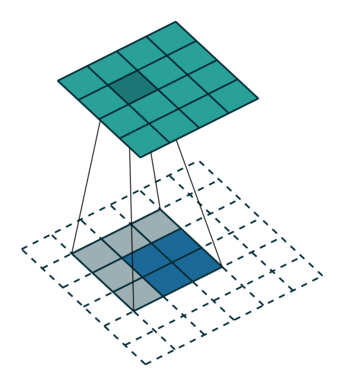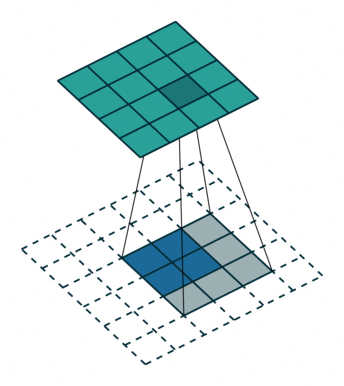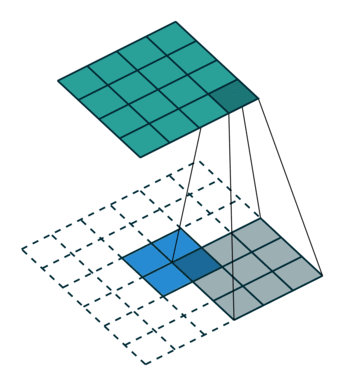
对于转置卷积而言，我们实际上是想建立一个逆向操作，也就是建立一个一对多的关系。对于上边的例子，我们想要建立的其实是输出卷积中的1个值与输入卷积中的9个值的关系，如下图所示。

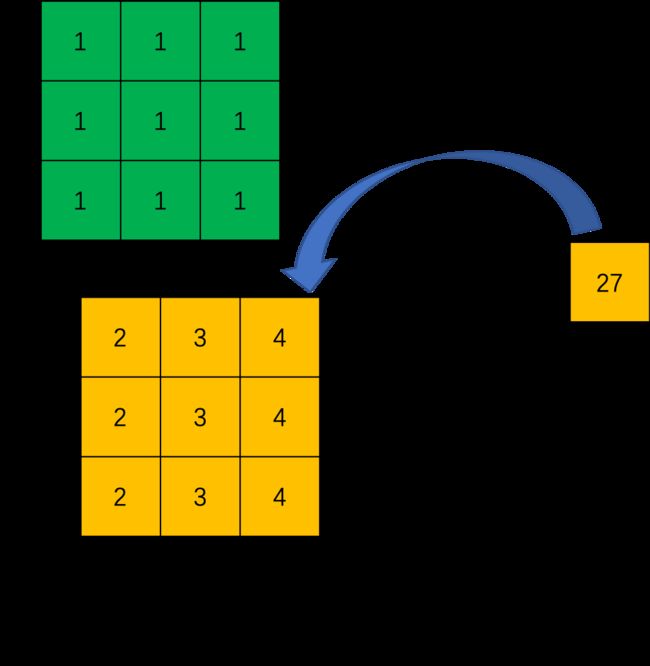
当然，从信息论的角度，卷积操作是不可逆的，所以转置卷积并不是使用输出矩阵和卷积核计算原始的输入矩阵，而是计算得到保持了相对位置关系的矩阵。

转置卷积数学推导

定义一个尺寸为$4\times 4$ 的输入矩阵 $input$：$$input=\left[\begin{array}{cccc}{x}_1& x_2& x_3& x_4\\ x_6& x_7& x_8& x_9\\ x_{10}& x_{11}& x_{12}& x_{13}\\ x_{14}& x_{15}& x_{16}& x_{17}\end{array}\right]$$ 一个尺寸为$3\times 3$ 的标准卷积核$$kernel=\left[\begin{array}{ccc}{w}_{0,0}& w_{0,1}& w_{0,2}\\ w_{1,0}& w_{1,1}& w_{1,2}\\ w_{2,0}& w_{2,1}& w_{2,2}\end{array}\right]$$令步长 stride=1，填充padding=0，按照输出特征图的计算方式$o=\frac{i+2p-k}{s}+1$，我们可以得到尺寸为 2×2 的输出矩阵 output ：$$output=\left[\begin{array}{cc}{y}_0& y_1\\ y_2& y_3\end{array}\right]$$ 这里，我们换一个表达方式，我们将输入矩阵 $input$ 和输出矩阵 $output$ 展开成列向量$X$ 和列向量$Y$ ，那么向量$X$ 和向量$Y$ 的尺寸就分别是$16\times 1$ 和$4\times 1$，可以分别用如下公式表示：$$X=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_6\\ x_7\\ x_8\\ x_9\\ x_{10}\\ x_{11}\\ x_{12}\\ x_{13}\\ x_{14}\\ x_{15}\\ x_{16}\\ x_{17}\end{array}\right]$$$$Y=\left[\begin{array}{c}{y}_0\\ y_1\\ y_2\\ y_3\end{array}\right]$$我们再用矩阵运算来描述标准卷积运算，这里使用矩阵$C$ 来表示新的卷积核矩阵：$$Y=CX$$ 经过推导，我们可以得到这个稀疏矩阵$C$，它的尺寸为$4\times 16$：$$C=\left[\begin{array}{cccccccccccccccc}{w}_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}& 0& 0& 0& 0& 0\\ 0& w_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}& 0& 0& 0& 0\\ 0& 0& 0& 0& w_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}& 0\\ 0& 0& 0& 0& 0& w_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}\end{array}\right]$$ 这里，我们用 图4 为大家直观的展示一下上边的矩阵运算过程。

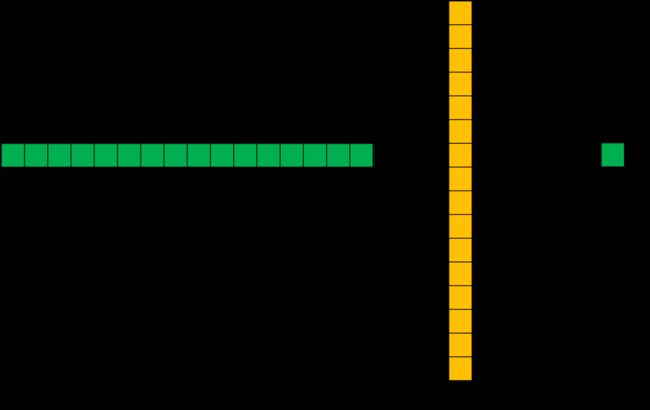
而转置卷积其实就是要对这个过程进行逆运算，即通过 C 和 Y 得到 X ：$$X=C^{T}Y$$ 此时，新的稀疏矩阵就变成了尺寸为$16\times 4$ 的$C^T$，这里我们通过下图为大家直观展示一下转置后的卷积矩阵运算示例。这里，用来进行转置卷积的权重矩阵不一定来自于原卷积矩阵. 只是权重矩阵的形状和转置后的卷积矩阵相同。

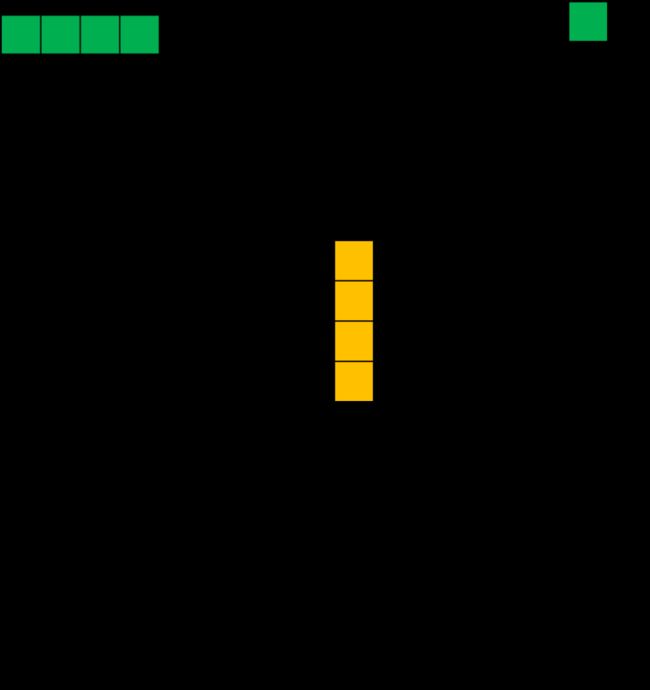
我们再将16×1 的输出结果进行重新排序，这样就可以通过尺寸为2×2 的输入矩阵得到尺寸为4×4 的输出矩阵了。

转置卷积输出特征图尺寸

stride=1的转置卷积

我们同样使用上文中的卷积核矩阵$C$：

$$C=\left[\begin{array}{cccccccccccccccc}{w}_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}& 0& 0& 0& 0& 0\\ 0& w_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}& 0& 0& 0& 0\\ 0& 0& 0& 0& w_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}& 0\\ 0& 0& 0& 0& 0& w_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}\end{array}\right]$$ 对应的输出矩阵 output 为 ：

$$output=\left[\begin{array}{cc}{y}_0& y_1\\ y_2& y_3\end{array}\right]$$ 我们将输出矩阵展开为列向量$Y$ ：$$Y=\left[\begin{array}{c}{y}_0\\ y_1\\ y_2\\ y_3\end{array}\right]$$ 带入到上文中提到的转置卷积计算公式，则转置卷积的计算结果为：$$C^T{y}^{\prime }=\left[\begin{array}{cccc}{w}_{0,0}{y}_0& w_{0,1}{y}_0+w_{0,0}{y}_1& w_{0,2}{y}_0+w_{0,1}{y}_1& w_{0,2}{y}_1\\ w_{1,0}{y}_0+w_{0,0}{y}_2& w_{1,1}{y}_0+w_{1,0}{y}_1+w_{0,1}{y}_2+w_{0,0}{y}_3& w_{1,2}{y}_0+w_{1,1}{y}_1+w_{0,2}{y}_2+w_{0,1}{y}_3& w_{1,2}{y}_1+w_{0,2}{y}_3\\ w_{2,0}{y}_0+w_{1,0}{y}_2& w_{2,1}{y}_0+w_{2,0}{y}_1+w_{1,1}{y}_2+w_{1,0}{y}_3& w_{2,2}{y}_0+w_{2,1}{y}_1+w_{1,2}{y}_2+w_{1,1}{y}_3& w_{2,2}{y}_1+w_{1,2}{y}_3\\ w_{2,0}{y}_2& w_{2,1}{y}_2+w_{2,0}{y}_3& w_{2,2}{y}_2+w_{2,1}{y}_3& w_{2,2}{y}_3\end{array}\right]$$ 这其实就等价于填充 padding=2，输入为：$$input=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& y_0& y_1& 0& 0\\ 0& 0& y_2& y_3& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$$ 同时，标准卷积核进行转置：

$$kerne{l}^{\prime }=\left[\begin{array}{ccc}{w}_{2,2}& w_{2,1}& w_{2,0}\\ w_{1,2}& w_{1,1}& w_{1,0}\\ w_{0,2}& w_{0,1}& w_{0,0}\end{array}\right]$$ 之后的标准卷积的结果，运算过程如下图所示：

对于卷积核尺寸为 k，步长 stride=1，填充 padding=0 的标准卷积，等价的转置卷积在尺寸为 $i^{\prime }$ 的输入矩阵上进行运算，输出特征图的尺寸 $o^{\prime }$ 为：$$o^{\prime }=i^{\prime }+(k-1)$$ 同时，转置卷积的输入矩阵需要进行 $paddin{g}^{\prime }=k-1$ 的填充。

stride>1的转置卷积

在实际使用的过程中，我们大多数时候使用的会是stride>1的转置卷积，从而获得较大的上采样倍率。这里，我们令输入尺寸为5×5，标准卷积核的设置同上，步长 stride=2，填充 padding=0，标准卷积运算后，输出尺寸为2×2。$$Y=\left[\begin{array}{c}{y}_0\\ y_1\\ y_2\\ y_3\end{array}\right]$$ 这里，步长$stride=2$，转换后的稀疏矩阵尺寸变为$25\times 4$，由于矩阵太大这里不展开进行罗列。则转置卷积的结果为：$$C^T{y}^{\prime }=\left[\begin{array}{ccccc}{w}_{0,0}{y}_0& w_{0,1}{y}_0& w_{0,2}{y}_0+w_{0,0}{y}_1& w_{0,1}{y}_1& w_{0,2}{y}_1\\ w_{1,0}{y}_0& w_{1,1}{y}_0& w_{1,2}{y}_0+w_{1,0}{y}_1& w_{1,1}{y}_1& w_{1,2}{y}_1\\ w_{2,0}{y}_0+w_{0,0}{y}_2& w_{2,1}{y}_0+w_{0,1}{y}_2& w_{2,2}{y}_0+w_{2,0}{y}_1+w_{0,2}{y}_2+w_{0,0}{y}_3& w_{2,1}{y}_1+w_{0,1}{y}_3& w_{2,2}{y}_1+w_{0,2}{y}_3\\ w_{1,0}{y}_2& w_{1,1}{y}_2& w_{1,2}{y}_2+w_{1,0}{y}_3& w_{1,1}{y}_3& w_{1,2}{y}_3\\ w_{2,0}{y}_2& w_{2,1}{y}_2& w_{2,2}{y}_2+w_{2,0}{y}_3& w_{2,1}{y}_3& w_{2,2}{y}_3\end{array}\right]$$ 此时，等价于输入矩阵添加了空洞，同时也添加了填充，标准卷积核进行转置之后的运算结果。运算过程如下图所示。

对于卷积核尺寸为 k，步长 stride>1，填充 padding=0 的标准卷积，等价的转置卷积在尺寸为 $i^{\prime }$ 的输入矩阵上进行运算，输出特征图的尺寸 $o^{\prime }$ 为：$$o^{\prime }=s(i^{\prime }-1)+k$$ 同时，转置卷积的输入矩阵需要进行 $paddin{g}^{\prime }=k-1$ 的填充，相邻元素间的空洞大小为 s−1。因此，可以通过控制步长 stride 来控制上采样倍率。

空洞卷积（Dilated Convolution）

空洞卷积提出背景

在像素级预测问题中（比如语义分割，这里以FCN为例进行说明），图像输入到网络中，FCN先如同传统的CNN网络一样对图像做卷积以及池化计算，降低特征图尺寸的同时增大感受野。但是由于图像分割是一种像素级的预测问题，因此我们使用转置卷积（Transpose Convolution）进行上采样使得输出图像的尺寸与原始的输入图像保持一致。综上，在这种像素级预测问题中，就有两个关键步骤：首先是使用卷积或者池化操作减小图像尺寸，增大感受野；其次是使用上采样扩大图像尺寸。但是，使用卷积或者池化操作进行下采样会导致一个非常严重的问题：图像细节信息被丢失，小物体信息将无法被重建(假设有4个步长为2的池化层，则任何小于 $2^4$pixel 的物体信息将理论上无法重建)。

空洞卷积及其应用

空洞卷积(Dilated Convolution)，在某些文献中也被称为扩张卷积（Atrous Deconvolution），是针对图像语义分割问题中下采样带来的图像分辨率降低、信息丢失问题而提出的一种新的卷积思路。空洞卷积通过引入扩张率（Dilation Rate）这一参数使得同样尺寸的卷积核获得更大的感受野。相应地，也可以使得在相同感受野大小的前提下，空洞卷积比普通卷积的参数量更少。

空洞卷积在某些特定的领域有着非常广泛的应用，比如：

• 语义分割领域：DeepLab系列与DUC。在DeepLab v3算法中，将ResNet最后几个block替换为空洞卷积，使得输出尺寸变大了很多。在没有增大运算量的前提下，维持分辨率不降低，获得了更密集的特征响应，从而使得还原到原图时细节更好。

• 目标检测领域：RFBNet。在RFBNet算法中，利用空洞卷积来模拟pRF在人类视觉皮层中的离心率的影响，设计了RFB模块，从而增强轻量级CNN网络的效果。提出基于RFB网络的检测器，通过用RFB替换SSD的顶部卷积层，带来了显著的性能增益，同时仍然保持受控的计算成本。

• 语音合成领域：WaveNet等算法。

空洞卷积与标准卷积的区别

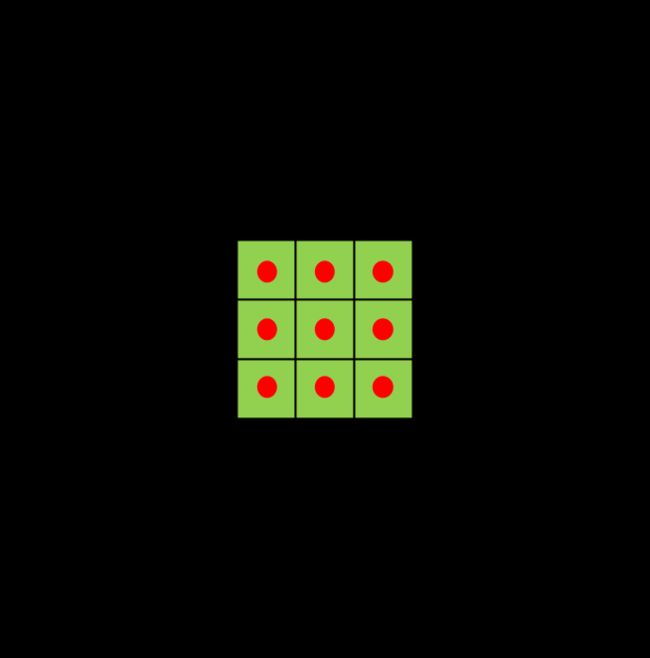
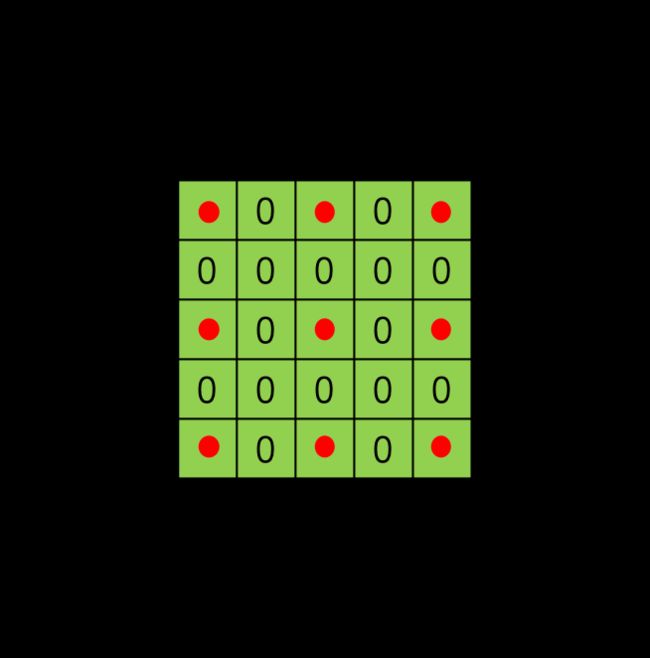
对于一个尺寸为 3×3 的标准卷积，卷积核大小为 3×3 ，卷积核上共包含9个参数，在卷积计算时，卷积核中的元素会与输入矩阵上对应位置的元素进行逐像素的乘积并求和。而空洞卷积与标准卷积相比，多了扩张率这一个参数，扩张率控制了卷积核中相邻元素间的距离，扩张率的改变可以控制卷积核感受野的大小。尺寸为 3×3 ，扩张率分别为 1,2,4 时的空洞卷积分别如下图所示。

扩张率为1时，空洞卷积与标准卷积计算方式一样。

扩张率为2时的3*3空洞卷积。

扩张率为4时的3*3空洞卷积。扩张率大于1时，在标准卷积的基础上，会注入空洞，空洞中的数值全部填0。

空洞卷积的感受野

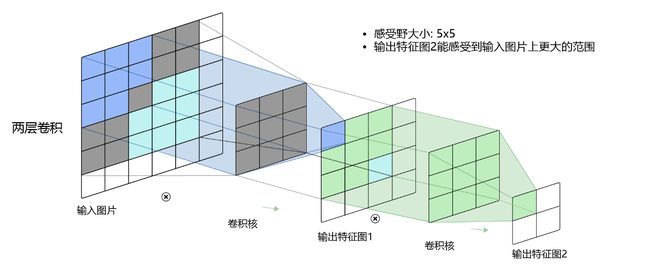
对于标准卷积而言，当标准卷积核尺寸为 3×3 时，我们在输入矩阵上连续进行两次标准卷积计算，得到两个特征图。我们可以观察不同层数的卷积核感受野大小，如下图所示：

其中，$3\times 3$卷积对应的感受野大小就是$3\times 3$，而通过两层$3\times 3$的卷积之后，感受野的大小将会增加到$5\times 5$。

空洞卷积的感受野计算方式与标准卷积大同小异。由于空洞卷积实际上可以看作在标准卷积核内填充’0’，所以我们可以将其想象为一个尺寸变大的标准卷积核，从而使用标准卷积核计算感受野的方式来计算空洞卷积的感受野大小。对于卷积核大小为 k ，扩张率为 r 的空洞卷积，感受野 F 的计算公式为：$$F=k+(k-1)(r-1)$$卷积核大小 k=3 ，扩张率 r=2 时，计算方式如下图所示。

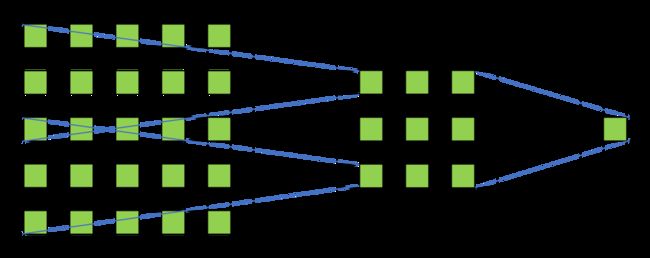
其中，通过一层空洞卷积后，感受野大小为5×5，而通过两层空洞卷积后，感受野的大小将会增加到9×9。

分组卷积（Group Convolution）

分组卷积提出背景

分组卷积（Group Convolution）最早出现在AlexNet中。受限于当时的硬件资源，在AlexNet网络训练时，难以把整个网络全部放在一个GPU中进行训练，因此，作者将卷积运算分给多个GPU分别进行计算，最终把多个GPU的结果进行融合。因此分组卷积的概念应运而生。

分组卷积与标准卷积的区别

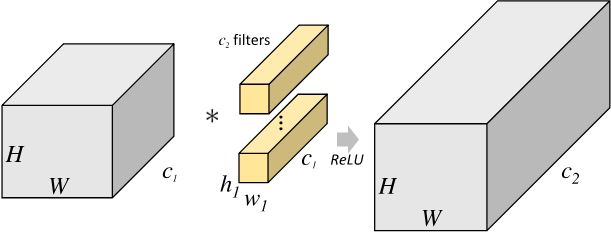
对于尺寸为 $H_1\times W_1\times C_1$ 的输入矩阵，当标准卷积核的尺寸为 $h_1\times w_1\times C_1$ ，共有 $C_2$ 个标准卷积核时，标准卷积会对完整的输入数据进行运算，最终得到的输出矩阵尺寸为 $H_2\times W_2\times C_2$ 。这里我们假设卷积运算前后的特征图尺寸保持不变，则上述过程可以展示为下图。

考虑到上述过程是完整运行在同一个设备上，这也对设备的性能提出了较高的要求。

分组卷积则是针对这一过程进行了改进。分组卷积中，通过指定组数 $g$ 来确定分组数量，将输入数据分成 $g$ 组。需要注意的是，这里的分组指的是在深度上进行分组，输入的宽和高保持不变，即将每 $\frac{C_1}{g}$ 个通道的数据分为一组。因为输入数据发生了改变，相应的卷积核也需要进行对应的变化，即每个卷积核的输入通道数也就变为了 $\frac{C_1}{g}$ ，而卷积核的大小是不需要改变的。同时，每组的卷积核个数也由原来的 $C_2$ 变为 $\frac{C_2}{g}$ 。对于每个组内的卷积运算，同样采用标准卷积运算的计算方式，这样就可以得到 $g$ 组尺寸为 $H_2\times W_2\times \frac{C_2}{g}$ 的输出矩阵，最终将这 $g$ 组输出矩阵进行拼接就可以得到最终的结果。这样拼接完成后，最终的输出尺寸就可以保持不变，仍然是 $H_2\times W_2\times C_2$ 。分组卷积的运算过程如下图所示。

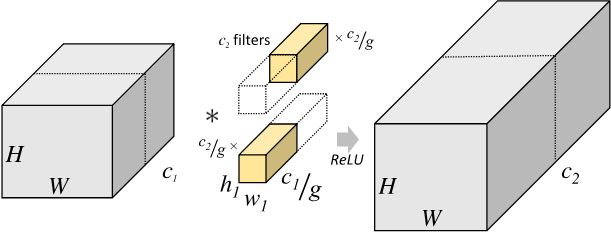
由于我们将整个标准卷积过程拆分成了 g 组规模更小的子运算来并行进行，所以最终降低了对运行设备的要求。同时，通过分组卷积的方式，参数量也可以得到降低。在上述的标准卷积中，参数量为：$$h_1\times w_1\times C_1\times C_2$$ 而使用分组卷积后，参数量则变为：$$h_1\times w_1\times \frac{C_1}{g}\times \frac{C_2}{g}\times g=h_1\times w_1\times C_1\times C_2\times \frac{1}{g}$$

应用示例

比如对于尺寸为 $H\times W\times 64$ 的输入矩阵，当标准卷积核的尺寸为 $3\times 3\times 64$ ，共有 64 个标准卷积核时，下图为组数 g=2 时的分组卷积计算方式。

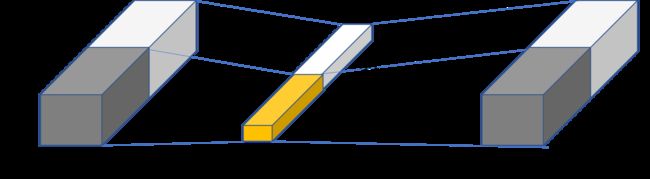
此时，每组的输入通道数变为32，卷积核通道数也变为为32。所以，标准卷积对应的参数量是 3×3×64×64=36864 ，而分组卷积的参数量变为 3×3×32×32×2=18432，参数量减少了一半。