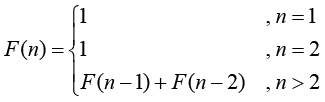神奇的兔子数列
14天阅读挑战赛
文章目录
- 概览
- 前言
- 导读
- 兔子案例
-
-
- 兔子的繁殖过程
- 发现规律
- 设计计算
-
- 简单循环
- 解构赋值
- 通项公式
-
- 结束语
概览
- ✨ 食用时间: 10分钟
- ✨ 难度: 「简单」,别跑,看完再走
- ✨ 食用价值:斐波那契数列
- ✨ 铺垫知识: JavaScript
前言
努力是为了不平庸~
算法学习有些时候是枯燥的,这一次,让我们先人一步,趣学算法!欢迎记录下你的那些努力时刻(算法学习知识点/算法题解/遇到的算法bug/等等),在分享的同时加深对于算法的理解,同时吸收他人的奇思妙想,一起见证技术er的成长~
导读
假设第1个月有1对初生的兔子,第2个月进入成熟期,第3个月开始生育兔子,而1对成熟的兔子每月会生1对兔子,兔子永不死去……那么,由1对初生的兔子开始,12个月后会有多少对兔子呢?
兔子数列即 斐波那契数列 ,它的发明者是意大利数学家莱奥纳尔多·斐波那契(Leonardo Fibonacci,1170—1250)。1202年,莱奥纳尔多撰写了《算盘全书》(Liber Abaci),该书是一部较全面的初等数学著作。书中系统地介绍了印度—阿拉伯数码及其演算法则,以及中国的“盈不足术”;此外还引入了负数,并研究了一些简单的一次同余式组。
兔子案例
- 第1个月,小兔子①没有繁殖能力,所以还是1对。
- 第2个月,小兔子①进入成熟期,仍然是1对。
- 第3个月,兔子①生了1对小兔子②,于是这个月共有2(1+1=2)对兔子。
- 第4个月,兔子①又生了1对小兔子③,因此共有3(1+2=3)对兔子。
- 第5个月,兔子①又生了1对小兔子④,而在第3个月出生的兔子②也生下了1对小兔子⑤,因此共有5(2+3=5)对兔子。
- 第6个月,兔子①②③各生下了1对小兔子,新生的3对兔子加上原有的5对兔子,这个月共有8(3+5=8)对兔子。
- … … …
兔子的繁殖过程
发现规律
这个数列有如下十分明显的特点:从第3个月开始,当月的兔子数=上月兔子数+当月新生兔子数,而当月新生兔子数正好等于上上月的兔子数。因此,前面相邻两项之和便构成后一项,换言之:
当月的兔子数 = 上月兔子数 + 上上月的兔子数
斐波那契数列如下:
1,1,2,3,5,8,13,21,34,…
递归表达式如下:
设计计算
简单循环
打印前20行
function fn() {
const fi = []; //---1
fi[1] = 1; //---2
fi[2] = 1; //---3
for (let i = 3; i < 20; i++) {
fi[i] = fi[i - 1] + fi[i - 2]; //---4
}
for (let i = 0; i < fi.length; i++) { //---5
console.log(fi[i]); //---6
}
}
- 在行{1}处,我们声明并创建了一个数组。
- 在行{2}和行{3},把斐波那契数列中的前两个数分别赋给了数组的第二和第三个位置。(在JavaScript中,数组第一位的索引始终是0。因为斐波那契数列中不存在0,所以这里直接略过,从第二位开始分别保存斐波那契数列中对应位置的元素。)
- 然后,我们需要做的就是想办法得到斐波那契数列中第三到第二十个位置上的数(前两个值我们已经初始化过了)。我们可以用循环来处理,把数组中前两位上的元素相加,结果赋给当前位置上的元素(行{4}——从数组中的索引3到索引19)。
- 最后,看看输出(行{6}),我们只需要循环迭代数组的各个元素(行{5})。
解构赋值
function fibonacci(n) {
let current = 1;
let next = 1;
for(let i = 0; i < n; i++){
[current, next] = [next, current + next];
}
return current;
}
通项公式
function fibonacci(n) {
const SQRT_FIVE = Math.sqrt(5);
return Math.round(1/SQRT_FIVE * (Math.pow(0.5 + SQRT_FIVE/2, n) - Math.pow(0.5 - SQRT_FIVE/2, n)));
}
结束语
希望本文对你有一点点帮助,如果有用请点个赞吧 ~