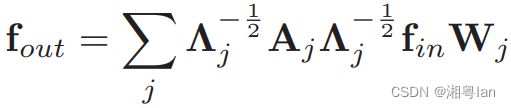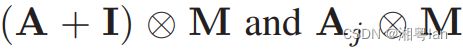论文超详细精读|六千字:ST-GCN
文章目录
- 前言
- 总览
- 一、Introduction
-
- 背景与局限
- 解决问题思路
- 新方法及主要贡献
- 二、Related work
-
- Neural Networks on Graphs(图神经网络)
- Skeleton Based Action Recognition(基于骨骼的动作识别)
- 三、Spatial Temporal Graph ConvNet(时空图卷积网络)
-
- 3.1 Pipeline Overview (网络架构)
- 3.2 Skeleton Graph Construction(骨架图的构建)
- 3.3 Spatial Graph Convolutional Neural Network(空间图卷积神经网络)
- 3.4 Partition Strategies(分区策略)
- 3.5 Learnable edge importance weighting(可学边界权重)
- 3.6 Implementing ST-GCN
-
- 小白知识
- 原文实现

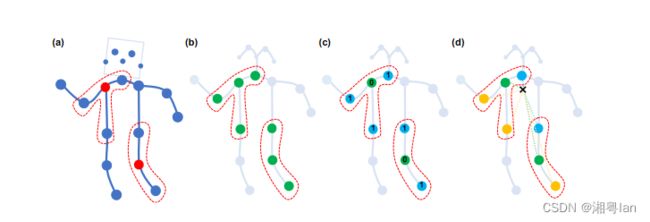
蓝点表示身体的关节。帧间边缘连接连续帧之间的相同节点。关节坐标被用作ST-GCN的输入。
前言
笔者从人工智能小白的角度,力求能够从原文中解析出最高效率的知识。
之前看了很多博客去学习AI,但发现虽然有时候会感觉很省时间,但到了复现的时候就会傻眼,因为太多实现的细节没有提及。而且博客具有很强的主观性,因此我建议还是搭配原文来看。
请下载原文《Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition》搭配阅读本文,会更高效哦!
总览
首先,看完标题,摘要和结论,我了解到了以下信息:
- 提出了一个新的动态骨架模型,称为时空图卷积网络(ST-GCN),它通过自动从数据中学习空间和时间模式,传统的骨骼建模方法通常依赖于手工制作的部件或遍历规则,从而导致表达能力有限和泛化困难,ST-GCN则超越了以前方法的局限性。该公式不仅具有较强的表达能力,而且具有较强的泛化能力。
- 此外,ST-GCN可以捕获动态骨架序列中的运动信息,这是对RGB模态的补充。基于骨架模型和基于框架模型的结合进一步提高了动作识别的性能。
一、Introduction
背景与局限
1.动态骨骼形态可以用人类关节位置的时间序列来表示,以2D或3D坐标的形式。然后,通过分析人类的运动模式,可以识别人类的行为。
2.早期使用骨骼进行动作识别的方法简单地利用单个时间步的关节坐标形成特征向量,并对其进行时间分析,这些方法的能力是有限的,因为它们没有明确地利用关节之间的空间关系,这是理解人类行为的关键。
3.现有的方法大多依赖于手工制作的部件或规则来分析空间模式。因此,针对特定应用设计的模型很难推广到其他应用。
解决问题思路
1.神经网络解决自动问题。为了超越这些限制,我们需要一种新的方法,能够自动捕获嵌入关节空间配置中的模式以及它们的时间动态。然而,骨架是图形形式的,而不是2D或3D网格,这使得使用卷积网络等经过验证的模型变得困难。
2.图神经网络解决卷积对象非图像问题。Graph Neural networks (GCNs)是一种将卷积神经网络(CNNs)推广到任意结构图的方法,但需要固定的图作为输入。
3.通过将图神经网络扩展到一个时空图模型,即时空图卷积网络(ST-GCN),设计一种用于动作识别的骨架序列的通用表示。
新方法及主要贡献
- 有两种类型的边,即符合关节自然连通性的空间边和跨越连续时间步长的连接相同关节的时间边。在此基础上构造了多层时空图卷积,实现了信息在空间维度和时间维度上的集成。
- 主要贡献在于三个方面:
(1)提出了一种基于图的动态骨骼建模通用公式ST-GCN,这是第一个将基于图的神经网络应用于该任务的方法。
(2)针对骨骼建模的具体要求,提出了ST-GCN中卷积核的设计原则。
(3)在基于骨骼的动作识别的两个大规模数据集上,与使用手工制作部件或遍历规则的方法相比,所提模型在手工设计方面的工作量大大减少,取得了更好的性能。
二、Related work
Neural Networks on Graphs(图神经网络)
两种思路:
1.光谱视角,以光谱分析的形式考虑图卷积的局部性。
2.空间视角,其中卷积滤波器(filter)直接应用于图节点及其周边点。
本文选了第二种思路。在空间域上构建CNN滤波器,将每个滤波器的应用限制在每个节点的1个邻居节点。
Skeleton Based Action Recognition(基于骨骼的动作识别)
人体的骨骼和关节轨迹对光照变化和场景变化具有鲁棒性,通过高度精确的深度传感器或位姿估计算法很容易获得。因此,这里有一系列基于骨架的动作识别方法。这些方法可以分为基于特征的人工方法和深度学习方法。第一种方法设计了几个人工特征来捕捉关节运动的动态。
三、Spatial Temporal Graph ConvNet(时空图卷积网络)
在图像目标识别等任务中,层次化表示和局部性通常是利用卷积神经网络的固有性质来实现的。
3.1 Pipeline Overview (网络架构)
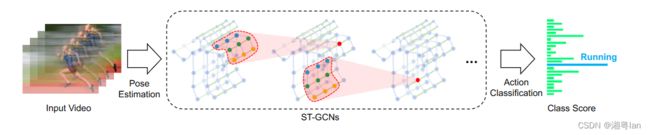
1.数据来源:从运动捕获设备或从视频中的姿势估计算法获得
2.输入:图形节点上的关节坐标向量。通常数据是一系列的帧,每个帧都会有一组关节坐标。这可以被认为是对基于图像的CNN的模拟。将对输入数据进行多层时空图形卷积运算,并在图形上生成更高级别的要素地图。
3.输出:然后,标准SoftMax分类器将其分类到相应的操作类别。
4.训练方式:整个模型采用端到端的反向传播方式进行训练。
3.2 Skeleton Graph Construction(骨架图的构建)
骨架序列通常由每个帧中每个人体关节的2D或3D坐标表示。以前的工作使用卷积来识别骨骼动作,将所有关节的坐标向量连接在一起,形成每帧的单个特征向量。本文利用时空图来形成骨架序列的层次表示,在具有 N N N 个关节和 T T T 个帧的骨架序列上构造了一个无向时空图 G = ( V , E ) G=(V,E) G=(V,E) ,该图既具有体内连接又具有帧间连接。具体表示如下:
- 骨架序列关节: V = { v t i ∣ t = 1 , . . . , T , i = 1 , . . . , N } V =\{v_{ti}|t = 1, . . . , T, i = 1, . . . , N\} V={vti∣t=1,...,T,i=1,...,N} 作为ST-GCN的输入,节点 F ( v t i ) F(v_{ti}) F(vti) 上的特征向量由帧 t t t 上第 i i i 个关节的坐标向量和估计置信度组成。
- 构建过程:
(1)根据人体结构的连通性,将一个框架内的关节用边连接起来,如图1所示。
(2)将每个关节连接到连续帧中的同一关节。因此,此设置中的连接是自然定义的,不需要人工来手动配置。这还使网络体系结构能够处理具有不同连接数或连接性的数据集。 - 边集 E E E 由两个子集组成:
(1) E S = { v t i v t j ∣ ( i , j ) ∈ H } E_S=\{v_{ti}v_{tj}|(i,j)∈H\} ES={vtivtj∣(i,j)∈H},其中 H H H 是自然连接的人体关节的集合。第一个子集描述了每一帧的骨架内连接。
(2) E F = { v t i v ( t + 1 ) i } E_F=\{v_{ti}v_{(t+1)i}\} EF={vtiv(t+1)i},第二个子集包含帧间边,这些边将连续帧中的相同关节连接。因此,一个特定关节 I I I的 E F E_F EF中的所有边都将表示其随时间变化的轨迹。
3.3 Spatial Graph Convolutional Neural Network(空间图卷积神经网络)
1.单个帧情况: 帧 T T T 上,有 N N N 个关节节点 V t V_t Vt ,以及骨架边 E S = { v t i v t j ∣ ( i , j ) ∈ H } E_S=\{v_{ti}v_{tj}|(i,j)∈H\} ES={vtivtj∣(i,j)∈H},它们都可以被视为2D网络,卷积运算的输出特侦图也是2D网络。步长设置为1,选择合适的padding,输出特征映射可以具有与输入特征映射相同的大小。
2.空间位置x处的单个通道输出值:
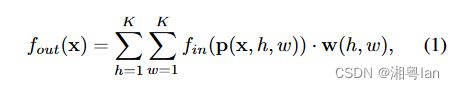
其中,
(1)采样函数 p : Z 2 × Z 2 → Z 2 p:Z^2 \times Z^2\rightarrow Z^2 p:Z2×Z2→Z2 枚举了位置x的邻居节点。
(2)权重函数 w : Z 2 → R c w:Z^2\rightarrow\mathbb{R^c} w:Z2→Rc 提供 c c c 维实空间中的权重向量,用于计算具有 c c c 维的采样输入特征向量的内积。
**注意,权重函数与输入位置x无关。因此,在输入图像上均共享滤波器权重。**
然后,通过将上述公式扩展到输入特征图驻留在空间图 V t V_t Vt 上的情况来定义图上的卷积运算。也就是说:特征图 f i n t : V t → R c f_{in}^t : V_t→R^c fint:Vt→Rc 中的特征映射在图形的每个节点上都有一个向量。扩展的下一步是重新定义采样函数 p p p 和权重函数 w w w 。
3.4 Partition Strategies(分区策略)
- Uni-labeling:
这种方法是对该中心节点及其邻近节点採用等价的权重计算,算是最简单、直接的做法。 - Distance partitioning:
这方法是依照中心节点 ( Root ) 到其他节点的距离做加权,而中心节点的权重会设定为 0。 - Spatial configuration partitioning:
这方法比较特别,会依空间上的相对关系进行分 3 群的动作,这 3 群分别是 Root 、向心群、离心群,这边的向心离心的判定是以所有节点的重心做判断 ( 可参考上图 d 的图示,打叉的地方就是重心,绿色的是 Root ,蓝色是向心群,黄色是离心群 )
上述 3 点的图示可依序对应到上图的 (b)、(c)、(d):
从左到右:
(a):输入骨架的示例帧。身体关节用蓝色圆点绘制。D=1的过滤器的接受域用红色虚线圆圈绘制。
(b):单标签划分策略,其中一个邻域中的所有节点都有相同的标签(绿色)。
(c):距离划分。这两个子集是距离为0(绿色)的根节点本身和距离为1(蓝色)的其他邻接点。
(d):空间构型划分。节点根据其到骨骼重心的距离(黑色十字)与根节点的距离(绿色)进行标记。向心节点的距离较短(蓝色),而离心式节点的距离较长(黄色)。
3.5 Learnable edge importance weighting(可学边界权重)
尽管当人们执行动作时,关节会成组移动,但一个关节可能会出现在身体的多个部位。进行建模时应该具有不同的重要性。在这个意义上,本文在时空图卷积的每一层都增加了一个可学习的掩码M。掩码将基于 E S E_S ES中每条空间图边的学习重要性权重来缩放节点特征对其相邻节点的贡献。实验发现,加入这种掩码可以进一步提高ST-GCN的识别性能。
3.6 Implementing ST-GCN
小白知识
普通图像的二维卷积,他可以看成: X ∗ = X W + b X^*=XW+b X∗=XW+b。
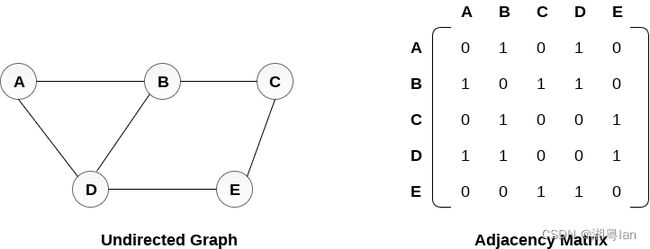
图卷积可以看成: X ∗ = A X W + b X^*=AXW+b X∗=AXW+b,多左乘了一个邻接矩阵A。邻接矩阵就是他的行和列都是点,而点与点有没有连接用对应矩阵的元素表示,1就代表有连接,0就代表没有连接。这篇论文用的是无向图。简单来说邻接矩阵就是描述点与边有无联系的一个矩阵。
原文实现
在实作上,这些 Graph 的 Edge 会以 Adjacency matrix A 做重现,而每个节点对应自己的重现方法则以 Identity matrix I 实作,而前面Partition Strategies 里的第一种方法则可表述为:
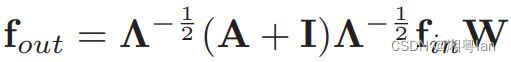
Λ i i = ∑ j ( A i j + I i j ) Λ^{ii} = ∑_j(A^{ij} + I^{ij}) Λii=∑j(Aij+Iij), W W W 是进行加权的矩阵。
而在 ST-GCN 的实作上,会同时对时空的维度上进行特徵抽取的操作,所以输入的特征图维度会是 ( C , V , T C, V, T C,V,T )。
另外 2 种 Partition Strategies 因为有 Subset ,在 Adjacency matrix 的数量上上就比较多,也可以把上个公式的 A + I A + I A+I 拆解来看:

若以 Distance partitioning 为例, A j A_j Aj可表述为:
![]()
而前面提到过可训练的 Mask M,在这边会加在 A + I A + I A+I 或 A j A_j Aj 后方: