河北工业大学数据挖掘实验五
k-均值聚类算法
- 一、实验目的
- 二、实验原理
-
- 1、k-均值聚类
- 2、终止条件
- 三、实验内容和步骤
-
- 1、实验内容
- 2、实验步骤
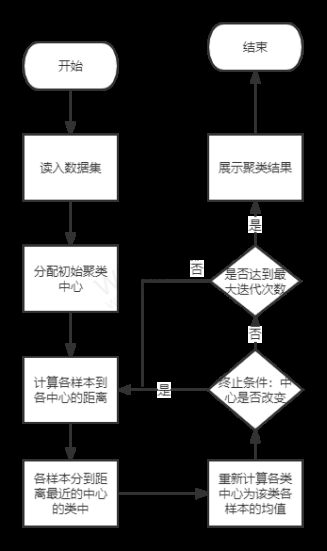
- 3、程序框图
- 4、实验样本
- 5、实验代码
- 四、实验结果
- 五、实验分析
一、实验目的
- 熟悉k-均值聚类算法。
- 在训练样本集上编写用于 k-均值聚类的程序,对任务相关数据运行 k-均值聚类算法,调试实验。
- 掌握距离计算方法和聚类的评价准则。
- 写出实验报告。
二、实验原理
1、k-均值聚类
k-均值聚类是一种基于形心的划分技术,具体迭代的计算步骤如下:
- 在属性向量空间随机产生k个形心坐标。
- 分别计算数据集 D 中的每个数据对象 T i ( 1 ≤ i ≤ n ) T_i (1\leq i\leq n) Ti(1≤i≤n)到所有 k k k个形心的距离度量 D i s t ( i , j ) ( 1 ≤ i ≤ n , 1 ≤ j ≤ k ) Dist(i,j) (1\leq i\leq n, 1\leq j\leq k) Dist(i,j)(1≤i≤n,1≤j≤k),并将数据对象 T i T_i Ti 聚到最小距离度量的那一簇中。即 T i ∈ C J T_i\in C_J Ti∈CJ,表示数据对象 T i T_i Ti被聚到第 J J J簇中。其中 J = arg min ( D i s t ( i , j ) ) J=\argmin(Dist(i,j)) J=argmin(Dist(i,j)),表示 J J J为可使得 D i s t ( i , j ) Dist(i,j) Dist(i,j)取最小值的那个 j j j。
- 按照形心的定义计算每一簇的形心坐标,形成下一代的 k k k个形心坐标。
- 如果不满足终结条件,转到 2)继续迭代;否则结束。
其中,簇的形心可以有不同的的定义,例如可以是簇内数据对象属性向量的均值(也就是重心),也可以是中心点等;距离度量也可以有不同的定义,常用的有欧氏距离、曼哈顿(或城市块、街区)距离、闵可夫斯基距离等;终结条件可采用当对象的重新分配不再发生时,程序迭代结束。
2、终止条件
终止条件可以是以下任何一个:
- 没有(或最小数目)对象被重新分配给不同的聚类。
- 没有(或最小数目)聚类中心再发生变化。
- 误差平方和局部最小。
三、实验内容和步骤
1、实验内容
- 根据 k-均值聚类算法的计算步骤,画出 k=3 时的程序流程图;
- 由 k-均值程序流程图编程实现 k-均值聚类算法;
- 在实验报告中显示 k-均值聚类过程的一系列截图,指明各个簇的逐渐演
化过程; - 在报告中指出实验代码中的初始质心的选择,终止条件的选择,以及距
离度量的选择并予以说明。
2、实验步骤
编程实现如下功能:
- 首先将数据集 D={D1,D2,D3}中的属性向量作为实验数据输入;
- 由 k-均值程序流程图编程实现 k-均值聚类算法,并用实验数据运行;
- 运行过程中在适当的迭代代数暂停并显示实时迭代的结果,如簇心的位
置、按距离最近邻聚类的结果等;
3、程序框图
4、实验样本
data.txt
5、实验代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
#
# Copyright (C) 2021 #
# @Time : 2022/5/30 21:29
# @Author : Yang Haoyuan
# @Email : [email protected]
# @File : Exp5.py
# @Software: PyCharm
import math
import random
import argparse
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import calinski_harabasz_score
parser = argparse.ArgumentParser(description="Exp5")
parser.add_argument("--epochs", type=int, default=100)
parser.add_argument("--k", type=int, default=3)
parser.add_argument("--n", type=int, default=2)
parser.add_argument("--dataset", type=str, default="data.txt")
parser.set_defaults(augment=True)
args = parser.parse_args()
print(args)
# 读取数据集
def loadDataset(filename):
dataSet = []
with open(filename, 'r') as file_to_read:
while True:
lines = file_to_read.readline() # 整行读取数据
if not lines:
break
p_tmp = [str(i) for i in lines.split(sep="\t")]
p_tmp[len(p_tmp) - 1] = p_tmp[len(p_tmp) - 1].strip("\n")
for i in range(len(p_tmp)):
p_tmp[i] = float(p_tmp[i])
dataSet.append(p_tmp)
return dataSet
# 计算n维数据间的欧式距离
def euclid(p1, p2, n):
distance = 0
for i in range(n):
distance = distance + (p1[i] - p2[i]) ** 2
return math.sqrt(distance)
# 初始化聚类中心
def init_centroids(dataSet, k, n):
_min = dataSet.min(axis=0)
_max = dataSet.max(axis=0)
centre = np.empty((k, n))
for i in range(k):
for j in range(n):
centre[i][j] = random.uniform(_min[j], _max[j])
return centre
# 计算每个数据到每个中心点的欧式距离
def cal_distance(dataSet, centroids, k, n):
dis = np.empty((len(dataSet), k))
for i in range(len(dataSet)):
for j in range(k):
dis[i][j] = euclid(dataSet[i], centroids[j], n)
return dis
# K-Means聚类
def KMeans_Cluster(dataSet, k, n, epochs):
epoch = 0
# 初始化聚类中心
centroids = init_centroids(dataSet, k, n)
# 迭代最多epochs
while epoch < epochs:
# 计算欧式距离
distance = cal_distance(dataSet, centroids, k, n)
classify = []
for i in range(k):
classify.append([])
# 比较距离并分类
for i in range(len(dataSet)):
List = distance[i].tolist()
# 因为初始中心的选取完全随机,所以存在第一次分类,类的数量不足k的情况
# 这里作为异常捕获,也就是distance[i]=nan的时候,证明类的数量不足
# 则再次递归聚类,直到正常为止,返回聚类标签和中心点
try:
index = List.index(distance[i].min())
except:
labels, centroids = KMeans_Cluster(dataSet=np.array(data_set), k=args.k, n=args.n, epochs=args.epochs)
return labels, centroids
classify[index].append(i)
# 构造新的中心点
new_centroids = np.empty((k, n))
for i in range(len(classify)):
for j in range(n):
new_centroids[i][j] = np.sum(dataSet[classify[i]][:, j:j + 1]) / len(classify[i])
# 比较新的中心点和旧的中心点是否一样
if (new_centroids == centroids).all():
# 中心点一样,停止迭代
label_pred = np.empty(len(data_set))
# 返回个样本聚类结果和中心点
for i in range(k):
label_pred[classify[i]] = i
return label_pred, centroids
else:
centroids = new_centroids
epoch = epoch + 1
# 聚类结果展示
def show(label_pred, X, centroids):
x = []
for i in range(args.k):
x.append([])
for k in range(args.k):
for i in range(len(label_pred)):
_l = int(label_pred[i])
x[_l].append(X[i])
for i in range(args.k):
plt.scatter(np.array(x[i])[:, 0], np.array(x[i])[:, 1], color=plt.cm.Set1(i % 8), label='label' + str(i))
plt.scatter(x=centroids[:, 0], y=centroids[:, 1], marker='*', label='pred_center')
plt.legend(loc=3)
plt.show()
if __name__ == "__main__":
# 读取数据
data_set = loadDataset(args.dataset)
# 原始数据展示
plt.scatter(np.array(data_set)[:, :1], np.array(data_set)[:, 1:])
plt.show()
# 获取聚类结果
labels, centroids = KMeans_Cluster(dataSet=np.array(data_set), k=args.k, n=args.n, epochs=args.epochs)
print("Classes: ", labels)
print("Centers: ", centroids)
# 使用Calinski-Harabaz标准评价聚类结果
scores = calinski_harabasz_score(data_set, labels)
print("Scores: ", round(scores, 2))
# 展示聚类结果
show(X=np.array(data_set), label_pred=labels, centroids=centroids)
四、实验结果
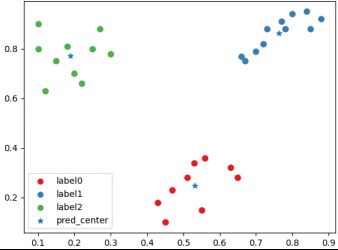
一种“好”聚类后分类情况散点图以及聚类中心

一种“好”聚类后聚类标签,聚类中心和CH指数得分情况
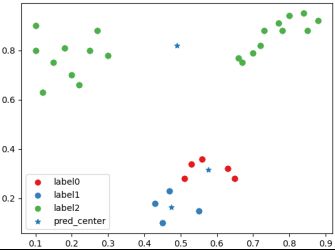
一种“坏”聚类后分类情况散点图以及聚类中心

一种“坏”聚类后聚类标签,聚类中心和CH指数得分情况
五、实验分析
本次实验主要是K-Means算法的实现。
对于样本之间的距离,我采用欧几里得距离度量,这是在经典K-Means算法中已经被证明是高度有效的相似性和非相似性度量标准。
我将聚类中心不再变化或者迭代次数达到上限作为终止条件,放着某些不收敛的情况造成的程序运行时间过长。
由于聚类中心的初始选取完全随机,所以可能出现第一次聚类类的数量小于规定的k的情况,对于这种情况,我在异常处理中直接进行递归,重新开始聚类,返回递归聚类结果。同时,由于聚类中心的随机性,即使针对同一数据集,在参数相同的情况下,其聚类结果有可能存在巨大差距。为了评判聚类结果的“好”或“坏”,我使用 C a l i n s k i − H a r a b a z ( C H ) Calinski-Harabaz(CH) Calinski−Harabaz(CH)标准评价聚类结果。这是一种经典的算法,用以评价类间和类内部的协方差,进而评价聚类结果。较之于Silhouettes指数,CH指数的计算更加快捷。其计算公式如下:
C H = B G S S k − 1 / W G S S n − k CH=\frac{BGSS}{k-1} / \frac{WGSS}{n-k} CH=k−1BGSS/n−kWGSS
BGSS指类间协方差,WGSS指类内协方差。一个好的聚类应当具有较大的类间协方差和较小的类内协方差,从而使得CH指数达到局部或者全局的最大值。从实验结果可以看出,在经验上更好的聚类结果确实具有更大的CH得分。