[Project Euler]加入欧拉 Problem 15

Starting in the top left corner of a 22 grid, there are 6 routes (without backtracking) to the bottom right corner.

How many routes are there through a 2020 grid?

 

从 2*2的一个角到达另外一个对角有6条线路，问从 20*20的一个角到达另外一个对角有多少条线路？

 

这个要是运用组合数学的知识就好解决了。下面是组合数学的一个东东：

下面是一个别人的东西，看下就和这个问题一样了。

 

小虫路线计数(I)

版权声明：转载时请以超链接形式标明文章原始出处和作者信息及本声明
http://yjq24.blogbus.com/logs/51125414.html

大家将就看~（我发现我很有鼠绘天赋阿），以后尽量多鼠绘~

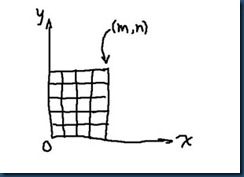
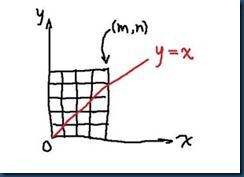
现在有个虫子在(0,0)，每步只能往x,y的正方向走，要求走到(m,n)，问有多少种路径（有一步不同的路径就视作不同的路径）。

这 玩意高中肯定都做过，因为每步只能走正方向，所以小虫不管怎么走，一共都是走m+n步到(m,n)，而这m+n步里，必然是m步向右，n步向上，所以说只 要从m+n步里选出其中的某m步，规定其向右走就行了。当然，你从中选出n步，规定其向上，得到的答案也是一样的。答数是 C(m+n,m)=C(m+n,n)。

 

看完就知道了答案了，就是 40! / (20! * 20!)

欧拉项目第十五道题#include <stdio.h>

#include <stdlib.h>



double JieChen(int n);



int main(int argc, char *argv[])

{

  double num1, num2, num3;

  

  num1 = JieChen(40);

  num2 = JieChen(20);

  num3 = num1 / (num2 * num2);  

  

  printf("%lf", num3);  

  system("PAUSE");	

  return 0;

}



double JieChen(int n)

{

    if(n == 1)

    return 1;

    else

    return n * JieChen(n - 1);

}

这题如果不利用组合数学的这个知识，还是挺费劲的，这个以后再想了。