python移动窗口求股票预测误差均值
目录
一、题目描述
二、题目分析
三、题目代码
四、总结
一、题目描述
已知贵州茅台的2019年1月至今每天的股票收益率序列(数据见下),采用移动窗口平均法预测,计算预测误差均值。并在[2,20]范围内求使得该误差最小的移动窗口长度。
移动窗口平均法预测的计算方法说明如下:
原始序列:0.3,0.1,0.5,0.4,0.6,0.3,0.6,0.8,0.3,0.2
当窗口长度=3时,步骤如下:
- 对0.3,0.1,0.5求平均得到0.3,作为第四天的预测值,该预测值与真实值的误差为:|0.4-0.3|=0.1
- 在原始序列上移动一个位置,即求0.1,0.5,0.4的平均值得到0.33作为第五天的预测值,误差为:|0.6-0.33|=0.27
- 继续往右移动一个位置,求0.5,0.4,0.6的平均值0.5作为第六天的预测值,误差为|0.3-0.5|=0.2
- 以此类推,直到0.6,0.8,0.3,误差为|0.2-0.57|=0.37把各个步骤的误差求平均得到预测误差均值。
股票的原始为:
num_list = [0.02931,0.048,0.0076,0.00302,
0.03759,-0.0058,-0.02738,0.00462,
0.00832,0.01201,-0.0095,0.01106,
-0.00728,0.02506,-0.00293,0.04029,
0,0.01134,0.00503,-0.00528,0.01363,
-0.00804,-0.02041,-0.00417,0.01918,
0.02333,-0.01979,0.00668,0.03198,0.04399,
-0.01258,-0.01274,-0.01649,-0.03191,0.0029,
0.03213,-0.02398,0.01543,0.0251,0.00361,0.03107,
-0.01619,-0.00253,0.00028,-0.00282,-0.00763,0.00128,
0.01592,0.05239,0.02994,-0.00001,-0.0231,-0.00014,
0.07143,0.00333,0,0.04983,-0.04114,0.0242,-0.02803,
0.03658,0.0079,-0.00153,0.01646,-0.00886,0.03037,-0.01132,
-0.02321,-0.00137,0.02434,-0.0439,-0.03481,-0.03726,0.01744,
0.00075,0.02649,-0.01542,0.00592,0.03231,0.00873,-0.02915,
-0.01667,0.01128,-0.01562,-0.01816,0.0163,-0.00126,0.01141,
0.02476,-0.0104,-0.00947,0.00336,-0.01229,-0.00948,-0.02015,
0.021,0.0345,0.00417,0.0011,0.12514,-0.00488,-0.03353,0.0002,
0.00918,-0.01583,0.00166,0.00921,-0.00875,-0.01376,0.0079,
-0.00764,-0.00671,-0.00676,0.00524,0.0024,-0.00415,-0.01288,
0.01691,0.00006,0.01504,-0.00154,0.00155,-0.03329,0.00106,
-0.01481,0.01987,0.00421,0.02622,0.03251,0.00579,0.01364,
-0.00196,0.02125,0.01063,-0.0566,0.01431,0.0027,0.02983,
0.00724,0.00359,-0.00716,-0.00361,0.0181,0.01332,
0.00001,0.0007,-0.01034,0.01373,0.00044,-0.0934,
-0.01329,-0.04755,0.01595,0.01016,0.01325,
0.03563,0.00261,0.00521,-0.00173,0.02165,
-0.00429,-0.00931,-0.00086,-0.0086,0.01145,
-0.03361,0.02662,0.02506,-0.00506,-0.01017,
0.00685,0.00255,-0.00606,0.00524,-0.00849,
-0.00261,-0.01,0.01102,0.01295,0.00753,
0.00504,-0.01254,0.00762,0.00798,-0.00208,
-0.00041,0.0071,-0.0029,0.00208,0.00249,
0.01657,0.00244,-0.00397,0.0025,0.00163,
0.00081,-0.0065,-0.02858,-0.00115,0.00516,
0.00182,-0.02466,-0.04058,0.01324,0.00618,
-0.01316,0.00975,0.03436,-0.01311,0.00724,-0.01027,
-0.00865,0.01483,-0.01144,0.02114,-0.00937,
-0.00071,-0.01995,0.01229,-0.00867,-0.00962,
0.0159,0.01757,0.01094,-0.04649,-0.00975,-0.04131,
0.0062,0.00701,0.00825,0.01371,0.00316,0.01052,
-0.01351,0.00889,-0.00793,0.00168,-0.02776,-0.01018,
0.00561,-0.08457,0.03046,0.03448,0.00898,0.00999,
-0.00749,0.00094,0.02446,0.00826,-0.00688,-0.00729,
0.00691,-0.0046,0.01078,0.01346,-0.00536,-0.02488,
-0.01484,0.01318,-0.0053,-0.01886,0.0456,0.02459,
0.01005,0.02349,-0.02408,-0.01938,0.03819,-0.01236,
-0.04488,0.01283,-0.04437,-0.01422,-0.04424,0.01711,
-0.01088,0.043,0.04313,-0.01347,0.01087,-0.02281,
0.02051,0.03235,-0.01164,0.03173,0.02012,-0.00856,0.01215,-0.00696]二、题目分析
首先我们要知道什么是滑动窗口:
滑动窗口就相当于是双指针类型的题目。在left和right指针框起来的范围,就是需要进行相应判断的窗口。通过两个指针向前滑动,形成一个连续移动的矩形框窗口,对这个窗口内的元素进行相应判断。就是滑动窗口。
有了这个定义我们就很清楚啦 ,这题主要是分两步:
- 首先我们可以以窗口长度为3时举例,设定一个参数left为0,right为left+3,对股票序列进行截取,并且每截取一次left+=1,right+=1,这样就能不断截取;截取的列表求平均值,和索引为right的值取绝对值存到另一个列表fin_result中。直到right的值等于整个序列的长度,退出循环,对fin_result求和,并且除以计数器count即框选了多少次,就能求在窗口长度为3时的预测误差均值。
- 有了窗口长度为3举例,我们只要用for循环,从2到21中的每一个值作为窗格长度去求预测误差均值就好,思路都是一样的。最后用一个列表保存将值起来,并且用一个列表将窗口长度和对应的值关联起来,方便之后打印。
三、题目代码
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
"""
@Project :python
@File :python_23_4.py
@IDE :PyCharm
@Author :咋
@Date :2022/10/21 20:10
"""
#导入库
import matplotlib.pyplot as plt
import numpy as np
#设定画布。dpi越大图越清晰,绘图时间越久
num_list = [0.02931,0.048,0.0076,0.00302,
0.03759,-0.0058,-0.02738,0.00462,
0.00832,0.01201,-0.0095,0.01106,
-0.00728,0.02506,-0.00293,0.04029,
0,0.01134,0.00503,-0.00528,0.01363,
-0.00804,-0.02041,-0.00417,0.01918,
0.02333,-0.01979,0.00668,0.03198,0.04399,
-0.01258,-0.01274,-0.01649,-0.03191,0.0029,
0.03213,-0.02398,0.01543,0.0251,0.00361,0.03107,
-0.01619,-0.00253,0.00028,-0.00282,-0.00763,0.00128,
0.01592,0.05239,0.02994,-0.00001,-0.0231,-0.00014,
0.07143,0.00333,0,0.04983,-0.04114,0.0242,-0.02803,
0.03658,0.0079,-0.00153,0.01646,-0.00886,0.03037,-0.01132,
-0.02321,-0.00137,0.02434,-0.0439,-0.03481,-0.03726,0.01744,
0.00075,0.02649,-0.01542,0.00592,0.03231,0.00873,-0.02915,
-0.01667,0.01128,-0.01562,-0.01816,0.0163,-0.00126,0.01141,
0.02476,-0.0104,-0.00947,0.00336,-0.01229,-0.00948,-0.02015,
0.021,0.0345,0.00417,0.0011,0.12514,-0.00488,-0.03353,0.0002,
0.00918,-0.01583,0.00166,0.00921,-0.00875,-0.01376,0.0079,
-0.00764,-0.00671,-0.00676,0.00524,0.0024,-0.00415,-0.01288,
0.01691,0.00006,0.01504,-0.00154,0.00155,-0.03329,0.00106,
-0.01481,0.01987,0.00421,0.02622,0.03251,0.00579,0.01364,
-0.00196,0.02125,0.01063,-0.0566,0.01431,0.0027,0.02983,
0.00724,0.00359,-0.00716,-0.00361,0.0181,0.01332,
0.00001,0.0007,-0.01034,0.01373,0.00044,-0.0934,
-0.01329,-0.04755,0.01595,0.01016,0.01325,
0.03563,0.00261,0.00521,-0.00173,0.02165,
-0.00429,-0.00931,-0.00086,-0.0086,0.01145,
-0.03361,0.02662,0.02506,-0.00506,-0.01017,
0.00685,0.00255,-0.00606,0.00524,-0.00849,
-0.00261,-0.01,0.01102,0.01295,0.00753,
0.00504,-0.01254,0.00762,0.00798,-0.00208,
-0.00041,0.0071,-0.0029,0.00208,0.00249,
0.01657,0.00244,-0.00397,0.0025,0.00163,
0.00081,-0.0065,-0.02858,-0.00115,0.00516,
0.00182,-0.02466,-0.04058,0.01324,0.00618,
-0.01316,0.00975,0.03436,-0.01311,0.00724,-0.01027,
-0.00865,0.01483,-0.01144,0.02114,-0.00937,
-0.00071,-0.01995,0.01229,-0.00867,-0.00962,
0.0159,0.01757,0.01094,-0.04649,-0.00975,-0.04131,
0.0062,0.00701,0.00825,0.01371,0.00316,0.01052,
-0.01351,0.00889,-0.00793,0.00168,-0.02776,-0.01018,
0.00561,-0.08457,0.03046,0.03448,0.00898,0.00999,
-0.00749,0.00094,0.02446,0.00826,-0.00688,-0.00729,
0.00691,-0.0046,0.01078,0.01346,-0.00536,-0.02488,
-0.01484,0.01318,-0.0053,-0.01886,0.0456,0.02459,
0.01005,0.02349,-0.02408,-0.01938,0.03819,-0.01236,
-0.04488,0.01283,-0.04437,-0.01422,-0.04424,0.01711,
-0.01088,0.043,0.04313,-0.01347,0.01087,-0.02281,
0.02051,0.03235,-0.01164,0.03173,0.02012,-0.00856,0.01215,-0.00696]
all_result_dic = {}
all_result_list = []
y_list = []
for i in range(2,21):
fin_result = []
left = 0
count = 0
right = left+i
while True:
if right != len(num_list):
temp_1 = sum(num_list[left:right])/i
temp_2 = abs(num_list[right]-temp_1)
fin_result.append(temp_2)
left += 1
right += 1
count += 1
else:
break
all_result_dic[i] = sum(fin_result)/count
all_result_list.append(sum(fin_result)/count)
k2 = [k for k, v in all_result_dic.items() if v ==min(all_result_list)]
for i in range(2,21):
y_list.append(all_result_dic[i])
print("当移动窗口长度为:",i,"对应的误差为:",all_result_dic[i])
print("在[2:20]范围内使得该误差最小的移动窗格长度为:",k2[0],"对应的误差为:",all_result_dic[k2[0]])
fig=plt.figure(figsize=(4, 4), dpi=300)
#导入数据
x=list(np.arange(2, 21))
y= y_list
#绘图命令
plt.plot(x, y, lw=4, ls='-', c='b', alpha=0.1)
plt.plot()
#show出图形
plt.show()
#保存图片
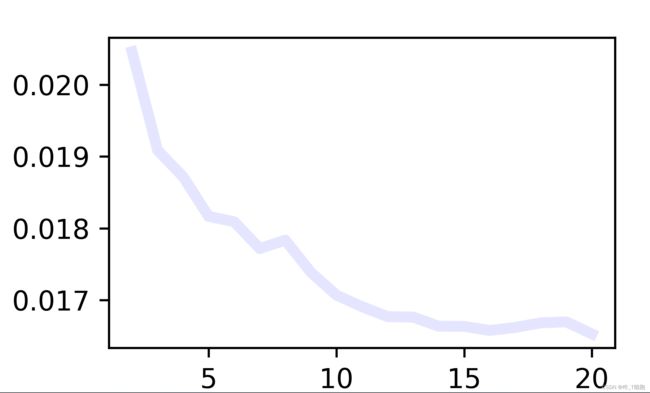
fig.savefig("画布")在最后,我用matplotlib.pyplot做了简单的可视化处理,使结果更加直观,运行结果为:
当移动窗口长度为: 2 对应的误差为: 0.020459651567944236
当移动窗口长度为: 3 对应的误差为: 0.01908844988344989
当移动窗口长度为: 4 对应的误差为: 0.018718245614035088
当移动窗口长度为: 5 对应的误差为: 0.018167260563380288
当移动窗口长度为: 6 对应的误差为: 0.01809260895170789
当移动窗口长度为: 7 对应的误差为: 0.01771991894630194
当移动窗口长度为: 8 对应的误差为: 0.017835907473309605
当移动窗口长度为: 9 对应的误差为: 0.017389440476190475
当移动窗口长度为: 10 对应的误差为: 0.017071688172043017
当移动窗口长度为: 11 对应的误差为: 0.0169103008502289
当移动窗口长度为: 12 对应的误差为: 0.01677201564380265
当移动窗口长度为: 13 对应的误差为: 0.016765702341137122
当移动窗口长度为: 14 对应的误差为: 0.016638602597402602
当移动窗口长度为: 15 对应的误差为: 0.016635518248175184
当移动窗口长度为: 16 对应的误差为: 0.016579548992673998
当移动窗口长度为: 17 对应的误差为: 0.01662127162629757
当移动窗口长度为: 18 对应的误差为: 0.01668552685526856
当移动窗口长度为: 19 对应的误差为: 0.0166987680311891
当移动窗口长度为: 20 对应的误差为: 0.016531403345724907
在[2:20]范围内使得该误差最小的移动窗格长度为: 20 对应的误差为: 0.016531403345724907四、总结
这道题目的难点在于left和right双变量的运用以及临界点的判断,需要熟悉掌握字典与列表的各项操作,如列表的添加,查找,字典根据值查找键。在最后,用数据可视化作图,使结果更加直观!
好啦,今天的分享就到这里啦,感兴趣的小伙伴欢迎评论区交流!