遗传算法详解python代码实现以及实例分析

遗传算法

---

---

前言

因为老师布置作业，需要我们用遗传算法来求函数的最大值，因此，在网上了解了一下遗传算法，并且找到几个实例，感觉求函数最大值还是蛮简单的，重要的是把这个过程走通，目前这里是用python写的，之后会补上一篇用C语言来写的（因为作业要求用C

---

一、遗传算法是什么？

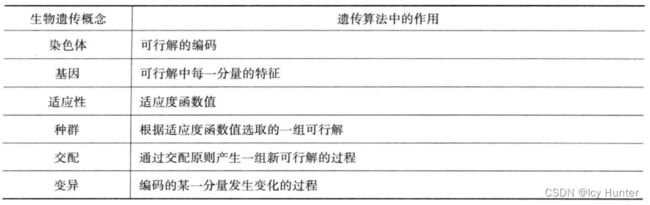
简单来说，就是通过模拟生物生殖、变异，根据适者生存的原则，挑选出最后留下的生物，作为问题的最优解。一般遗传算法用于优化问题，用于解决一些求精确解是否困难的问题，例如旅行商问题，复杂函数的极值问题等等。

二、实例讲解

例题1

这个是在b站上看到的一个例子，其实是十分的简洁的。
给出链接：https://www.bilibili.com/video/BV1Yg411T7W2?spm_id_from=333.1007.top_right_bar_window_history.content.click
问题描述：在一个长度为n的数组nums中选择10个元素，使得10个元素的和与原数组的所有元素之和的1/10无限接近。
如n=50, sum(nums)=1000, 选择元素列表answer要满足|sum(answer)-1000|

1.初始化种群

生成50个范围从0到1000的随机数。

import random
def create_answer(number_set, n):  # 随机选择n个数作为答案，据题意选择n=10
    result = []
    for i in range(n):
        result.append(random.sample(number_set, 10))
    return result

number_set = random.sample(range(0, 1000), 50)
middle_answer = create_answer(number_set, 100)  # 随机选择100个答案（种群）

2.优胜劣汰

计算每个答案与正确答案的偏离程度，计算适应度（错误率

def error_level(new_answer, number_set):  # 计算错误率，错误率越小遗传的概率越大
    error = []
    right_answer = sum(number_set) / 10
    for item in new_answer:
        value = abs(right_answer - sum(item))
        if value == 0:
            error.append(10)
        else:
            error.append(1 / value)
    return error

3.根据优胜劣汰的结果，交配生殖、变异

def variation(old_answer, number_set, pro):  # 0.1的变异概率
    for i in range(len(old_answer)):
        rand = random.uniform(0, 1)
        if rand < pro:
            rand_num = random.randint(0, 9)
            old_answer[i] = old_answer[i][:rand_num] + random.sample(number_set, 1) + old_answer[i][rand_num+1:]
    return old_answer

def choice_selected(old_answer, number_set):  # 交叉互换模拟交配生殖的结果
    result = []
    error = error_level(old_answer, number_set)
    error_one = [item / sum(error) for item in error]
    for i in range(1, len(error_one)):
        error_one[i] += error_one[i - 1]
    for i in range(len(old_answer) // 2):
        temp = []
        for j in range(2):
            rand = random.uniform(0, 1)
            for k in range(len(error_one)):
                if k == 0:
                    if rand < error_one[k]:
                        temp.append(old_answer[k])
                else:
                    if rand >= error_one[k-1] and rand < error_one[k]:
                        temp.append(old_answer[k])
        rand = random.randint(0, 6)
        temp_1 = temp[0][:rand] + temp[1][rand:rand+3] + temp[0][rand+3:]
        temp_2 = temp[1][:rand] + temp[0][rand:rand+3] + temp[1][rand+3:]
        result.append(temp_1)
        result.append(temp_2)
    return result

5.生物遗传进化

number_set = random.sample(range(0, 1000), 50)
middle_answer = create_answer(number_set, 100)
first_answer = middle_answer[0]
greater_answer = []
for i in range(1000): #
    error = error_level(middle_answer, number_set)  # 计算适应度
    index = error.index(max(error))
    middle_answer = choice_selected(middle_answer, number_set)
    middle_answer = variation(middle_answer, number_set, 0.1)
    greater_answer.append([middle_answer[index], error[index]])

greater_answer.sort(key=lambda x: x[1], reverse=True)
print("正确答案为", sum(number_set) / 10)
print("给出最优解为", greater_answer[0][0])
print("该和为", sum(greater_answer[0][0]))
print("选择系数为", greater_answer[0][1])
print("最初解的和为", sum(first_answer))

for i in greater_answer[0][0]:
    if i in number_set:
        print(i)

运行结果（不定：

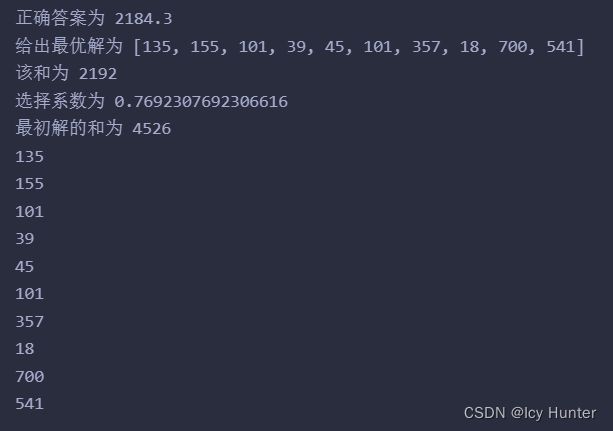
这个是我开始学习遗传算法最开始学的一个例题，其实现在回过头来看，这个代码其实写的通用性并不强，并且核心思想并不突出，例如DNA的概念并不强，可能是题目类型不同，和求复杂函数极值问题的代码还是有些差别的，但是遗传算法的思想本质是有的，因此拿来讲讲。

例题2

遗传算法详解 附python代码实现
这就是一个是用遗传算法求函数极值的例子，里面有可视化，有代码，还是挺不错的，用上了numpy矩阵运算，效率十分不错，不过我感觉对于初学者来说可能有点难理解，而且我感觉里面对于DNA编码解码的那块有点问题，实际上直接使用二进制转换为十进制就可以了。因此，我参考这篇博客，自己重新写了一遍代码。下面将讲解我的代码思路。

1.初始化参数

我是将DNA组合为animal模拟一个生物，然后每个DNA用二进制编码，DNA_bit是表示一个DNA的大小由符号位（1位）+数据位组成，数据位由整数位和小数位组成。
DNA数据位中Int_bit则表示整数的位数，例如Int_bit=2则表示整数部分为00-11,转换为十进制就是0-3。
DNA_num则表示一个animal有多少个DNA，每条DNA都是DNA_bit大小，可以理解为能够表示几个数，这里有两个数x,y，因此两个DNA就足够了。
剩下参数应该好理解。

import numpy as np
import math

DNA_bit = 13 # 一个DNA的二进制位数,(第一维表示符号位)
Int_bit = 2  # DNA_bit-1（符号位bit）之后整数占的bit位
DNA_num = 2  # DNA的个数
animal_num = 200 # 开始种群的数量 
cross_rate = 0.8 # 生殖交叉概率
variation_rate = 0.005  # 变异的概率
generator_n = 50 # 种群演变的次数
limit_area = [-3, 3] # 值域

2.定义环境（定义目标函数）

这题就是求这个复杂函数的最大值，模拟生物生存的环境

def f(x, y):
    return 3*(1-x)**2*np.exp(-(x**2)-(y+1)**2)- 10*(x/5 - x**3 - y**5)*np.exp(-x**2-y**2)- 1/3**np.exp(-(x+1)**2 - y**2)

3.DNA解码（计算x，y）

这个函数每次传入的是一个animal即两个DNA的组合，解码出来的结果就是所表示的x，y

def translate_DNA(animal):  # 解码种群的DNA
    def DNA2t10(DNA):
        sum = 0
        sign = DNA[0]
        data = DNA[1:]
        if sign == 0:  # 符号位赋值
            flag = -1
        else:
            flag = 1
        
        for i in range(0, Int_bit):
            if data[i] == 1:
                sum += math.pow(2, Int_bit - i - 1)
        for i in range(Int_bit, len(data)):
            if data[i] == 1:
                sum += math.pow(2, Int_bit - i - 1)
        return flag * sum
    DNA_result = []
    for i in range(0, DNA_bit * DNA_num, DNA_bit):
        DNA = animal[i:i+DNA_bit]
        translated_DNA = DNA2t10(DNA)
        DNA_result.append(translated_DNA)
    return DNA_result

4.初始化种群（初始化解，考虑定义域）

由于可能由定义域的限制，因此在初始化种群的时候，确保所有的种群都符合定义域（大环境）

def flag_limit_area(animal, limit_area):  # 判断种群是否符合值域，否则一票否决
    x, y = translate_DNA(animal)
    if x <= limit_area[1] and x >= limit_area[0] and y <= limit_area[1] and y >= limit_area[0]:
        return True
    else:
        return False
        
# 初始化种群，需要判断开始的种群是否符合值域
animals = np.random.randint(2, size=(animal_num, DNA_bit * DNA_num))
# 每个animal由两个DNA组成，每个DNA为DNA_bit位

num = animal_num
while(num):
    pos = num - 1
    if flag_limit_area(animals[pos], limit_area):
        num -= 1
    else:
        animals[pos] = np.random.randint(2, size=(1, DNA_bit * DNA_num))

5.计算适应度（计算误差，考虑定义域）

根据目标函数，计算出误差，由于这里是要求最大值，因此带入函数结果越大，适应度也就越大。这里需要考虑是否符合定义域的情况，不符合一票否决。

def get_fitness(animals):  # 计算种群各个部分的适应度
    fitness_score = np.zeros(len(animals))
    fit_flag = np.zeros(len(animals))
    for i in range(len(animals)):
        x, y = translate_DNA(animals[i])
        fitness_score[i] = f(x, y)
        if flag_limit_area(animals[i], limit_area):
            fit_flag[i] = 1
        else:
            fit_flag[i] = 0
    fitness_score = (fitness_score - np.min(fitness_score)) + 1e-5
    fitness_score = fitness_score * fit_flag # 如果不符合定义域就不取了
    fitness_p = fitness_score / (fitness_score.sum())  # 计算被选择的概率
    return fitness_p 

6.适者生存（挑选误差较小的答案）

根据之前的适应度的结果，误差越小适应度大，可以转换为概率，因此被留下的概率也就越大。

def select_animal(animals, fitness):  # 按照适应度选择留下的种群
    idx = np.random.choice(np.arange(animal_num), size=animal_num, replace=True, p=(fitness)/(fitness.sum() + 1e-8))
    return animals[idx]

7.生殖、变异（更改部分二进制位，取反部分二进制位，可能生成误差更小的答案）

def variation(children, variation_rate):  # 模拟编译
    if np.random.rand() < variation_rate: #以MUTATION_RATE的概率进行变异
        mutate_point = np.random.randint(0, DNA_bit * 2)  # 随机产生一个实数，代表要变异基因的位置
        children[mutate_point] = children[mutate_point] ^ 1  #这一位取反
    return children
 

def crossover_and_variation(animals, cross_rate):  # 模拟生殖过程（包括交配和变异）
    new_animals = []
    for father in animals:
        child = father		# 选择父亲
        if np.random.rand() < cross_rate:	#产生子代时不是必然发生交叉，而是以一定的概率发生交叉
            mother = animals[np.random.randint(animal_num)]	#再选择母亲
            cross_points = np.random.randint(low = 0, high = DNA_bit * DNA_num)	#随机产生交叉的点
            child[cross_points:] = mother[cross_points:] # 交叉互换，模拟生殖
        variation(child, variation_rate)	#变异
        new_animals.append(child)
    return np.array(new_animals)

8.查看最终的答案

def get_result(animals):  # 获取结果
    fitness = get_fitness(animals)
    max_fitness_index = np.argmax(fitness)
    print("max_fitness:", fitness[max_fitness_index])
    x, y = translate_DNA(animals[max_fitness_index])
    print("最优的基因型：", animals[max_fitness_index])
    print("(x, y):", (x, y), f(x, y))
    return

9.生物遗传进化

# 模拟进化选择generator_n轮    
for i in range(generator_n):
    fitness_score = get_fitness(animals)  # 计算适应度
    selected_animals = select_animal(animals, fitness_score) # 适者生存
    animals = crossover_and_variation(selected_animals, cross_rate)  # 生殖、变异

10.完整代码

import numpy as np
import math

DNA_bit = 13 # 一个DNA的二进制位数,(第一维表示符号位)
Int_bit = 2  # DNA_bit-1（符号位bit）之后整数占的bit位
DNA_num = 2  # DNA的个数
animal_num = 200 # 开始种群的数量 
cross_rate = 0.8 # 生殖交叉概率
variation_rate = 0.005  # 变异的概率
generator_n = 50 # 种群演变的次数
limit_area = [-3, 3]

def f(x, y):
    return 3*(1-x)**2*np.exp(-(x**2)-(y+1)**2)- 10*(x/5 - x**3 - y**5)*np.exp(-x**2-y**2)- 1/3**np.exp(-(x+1)**2 - y**2)

def translate_DNA(animal):  # 解码种群的DNA
    def DNA2t10(DNA):
        sum = 0
        sign = DNA[0]
        data = DNA[1:]
        if sign == 0:  # 符号位赋值
            flag = -1
        else:
            flag = 1
        
        for i in range(0, Int_bit):
            if data[i] == 1:
                sum += math.pow(2, Int_bit - i - 1)
        for i in range(Int_bit, len(data)):
            if data[i] == 1:
                sum += math.pow(2, Int_bit - i - 1)
        return flag * sum
    DNA_result = []
    for i in range(0, DNA_bit * DNA_num, DNA_bit):
        DNA = animal[i:i+DNA_bit]
        translated_DNA = DNA2t10(DNA)
        DNA_result.append(translated_DNA)
    return DNA_result

def flag_limit_area(animal, limit_area):  # 判断种群是否符合值域，否则一票否决
    x, y = translate_DNA(animal)
    if x <= limit_area[1] and x >= limit_area[0] and y <= limit_area[1] and y >= limit_area[0]:
        return True
    else:
        return False

def get_fitness(animals):  # 计算种群各个部分的适应度
    fitness_score = np.zeros(len(animals))
    fit_flag = np.zeros(len(animals))
    for i in range(len(animals)):
        x, y = translate_DNA(animals[i])
        fitness_score[i] = f(x, y)
        if flag_limit_area(animals[i], limit_area):
            fit_flag[i] = 1
        else:
            fit_flag[i] = 0
    fitness_score = (fitness_score - np.min(fitness_score)) + 1e-5
    fitness_score = fitness_score * fit_flag # 如果不符合定义域就不取了
    fitness_p = fitness_score / (fitness_score.sum())  # 计算被选择的概率
    return fitness_p 


def select_animal(animals, fitness):  # 按照适应度选择留下的种群
    idx = np.random.choice(np.arange(animal_num), size=animal_num, replace=True, p=(fitness)/(fitness.sum() + 1e-8))
    return animals[idx]


def variation(children, variation_rate):  # 模拟编译
    if np.random.rand() < variation_rate: #以MUTATION_RATE的概率进行变异
        mutate_point = np.random.randint(0, DNA_bit * 2)  # 随机产生一个实数，代表要变异基因的位置
        children[mutate_point] = children[mutate_point] ^ 1  #这一位取反
    return children
 

def crossover_and_variation(animals, cross_rate):  # 模拟生殖过程（包括交配和变异）
    new_animals = []
    for father in animals:
        child = father		# 选择父亲
        if np.random.rand() < cross_rate:	#产生子代时不是必然发生交叉，而是以一定的概率发生交叉
            mother = animals[np.random.randint(animal_num)]	#再选择母亲
            cross_points = np.random.randint(low = 0, high = DNA_bit * DNA_num)	#随机产生交叉的点
            child[cross_points:] = mother[cross_points:] # 交叉互换，模拟生殖
        variation(child, variation_rate)	#变异
        new_animals.append(child)
    return np.array(new_animals)
    
def get_result(animals):  # 获取结果
    fitness = get_fitness(animals)
    max_fitness_index = np.argmax(fitness)
    print("max_fitness:", fitness[max_fitness_index])
    x, y = translate_DNA(animals[max_fitness_index])
    print("最优的基因型：", animals[max_fitness_index])
    print("(x, y):", (x, y), f(x, y))
    return

# 初始化种群，需要判断开始的种群是否符合值域
animals = np.random.randint(2, size=(animal_num, DNA_bit * DNA_num))
num = animal_num
while(num):
    pos = num - 1
    if flag_limit_area(animals[pos], limit_area):
        num -= 1
    else:
        animals[pos] = np.random.randint(2, size=(1, DNA_bit * DNA_num))

# 模拟进化选择generator_n轮    
for i in range(generator_n):
    fitness_score = get_fitness(animals)
    selected_animals = select_animal(animals, fitness_score)
    animals = crossover_and_variation(selected_animals, cross_rate)

get_result(animals)

运行结果（不定：

这里因为是我自己写的，亲儿子，所有我会觉得比较好理解，就是没有使用矩阵乘法，可能速度会有点问题，但是，初学者理解起来应该会比较简单，没事，哪里有问题改哪里就好了。

总结

遗传算法的大概思路就是模拟生物的优胜劣汰、适者生存，还是很生动形象，因为是比较简单的例子，可能代码还是会有很多地方考虑步骤，但是对我的作业来说还是足够了。
作业如下：


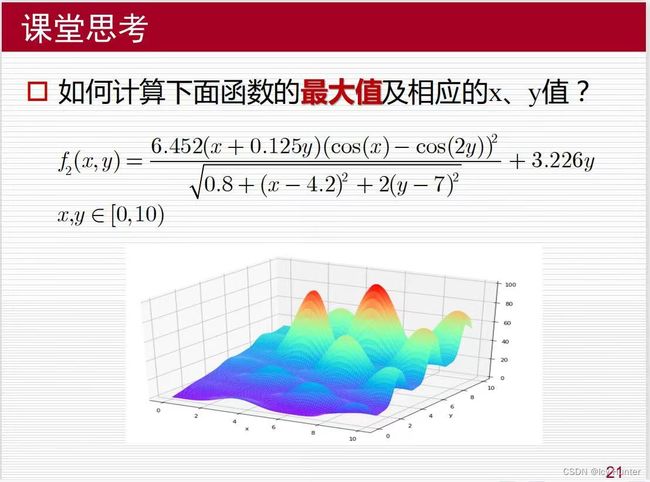
代码我就不贴了，上面随便改改就好了，这是我的运行结果，你们可以试试。