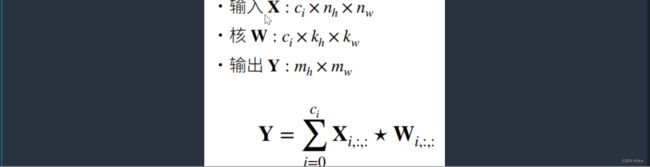【动手学深度学习PyTorch版】14 卷积层里的多输入多输出通道

目录

一、卷积层里的多输入多输出通道

1.1 多输入多输出通道

◼ 多个输入通道

◼ 多输出通道

◼ 1*1卷积核

◼ 二维卷积层

◼ 总结

二、代码实现

2.1 输入与输出（使用自定义）

◼ 多输入多输出通道互相关运算

2.2 1X1卷积（使用自定义）

2.3 1X1卷积（使用框架）

---

一、卷积层里的多输入多输出通道

1.1 多输入多输出通道

◼ 多个输入通道

通常来说，我们会用到彩色图片，彩色图像一般是由RGB三个通道组成的。彩色图片一般会有更加丰富的信息。

但是转换为灰度会丢失信息，所以在图片的表示中通道数应该是3。我们之前都是只用了一个通道，简单图片对于单通道来说还是ok的，但是对于复杂图像就不行了。

假设图片的大小为200x200，那么图像的张量表示应该是200x200x3，不仅仅是一个简单的矩阵了。

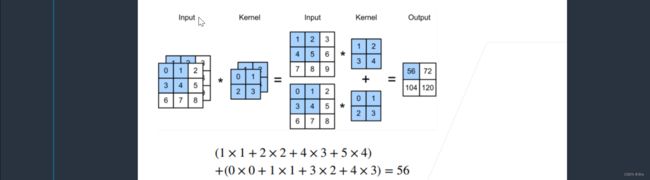
当输入有了多个通道之后，假设有2个通道，Input中，前面的是通道0，后面是通道1。那么每个通道就会需要一个卷积核，比如针对通道0的卷积核对通道0做卷积，针对通道1的卷积核对通道1做卷积。再按元素相加，得到我们最终的结果。

① 核的通道数与输入的通道数一样。如果有多个通道，每一个通道都有一个卷积核，结果是所有通道卷积结果的和。

我们假设：

卷积核也会对应的变成三维的矩阵，但是输出是一个单通道，因为不管输入是多少通道，输出是把结果相加之后产生的。也就是说对每一个通道，把它对应的输入和对应的核做卷积，再按元素相加起来，得到输出。

◼ 多输出通道

无论有多少通道的输入，到目前为止不论有多少输入通道，我们只会得到单输出通道。

如果我们希望输出是多维的，得到多输出通道该怎么办呢？

做法是对每一个输出都有一个自己的三维的卷积核，总共设置多个三维的卷积核，每一个卷积核计算出来的结果作为一个通道，把每一个通道一一做运算，再把它们concat起来得到我们的输出。

相比于之前单输出通道多了一个参数Co。输出通道数，即卷积核的个数是卷积层的另一个超参数。

输出里面的第i个通道，其实就是完整的输入X与对应第i个核，做多输入的卷积，然后对所有的i做遍历。

这样就得到了多输出通道的结果。

那为什么要这么做呢？

我们可以认为每一个通道识别出来的都是一些特殊的模式，这是输出通道干的事情。

多输入通道干什么呢？假设我把这6个通道丢给下一层，下一层要把这每个模式识别出来并组合起来，得到一个组合的模式序列。

当然， 每一层有多个输出通道时至关重要的。

在最流行的神经网络架构中，随着神经网络层数的加深，我们常会增加输出通道的维数，通过减少空间分别率以获得更大的通道深度。

比如说，我们可以先识别猫的胡须，耳朵，再往上走的话，把这些纹理组合起来，在上层的一些卷积层可能就是识别的猫头。

直观地说，我们可以将每个通道看作是对不同特征的响应。而现实可能更为复杂一些，因为每个通道不是独立学习的，而是为了共同使用而优化的。

因此，多输出通道并不仅是学习多个单通道的检测器。

◼ 1*1卷积核

(1,1)的卷积核是一个常用的卷积核，它并不能识别空间信息，它的作用是融合通道。

因为1x1卷积层每次只识别一个像素，而不查看该像素与周围像素的关系，所以它并不识别空间信息。

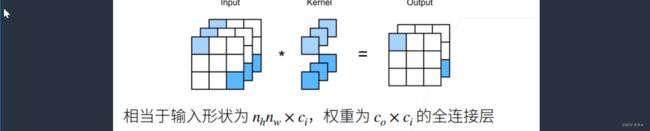
等价于把整个NhxNw的输入拉成一个长为NhNw的向量，也就是说空间信息没有了，然后通道数拉成特征数Ci。将卷积核重新写成CoxCi，等价于输入为NhxNwxCi，权重为CoxCi的全连接层。

◼ 二维卷积层

 模型存储挺小的，但是计算量不一定小。

◼ 总结

二、代码实现

2.1 输入与输出（使用自定义）

◼ 多输入多输出通道互相关运算

（1）实现一下多输入通道互相关运算：

假设X和K是3D的，将X和K zip起来，每次zip就会对输入通道的维数进行遍历，即每次for拿出对应的输入通道里的那个小矩阵，然后把它做互运算，对所有通道求和。

import torch 
from d2l import torch as d2l

def corr2d_multi_in(X, K):
    return sum(d2l.corr2d(x, k) for x,k in zip(X,K))

（2）验证互相关运算的输出：

# 这是多通道输入（2，3，3），单通道输出（2，2），两个核（2，2）
# 一个核对应一个通道
X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
               [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])

corr2d_multi_in(X, K)

（3）计算多个通道的输出的互相关函数：

假设X是3D的，K是4D的，最外层是输出通道数。

对每一个输出通道的K拿出它对应的3D核K。

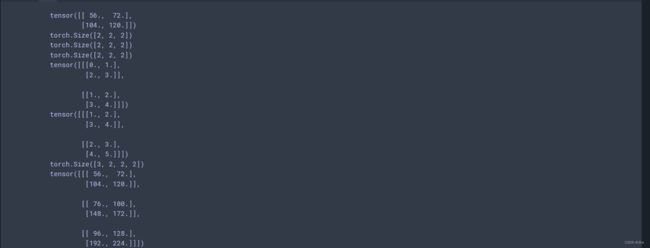
现在一个核有多个通道，每一个核的形状是（2, 2, 2），共有三个核（3，2，2，2）。

一个卷积核经过一次操作后会得到单通道的输出（2，2），下面这个操作就是让每一个卷积核得到的一个通道的输出，堆叠起来----------（3，2，2）。

# 计算多个通道的输入输出
def corr2d_multi_in_out(X,K):
    # 现在一个核有多个通道，每一个核的形状是（2, 2, 2），共有三个核（3，2，2，2）
    # 一个卷积核经过一次操作后会得到单通道的输出（2，2）
    # 下面这个操作就是让每一个卷积核得到的一个通道的输出，堆叠起来。（3，2，2）
    return torch.stack([corr2d_multi_in(X,k) for k in K])

# 创建三个卷积核
K = torch.stack((K, K + 1, K + 2), 0)
print(type(K))
# print(K.shape)

corr2d_multi_in_out(X,K)

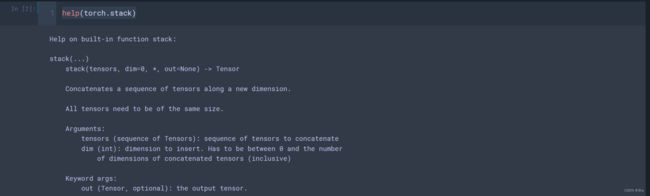
help(torch.stack)

2.2 1X1卷积（使用自定义）

验证1X1卷积等价于一个全连接？

• 创建3x3的数入X；
• K：输出通道为2，输入通道为3，核为1x1；

# 1*1的卷积核
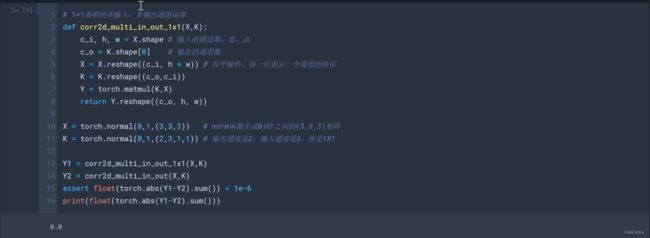
def corr2d_multi_in_out_1x1(X, K):
    c_i,h,w = X.shape
    c_o = K.shape[0]    # K的第一个shape
    # 这里就是将一张图片的高和宽展平成一条直线(3, 3, 3) => (3,9)
    # 剩下（channel_num，input）
    X = X.reshape((c_i,h*w))    # c_i是通道数
    # 把卷积核的高和宽展平成一条直线(2, 3, 1, 1) => (2,3)，剩下（kernel_num, kernnel），就变成了一个矩阵
    K = K.reshape((c_o,c_i))    # 这样，X和K都是一个矩阵了
    Y = torch.matmul(K,X)    # 那么直接调用矩阵乘法，将K*X
    print(X.shape,K.shape,Y.shape)
    return Y.reshape((c_o, h, w))    # 最后的Y

X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))    # 输出通道为2，输入通道为3，核为1x1

Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6  # 如果小于1e-6，可以认为几乎完全一样 

2.3 1X1卷积（使用框架）

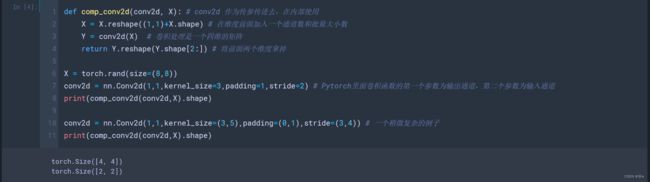
def comp_conv2d(conv2d, X): # conv2d 作为传参传进去，在内部使用
    X = X.reshape((1,1)+X.shape) # 在维度前面加入一个通道数和批量大小数
    Y = conv2d(X)  # 卷积处理是一个四维的矩阵
    return Y.reshape(Y.shape[2:]) # 将前面两个维度拿掉

X = torch.rand(size=(8,8))
conv2d = nn.Conv2d(1,1,kernel_size=3,padding=1,stride=2) # Pytorch里面卷积函数的第一个参数为输出通道，第二个参数为输入通道   
print(comp_conv2d(conv2d,X).shape) 

conv2d = nn.Conv2d(1,1,kernel_size=(3,5),padding=(0,1),stride=(3,4)) # 一个稍微复杂的例子
print(comp_conv2d(conv2d,X).shape)

输入的高宽都减半的情况下，通常会把输出的通道数加一倍。（空间信息压缩了，把提取出来的信息保存在更多的通道里）。