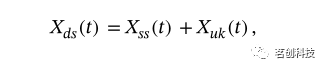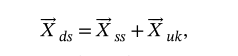心算任务诱发fNIRS波动的频域分析

大家好，这里是 “茗创科技” 。茗创科技专注于脑科学数据处理，涵盖（EEG/ERP, fMRI,结构像,DTI,ASL, ,FNIRS）等，欢迎留言讨论及转发推荐，也欢迎了解茗创科技的脑电课程，数据处理服务及脑科学工作站销售业务，可添加我们的工程师（MCKJ-zhouyi或17373158786）咨询。

导读

功能性近红外光谱（fNIRS）是一种越来越多地用于认知过程的神经成像技术。然而，fNIRS信号通常会受到非脑源的任务诱发和自发血流动力学振荡的影响，这也是fNIRS研究面临的一个挑战。为了分离任务诱发的皮层反应，研究者考察了脑力活动中浅层和深层血流动力学变化之间的耦合。为此，本研究应用了一个有节奏的心算任务，来诱发适用于有效频率分辨测量的周期性血流动力学波动。20名年龄在18-25岁之间的大学生（8名男性）参与了这项任务，同时使用新开发的NIRS设备监测前额的血流动力学变化，该设备能够进行多通道和多距离记录。研究结果发现氧合血红蛋白和脱氧血红蛋白存在显著的任务相关波动，在浅层和深层组织之间高度一致，证实了表层血液动力学对深层fNIRS信号的强烈影响。重要的是，通过线性回归去除这些表面噪声后，发现额叶皮层对心算任务的反应遵循一种不同寻常的逆氧合模式。此研究首次应用基于传递函数分析和相量代数的替代方法来估计神经信号，从而证实了这一发现。总而言之，本研究结果证明了使用有节奏的心理任务来施加振荡状态的可行性，这种振荡状态有助于区分真实的大脑功能反应和非脑源的反应。

1.引言

fNIRS研究中的一个主要挑战是有效地将神经血管耦合引起的血流动力学反应与其他混杂成分分开。由大脑活动引起的fNIRS变化幅度自然较低，而且还与其他噪声波动重叠，主要是：（i）在大脑和脑外区域均可检测到全身血流动力学活动，（ii）头表组织层的局部血流变化，以及（iii）仪器噪声和其他伪影。前两种情况不仅可以自发地产生，还可以通过认知、情绪或身体任务诱发。如果这些非皮层任务相关的信号成分的改变模拟了感兴趣的大脑激活动态，那么它们可能成为干扰和噪声的重要来源。前人研究表明，与任务相关的皮肤血流变化可以解释语言流畅性实验中90%以上的NIRS信号，并且进一步证明了动脉血压波动会造成的强烈噪声。

为了更好地推断功能性响应的存在，实验方案试图通过重复足够次数的刺激来增加统计效力，其间穿插着预期会出现不同反应（或无反应）的对比条件。为此，fNIRS实验通常使用block或事件相关设计，这取决于研究者们是否想分别分析持续或瞬态响应。事件设计使用短时刺激，通常按随机顺序呈现，并以恒定或变化的刺激间隔开来。Block设计通过呈现一个有足够长时间间隔的刺激条件，然后是一个不同的条件或休息的刺激间隔来维持心理参与。为了研究“持续”和“瞬时”响应之间的相互作用，也可以使用混合设计。

根据刺激呈现策略，已经开发了不同的分析方法来推断功能性血流动力学反应，并将其与噪声分开。虽然经典的平均策略提供了稳健的结果，但通常基于平均的统计检验，如t检验或ANOVA，不允许估计fNIRS信号的形状或时间过程，因此它们已逐渐被其他方法所取代。其中包括一般线性模型（GLM）框架、数据驱动方法（如主成分分析和独立成分分析）和动态状态空间模型（DSSM）。GLM是最广泛采用的统计框架之一，用于量化测量的fNIRS信号与反映预期神经反应的血流动力学模型的匹配程度。它利用了fNIRS良好的时间分辨率，并允许在回归模型中包含不同的协变量（例如生理信号）。在最基本的形式中，该模型是通过将血流动力学响应函数（HRF）与刺激函数进行卷积获得的，该刺激函数对神经元响应的假设时间过程进行编码。因此，GLM是一种假设驱动的方法，需要结合特定的HRF（通常取自fMRI研究）和其他回归因子来构建线性模型，根据任务类型、大脑区域和被试的特质，线性模型可能不明显。此外，由于一些统计问题，GLM在应用于fNIRS信号时需要特别小心。相比之下，“主成分”和“独立成分”分析方法分别依赖于正交性和独立性等一般统计假设。虽然对于分离组成fNIRS信号的混合成分很有用，但它们需要额外的处理来阐明其中哪些与任务相关，哪些与任务无关，尤其是当脑外和脑内反应相关时。主要基于卡尔曼滤波的SSM允许建立复杂的血流动力学模型来描述fNIRS信号的时变特征，并估计HRF。虽然动态分析似乎能更好地估计HRF，并更好地解释非平稳信号，但它仍需要改进模型规格和状态空间估计器。

无论每种实验方法的优缺点如何，所有这些方法都得益于包含短距离记录，以获得表层对fNIRS信号影响的参考。多距离测量被认为能有效分离实际的大脑响应。然而，仍有一些待解决的问题，如，源探测器距离的理想范围、短距通道的最佳数目以及它们相对于长距通道的布置。理想的情况是，每个长通道应该至少与一个附近的短通道配对。但目前最常用的NIRS设备无法实现这种配对测量的精确空间配置。

研究者的兴趣集中在研究大脑活动过程中，由表层和深层引起的血流动力学变化之间的耦合，并从噪声中分离出任务诱发的皮层反应。背后的基本原理是：假设脑外和大脑的反应是不同但相互关联过程的协调效应下的结果。将表面波动看作是有价值信息的载体，而不只是必须去除的噪声。信息不仅可以更好地理解fNIRS数据，也可以更准确地评估完整的神经-内脏动态联系。但自发波动和任务锁定波动的难以区分阻碍了这一目标的实现。一种可能的解决办法是人为引起周期性振荡，这样就可以很容易地使用频域方法进行定位和分析。

本研究假设执行循环认知任务也会引起fNIRS可测量的周期性血液动力学波动。为了验证这一假设，本研究设计了一种适用于在频域进行有效分析的振荡状态。采用特定频率循环block设计的心算任务，同时使用新开发的多通道NIRS设备对前额进行密集的多距离记录。同时持续监测心率记录心脏活动。

分析频域信号之间的幅度和相位关系将允许:(i)识别常见的与任务相关的振荡活动，(ii)估计浅层和深层组织层对fNIRS信号的贡献，(iii)将任务相关的表面血流动力学与假定的皮层反应分离，(iv)测量HbO和HbR变化的相对时间，以更好地解释潜在的生理过程。此外，使用经验传递函数作为一种替代方法来评估脑功能活动和评估脑外和大脑反应之间的时间协调。这种方法以前从未在fNIRS研究中进行过测试。

2.方法

所有数据处理均使用MATLAB（R2019a，Mathworks，Natick，MA，USA）离线完成，使用原生函数、自制脚本和开源包。

2.1被试：24名志愿者，事先练习任务10-15 min确保其理解任务要求。

2.2心理任务：采用思维活动循环模式，即心算阶段与相同持续时间的停顿阶段交替进行，即有规律地重复活动-休息。实验过程如图所示：

图1.实验过程示意图。

2.3心率测量

使用BIOPAC MP36生理监测系统和AcqKnowledge软件4.1记录ECG，采样率为500Hz；采用AcqKnowledge对原始数据进行后续的处理: (i)使用Pan-Tompkins算法，从ECG信号创建R-R血流速度图，用于R波检测；(2)从血流速度图的倒数中提取瞬时心率。最后，将数据导出到MATLAB中，利用三次样条插值将数据重采样至10Hz。

2.3.1心率排除标准

与基线时的平均心率相比，任务期间的阈值被设置为每分钟最多增加12次（bpm）。两名被试因超过该阈值而被排除在外，最终样本量N=22。因此，只有那些在基线和任务期间心率相当稳定的被试被进一步考虑。使用Wilcoxon符号秩次检验来解决基线和任务期间的最大心率之间的差异。

2.4 fNIRS记录

图2.探针几何形状和放置示意图。(a)光极排列(黄色方块：光源；白色圆圈：探测器)。16个短通道(带数字的黑线)和12个长通道(带字母的绿线)。(b)前额上的探头位置。绿色阴影区域大致标记了长通道所探测的区域。黑色矩形勾勒出每个ROI(右、中、左)内平均的长通道。

2.4.1信号质量检查：通道和被试的排除标准

评估原始光学数据，以识别出极值通道（低于5%或高于95%的范围），或变异系数大于7.5%（计算为标准差和均值之间的百分比）。排除信噪比差的数据，矫正了运动伪影，排除了两名被试，最终样本由20名被试组成。

2.4.2 fNIRS数据预处理

使用基于MATLAB的Homer2 NIRS工具包进行预处理。将原始光学数据转换为光密度，然后通过改进的Beer-Lambert定律转换为氧([HbO])和脱氧血红蛋白([HbR])相对浓度的变化。使用了一个微分路径长度因子，该因子考虑了被试的年龄和波长。未使用部分容积校正。

fNIRS 数据通过使用零相位、5阶巴特沃斯滤波器进行低通滤波，截止频率为2.5Hz；未采用高通滤波。去除高频噪声，同时保留心脏、呼吸、血压和血管运动的成分。预处理后，从每个发色团中分别得到16个短通道的时间序列和12个被称为“浅信号”和“深信号”的长通道的时间序列，以指示在相应的记录中穿透了多少光。因此，研究者有一组多距离记录，以有效地解决脑外污染问题，假设短间隔记录只对脑外变化敏感，而长间隔记录对脑外和大脑活动都敏感。

当使用多距离记录进行回归时，可以假设生理噪声在浅层和深层信号中的时间进程具有可比性，且由任务诱发的脑血流动力学是独立的。然而，不能忽略局部表面波动的异质性，这就需要在尽可能接近深层信号的记录位置收集浅层信号，以便从表面血液动力学中去除噪声。研究者使用了一个NIRS设备，它允许每个深层信号有三个满足接近要求的浅信号：两个分别靠近长通道的探测器和源，一个靠近其中心（见图2a）。采用“双短间隔测量”方法，使用在探测器和源附近记录的两个浅层信号的组合来估计对应的深层信号。因此，例如，来自长通道“A”的信号对来自短通道1和5的信号求和进行回归（图2）。在整个时间过程中，对于计算的所有深层信号公式如下：

其中β0和β1为回归系数，Sdeep为深信号，Sshallow由浅层信号和干净信号（Ssclean）组成（实际上是原始残差）。使用MATLAB函数“robustfit”来求解线性回归，该函数使用迭代重加权最小二乘算法，对异常值的敏感性低于普通最小二乘法。回归后，每个Sdeep都有其关联的一对Ssclean和Sshallow。这一预防措施是基于：心理任务试图诱发周期性振荡，可能无法满足脑外和脑血流动力学之间不相关的要求，从而影响了回归的表现。之后，在此研究中，将应用额外的分析来验证这些回归估计信号的性质。

最后，由于头部形状和大小的可变性，通道位置在个体之间并不完全一致，因此可以通过空间聚类提高信噪比和信号可靠性。为了避免解释孤立的通道，对每个被试在属于左、中、右三个感兴趣区域(ROI)的信号进行平均(图2b)。因此，与四个最左边的长通道(A，B，C，D)相关联的信号产生相应的Sshallow，Sdeep和Sclean的三组平均值。对中间(E，F，G，H)和最右侧(I，J，K，L)四个长通道进行同样的处理。因此，三个ROI中的每一个现在都减少到只有三个平均信号，接下来用SS(shallow)，DS(deep)和CS(clean)表示。所有的进一步处理都是对这些信号进行的，这显示出三个ROI之间的可比信噪比，因为它们是通过平均每个前极区域相同数量的相邻信号获得的。对于每个ROI，研究者计算了三个信号在所有被试中的HbO和HbR的平均时间过程。此外，还得到了相对于开始时间在−15到30s之间的试次的总平均值(10个试次×20个被试=200个试次)，计算了平均标准误差(SEM)。

2.5任务诱发频率的识别

首先通过评估任务期和基线期每个被试的NIRS数据的功率谱密度(PSD)，以此来评估任务是否成功引发了振荡。利用Welch的平均周期图法计算PSD，汉明窗长度为2000个样本，重叠50%，以获得良好的频率分辨率(0.005 Hz)，光谱平滑，并降低噪声方差。为了便于比较，通过计算每个频率窗口与整个频谱总功率之比，将PSD归一化为相对百分比值。为了进一步分析，将重点放在0.005到0.08 Hz的频率范围内，假设预期的任务诱发振荡将落在这个范围内。

沿着频率窗口进行单尾配对t检验，以检查被试内部的PSD值是否比基线高。基于聚类的非参数方法，对多重比较的t统计量进行了校正。通过Monte Carlo聚类测试计算了相同t检验的1000种排列，其中条件，即任务和基线，为被试内随机排布。然后，根据具有比观测值更大的聚类统计量的随机实现的比例来估计p值。设置临界alpha水平=0.01来识别在任务中显示显著较高PSD值的频率窗口。最后，对被试(N=20)求平均PSD，以获得每种信号类型和ROI的HbO和HbR的平均归一化PSD。此外，通过bootstrapping（自举法）使用超过1000个重采样来计算每个频率窗口平均值的95%置信区间(CI)。

2.6 SS和DS关系

SS数据是从探索额极区域的fNIRS通道获得的，源探测器距离为14mm。与大部分外侧额叶区域相比，该区域的头皮-皮层距离增加（15mm至17mm），这与额窦的存在一起降低了大脑fNIRS的敏感性。此外，源探测器距离在14到16mm之间的短通道对大脑的灵敏度仅为0.47%。虽然SS不太可能获取到皮层信号，但检验SS和DS之间的共性和差异仍很重要，以合理地确保SS数据主要由浅层血流动力学控制，而DS也包含可能来自皮质层的深层成分。该分析的基本原理是，如果DS信号中出现另一个深层振荡过程（如神经血管反应），则连接通路SS-DS将在任务频率下发生改变。为此，对于时间序列对HbOss/HbOds和HbRss/HbRds，进行了以下被试内分析：（i）用交叉来识别共同的波动，（ii）频域相关性以确定显著的协变量，以及（iii）传递函数以评估幅度和相位的关系。根据传递函数分析的建议，既不使用去趋势化，也不使用高通滤波，并对自动光谱和交叉光谱应用三角平滑窗口（系数¼、½、¼）。

为了识别浅层和深层信号之间的频域同步性（或共同波动），进行了交叉谱分析以比较这两个信号。基于Welch的平均周期图方法，使用MATLAB函数“CPSD”计算了二元时间序列的交叉功率谱密度（CPSD）；为PSD设置了长度为2000个样本和50%重叠的汉明窗。从复值结果中获得了幅值和相位值，以找到特定频率下两个信号之间的共享功率和相移。采用与第2.5节PSD相同的方法定位任务期间显示出显著较高值的峰值；以相同的方式对值进行归一化和平均。

为了确保交叉谱估计的可靠性，研究者评估了信号在特定频率下的相对振幅和相位是否有显著的稳定性。通过计算作为PSD和CPSD函数的幅度平方相干（MSC）来估计它们的频域相关性。

相干值在0（无相关性）和1（完全相关性）之间变化，描述了频域中两个信号之间的线性关系。对每个信号对和ROI的相干值进行平均。只有存在显著的相干性时，交叉谱估计才有意义。通常，0.5的值被视为显著性阈值，但由于阈值可能取决于频率，评估显著性的更好的方法是替代数据法。研究者选择了保存了原始信号的功率谱的FT1替代法。FT1替代法是通过将原始信号的傅里叶变换相位替换为[−π、π]范围内的随机值来构建的，同时保留模数，然后通过傅里叶逆变换返回时域。生成1000个替代序列，计算每个替代序列原始信号的平均MSC，实现了零假设，即平均MSC来自以实验信号相同频率异步波动的信号对。随后将从实际信号中获得的平均MSC值与FT1分布进行比较，以估计α=0.05时每个频率窗口的MSC阈值水平。

传递函数描述了系统输出信号和输入信号之间的动态关系。在此研究中，假设SS的能量在感兴趣的频率范围内，并且包含准周期振荡，则传递函数H（ƒ）根据实验fNIRS数据近似为

对于每个时间序列对，浅信号和深信号分别是用于获得特定频率下传递函数近似值的输入和输出数据（输入HBOss，输出HbOds）。从复值结果中得到了幅值（增加），它表示输入和输出之间在μM上的相对变化，以及携带时间耦合的相位（相位差或时滞），而相干值则表示这些测量的可靠性。在组水平上，对于每个信号对和ROI，研究者计算增益和圆形相位角的平均值；相位统计通过Matlab工具箱CircStat进行。此外，通过对2000次重采样计算了平均值周围的95%置信区间（CI）带。最后，为了评估任务是否会在被试之间产生一致的相位耦合，研究者对任务频率下的相位值进行了自举Rayleigh测试。一致耦合应该为相位值在最佳角度周围的狭窄分布。相反，信号较差的被试间同步应在整个360°圆内呈现出更均匀的分布。

2.7从传递函数估计深层成分

采用一种新方法从传递函数估计CS。假设DS只包含在SS中看到的相同波动，两个信号之间的关系应该是高度线性和相干的，只会因短通道和长通道采样的体积的微小差异而改变。因此，传递函数应在频率范围内产生相当恒定的增长值（取决于SS产生的DS功率的小数部分）和接近零的相移（同相）。此外，相干值应接近1。当DS中加入另一个振荡时，可以预期在某些频率下的增益或相位会出现一定程度的干扰。在特定频率下，循环血流动力学振荡可以近似为正弦，完全由振幅、相位和频率值定义。添加两个共同频率的正弦会产生一个频率相同但幅度或相位改变的正弦波。在本例中，如果任务在浅层和深层引起独立的循环振荡，则在任务频率下观察到的深正弦波Xds（t）将由两个贡献的正弦曲线Xss（t）和Xuk（t）之和产生，即

其中Xss（t）是观测到的浅正弦波，Xuk（t）是未知的深部成分。所有这些正弦波用振幅A，角频率ω和相位值Φ表示，因此，正弦式为：

因为它们代表共频的谐波振荡（即，ωds=ωss=ωuk=任务频率），它们不依赖于ω或t，只有在A和Φ上，可以将其转换为相量（或复数）。指数形式为：

其中

，和分别为Xds（t）、Xss（t）和Xuk（t）的相量，根据相量代数：

因此，可以通过计算与已知相量对应的两个复数的减法来估计未知分量，即：

为此，首先获得相位和振幅的相量值，如下所示：（1）指定

 ss作为“参考相量”，因此，Φss=0。（2）根据传递函数，得到了在任务频率下SS和DS之间的相位值ft，所以Φds=arg（H（ft）），表示ds相对于ss的位移。（3）通过计算ft处的均方根振幅并将其转换为正弦曲线的峰值振幅，从PSD中获得Ads，即Ads=，其中FR是频率分辨率（0.005Hz）。由于频谱泄漏，通过对频率间隔[ft-FR，ft+FR]内的PSD值求和，可以获得更好的振幅估计。（4）用同样的方法估计Ass，然后将其缩放到DS中应该达到的理论值。比例是在“基线”期间ft处传递函数的增益值，但它表示没有显著深层成分参与时，DS中存在的SS影响。因此，将Ass乘以基线增益，得出其缩放幅度。然后执行相量减法（方程式1），以获得振幅Auk和相量uk的相位Φuk。uk被转换为正弦曲线，它表示通过传递函数估计的替代CS。该程序针对每个参与者的信号进行，并计算每个ROI和发色团的平均值。

2.8模拟

为了评估通过相量估计CS的可行性，研究者使用任务期间的数据，而不是人工或基线信号，进行了真实的模拟。DS是将SS缩放至深层记录中应达到的振幅，即乘以基线期间的传递函数增益得到的。以0.033Hz的正弦波形式生成合成神经信号，振幅和相位由回归估计的平均CSs获得（振幅=0.05μM和0.04μM，HbO时滞=13s，HbR时滞=-9.5s，相对于CS来说）（见结果3.1和图4）。然后，将正弦信号添加到DS中，以构建模拟的深层信号。该程序应用于每个被试的中间ROI数据，然后对神经成分进行回归和相量估计。由于相量估计结果代表整个任务的平均值，在整个试次中取回归估计信号的平均值，以便进行被试内比较。使用真实合成信号和恢复信号之间的均方根误差（RMSE）量化神经估计的质量。用配对t检验来检验统计差异。

2.9测量HbO/HbR耦合

为了研究HbO和HbR之间的显著频域相关性，计算了它们在基线和任务条件下的MSC和CPSD。在这种情况下，研究者只对SS和CS信号感兴趣，假设DS只是前两者的线性组合。MSC和CPSD数据，以及它们的平均值和显著性阈值，通过前面的相同程序获得。从复值CPSD中提取任务频率的相位数据，以评估两个发色团之间的时间关系（时间偏移）。接下来在组水平上计算了相位角的角度均值，然后，为了评估相位角是否明显朝向首选方向，研究者应用了自举Rayleigh检验进行了2000次重采样。95%的置信区间也通过自举法进行计算。

2.10测量HbO/心率耦合

如第2.9节所述，通过MSC和CPSD研究了HbO与心率之间的关系。只使用SS信号的HbO数据，因为心率和其他信号之间的耦合可以从之前进行的其他测试中获得的结果推断出来。

3.结果

本研究分析了fNIRS信号如何在周期性心算任务中进行波动，这可能会诱发生理应激反应。为了减少可能影响结果的假定压力反应，研究者采取了以下措施：首先，使用了一个只有30s的任务持续时间，包括计算和复原阶段。其次，让被试事先练习10-15min，确保其理解实验任务。第三，被试在整个实验过程中有稳定的心理表现，且心率波动较低。实际上，实验的两种条件（基线和任务）下，他们的心率值没有显著差异（Wilcoxon符号秩检验，p=0.091）。就平均而言，在任务期间，平均心率仅略微增加，即与基线相比增加了7bpm（9%）（见表1）。

表1.被试的平均心率指标（基线和任务）。

3.1振荡与任务频率一致

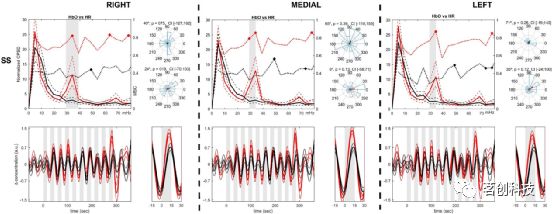
fNIRS信号显示出与任务频率一致的明显振荡，并且在浅层和深层的多个ROI上始终观测到这种振荡。图3显示了组水平PSD分析的结果。针对三个ROI中的每一个、每种信号类型和每种条件（基线和任务），对参与者的归一化PSD进行平均。DC成分（频率=0）设置为零，显示频率范围的上限值为0.08Hz。在静息状态（图3，黑线）和心理任务（图3，彩线）期间，都可以在～0.01 Hz处看到一个普遍存在的峰值，尽管聚类置换检验发现这两种条件之间没有显著差异。然而，仅在任务期间检测到ft处的清晰峰值，并通过聚类检验标记为显著（p＜.01）（图3，灰色阴影区域）。该峰值与任务频率密切相关，并在所有ROI和信号类型中可以观察到。在某些情况下，还发现0.066Hz左右的次级峰值，这很可能表示基本任务频率的谐波。显然，这项任务成功地诱发了HbO和HbR的周期性波动，这些波动出现在浅层信号（图3SS）、深层信号（图3DS）和干净信号（图3CS）中。

图3.在0.005到0.08 Hz的频率范围内，每个ROI（右、中、左）、发色团和信号类型的归一化PSD的总平均值。

图4显示了在使用0.015 Hz的滤波器宽度对任务频率范围进行带通滤波后，HbO和HbR组水平的平均时间轨迹。可以看出SSs（图4SS）是如何开始与任务试次同步振荡的，尽管在两个发色团之间显示出明显的时间偏移。图4还描述了被试试次的总平均值（时间轨迹旁边的小图），对于SS显示出一个共同的反应，包括：（i）在试次开始前不久，HbO强烈增加，在约11.2s时达到最大值，（ii）然后HbO在随后的休息期间缓慢恢复到之前的水平，（iii）HbR变化不太明显，领先HbO约4s。DSs可以观察到类似的周期性响应（图4DS），但HbO峰值略低于SS（约0.3s），而HbR滞后SS约2s。最后，CSs也显示了与任务一致的周期性波动（图4CS），但在这种情况下，HbO相对于SS以反相振荡。此外，HbO和HbR显示出相似的振幅（～0.05μM），并且彼此呈反相关，HbO在约12.6s时显示出谷值，HbR在约18.5s时显示出峰值。在这一点上，观察到的DS相对于SS的时间偏移似乎是由于CS成分的总和。有趣的是，在CS中看到倒置的HbO/HbR反应，即HbO减少，HbR增加。但倒置模式不会立即出现，会在最初的几个试次中逐渐达到稳定。这一观察结果可能有助于初步的生理解释。

图4.对于每个ROI和信号类型，参与者在任务期间的HbO（红线）和HbR（蓝线）的平均时间过程。时间进程旁边的小块显示了试次的总平均值。SEM用细线表示。灰色框表示每个试次有15s的心算时间。每行显示了三个ROI（右、中、左）的浅（SS）、深（DS）和干净信号（CS）的结果。

3.2 SS/DS关系

为了研究浅层波动在多大程度上影响深部信号，研究者在SS和DS数据之间进行了相干、交叉谱和传递函数估计（图5）。分析显示，在以ft为中心的任务期间，出现了一个显著的交叉谱峰值（p＜.01），并且存在于HbO和HbR的所有ROI中（图5a，左侧）。这些峰值表明，SS和DS在任务频率上振荡，具有显著的同步功率。此外，有一个较高的峰值位于约0.01Hz处，但与基线相比，任务期间无显著差异。

在这两种条件下，整个探测频率范围的相干值均高于显著性阈值（图5a，右侧图），描述了频域中SS和DS之间的一致线性关系。HbO的相干性水平很高（平均＞0.8），表明相关性更强，并且HbO可能比HbR更受浅层血流动力学的影响。应该注意的是，相干性在ft前后的任务中也达到峰值（在HbR上非常明显），这意味着任务诱发的振荡比自发振荡更相干。

在任务期间，传递函数分析显示HbO在ft左右的幅度下降，尤其是在中间ROI（图5b）。相位值在相同频率下也显示出一定的扰动（图5c）。HbR表现出轻微的幅度增加，主要在中间和左侧ROI中可以观察到（图5b），同时相位值出现强烈干扰（图5c）。同样，静息状态下没有显示出这种变化。t检验显示，休息期间的HbO和HbR的增益值在组水平上没有差异（p=0.2）。然而，在任务期间，中间和左侧ROI中HbO的增益值明显较低（p＜.01），这与图5b中显示的增益值下降一致。在比较任务与休息条件时，配对t检验显示出HbO或HbR没有差异，这表明就平均而言，任务期间的变化非常细微。

圆形直方图显示，在静息态期间，所有情况下的相位角集中在任务频率的0°左右（图5g）。这意味着SS和DS在该频率下几乎同相振荡（无时滞）。然而，在任务期间，中间和左侧ROI的HbR相位分别明显移向正值（DS滞后于SS）22°和30°，对应于时间滞后1.8和2.5s的ft（图5d）。HbO的相位变化不如HbR明显，在相同的ROI中观察到轻微的负值偏移（DS快于SS）。值得注意的是，从相位值计算的时滞与从平均时间序列获得的时滞一致（见图4）。

正如预期那样，这些结果证了实浅层和深层信号高度相关，突出表层血流动力学对深层记录的强烈影响，这对于HbO尤其如此。分析还揭示了与任务相关的幅值和相位变化，指出了DS中唯一存在的深层成分的贡献，它负责观测到的干扰。因此，这些发现证实了深层记录捕捉到了其他不同于表层的振荡过程。

图5.CPSD、MSC被试的平均结果以及每个ROI的SS和DS之间的传递函数数据、比较基线期和任务期。

3.3传递函数的神经信号估计

研究者采用另一种方法，通过使用从传递函数获得的幅值和相位数据的相量表示来估计假定的神经信号。假设信号在任务确定的排序周期内是平稳的情况下，为其建模在0.033 Hz（即任务频率）下振荡的正弦曲线。相量代数用于提取解释DS中观察到的扰动的隐藏深层成分。图6比较了通过回归获得的CS与通过中间ROI中的传递函数数据估计的CS。如第3.2节所述，HbO的传递函数显示出在ft左右的幅度明显下降，同时相移约为−8°，如图6a中间图所示。左图显示了实验获得的试次的总平均值，比较了SS（实线）和DS（虚线）。可以看到DS的振幅较小，相对于SS向左侧轻微移动。右图显示了在没有任何其他干扰成分的情况下，根据静息态得到的幅度估计值，SS在DS中应该是什么样子。如红色箭头所示，与预测SS（实线）相关的观测DS（虚线）的幅值和相位差现在更加明显。

执行相量减法后，干扰深层成分显示为图6c右侧图中红色迹线所示的正弦曲线。HbR中，在ft处测量到微小增加的幅度和大约22°的相移。类似地，图6b的右图说明了预测（实线）和观察（虚线）DS之间的差异。相量代数指出图6c右侧绘制的蓝色正弦曲线是造成干扰的原因。图6c的左图显示了通过回归获得的CSs。可以看出，它与相量估计的深层成分非常匹配。对于三个ROI（右、中、左），HbO的SS和CS之间的估计时滞平均为11.5、13和10.7s，而HbR为−9.9、，−9.5和−9.5s。相量分析证实，这项任务以倒置的HbO/HbR反应的形式诱发了深部血流动力学波动，研究者将其视为正在寻找的神经信号。考虑到被试之间的个体差异和可变性，还是发现90%的被试（n=18）在至少一个ROI中表现出这种类型的反应。

图6.在中间ROI中，通过回归和相量分析对神经信号估计进行比较的示意图。

3.4模拟结果

图7a显示了被试的每个发色团的带通滤波SS、模拟DS和合成神经响应的一部分。对于每种估计方法，所有被试的平均恢复信号如图7b所示。在HbO的情况下，可以看出，两种方法的恢复信号的形状非常相似，但相量更适合真实的合成信号，显示出显著较低的RMSE值。HbR时间过程也具有可比性，但相量的表现也更好。

这些发现表明，与相量相比，回归降低了振幅（主要是HbO的振幅）。本研究发现HbO的SS-DS相干性高于HbR，表明回归性能可能会受到强相关性的影响。总的来说，相量法似乎与回归法一样好，甚至比回归法更好，并且在任何情况下都有助于独立地验证结果。

图7.构建合成数据和模拟结果。

3.5 HbO/HbR耦合

在任务期间，CPSD在所有ROI的SS（图8SS，左轴，红色迹线）和CS（图8CS，左轴，红色迹线）的ft处显示出明显的同步功率峰值。MSC测量结果显示在多个频率下存在显著的频域相关水平。还可以看出，任务期间（红色迹线）的MSC水平高于静息状态（黑色迹线），这表明任务不仅在频率上增加了耦合，而且在频率之外也增加了耦合。

MSC也在ft左右达到峰值，在中间和左侧ROI达到最高水平，这表明HbO和HbR之间有很强的相关性。关于SS的时间耦合，圆形直方图显示了ft处的相位差在任务期间显著集中在右侧、中间和左侧ROI的-39°、-39°和 -47°上（图8SS，底部圆形图）。对于基线数据，相位分析对任何ROI都不显著（图8SS，顶部的圆形图）。但CS显示，平均后HbO和HbR在中间和左侧ROI中几乎呈反相振荡，显示时间延迟约为15s，但优先级不明确。在右侧ROI中，在任何情况下都没有达到显著性水平。这些结果表明，该任务在浅层和深层引起HbO和HbR之间的相干波动，但存在一些差异。对于SS，被试在所有ROI上的时间耦合是一致的。然而，组水平上的CS相位仅在中间和左侧区域是一致的，而且显示出反相波动，与反向血流动力学反应一致。

图8.每个ROI的平均CPSD、MSCs以及HbO和HbR之间相位、比较基线期和任务期。

3.6 HbO/心率耦合

CPSD和MSC测量也用于研究HbO和心率耦合。这里只关注浅层信号中的显著峰值。如图9所示，同步功率的峰值位于三个ROI中的ft处。同时，MSC在相同频率下也达到峰值，表明在任务频率下有很强的相关性。但在任何情况下，相位平均值均未达到显著水平。这些结果表明，在单一被试水平上，HbO和心率振荡耦合良好，使得平均后的组水平上有显著一致性。然而，各个相位值的差异足以分散角度平均值，这反映出两个信号在时间耦合上存在明显的被试间差异。图9还显示了带通滤波HbO（底图，红线）和心率（底图，黑线）的平均波动。被试间试次的总平均值（时间进程旁边的小图）也显示，这两种信号在试次开始前几秒钟开始增加。

图9.每个ROI的平均时间进程、CPSD、MSCs以及表层HbO和心率(HR)之间的相位、比较基线期和任务期。

4.结论

本研究的主要目的是：评估使用节律性认知任务，来诱发适用于有效频率分辨测量的周期性血流动力学波动的可行性。首先研究了功率谱分析是否可以区分任务期和休息期。接下来，测量了不同信号对之间的相位-振幅耦合，以估计其线性关系，旨在区分功能性脑反应和脑外混杂因素，并推断潜在过程的性质。

心算任务成功地诱发了前额区域测量到的NIRS信号的周期性变化，表现为以任务频率（即0.033Hz）为中心的高度特征谱峰。这些峰值明显可从静息状态下的自发活动中辨别出来，并且明显与压力反应无关。由于心算任务经常被用作压力源，而心理超负荷会增加压力，这里使用的实验方案是为了尽量减少这种影响而定制的。

本研究证实了表面血流动力学对深层fNIRS信号的强烈影响，这反映在从多距离记录获得的信号之间的高相干水平上。利用任务施加的同步振荡状态来提取振幅和相位数据，并使用它来分离真实的深层信号和来自脑外组织的信号。但提取的深部信号遵循一种不寻常的模式，即HbO减少和HbR增加，这与典型的大脑激活反应是相反的。总而言之，本次研究结果表明，在额叶区域，深层信号受到表层活动的强烈影响。事实上，如果只分析深层信号而不进行适当的校正，则可能错误地推断出任务诱发的激活反应。当只考虑HbO时，更有可能发生这种错误。

原文：Frequency-domain analysis of fNIRS fluctuations induced by rhythmic mental arithmetic.

https://doi.org/10.1111/psyp.14063

​文章来源于微信公众号（茗创科技），欢迎有兴趣的朋友搜索关注。