深度学习4大激活函数

如果不用激励函数（其实相当于激励函数是f(x) = x），在这种情况下你每一层输出实际上都是上层输入的线性函数。

这样就使得无论神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，模型的表达力仍然不够。

我们决定引入非线性函数作为激励函数，这样深层神经网络才有意义（不再是输入的线性组合）。

本文将介绍深度学习中的4个常见的激活函数，从原函数公式、导数函数及二者的可视化来进行对比：

• Sigmoid函数
• Tanh函数
• ReLu函数
• Leaky ReLu函数

激活函数特征

1. 非线性：激活函数满足非线性时，才不会被单层网络替代，神经网络才有了意义
2. 可微性：优化器大多数是用梯度下降来更新梯度；如果不可微的话，就不能求导，也就不能更新参数
3. 单调性：激活函数是单调的，能够保证网络的损失函数是凸函数，更容易收敛

Sigmoid函数

表示形式为tf.nn.sigmoid(x)

$$f(x)=\frac{1}{1+e^{-x}}$$

原函数

In [1]:

# import tensorflow as

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
 

def sigmoid(x):
    """
    返回sigmoid函数
    """
    return 1 / (1 + np.exp(-x))

 
def plot_sigmoid():
    # param:起点，终点，间距
    x = np.arange(-10, 10, 0.2)
    y = sigmoid(x)
    plt.plot(x, y)
    plt.grid()
    plt.show()
 
 
if __name__ == '__main__':
    plot_sigmoid()

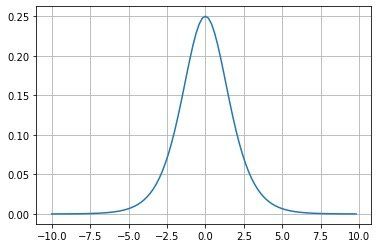
导数函数

该函数的导数为：

$$\begin{array}{rl}{f}^{\prime }(z)& ={\left(\frac{1}{1+e^{-z}}\right)}^{\prime }\\ & =\frac{e^{-z}}{{\left(1+e^{-z}\right)}^2}\\ & =\frac{1+e^{-z}-1}{{\left(1+e^{-z}\right)}^2}\\ & =\frac{1}{\left(1+e^{-z}\right)}\left(1-\frac{1}{\left(1+e^{-z}\right)}\right)\\ & =f(z)(1-f(z))\end{array}$$

另一种求解方法：

步骤1：

$$\begin{array}{rl}\frac{\mathrm{d}y}{\mathrm{d}x}& =-{\left(1+e^{-x}\right)}^{-2}\cdot {\left(1+e^{-x}\right)}^{\prime }\\ & =-{\left(1+e^{-x}\right)}^{-2}\cdot 1\cdot {\left(e^{-x}\right)}^{\prime }\\ & =-{\left(1+e^{-x}\right)}^{-2}\cdot 1\cdot \left(e^{-x}\right)\cdot (-x{)}^{\prime }\\ & =-{\left(1+e^{-x}\right)}^{-2}\cdot 1\cdot \left(e^{-x}\right)\cdot (-1)\\ & ={\left(1+e^{-x}\right)}^{-2}\cdot \left(e^{-x}\right)\\ & =\frac{e^{-x}}{{\left(1+e^{-x}\right)}^2}\end{array}$$

步骤2：

$$1-y=1-\frac{1}{1+e^{-x}}=\frac{1+e^{-x}-1}{1+e^{-x}}=\frac{e^{-x}}{1+e^{-x}}$$

步骤3：

$$\frac{dy}{dx}=\frac{e^{-x}}{(1+e^{-x})}\ast \frac{1}{(1+e^{-x})}=y(1-y)$$

# import tensorflow as

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
 

def der_sigmoid(x):
    """
    返回sigmoid函数
    """
    sig = 1 / (1 + np.exp(-x))  # sigmoid函数
    
    return sig * (1 - sig)  # 输出为导数函数

 
def plot_der_sigmoid():
    # param:起点，终点，间距
    x = np.arange(-10, 10, 0.2)
    y = der_sigmoid(x)  # 导数函数
    plt.plot(x, y)
    plt.grid()
    plt.show()
 
 
if __name__ == '__main__':
    plot_der_sigmoid()

特点

Sigmoid函数是二分类算法，尤其是逻辑回归中算法中的常用激活函数；也可以作为较少层数的神经网络的激活函数。

它主要是有下面几个特点：

1. 能够将自变量∈的值全部缩放到(0,1)之间。
2. 当X无穷大的时候，函数值趋于1；X无穷小的时候，趋于0。相当于对输入进行了归一化操作。
3. 该函数是一个连续可导的函数；通过导数函数的图像能够观察到：0点时候，导函数的值最大，并且两边逐渐减小

缺陷

• 从导数函数的图像中观察到，X在正无穷大或者负无穷小的时候，导数（梯度）为0，即出现了梯度弥散现象；
• 导数的值在(0,0.25)之间；在多层神经网络中，我们需要对输出层到输入层逐层进行链式求导。这样就导致多个0到0.25之间的小数相乘，造成了结果取0，造成了梯度消失。
• Sigmod函数存在幂运算，计算复杂度大，训练时间长。

下面解释下Sigmoid最为致命的缺点（参考一位网友的回答，解释很全面）

对于Sigmoid激活函数最致命的缺点就是容易发生梯度弥散（Gradient vanishing）现象（当然也可能会发生梯度爆炸Exploding gradient，前面层的梯度通过模型训练变的很大，由于反向传播中链式法则的原因，导致后面层的梯度值会以指数级增大。 但是在Sigmoid激活函数中梯度保障发生的概率非常小），所谓梯度弥散故名思议就是梯度值越来越小。

在深度学习中，梯度更新是从后向前更新的，这也就是所谓的反向传播（Backpropagation algorithm），而反向传播的核心是链式法则。如果使用Sigmoid激活函数，训练的网络比较浅还比较好，但是一旦训练较深的神经网络，会导致每次传过来的梯度都会乘上小于1的值，多经过几层之后，梯度就会变得非常非常小（逐渐接近于0），因此梯度消失了，对应的参数得不到更新。

参考：https://zhuanlan.zhihu.com/p/104318223

现在神经网络中很少使用Sigmoid作为激活函数。

tanh函数

tanh 是一个双曲正切函数。tanh 函数和 sigmoid 函数的曲线相似。

该函数是一个奇函数，经过原点且严格单调递增。函数取值分布在(-1,1)之间。

原函数

下面是原函数的具体表达形式，我们还发现tanh函数和sigmoid函数的关系：

$$\tanh x=\frac{\sinh x}{\cosh x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{1-e^{-2x}}{1+e^{-2x}}=2\ast Sigmoid(2\ast x)-1$$

import math
import matplotlib.pyplot as plt
import numpy as np
import matplotlib as mpl


def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111)

x = np.linspace(-10, 10)
y = tanh(x)

ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data', 0))
ax.set_xticks([-10, -5, 0, 5, 10])
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.set_yticks([-1, -0.5, 0.5, 1])

plt.plot(x, y, label="Tanh", color="red")
plt.legend()
plt.grid()
plt.show()

导函数

下面是具体的求导过程：

$$f(x)=\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

首先公布结果，导数函数为：

$$f(x{)}^{\prime }=1-(\tanh (x){)}^2$$

下面是具体过程：

步骤1、在除法的求导公式中有：

$${\left(\frac{\mu }{\nu }\right)}^{\prime }=\frac{{\mu }^{\prime }\nu -\mu {\nu }^{\prime }}{{\nu }^2}$$

步骤2、定义两个中间变量：

$$a=e^x$$

$$b=e^{-x}$$

步骤3、第一次求导

$${\left(\frac{e^x-e^{-x}}{e^x+e^{-x}}\right)}^{\prime }={\left(\frac{a-b}{a+b}\right)}^{\prime }=\frac{(a-b{)}^{\prime }\times (a+b)-(a-b)\times (a+b{)}^{\prime }}{(a+b{)}^2}$$

步骤4、其中有

$$(a-b{)}^{\prime }=\left(e^x-e^{-x}\right)=e^x-(-1)\times e^{-x}=e^x+e^{-x}$$

$$(a+b{)}^{\prime }=\left(e^x+e^{-x}\right)=e^x+(-1)\times e^{-x}=e^x-e^{-x}$$

步骤5、将a+b和a-b进行整理：

$$(a-b{)}^{\prime }=e^x+e^{-x}=a+b$$

$$(a+b{)}^{\prime }=e^x-e^{-x}=a-b$$

步骤6、化简上面的结果

$$\begin{array}{l}\frac{(a-b{)}^{\prime }\times (a+b)-(a-b)\times (a+b{)}^{\prime }}{(a+b{)}^2}\\ =\frac{(a+b{)}^2-(a-b{)}^2}{(a+b{)}^2}\\ =1-\frac{(a-b{)}^2}{(a+b{)}^2}\\ =1-{\left(\frac{e^x-e^{-x}}{e^x+e^{-x}}\right)}^2\\ =1-\tanh (x{)}^2\end{array}$$

# 绘制图

import math
import matplotlib.pyplot as plt
import numpy as np
import matplotlib as mpl


def der_tanh(x):
    """
    tanh(x)函数的导数求解
    """
    tanh = (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
    
    return 1-tanh ** 2

fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111)

x = np.linspace(-10, 10)
y = der_tanh(x)

ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data', 0))
ax.set_xticks([-10, -5, 0, 5, 10])
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.set_yticks([-1, -0.5, 0.5, 1])

plt.plot(x, y, label="der_tanh", color="red")
plt.legend()
plt.grid()
plt.show()

特点

1. Tanh函数输出满足0均值；
2. 当输入较大或者较小时，输出的值变化很小，导致导函数几乎为0，也就是梯度很小，从而不利于W、b的值更新（二者的更新都和梯度有关）。
3. 梯度（导数）的取值在（0，1]之间，最大梯度为1，能够保证梯度在变化过程中不削减，缓解了Sigmoid函数梯度消失的问题；但是取值过大或者过小，仍存在梯度消失
4. 同样地函数本身存在幂运算，计算力度大

Sigmoid和Tanh关系

# encoding:utf-8

import math
import matplotlib.pyplot as plt
import numpy as np
import matplotlib as mpl
mpl.rcParams['axes.unicode_minus']=False
 
def  sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))
 
fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(111)
 
x = np.linspace(-10, 10)

# sigmoid函数
y = sigmoid(x)
# tanh函数
tanh = 2*sigmoid(2*x) - 1
 
plt.xlim(-11,11)
plt.ylim(-1.1,1.1)
 
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
 
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.set_xticks([-10,-5,0,5,10])
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
ax.set_yticks([-1,-0.5,0.5,1])
 
plt.plot(x,y,label="Sigmoid",color = "blue")
# tanh函数这里是2*x
plt.plot(2*x,tanh,label="Tanh", color = "red")
plt.legend()
plt.grid()
plt.show()

在一般的二分类问题中，Sigmoid函数一般用输出层，而tanh函数一般用于隐藏层（非固定，经验之谈）。

Relu函数

ReLu函数是目前深度学习中比较流行的一种激活函数。

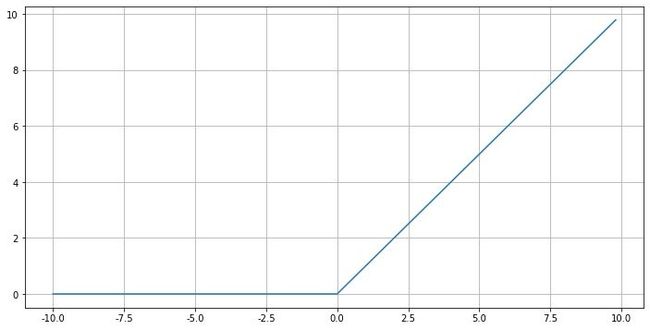
原函数

ReLU函数, 也称之为线性整流函数(Rectified Linear Unit), 是神经网络结构中常用的非线性激活函数。下面是简写形式：

$$f(x)=max(x,0)$$

下面是完整的表达式：

$$\mathrm{ReLU}(x)=\{\begin{array}{ll}0,& x⩽0\\ x,& x>0\end{array}$$

# import tensorflow as tf

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
 

def relu(x):
    """
    返回Relu函数
    """
    # 不能直接使用max函数，报错
    return np.maximum(0, x)  

 
def plot_relu():
    # param:起点，终点，间距
    plt.figure(figsize=(12,6))
    x = np.arange(-10, 10, 0.2)
    y = relu(x)  # 导数函数
    plt.plot(x, y)
    plt.grid()
    plt.show()
 
 
if __name__ == '__main__':
    plot_relu()

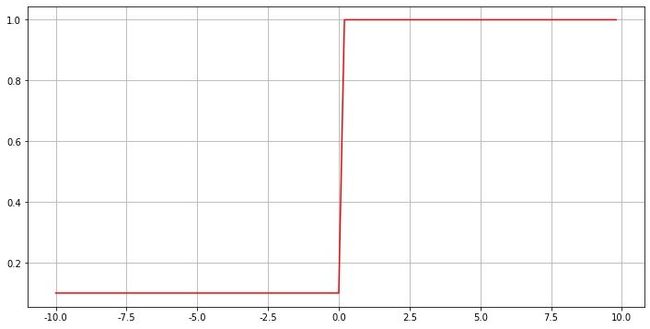
导数函数

$$y^{\prime }=f^{\prime }(x)=\{\begin{array}{ll}1,& x>0\\ 0,& x\le 0\end{array}$$

# import tensorflow as tf

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
 

def der_relu(x):
    """
    返回Relu导数函数
    """
    # 重点：通过numpy的where函数进行判断
    return np.where(x>0,1,0)   

 
def plot_der_relu():
    # param:起点，终点，间距
    plt.figure(figsize=(12,6))
    x = np.arange(-10, 10, 0.2)
    y = der_relu(x)  # 导数函数
    plt.plot(x, y)
    plt.grid()
    plt.show()
 
 
if __name__ == '__main__':
    plot_der_relu()

特点

1. 函数本身在输入大于为0的时候，输出逐渐增加，这样梯度值也一直存在，从而避免了梯度的饱和：正区间解决梯度消失问题
2. 函数本身是线性函数，比Sigmoid或者Tanh函数要计算速度快；同时函数的收敛速度要大于Sigmoid或者Tanh函数
3. 函数的输出不是以0为均值，收敛慢
4. Dead Relu问题：在负输入部分，输入的值为0，从而梯度为0，导致参数无法更新，造成神经元死亡；在实际处理中，我们可以减少过多的负数特征进入网络

Leaky ReLu 函数

Leaky ReLu 函数是为了解决Relu函数负区间的取值为0而产生的。

• 左：ReLu
• 右：Leaky ReLu

原函数

在小于0的部分引入了一个斜率，使得小于0的部分取值不再全部是0（通常 a 的值为 0.01 左右）

$$y=f(x)=\{\begin{array}{ll}x,& x>0\\ a\cdot x,& x\le 0\end{array}$$

# import tensorflow as tf

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
 

def leaky_relu(x):
    """
    返回Leaky Relu函数图像
    """ 
    a = 0.01  # 斜率a的取值
    return np.maximum(a * x, x)  # 通过np.maximum函数实现

 
def plot_Leaky_relu():
    # param:起点，终点，间距
    plt.figure(figsize=(12,6))
    x = np.arange(-10, 10, 0.2)
    y = leaky_relu(x)  # 导数函数
    plt.plot(x, y, color="red")
    plt.grid()
    plt.show()
 
 
if __name__ == '__main__':
    plot_Leaky_relu()

导数函数

$$y‘=f‘(x)=\{\begin{array}{ll}1,& x>0\\ a,& x\le 0\end{array}$$

# import tensorflow as tf

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
 

def der_leaky_relu(x):
    """
    返回Leaky Relu函数图像
    """ 
    # 斜率a的取值
    a = 0.1  
    # 通过where判断来取值
    return np.where(x>0,1,a)  

 
def plot_Leaky_relu():
    # param:起点，终点，间距
    plt.figure(figsize=(12,6))
    x = np.arange(-10, 10, 0.2)
    y = der_leaky_relu(x)  # 导数函数
    plt.plot(x, y, color = "red")
    plt.grid()
    plt.show()
 
 
if __name__ == '__main__':
    plot_Leaky_relu()

特点

1. 具有和ReLu完全相同的特点，而且不会造成Dead ReLu问题
2. 函数本身的取值在负无穷到正无穷；负区间梯度也存在，从而避免了梯度消失。
3. 但是实际运用中，尚未完全证明 Leaky ReLU 总是比 ReLU 更好。