萌新待开发
萌新待开发

进阶篇

目录

模型实用技巧

特征提升

特征抽取

特征筛选

模型正则化

欠拟合与过拟合

L1范数正则化

L2范数正则化

模型检测

留一验证

交叉验证

超参数搜索

网格搜索​

并行搜索

流行库/模型实践

自然语言处理包（NLTK）

词向量(Word2Vec)技术

XGBoost模型

Tensorflow框架

模型实用技巧

特征提升

进阶篇_第1张图片

特征抽取

进阶篇_第2张图片

DicVectorizer对使用字典存储的数据进行特征抽取与向量化

#定义一组字典列表，用来表示多个数据样本（每个字典代表一个数据样本）
measurements = [{'city':'Dubai','temperature':33.},{'city':'London','temperature':12.},{'city':'San Fransisco','temperature':18.}]
#从 sklearn.feature_extravtion 导入 DictVectorizer
from sklearn.feature_extraction import DictVectorizer
#初始化 DictVectorizer 特征抽取器
vec = DictVectorizer()
#输出转化之后的特征矩阵
print(len(measurements))
print(vec.fit_transform(measurements))
print(vec.fit_transform(measurements).toarray())
#输出各个维度的特征含义
print(vec.get_feature_names())

结果：
3
  (0, 0)	1.0
  (0, 3)	33.0
  (1, 1)	1.0
  (1, 3)	12.0
  (2, 2)	1.0
  (2, 3)	18.0
[[ 1.  0.  0. 33.]
 [ 0.  1.  0. 12.]
 [ 0.  0.  1. 18.]]
['city=Dubai', 'city=London', 'city=San Fransisco', 'temperature']

进阶篇_第3张图片

使用 CountVectorizer 并且不去掉停用词的条件下，对文本特征进行量化的朴素贝叶斯分类性能测试

#从 skearn.datasets 里导入20类新闻文本数据抓取器
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report

#从互联网上即使下载新闻样本，subset='all'参数代表下载全部近2万条文本存储在变量news中
news = fetch_20newsgroups(subset='all')
#从 sklearn.model_selection 导入 train_test_split 模块用于分割数据集
#对 news 中的数据 data 进行分割，25%的文本用作测试集，75%作为训练集
X_train,X_test,y_train,y_test = train_test_split(news.data,news.target,test_size=0.25,random_state=33)

#从 sklearn.feature_extraction.text 里导入 CountVectorizer
#采用默认的配置对 CountVectorizer 进行初始化（默认配置不去除英文停用词），并且赋值给变量 count_vec
cout_vec = CountVectorizer()

#只使用词频率统计的方式将原始训练和测试文本转化为特征向量
X_count_train = cout_vec.fit_transform(X_train)
X_count_test = cout_vec.transform(X_test)
#从 sklearn.naive_bayes 里导入朴素叶贝斯分类器
#使用默认的配置对分类器进行初始化
mnb_count = MultinomialNB()
#使用朴素叶贝斯分类器，对 CountVectorizer(不去除停用词)后的训练样本进行参数学习
mnb_count.fit(X_count_train,y_train)

#输出模型准确性结果
print("The accuracy of classifying 20newsgroups using Naive Bayes (CountVecorizer without filtering stopwords):",mnb_count.score(X_count_test,y_test))
#将分类预测的结果存储在变量 y_zount_predict 中
y_count_predict = mnb_count.predict(X_count_test)
#从 sklearn.metrics 导入 classification_report
#输出更加详细的其他评价分类性能的指标
print(classification_report(y_test,y_count_predict,target_names=news.target_names))

结果：
The accuracy of classifying 20newsgroups using Naive Bayes (CountVecorizer without filtering stopwords): 0.8397707979626485
                          precision    recall  f1-score   support

             alt.atheism       0.86      0.86      0.86       201
           comp.graphics       0.59      0.86      0.70       250
 comp.os.ms-windows.misc       0.89      0.10      0.17       248
comp.sys.ibm.pc.hardware       0.60      0.88      0.72       240
   comp.sys.mac.hardware       0.93      0.78      0.85       242
          comp.windows.x       0.82      0.84      0.83       263
            misc.forsale       0.91      0.70      0.79       257
               rec.autos       0.89      0.89      0.89       238
         rec.motorcycles       0.98      0.92      0.95       276
      rec.sport.baseball       0.98      0.91      0.95       251
        rec.sport.hockey       0.93      0.99      0.96       233
               sci.crypt       0.86      0.98      0.91       238
         sci.electronics       0.85      0.88      0.86       249
                 sci.med       0.92      0.94      0.93       245
               sci.space       0.89      0.96      0.92       221
  soc.religion.christian       0.78      0.96      0.86       232
      talk.politics.guns       0.88      0.96      0.92       251
   talk.politics.mideast       0.90      0.98      0.94       231
      talk.politics.misc       0.79      0.89      0.84       188
      talk.religion.misc       0.93      0.44      0.60       158

                accuracy                           0.84      4712
               macro avg       0.86      0.84      0.82      4712
            weighted avg       0.86      0.84      0.82      4712

进阶篇_第4张图片

使用 TfidfVectorizer并且不去掉停用词的条件下，对文本特征进行量化的朴素贝叶斯分类性能测试

#从 skearn.datasets 里导入20类新闻文本数据抓取器
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report

#从互联网上即使下载新闻样本，subset='all'参数代表下载全部近2万条文本存储在变量news中
news = fetch_20newsgroups(subset='all')
#从 sklearn.model_selection 导入 train_test_split 模块用于分割数据集
#对 news 中的数据 data 进行分割，25%的文本用作测试集，75%作为训练集
X_train,X_test,y_train,y_test = train_test_split(news.data,news.target,test_size=0.25,random_state=33)

#从 sklearn.feature_extraction.text 里导入 TfidfVectorizer
#采用默认的配置对 TfidfVectorizer 进行初始化（默认配置不去除英文停用词），并且赋值给变量 count_vec
tfidf_vec = TfidfVectorizer()

#只使用词频率统计的方式将原始训练和测试文本转化为特征向量
X_tfidf_train = tfidf_vec.fit_transform(X_train)
X_tfidf_test = tfidf_vec.transform(X_test)
#从 sklearn.naive_bayes 里导入朴素叶贝斯分类器
#使用默认的配置对分类器进行初始化
mnb_tfidf = MultinomialNB()
#使用朴素叶贝斯分类器，对 TfidfVectorizer(不去除停用词)后的训练样本进行参数学习
mnb_tfidf.fit(X_tfidf_train,y_train)

#输出模型准确性结果
print("The accuracy of classifying 20newsgroups using Naive Bayes (TfidfVectorizer without filtering stopwords):",mnb_tfidf.score(X_tfidf_test,y_test))
#将分类预测的结果存储在变量 y_zount_predict 中
y_tfidf_predict = mnb_tfidf.predict(X_tfidf_test)
#从 sklearn.metrics 导入 classification_report
#输出更加详细的其他评价分类性能的指标
print(classification_report(y_test,y_tfidf_predict,target_names=news.target_names))

结果：
The accuracy of classifying 20newsgroups using Naive Bayes (TfidfVectorizer without filtering stopwords): 0.8463497453310697
                          precision    recall  f1-score   support

             alt.atheism       0.84      0.67      0.75       201
           comp.graphics       0.85      0.74      0.79       250
 comp.os.ms-windows.misc       0.82      0.85      0.83       248
comp.sys.ibm.pc.hardware       0.76      0.88      0.82       240
   comp.sys.mac.hardware       0.94      0.84      0.89       242
          comp.windows.x       0.96      0.84      0.89       263
            misc.forsale       0.93      0.69      0.79       257
               rec.autos       0.84      0.92      0.88       238
         rec.motorcycles       0.98      0.92      0.95       276
      rec.sport.baseball       0.96      0.91      0.94       251
        rec.sport.hockey       0.88      0.99      0.93       233
               sci.crypt       0.73      0.98      0.83       238
         sci.electronics       0.91      0.83      0.87       249
                 sci.med       0.97      0.92      0.95       245
               sci.space       0.89      0.96      0.93       221
  soc.religion.christian       0.51      0.97      0.67       232
      talk.politics.guns       0.83      0.96      0.89       251
   talk.politics.mideast       0.92      0.97      0.95       231
      talk.politics.misc       0.98      0.62      0.76       188
      talk.religion.misc       0.93      0.16      0.28       158

                accuracy                           0.85      4712
               macro avg       0.87      0.83      0.83      4712
            weighted avg       0.87      0.85      0.84      4712

进阶篇_第5张图片

特征筛选

进阶篇_第6张图片

#导入 pandas 并且更名为pd
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier
from sklearn import feature_selection
from sklearn.model_selection import cross_val_score
import numpy as np
import pylab as pl

#从互联网读入titanic 数据
#titanic = pd.read_csv('http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt')
titanic = pd.read_csv('train.csv')
#分离数据特征与预测目标
y = titanic['Survived']
X = titanic.drop(['Name','Survived'],axis=1)

#对对缺失数据进行填充
X['Age'].fillna(X['Age'].mean(),inplace = True)
X.fillna('UNKNOWN',inplace=True)

#分割数据，依然采用 25% 用于测试
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.25,random_state=33)

#类别型特征向量化
vec = DictVectorizer()
X_train = vec.fit_transform(X_train.to_dict(orient = 'records'))
X_test = vec.transform(X_test.to_dict(orient = 'records'))

#输入处理后特征向量的维度
print("处理后维度：",len(vec.feature_names_))

#使用决策树模型依靠所有特征进行预测，并作性能评估
dt = DecisionTreeClassifier(criterion='entropy')
dt.fit(X_train,y_train)
print("所有特征进行预测：",dt.score(X_test,y_test))

#从 sklearn 导入特征筛选器
#筛选前 20% 的特征，使用相同配置的决策树模型进行预测，并且评估性能
fs = feature_selection.SelectPercentile(feature_selection.chi2,percentile=20)
X_train_fs = fs.fit_transform(X_train,y_train)
dt.fit(X_train_fs,y_train)
X_test_fs = fs.transform(X_test)
print("选择前20%的特征进行预测：",dt.score(X_test_fs,y_test))

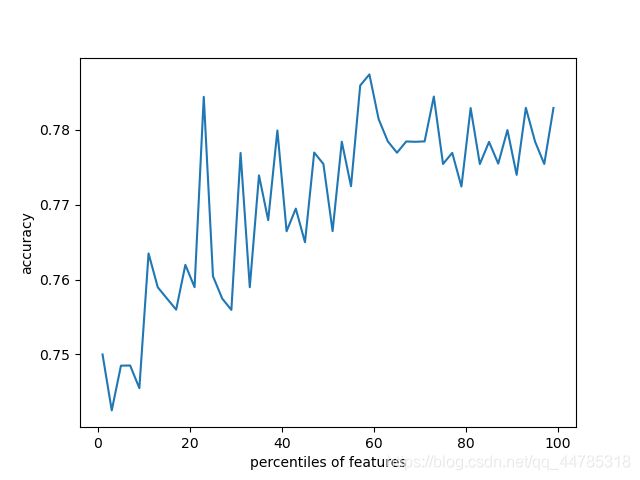
#通过交叉验证的方法，按照固定间隔的百分比筛选特征，并作图展示性能随特征筛选比例的变化
percentiles = range(1,100,2)
results = []

for i in percentiles:
    fs = feature_selection.SelectPercentile(feature_selection.chi2,percentile=i)
    X_train_fs = fs.fit_transform(X_train,y_train)
    #dt为需要使用交叉验证的算法，输入样本，样本标签，cv为交叉验证折数或可迭代的次数
    scores = cross_val_score(dt,X_train_fs,y_train,cv=5)
    #results 为需要被添加的值的数组，scores.mean为添加的值
    results = np.append(results,scores.mean())
print("选择 从前百分之 1到99 间隔为2的特征分别进行预测")
print(results)

pl.plot(percentiles,results)
pl.xlabel("percentiles of features")
pl.ylabel('accuracy')
pl.show()

#使用最佳筛选后的特征，利用相同配置的模型在测试集上进行性能评估
fs = feature_selection.SelectPercentile(feature_selection.chi2,percentile=60)
X_train_fs = fs.fit_transform(X_train,y_train)
dt.fit(X_train_fs,y_train)
X_test_fs = fs.transform(X_test)
print(dt.score(X_test_fs,y_test))

结果：
处理后维度： 684
所有特征进行预测： 0.820627802690583
选择前20%的特征进行预测： 0.8385650224215246
选择 从前百分之 1到99 间隔为2的特征分别进行预测
[0.74998317 0.74250926 0.74849063 0.74851307 0.74548311 0.76349456
 0.75897206 0.7574683  0.75597576 0.76196835 0.75898328 0.78443497
 0.76045337 0.7574683  0.75594209 0.77692739 0.75897206 0.7739311
 0.76794973 0.77993491 0.76645719 0.76948715 0.76498709 0.7769835
 0.7754573  0.76647963 0.77843115 0.77248345 0.78594995 0.78743126
 0.78146112 0.77847604 0.77696106 0.77846482 0.77841993 0.77847604
 0.78446863 0.7754573  0.77693862 0.77243856 0.78293121 0.77544608
 0.77840871 0.77550219 0.77999102 0.77399843 0.78296487 0.7784536
 0.7754573  0.78294243]
0.8116591928251121

进阶篇_第7张图片

 

进阶篇_第8张图片

模型正则化

欠拟合与过拟合

进阶篇_第9张图片

from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pylab as plt

#输入训练样本的特征以及目标值，分别存储在变量 X_train 与 y_train 之中
X_train = [[6],[8],[10],[14],[18]]
y_train = [[7],[9],[13],[17.5],[18]]

#从 sklearn.linear_model 中导入 LinearRegression
#使用默认配置初始化线性回归模型
regressor = LinearRegression()
#直接以披萨的直径作为特征训练模型
regressor.fit(X_train,y_train)
#训练完毕

#导入 numpy 并且重命名为 np
#在 x轴上从0至25均匀采样100个数据点
xx = np.linspace(0,26,100)
xx = xx.reshape(xx.shape[0],1) #改变数组的维数样式
#以上述100个数据点作为基准，预测回归直线
yy = regressor.predict(xx)

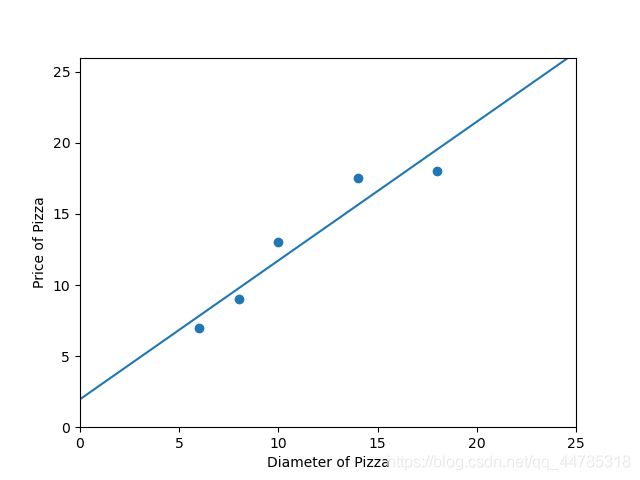
#对回归预测到的直线进行作图
#绘制数据集点
plt.scatter(X_train,y_train)
#在同一张图中画训练完的回归线
plt1, = plt.plot(xx,yy,label ='Degree=1')

plt.axis([0,25,0,26]) #坐标大小为 x、y轴从0到25
plt.xlabel('Diameter of Pizza')
plt.ylabel('Price of Pizza')
plt.legend(handles = [plt1])
plt.show()

#输出线性回归模型在训练样本上的R-squared值
print("The R-squared value of Linear Regressor performing on the training data is",regressor.score(X_train,y_train))

结果：
The R-squared value of Linear Regressor performing on the training data is 0.9100015964240102

进阶篇_第10张图片

进阶篇_第11张图片

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt

#输入训练样本的特征以及目标值，分别存储在变量 X_train 与 y_train 之中
X_train = [[6],[8],[10],[14],[18]]
y_train = [[7],[9],[13],[17.5],[18]]

#以线性回归器为基础，初始化回归模型。尽管特征的维度有提高，但是模型基础仍然是线性模型
regressor_poly2 = LinearRegression()

#从 sklearn.linear_model 中导入 LinearRegression
#使用默认配置初始化线性回归模型
regressor = LinearRegression()

#从 sklearn.preproessing 中导入多项式特征产生器
#使用 PolynorminalFeatures(degress = 2)映射出2次多项式特征，存储在变量 X_train_poly2中
poly2 = PolynomialFeatures(degree=2)
X_train_poly2 = poly2.fit_transform(X_train)


#对2次多项式回归模型进行训练
regressor_poly2.fit(X_train_poly2,y_train)
#直接以披萨的直径作为特征训练模型
regressor.fit(X_train,y_train)

#从新映射绘图用 x 轴采样数据
xx = np.linspace(0,26,100)
xx = xx.reshape(xx.shape[0],1)
xx_poly2 = poly2.transform(xx)

#以上述100个数据点作为基准，预测回归直线
yy = regressor.predict(xx)
#使用2次多项式回归模型对应x轴采样数据进行回归预测
yy_poly2 = regressor_poly2.predict(xx_poly2)

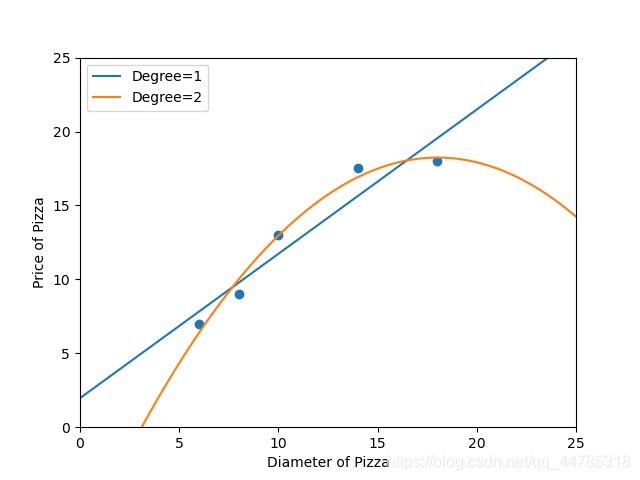
#分别对训练数据点、线型回归直线、2次多项式回归曲线进行作图
plt.scatter(X_train,y_train)

plt1, = plt.plot(xx,yy,label = 'Degree=1')
plt2, = plt.plot(xx,yy_poly2,label = 'Degree=2')

plt.axis([0,25,0,25])
plt.xlabel("Diameter of Pizza")
plt.ylabel("Price of Pizza")
plt.legend(handles = [plt1,plt2])
plt.show()

#输出线性回归模型在训练样本上的R-squared值
print("The R-squared value of Linear Regressor performing on the training data is",regressor.score(X_train,y_train))
#输出2次多项式回归模型在训练样本上的R_squared值
print("The R-squared value of Polynorminak Regressor (Degree=2) performing on the training data is",regressor_poly2.score(X_train_poly2,y_train))

结果：
The R-squared value of Linear Regressor performing on the training data is 0.9100015964240102
The R-squared value of Polynorminak Regressor (Degree=2) performing on the training data is 0.9816421639597427

进阶篇_第12张图片

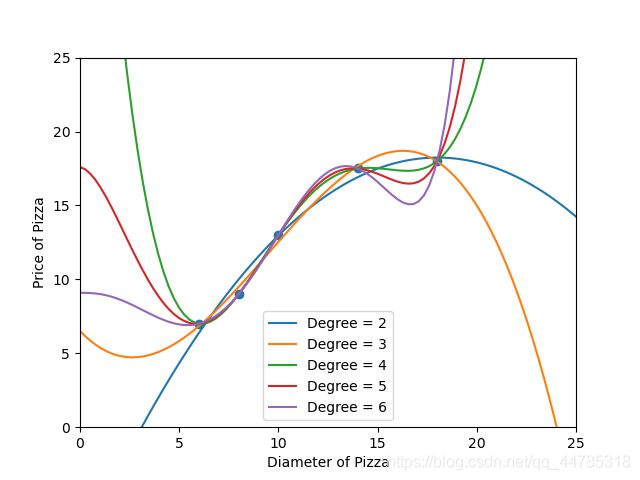
由此进一步升高特征维度

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt

#输入训练样本的特征以及目标值，分别存储在变量 X_train 与 y_train 之中
X_train = [[6],[8],[10],[14],[18]]
y_train = [[7],[9],[13],[17.5],[18]]

#从新映射绘图用 x 轴采样数据
xx = np.linspace(0,26,100)
xx = xx.reshape(xx.shape[0],1)

range = range(2,7)

plt.scatter(X_train,y_train)
plt.axis([0,25,0,25])
plt.xlabel("Diameter of Pizza")
plt.ylabel("Price of Pizza")

pltInfo=[]
for i in range:
    #准备工作
    poly = "poly"+str(i)
    plts = "plt" + str(i)
    Degree = "Degree = "+str(i)
    regressor_poly = "regressor_poly"+str(i)
    xx_poly = "xx_poly" + str(i)
    yy_poly = "yy_poly" + str(i)

    # 从 sklearn.preproessing 中导入多项式特征产生器
    # 使用 PolynorminalFeatures(degress = i)映射出第i次多项式特征，存储在变量 X_train_poly中
    poly = PolynomialFeatures(degree=i)
    X_train_poly = poly.fit_transform(X_train)
    # 以线性回归器为基础，初始化回归模型。尽管特征的维度有提高，但是模型基础仍然是线性模型
    regressor_poly = LinearRegression()
    # 对i次多项式回归模型进行训练
    regressor_poly.fit(X_train_poly,y_train)

    #将xx的数据作为测试集
    xx_poly = poly.transform(xx)
    #训练xx_poly集，并将结果存储到yy_poly
    yy_poly = regressor_poly.predict(xx_poly)

    #将每次作图信息存入一个列表中
    pltInfo.append(plts)
    #定义每一个作图信息
    pltInfo[i-2], =plt.plot(xx,yy_poly,label = Degree)
    #应用作图信息
    plt.legend(handles=pltInfo)
    # 输出i次多项式回归模型在训练样本上的R_squared值
    print("The R-squared value of Polynorminak Regressor (",Degree,") performing on the training data is",regressor_poly.score(X_train_poly, y_train))

plt.show()

结果：
The R-squared value of Polynorminak Regressor ( Degree = 2 ) performing on the training data is 0.9816421639597427
The R-squared value of Polynorminak Regressor ( Degree = 3 ) performing on the training data is 0.9947351016429964
The R-squared value of Polynorminak Regressor ( Degree = 4 ) performing on the training data is 1.0
The R-squared value of Polynorminak Regressor ( Degree = 5 ) performing on the training data is 1.0
The R-squared value of Polynorminak Regressor ( Degree = 6 ) performing on the training data is 1.0

进阶篇_第13张图片

进阶篇_第14张图片

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt

#输入训练样本的特征以及目标值，分别存储在变量 X_train 与 y_train 之中
X_train = [[6],[8],[10],[14],[18]]
y_train = [[7],[9],[13],[17.5],[18]]

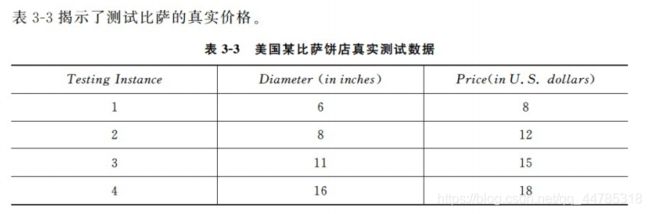
#准备测试数据
X_test = [[6],[8],[11],[16]]
y_test = [[8],[12],[15],[18]]

#使用测试数据对线性回归模型的性能进行评估
regressor = LinearRegression()
regressor.fit(X_train,y_train)
print(regressor.score(X_test,y_test))

#使用测试数据对2次多项式回归模型的性能进行评估
poly2 = PolynomialFeatures(degree=2)
X_train_poly2 = poly2.fit_transform(X_train)

regressor_poly2 = LinearRegression()
regressor_poly2.fit(X_train_poly2,y_train)

X_test_poly2 = poly2.transform(X_test)
print(regressor_poly2.score(X_test_poly2,y_test))

#使用测试数据对4次多项式回归模型的性能进行评估
poly4 = PolynomialFeatures(degree=4)
X_train_poly4 = poly4.fit_transform(X_train)

regressor_poly4 = LinearRegression()
regressor_poly4.fit(X_train_poly4,y_train)

X_test_poly4 = poly4.transform(X_test)
print(regressor_poly4.score(X_test_poly4,y_test))

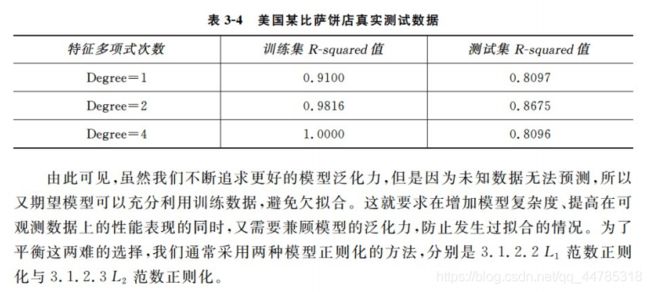
结果：
0.809726797707665
0.8675443656345054
0.8095880795856146

进阶篇_第15张图片

进阶篇_第16张图片

L1范数正则化

进阶篇_第17张图片

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso

#输入训练样本的特征以及目标值，分别存储在变量 X_train 与 y_train 之中
X_train = [[6],[8],[10],[14],[18]]
y_train = [[7],[9],[13],[17.5],[18]]

#准备测试数据
X_test = [[6],[8],[11],[16]]
y_test = [[8],[12],[15],[18]]

#使用测试数据对4次多项式回归模型的性能进行评估
poly4 = PolynomialFeatures(degree=4)
X_train_poly4 = poly4.fit_transform(X_train)

regressor_poly4 = LinearRegression()
regressor_poly4.fit(X_train_poly4,y_train)

X_test_poly4 = poly4.transform(X_test)
print("普通4次多项式",regressor_poly4.score(X_test_poly4,y_test))
#普通4次多项式回归模型的参数列表
print(regressor_poly4.coef_)

#从sklearn.linear_model 中导入Lasso
lasso_poly4 = Lasso()
#从使用 Lasso 对4次多项式特征进行拟合
lasso_poly4.fit(X_train_poly4,y_train)

#对 Lasso模型在测试样本上的回归性能进行评估
print('Lasso模型:',lasso_poly4.score(X_train_poly4,y_train))
print(lasso_poly4.coef_)

结果：
普通4次多项式 0.8095880795856146
[[ 0.00000000e+00 -2.51739583e+01  3.68906250e+00 -2.12760417e-01
   4.29687500e-03]]
Lasso模型: 0.9940832798380284
[ 0.00000000e+00  0.00000000e+00  1.17900534e-01  5.42646770e-05
 -2.23027128e-04]

进阶篇_第18张图片

L2范数正则化

进阶篇_第19张图片

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge

#输入训练样本的特征以及目标值，分别存储在变量 X_train 与 y_train 之中
X_train = [[6],[8],[10],[14],[18]]
y_train = [[7],[9],[13],[17.5],[18]]

#准备测试数据
X_test = [[6],[8],[11],[16]]
y_test = [[8],[12],[15],[18]]

#使用测试数据对4次多项式回归模型的性能进行评估
poly4 = PolynomialFeatures(degree=4)
X_train_poly4 = poly4.fit_transform(X_train)

regressor_poly4 = LinearRegression()
regressor_poly4.fit(X_train_poly4,y_train)

X_test_poly4 = poly4.transform(X_test)
print("普通4次多项式",regressor_poly4.score(X_test_poly4,y_test))
#普通4次多项式回归模型的参数列表
print(regressor_poly4.coef_)
#输出上述这些参数的平方和，验证参数之间的巨大差异
print("普通4次参数平方和：",np.sum(regressor_poly4.coef_ ** 2))
print("---"*20)
#从 sklearn.linear_model 导入 Ridge
ridge_poly4 = Ridge()
#使用 Ridge 模型对4次多项式特征进行拟合
ridge_poly4.fit(X_train_poly4,y_train)
#输出Ridge模型在测试样本上的回归性能
print(ridge_poly4.score(X_test_poly4,y_test))
#输出 Ridge 模型的参数列表，观察参数差异
print(ridge_poly4.coef_)
#计算 Ridge 模型拟合后参数的平方和
print("Ridge 模型平方和：",np.sum(ridge_poly4.coef_ ** 2))
print("---"*20)
#从sklearn.linear_model 中导入Lasso
lasso_poly4 = Lasso()
#从使用 Lasso 对4次多项式特征进行拟合
lasso_poly4.fit(X_train_poly4,y_train)
#对 Lasso模型在测试样本上的回归性能进行评估
print('Lasso模型:',lasso_poly4.score(X_train_poly4,y_train))
print('Lasso模型平方和:',np.sum(lasso_poly4.coef_ ** 2))

结果：
普通4次多项式 0.8095880795856146
[[ 0.00000000e+00 -2.51739583e+01  3.68906250e+00 -2.12760417e-01
   4.29687500e-03]]
普通4次参数平方和： 647.3826456916975
------------------------------------------------------------
0.8374201759366509
[[ 0.         -0.00492536  0.12439632 -0.00046471 -0.00021205]]
Ridge 模型平方和： 0.015498965203562037
------------------------------------------------------------
Lasso模型: 0.9940832798380284
Lasso模型平方和: 0.01390058867089999

进阶篇_第20张图片

模型检测

进阶篇_第21张图片

留一验证

进阶篇_第22张图片

交叉验证

进阶篇_第23张图片

超参数搜索

进阶篇_第24张图片

网格搜索

进阶篇_第25张图片

from sklearn.datasets import fetch_20newsgroups
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.pipeline import Pipeline
from  sklearn.model_selection import GridSearchCV

#从sklearn,datasets 中导入20类新闻文本抓取器
#导入 numpy,并且重命名为np

#使用新闻抓取器从互联网上下载所有数据，并且存储在变量news中
news = fetch_20newsgroups(subset="all")
#sklearn.model_selection 导入 train_test_split 用来分割数据
#对前 3000 条新闻文本进行数据分割，25%文本用于未来测试
X_train,X_test,y_train,y_test = train_test_split(news.data[:3000],news.target[:3000],test_size=0.25,random_state=33)

#导入支持向量机(分类)模型
#导入 TfidfVectorizer 文本抽取器
#导入 Pipeline

#使用 Pipeline 简化系统搭建流程，将文本抽取与分类器模型串联起来
clf = Pipeline([('vect',TfidfVectorizer(stop_words='english',analyzer='word')),('svc',SVC())])

#这里需要实验的2个超参数的个数分别是 4、3，svc_gamma的参数共用10^-2，10^--1...这样我们一共有12中的超参数组合，12个不同参数下的模型
parameters = {'svc__gamma':np.logspace(-2,1,4),'svc__C':np.logspace(-1,1,3)}

#从 sklearn.model_selection 中导入网格搜索模块 GridSearchCV
#将12组参数组合以及初始化的Pipline包括 3折交叉验证的要求全部告知 GridSearchCV。请大家务必注意 refit=True 这样一个设定
gs = GridSearchCV(clf,parameters,verbose=2,refit=True,cv = 3)

#执行单线程网格搜索
gs.fit(X_train,y_train)
print(gs.best_params_,gs.best_score_)

#输出最佳模型在测试集上的准确性
print(gs.score(X_test,y_test))

结果：
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
Fitting 3 folds for each of 12 candidates, totalling 36 fits
[CV] svc__C=0.1, svc__gamma=0.01 .....................................
[CV] ...................... svc__C=0.1, svc__gamma=0.01, total=   4.2s
[CV] svc__C=0.1, svc__gamma=0.01 .....................................
[Parallel(n_jobs=1)]: Done   1 out of   1 | elapsed:    4.1s remaining:    0.0s
[CV] ...................... svc__C=0.1, svc__gamma=0.01, total=   4.2s
[CV] svc__C=0.1, svc__gamma=0.01 .....................................
[CV] ...................... svc__C=0.1, svc__gamma=0.01, total=   4.2s
[CV] svc__C=0.1, svc__gamma=0.1 ......................................
[CV] ....................... svc__C=0.1, svc__gamma=0.1, total=   4.2s
[CV] svc__C=0.1, svc__gamma=0.1 ......................................
[CV] ....................... svc__C=0.1, svc__gamma=0.1, total=   4.2s
[CV] svc__C=0.1, svc__gamma=0.1 ......................................
[CV] ....................... svc__C=0.1, svc__gamma=0.1, total=   4.2s
[CV] svc__C=0.1, svc__gamma=1.0 ......................................
[CV] ....................... svc__C=0.1, svc__gamma=1.0, total=   4.2s
[CV] svc__C=0.1, svc__gamma=1.0 ......................................
[CV] ....................... svc__C=0.1, svc__gamma=1.0, total=   4.3s
[CV] svc__C=0.1, svc__gamma=1.0 ......................................
[CV] ....................... svc__C=0.1, svc__gamma=1.0, total=   4.3s
[CV] svc__C=0.1, svc__gamma=10.0 .....................................
[CV] ...................... svc__C=0.1, svc__gamma=10.0, total=   4.2s
[CV] svc__C=0.1, svc__gamma=10.0 .....................................
[CV] ...................... svc__C=0.1, svc__gamma=10.0, total=   4.3s
[CV] svc__C=0.1, svc__gamma=10.0 .....................................
[CV] ...................... svc__C=0.1, svc__gamma=10.0, total=   4.3s
[CV] svc__C=1.0, svc__gamma=0.01 .....................................
[CV] ...................... svc__C=1.0, svc__gamma=0.01, total=   4.2s
[CV] svc__C=1.0, svc__gamma=0.01 .....................................
[CV] ...................... svc__C=1.0, svc__gamma=0.01, total=   4.2s
[CV] svc__C=1.0, svc__gamma=0.01 .....................................
[CV] ...................... svc__C=1.0, svc__gamma=0.01, total=   4.2s
[CV] svc__C=1.0, svc__gamma=0.1 ......................................
[CV] ....................... svc__C=1.0, svc__gamma=0.1, total=   4.2s
[CV] svc__C=1.0, svc__gamma=0.1 ......................................
[CV] ....................... svc__C=1.0, svc__gamma=0.1, total=   4.2s
[CV] svc__C=1.0, svc__gamma=0.1 ......................................
[CV] ....................... svc__C=1.0, svc__gamma=0.1, total=   4.2s
[CV] svc__C=1.0, svc__gamma=1.0 ......................................
[CV] ....................... svc__C=1.0, svc__gamma=1.0, total=   4.3s
[CV] svc__C=1.0, svc__gamma=1.0 ......................................
[CV] ....................... svc__C=1.0, svc__gamma=1.0, total=   4.3s
[CV] svc__C=1.0, svc__gamma=1.0 ......................................
[CV] ....................... svc__C=1.0, svc__gamma=1.0, total=   4.3s
[CV] svc__C=1.0, svc__gamma=10.0 .....................................
[CV] ...................... svc__C=1.0, svc__gamma=10.0, total=   4.3s
[CV] svc__C=1.0, svc__gamma=10.0 .....................................
[CV] ...................... svc__C=1.0, svc__gamma=10.0, total=   4.3s
[CV] svc__C=1.0, svc__gamma=10.0 .....................................
[CV] ...................... svc__C=1.0, svc__gamma=10.0, total=   4.4s
[CV] svc__C=10.0, svc__gamma=0.01 ....................................
[CV] ..................... svc__C=10.0, svc__gamma=0.01, total=   4.1s
[CV] svc__C=10.0, svc__gamma=0.01 ....................................
[CV] ..................... svc__C=10.0, svc__gamma=0.01, total=   4.2s
[CV] svc__C=10.0, svc__gamma=0.01 ....................................
[CV] ..................... svc__C=10.0, svc__gamma=0.01, total=   4.2s
[CV] svc__C=10.0, svc__gamma=0.1 .....................................
[CV] ...................... svc__C=10.0, svc__gamma=0.1, total=   4.2s
[CV] svc__C=10.0, svc__gamma=0.1 .....................................
[CV] ...................... svc__C=10.0, svc__gamma=0.1, total=   4.2s
[CV] svc__C=10.0, svc__gamma=0.1 .....................................
[CV] ...................... svc__C=10.0, svc__gamma=0.1, total=   4.3s
[CV] svc__C=10.0, svc__gamma=1.0 .....................................
[CV] ...................... svc__C=10.0, svc__gamma=1.0, total=   4.3s
[CV] svc__C=10.0, svc__gamma=1.0 .....................................
[CV] ...................... svc__C=10.0, svc__gamma=1.0, total=   4.3s
[CV] svc__C=10.0, svc__gamma=1.0 .....................................
[CV] ...................... svc__C=10.0, svc__gamma=1.0, total=   4.3s
[CV] svc__C=10.0, svc__gamma=10.0 ....................................
[CV] ..................... svc__C=10.0, svc__gamma=10.0, total=   4.3s
[CV] svc__C=10.0, svc__gamma=10.0 ....................................
[CV] ..................... svc__C=10.0, svc__gamma=10.0, total=   4.4s
[CV] svc__C=10.0, svc__gamma=10.0 ....................................
[CV] ..................... svc__C=10.0, svc__gamma=10.0, total=   4.4s
[Parallel(n_jobs=1)]: Done  36 out of  36 | elapsed:  2.6min finished
{'svc__C': 10.0, 'svc__gamma': 0.1} 0.7888888888888889
0.8226666666666667

并行搜索

进阶篇_第26张图片

from sklearn.datasets import fetch_20newsgroups
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.pipeline import Pipeline
from  sklearn.model_selection import GridSearchCV

#从sklearn,datasets 中导入20类新闻文本抓取器
#导入 numpy,并且重命名为np

#使用新闻抓取器从互联网上下载所有数据，并且存储在变量news中
news = fetch_20newsgroups(subset="all")
#sklearn.model_selection 导入 train_test_split 用来分割数据
#对前 3000 条新闻文本进行数据分割，25%文本用于未来测试
X_train,X_test,y_train,y_test = train_test_split(news.data[:3000],news.target[:3000],test_size=0.25,random_state=33)

#导入支持向量机(分类)模型
#导入 TfidfVectorizer 文本抽取器
#导入 Pipeline

#使用 Pipeline 简化系统搭建流程，将文本抽取与分类器模型串联起来
clf = Pipeline([('vect',TfidfVectorizer(stop_words='english',analyzer='word')),('svc',SVC())])

#这里需要实验的2个超参数的个数分别是 4、3，svc_gamma的参数共用10^-2，10^--1...这样我们一共有12中的超参数组合，12个不同参数下的模型
#logspace为生成等比数列 默认底数为10（-2，1，4）指从幂-2 -1 0 1 共4个
parameters = {'svc__gamma':np.logspace(-2,1,4),'svc__C':np.logspace(-1,1,3)}

#从 sklearn.model_selection 中导入网格搜索模块 GridSearchCV
#将12组参数组合以及初始化的Pipline包括 3折交叉验证的要求全部告知 GridSearchCV。请大家务必注意 refit=True 这样一个设定
#初始化配置并行网格搜索,n_jobs = -1代表使用该计算机全部的CPU
gs = GridSearchCV(clf,parameters,verbose=2,refit=True,cv = 3,n_jobs=-1)

#执行多线程并行网格搜索
gs.fit(X_train,y_train)
print(gs.best_params_,gs.best_score_)

#输出最佳模型在测试集上的准确性
print(gs.score(X_test,y_test))

结果：
D:\anaconda3\envs\pythonProject1\python.exe D:/PycharmProjects/test1/1.py
Fitting 3 folds for each of 12 candidates, totalling 36 fits
[Parallel(n_jobs=-1)]: Using backend LokyBackend with 12 concurrent workers.
[CV] svc__C=0.1, svc__gamma=0.01 .....................................
[CV] svc__C=0.1, svc__gamma=0.01 .....................................
[CV] svc__C=0.1, svc__gamma=0.01 .....................................
[CV] svc__C=0.1, svc__gamma=0.1 ......................................
[CV] svc__C=0.1, svc__gamma=0.1 ......................................
[CV] svc__C=0.1, svc__gamma=0.1 ......................................
[CV] svc__C=0.1, svc__gamma=1.0 ......................................
[CV] svc__C=0.1, svc__gamma=10.0 .....................................
[CV] svc__C=0.1, svc__gamma=10.0 .....................................
[CV] svc__C=0.1, svc__gamma=1.0 ......................................
[CV] svc__C=0.1, svc__gamma=1.0 ......................................
[CV] svc__C=0.1, svc__gamma=10.0 .....................................
[CV] ...................... svc__C=0.1, svc__gamma=0.01, total=   5.9s
[CV] ...................... svc__C=0.1, svc__gamma=0.01, total=   5.9s
[CV] svc__C=1.0, svc__gamma=0.01 .....................................
[CV] svc__C=1.0, svc__gamma=0.01 .....................................
[CV] ....................... svc__C=0.1, svc__gamma=0.1, total=   5.9s
[CV] ...................... svc__C=0.1, svc__gamma=0.01, total=   6.0s
[CV] ....................... svc__C=0.1, svc__gamma=0.1, total=   5.9s
[CV] svc__C=1.0, svc__gamma=0.01 .....................................
[CV] svc__C=1.0, svc__gamma=0.1 ......................................
[CV] svc__C=1.0, svc__gamma=0.1 ......................................
[CV] ....................... svc__C=0.1, svc__gamma=0.1, total=   6.0s
[CV] ....................... svc__C=0.1, svc__gamma=1.0, total=   6.0s
[CV] svc__C=1.0, svc__gamma=0.1 ......................................
[CV] svc__C=1.0, svc__gamma=1.0 ......................................
[CV] ...................... svc__C=0.1, svc__gamma=10.0, total=   6.0s
[CV] svc__C=1.0, svc__gamma=1.0 ......................................
[CV] ...................... svc__C=0.1, svc__gamma=10.0, total=   7.7s
[CV] svc__C=1.0, svc__gamma=1.0 ......................................
[CV] ...................... svc__C=0.1, svc__gamma=10.0, total=   7.8s
[CV] svc__C=1.0, svc__gamma=10.0 .....................................
[CV] ....................... svc__C=0.1, svc__gamma=1.0, total=   8.1s
[CV] svc__C=1.0, svc__gamma=10.0 .....................................
[CV] ....................... svc__C=0.1, svc__gamma=1.0, total=   8.9s
[CV] svc__C=1.0, svc__gamma=10.0 .....................................
[CV] ...................... svc__C=1.0, svc__gamma=0.01, total=   5.9s
[CV] svc__C=10.0, svc__gamma=0.01 ....................................
[CV] ....................... svc__C=1.0, svc__gamma=0.1, total=   6.3s
[CV] svc__C=10.0, svc__gamma=0.01 ....................................
[CV] ....................... svc__C=1.0, svc__gamma=1.0, total=   6.3s
[CV] svc__C=10.0, svc__gamma=0.01 ....................................
[CV] ....................... svc__C=1.0, svc__gamma=1.0, total=   6.4s
[CV] svc__C=10.0, svc__gamma=0.1 .....................................
[CV] ...................... svc__C=1.0, svc__gamma=0.01, total=   7.5s
[CV] svc__C=10.0, svc__gamma=0.1 .....................................
[CV] ....................... svc__C=1.0, svc__gamma=0.1, total=   7.6s
[CV] ...................... svc__C=1.0, svc__gamma=0.01, total=   7.7s
[CV] ....................... svc__C=1.0, svc__gamma=0.1, total=   7.5s
[CV] svc__C=10.0, svc__gamma=0.1 .....................................
[CV] svc__C=10.0, svc__gamma=1.0 .....................................
[CV] svc__C=10.0, svc__gamma=1.0 .....................................
[CV] ...................... svc__C=1.0, svc__gamma=10.0, total=   6.0s
[CV] svc__C=10.0, svc__gamma=1.0 .....................................
[CV] ....................... svc__C=1.0, svc__gamma=1.0, total=   6.7s
[CV] svc__C=10.0, svc__gamma=10.0 ....................................
[CV] ...................... svc__C=1.0, svc__gamma=10.0, total=   7.6s
[CV] svc__C=10.0, svc__gamma=10.0 ....................................
[CV] ...................... svc__C=1.0, svc__gamma=10.0, total=   7.3s
[CV] svc__C=10.0, svc__gamma=10.0 ....................................
[CV] ..................... svc__C=10.0, svc__gamma=0.01, total=   6.4s
[CV] ..................... svc__C=10.0, svc__gamma=0.01, total=   6.0s
[CV] ..................... svc__C=10.0, svc__gamma=0.01, total=   6.4s
[CV] ...................... svc__C=10.0, svc__gamma=0.1, total=   6.4s
[CV] ...................... svc__C=10.0, svc__gamma=1.0, total=   6.0s
[CV] ...................... svc__C=10.0, svc__gamma=0.1, total=   6.9s
[CV] ...................... svc__C=10.0, svc__gamma=1.0, total=   6.8s
[Parallel(n_jobs=-1)]: Done  32 out of  36 | elapsed:   22.9s remaining:    2.8s
[CV] ...................... svc__C=10.0, svc__gamma=0.1, total=   6.9s
[CV] ...................... svc__C=10.0, svc__gamma=1.0, total=   6.9s
[CV] ..................... svc__C=10.0, svc__gamma=10.0, total=   5.9s
[CV] ..................... svc__C=10.0, svc__gamma=10.0, total=   5.7s
[CV] ..................... svc__C=10.0, svc__gamma=10.0, total=   5.5s
[Parallel(n_jobs=-1)]: Done  36 out of  36 | elapsed:   24.4s finished
{'svc__C': 10.0, 'svc__gamma': 0.1} 0.7888888888888889
0.8226666666666667

流行库/模型实践

进阶篇_第27张图片

自然语言处理包（NLTK）

进阶篇_第28张图片

from sklearn.feature_extraction.text import CountVectorizer

#将上述两个句子以字符串的数据类型分别存储在变量 sent1 与 sent2中
sent1 = "The cat is walking in the bedroom."
sent2 = "A dog was running access the kitchen."

#从 sklearn.feature_extraction.text 中导入 CountVectorizer
count_vec = CountVectorizer()

sentences = [sent1,sent2]

#输出特征向量化后的表示
print(count_vec.fit_transform(sentences).toarray())
#输出向量各个维度的特征含义
print(count_vec.get_feature_names())

结果：
[[0 1 1 0 1 1 0 0 2 1 0]
 [1 0 0 1 0 0 1 1 1 0 1]]
['access', 'bedroom', 'cat', 'dog', 'in', 'is', 'kitchen', 'running', 'the', 'walking', 'was']


from sklearn.feature_extraction.text import CountVectorizer
import nltk

#将上述两个句子以字符串的数据类型分别存储在变量 sent1 与 sent2中
sent1 = "The cat is walking in the bedroom."
sent2 = "A dog was running access the kitchen."
sentences = [sent1,sent2]

#从 sklearn.feature_extraction.text 中导入 CountVectorizer
count_vec = CountVectorizer()
#输出特征向量化后的表示
print(count_vec.fit_transform(sentences).toarray())
#输出向量各个维度的特征含义
print(count_vec.get_feature_names())
print("--"*40)

#导入 nltk
#对句子进行词汇分割和正规化，有些情况如aren't 需要分割为 are 和 n't ;或者 I'm要分割为I和'm
tokens_1 = nltk.word_tokenize(sent1)
print(tokens_1)
tokens_2 = nltk.word_tokenize(sent2)
print(tokens_2)
print("--"*40)

#整理两句的词表，并且按照ASCLL的排序输出
#set为去重
vocab_1 = sorted(set(tokens_1))
print(vocab_1)
vocab_2 = sorted(set(tokens_2))
print(vocab_2)
print("--"*40)

#初始化 stemmer 寻找各个词汇最原始的词根
stemmer = nltk.stem.PorterStemmer()
stem_1 = [stemmer.stem(t) for t in tokens_1]
print(stem_1)
stem_2 = [stemmer.stem(t) for t in tokens_2]
print(stem_2)
print("--"*40)

#初始化词性标注器，对每个词汇进行标注
pos_tag_1 = nltk.tag.pos_tag(tokens_1)
print(pos_tag_1)
pos_tag_2 = nltk.tag.pos_tag(tokens_2)
print(pos_tag_2)

结果：
[[0 1 1 0 1 1 0 0 2 1 0]
 [1 0 0 1 0 0 1 1 1 0 1]]
['access', 'bedroom', 'cat', 'dog', 'in', 'is', 'kitchen', 'running', 'the', 'walking', 'was']
--------------------------------------------------------------------------------
['The', 'cat', 'is', 'walking', 'in', 'the', 'bedroom', '.']
['A', 'dog', 'was', 'running', 'access', 'the', 'kitchen', '.']
--------------------------------------------------------------------------------
['.', 'The', 'bedroom', 'cat', 'in', 'is', 'the', 'walking']
['.', 'A', 'access', 'dog', 'kitchen', 'running', 'the', 'was']
--------------------------------------------------------------------------------
['the', 'cat', 'is', 'walk', 'in', 'the', 'bedroom', '.']
['A', 'dog', 'wa', 'run', 'access', 'the', 'kitchen', '.']
--------------------------------------------------------------------------------
[('The', 'DT'), ('cat', 'NN'), ('is', 'VBZ'), ('walking', 'VBG'), ('in', 'IN'), ('the', 'DT'), ('bedroom', 'NN'), ('.', '.')]
[('A', 'DT'), ('dog', 'NN'), ('was', 'VBD'), ('running', 'VBG'), ('access', 'NN'), ('the', 'DT'), ('kitchen', 'NN'), ('.', '.')]

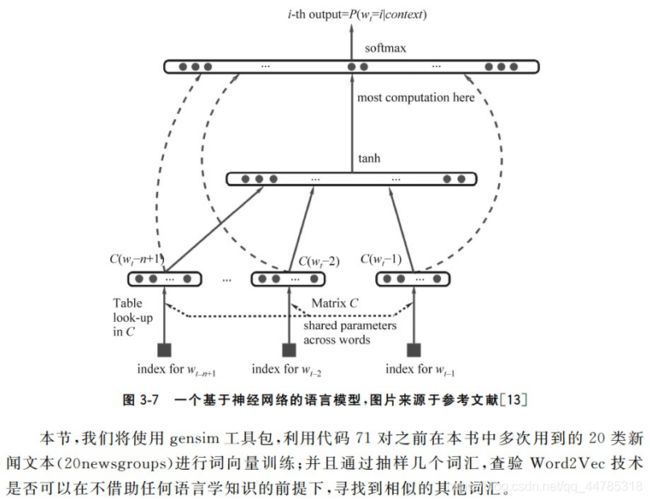
词向量(Word2Vec)技术

进阶篇_第29张图片

进阶篇_第30张图片

from sklearn.datasets import fetch_20newsgroups
from bs4 import BeautifulSoup
import nltk, re
from gensim.models import word2vec

#定义一个函数名为news_to_sentences将每条新闻中的句子逐一剥离出来，
#并返回一个句子逐一剥离出来，并返回一个句子列表。
def news_to_sentences(news):
    news_text = BeautifulSoup(news).get_text()
    tokenizer = nltk.data.load('tokenizers/punkt/english.pickle')
    raw_sentences = tokenizer.tokenize(news_text)
    sentences = []
    for sent in raw_sentences:
        sentences.append(re.sub('[^a-zA-Z]', ' ', sent.lower().strip()).split())
    return sentences


news = fetch_20newsgroups(subset='all')
X, y = news.data, news.target

sentences = []
#将长篇新闻文本中的句子剥离出来，用于训练。
for x in X:
    sentences += news_to_sentences(x)

#配置词向量的维度。
num_features = 300
#保证被考虑的词汇的频度
min_word_count = 20
#设定并行化训练使用CPU计算核心的数量，多核可用。
num_workers = 2
#定义训练词向量的上下文窗口大小
context = 5
downsampling = 1e-3

model = word2vec.Word2Vec(sentences, workers=num_workers,\
                          size=num_features, min_count=min_word_count,\
                          window=context, sample=downsampling)
#这个设定代表当前训练好的词向量为最终版，也可以加快模型的训练速度。
model.init_sims(replace=True)
#利用训练好的模型，寻找训练文本中与morning最相关的10个词汇
print(model.most_similar('morning'))
#利用训练好的模型，寻找训练文本中与email最相关的10个词汇。
print(model.most_similar('email'))

结果：
[('afternoon', 0.8125509023666382), ('weekend', 0.7887392044067383), ('evening', 0.7872912883758545), ('night', 0.7082017064094543), ('saturday', 0.6989781260490417), ('friday', 0.6907871961593628), ('sunday', 0.6815508604049683), ('newspaper', 0.6693010926246643), ('week', 0.6428839564323425), ('summer', 0.6331900358200073)]
[('mail', 0.7351820468902588), ('contact', 0.6784430742263794), ('request', 0.660675048828125), ('address', 0.6446553468704224), ('send', 0.62925785779953), ('subscription', 0.627805769443512), ('listserv', 0.6215932369232178), ('snail', 0.6207793951034546), ('mailed', 0.6121481657028198), ('replies', 0.6098143458366394)]

进阶篇_第31张图片

XGBoost模型

进阶篇_第32张图片

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction import DictVectorizer
from sklearn.ensemble import  RandomForestClassifier
from xgboost import XGBClassifier

#导入 pandas 用于数据分析

#通过 URL 地址来下载Titanic 数据
#titanic = pd.read_csv('http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt')
titanic = pd.read_csv('train.csv')

#选取 pclass、age 以及sex作为训练特征
X = titanic[['Pclass','Age','Sex']]
y = titanic['Survived']

#对缺失的age 信息，采用平均值方法进行补全，即以age列已知数据的平均数填充
X['Age'].fillna(X['Age'].mean(),inplace=True)

#对原数据进行分割，随机采样25%作为测试集
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.25,random_state=33)
#从 sklearn.feature)extraction 导入 Dictvectorizer
vec = DictVectorizer(sparse=False)

#对原数据进行特征向量化处理
X_train = vec.fit_transform(X_train.to_dict(orient = 'records'))
X_test = vec.transform(X_test.to_dict(orient = 'records'))

#采用默认配置的随机森林分类器对测试集进行预测
rfc = RandomForestClassifier()
rfc.fit(X_train,y_train)
print("The accuracy if Random Forest Classifier on testing set:",rfc.score(X_test,y_test))

#采用默认配置的 XFGBoost 模型对相同的测试集进行预测
xgbc = XGBClassifier()
xgbc.fit(X_train,y_train)
print("The accuracy of eXtrem Gradient Boosting Classifier on testing set:",xgbc.score(X_test,y_test))

结果:
accuracy if Random Forest Classifier on testing set: 0.8295964125560538
The accuracy of eXtrem Gradient Boosting Classifier on testing set: 0.8385650224215246

进阶篇_第33张图片

Tensorflow框架

使用 Tensorflow 输出一句话

import tensorflow as tf
import numpy as np

#导入 tensorflow 工具包并重命名为tf
#导入 numpy 并重命名为np

#初始化一个 Tensorflow 的常量：Hello Google Tensorflow! 字符串,并命名为 greeting 作为一个计算模块
greeting = tf.constant("Hello Google Tensorflow!")

#启动一个会话
sess = tf.Session()
#使用会话执行 greeting 计算模块
result = sess.run(greeting)
#输出会话执行的结果
print(result)
#关闭会话，这是一种显示关闭会话的方式
sess.close()

结果：
b'Hello Google Tensorflow!'

使用 Tensorflow 完成一次线性函数的计算

import tensorflow as tf

#导入 tensorflow 工具包并重命名为tf

#启动一个会话
sess = tf.Session()

#声明 matrix1 为 Tensorflow 的一个 1*2 的行向量
matrix1 = tf.constant([[3.,3.]])
#声明 matrix2 为 Tensorflow 的一个 2*1 的列向量
matrix2 = tf.constant([[2.],[2.]])

#product 将上述两个算子相乘，作为新算例
product = tf.matmul(matrix1,matrix2) #结果：12
#继续将 product 与一个标量 2.0 求和拼接，作为最终的linear 算例
linear = tf.add(product,tf.constant(2.0))

#直接在会话中执行 linear 算例，相当于将上面所有的单独算例拼接成流程图来执行
with tf.Session() as sess:
    result = sess.run(linear)
    print(result)

结果：
[[14.]]

进阶篇_第34张图片

import tensorflow as tf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


#导入 tensorflow 工具包并重命名为tf
#导入 numpy
#导入 pandas

#从本地使用 pandas 读取乳腺癌肿瘤的训练和测试数据
#https://note.youdao.com/coshare/index.html?token=C6B145FA919F41F8ACAAC39EE775441C&gid=93772390
train = pd.read_csv('breast-cancer-train.csv')
test = pd.read_csv('breast-cancer-test.csv')
#分割特征与分类目标
X_train = np.float32(train[['Clump Thickness','Cell Size']].T)
y_train = np.float32(train['Type'].T)
X_test = np.float32(test[['Clump Thickness','Cell Size']].T)
y_test = np.float32(test['Type'].T)

#定义一个 tensorflow 的变量b作为线性模型的截距，同时设置初始值为1.0
b = tf.Variable(tf.zeros([1]))
#定义一个tensorflow 的变量W作为线性模型的系数，并设置初始值为-1.0至1.0之间均匀分布的随机数
W = tf.Variable(tf.random_uniform([1,2],-1.0,1.0))
#显示定义这个线性函数
y = tf.matmul(W,X_train) + b

#使用tensorflow 中的reduce_mean取得训练集上均方误差
loss = tf.reduce_mean(tf.square(y-y_train))

#使用梯度下降法估计参数 W,b,并且设置迭代步长为0.01，这个与Scikit-learn中的SEGRegressor类似
optimizer= tf.train.GradientDescentOptimizer(0.01)

#以最小二乘损失为优化目标
train = optimizer.minimize(loss)

#初始化所有变量
init = tf.global_variables_initializer()

#开启 Tensorflow 中的会话
sess = tf.Session()

#执行变量初始化操作
sess.run(init)

#迭代 2000 轮次 ，训练参数
for step in range(1,2001):
    sess.run(train)
    if step%200==0:
        print(step,sess.run(W),sess.run(b))

#准备测试样本
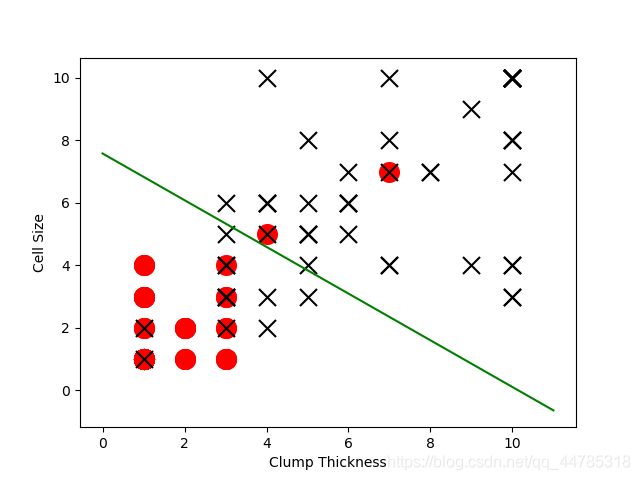
test_negative = test.loc[test['Type'] == 0][['Clump Thickness','Cell Size']]
test_positive = test.loc[test['Type'] == 1][['Clump Thickness','Cell Size']]

#以最终更新的参数作图
plt.scatter(test_negative['Clump Thickness'],test_negative['Cell Size'],marker='o',s=200,c='red')
plt.scatter(test_positive['Clump Thickness'],test_positive['Cell Size'],marker='x',s=150,c='black')
plt.xlabel('Clump Thickness')
plt.ylabel("Cell Size")

#取0-11个数当x值
lx = np.arange(0,12)
#计算12个X对应的y值
#这里要强调一下，我们以0.5作为分界面，所有计算方式如下,0.5-b-wx
ly = (0.5 - sess.run(b) - lx * sess.run(W)[0][0]) / sess.run(W)[0][1]
print(sess.run(b))
print(sess.run(W))
plt.plot(lx,ly,color = 'green')
plt.show()


结果：
200 [[0.01551242 0.12061065]] [-0.09584526]
400 [[0.05568662 0.08001342]] [-0.08955325]
600 [[0.05773812 0.07763022]] [-0.08739269]
800 [[0.05785108 0.07744841]] [-0.08697367]
1000 [[0.05785864 0.07742859]] [-0.08690023]
1200 [[0.05785936 0.07742577]] [-0.08688771]
1400 [[0.05785941 0.07742535]] [-0.08688553]
1600 [[0.05785941 0.07742535]] [-0.08688553]
1800 [[0.05785941 0.07742535]] [-0.08688553]
2000 [[0.05785941 0.07742535]] [-0.08688553]
[-0.08688553]
[[0.05785941 0.07742535]]

进阶篇_第35张图片

进阶篇_第36张图片

进阶篇_第37张图片

进阶篇_第38张图片

进阶篇_第39张图片

进阶篇_第40张图片

 

你可能感兴趣的:(⑉་,机器学习及实践（书）,་⑉,机器学习,深度学习,python,数据挖掘)

  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • 谢谢你们，爱你们！ 鹿游儿
    昨天家人去泡温泉，二个孩子也带着去，出发前一晚，匆匆下班，赶回家和孩子一起收拾。饭后，我拿出笔和本子（上次去澳门时做手帐的本子）写下了1\2\3\4\5\6\7\8\9,让后让小壹去思考，带什么出发去旅游呢？她在对应的数字旁边画上了，泳衣、泳圈、肖恩、内衣内裤、tapuy、拖鞋……画完后，就让她自己对着这个本子，将要带的，一一带上，没想到这次带的书还是这本《便便工厂》(晚上姑婆发照片过来，妹妹累得
  • 理解Gunicorn：Python WSGI服务器的基石 范范0825 ipythonlinux运维
    理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
  • 小丽成长记（四十三） 玲玲54321
    小丽发现，即使她好不容易调整好自己的心态下一秒总会有不确定的伤脑筋的事出现，一个接一个的问题，人生就没有停下的时候，小问题不断出现。不过她今天看的书，她接受了人生就是不确定的，厉害的人就是不断创造确定性，在Ta的领域比别人多的确定性就能让自己脱颖而出，显示价值从而获得的比别人多的利益。正是这样的原因，因为从前修炼自己太少，使得她现在在人生道路上打怪起来困难重重，她似乎永远摆脱不了那种无力感，有种习
  • 我校举行新老教师师徒结对仪式暨名师专业工作室工作交流活动 李蕾1229
    为促进我校教师专业发展，发挥骨干教师的引领带头作用，11月6日下午，我校举行新老教师师徒结对仪式暨名师专业工作室工作交流活动。图片发自App会议由教师发展处李蕾主任主持，首先，由范校长宣读新老教师结对名单及双方承担职责。随后，两位新调入教师陈玉萍、莫正杰分别和他们的师傅鲍元美、刘召彬老师签订了师徒结对协议书。图片发自App图片发自App师徒拥抱、握手。有了师傅就有了目标有了方向，相信两位新教师在师
  • 向内而求 陈陈_19b4
    10月27日，阴。阅读书目:《次第花开》。作者:希阿荣博堪布，是当今藏传佛家宁玛派最伟大的上师法王，如意宝晋美彭措仁波切颇具影响力的弟子之一。多年以来，赴海内外各地弘扬佛法，以正式授课、现场开示、发表文章等多种方法指导佛学弟子修行佛法。代表作《寂静之道》、《生命这出戏》、《透过佛法看世界》自出版以来一直是佛教类书籍中的畅销书。图片发自App金句:1.佛陀说，一切痛苦的根源在于我们长期以来对自身及外
  • Python数据分析与可视化实战指南 William数据分析 pythonpython数据
    在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
  • python os.environ 江湖偌大 python深度学习
    os.environ['TF_CPP_MIN_LOG_LEVEL']='0'#默认值，输出所有信息os.environ['TF_CPP_MIN_LOG_LEVEL']='1'#屏蔽通知信息（INFO）os.environ['TF_CPP_MIN_LOG_LEVEL']='2'#屏蔽通知信息和警告信息（INFO\WARNING）os.environ['TF_CPP_MIN_LOG_LEVEL']='
  • Python中os.environ基本介绍及使用方法 鹤冲天Pro #Pythonpython服务器开发语言
    文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
  • Pyecharts数据可视化大屏：打造沉浸式数据分析体验 我的运维人生 信息可视化数据分析数据挖掘运维开发技术共享
    Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
  • Python教程：一文了解使用Python处理XPath 旦莫 Python进阶python开发语言
    目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
  • python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 pythonos.environ
    >>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
  • 将cmd中命令输出保存为txt文本文件 落难Coder Windowscmdwindow
    最近深度学习本地的训练中我们常常要在命令行中运行自己的代码，无可厚非，我们有必要保存我们的炼丹结果，但是复制命令行输出到txt是非常麻烦的，其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是：运行指令>输出到的文件名称或者具体保存路径测试下，我打开cmd并且ping一下百度：pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出：如果你再
  • 感赏日志133 马姐读书
    图片发自App感赏自己今天买个扫地机，以后可以解放出来多看点书，让这个智能小机器人替我工作了。感赏孩子最近进步很大，每天按时上学，认真听课，认真背书，主动认真完成老师布置的作业。感赏自己明白自己容易受到某人的影响，心情不好，每当此刻我就会舒缓，感赏，让自己尽快抽离，想好的一面。感赏儿子今天在我提醒他事情时，告诉我谢谢妈妈对我的提醒我明白了，而不是说我啰嗦，管事情，孩子更懂事了，懂得感恩了。投射父母
  • 《中华小厨师》单行VS爱藏：姜是老的辣，书是新的好 cicoky
    《汉书·郦食其传》有曰：“王者以民为天，而民以食为天。”自古以来，吃饱饭是每一个人的基本要求，而吃好饭却是每一个人的最终追求。于是，厨师这一职业孕育而生，其渊源之久，甚至可追溯到4000年前的奴隶时代。职业本身无贵贱，但职业能力却有高低之分。所以一家餐馆生意好不好，厨师的水平决定一切，而站在所有厨师顶端的就被称之为“特级厨师”。今天要说的就是一个关于“特级厨师刘昴星”的故事。连载历程1995年第4
  • 读《人世间》有感 一0一
    这个寒假，就如同朋友圈中的一段话：一闭眼，一睁眼假期还有5天，在一闭眼一睁眼假期还有12天；再一闭眼一睁眼假期还有20天；不敢睡，不敢睡啊……受疫情影响，这个假期变得漫长又煎熬，我也无时无刻不关注着疫情的变化。当然这样的一个假期，我还真得要感谢周翔，因为他有个爱看书的习惯，所以家里有不少他看过的书，可以让我随意挑选，因此也让我的假期不至于那么无所事事。这次我选了一本梁晓声的《人世间》，作为一名语文
  • 2023-04-17|篮球女孩 长一木
    1小学抑或初中阶段，在课外书了解到她的故事。“篮球女孩”。当时佩服她的顽强，也对生命多了一丝敬畏。今天刚好在公众号看到，长大后的“篮球女孩”。佩服之余又满是心疼。网络侵删祝那素未蒙面的女孩，未来一切顺遂。
  • 使用Faiss进行高效相似度搜索 llzwxh888 faisspython
    在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
  • python是什么意思中文-在python中%是什么意思 编程大乐趣
    Python中%有两种：1、数值运算：%代表取模，返回除法的余数。如：>>>7%212、%操作符（字符串格式化，stringformatting），说明如下：%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+，-，''或0。+表示右对齐。-表示左对齐。''为一个空格，表示在正数的左侧填充一个空格，从而与负数对齐。0表示使用0填
  • Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Pythonpython开发语言大数据数据分析数据挖掘
    大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
  • python八股文面试题分享及解析(1) Shawn________ python
    #1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
  • 每日算法&面试题，大厂特训二十八天——第二十天（树） 肥学 ⚡算法题⚡面试题每日精进java算法数据结构
    目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
  • Python快速入门 —— 第三节：类与对象 孤华暗香 Python快速入门python开发语言
    第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
  • pyecharts——绘制柱形图折线图 2224070247 信息可视化pythonjava数据可视化
    一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
  • Python 实现图片裁剪（附代码） | Python工具 剑客阿良_ALiang
    前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
  • 【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师 华为od面试python
    华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
  • python os 环境变量 CV矿工 python开发语言numpy
    环境变量：环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里，比如数据库密码，个人账户密码，如果写进自己本机的环境变量里，程序用的时候通过os.environ.get（）取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量：os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
  • Python爬虫解析工具之xpath使用详解 eqa11 python爬虫开发语言
    文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中，数据提取是一个至关重要的环节。xpath作为一门
  • 2018-12-29 枫叶红时总多离别
    2018年12月29日星期六昨天老师就告诉我们，今天下午不用上课，是图书漂流活动会。我觉得很兴奋，好期待。到了下午，我帮好忙就到外面去买书，刚一出去，就有一大帮的大哥哥、大姐姐围着我问要不要买书，买一本书送一颗糖。我看到了一本《小老虎比上树》的书，问大姐姐多少钱，大姐姐说这本书原价13块，现在便宜4块钱也就是9块钱卖给你，我就把一张10块钱给她找，她找了我一块钱。我现在想想我今天只带了10块钱，现
  • 【华为OD技术面试真题 - 技术面】- python八股文真题题库（1） 算法大师 华为od面试python
    华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归（LinearRegression）模型形式：关键点：逻辑回归（LogisticRegression）模型形式：关键点：参数估计与评估：3.python浅拷贝及深拷贝浅拷贝（Shal
  • Linux的Initrd机制 被触发 linux
    Linux 的 initrd 技术是一个非常普遍使用的机制，linux2.6 内核的 initrd 的文件格式由原来的文件系统镜像文件转变成了 cpio 格式，变化不仅反映在文件格式上， linux 内核对这两种格式的 initrd 的处理有着截然的不同。本文首先介绍了什么是 initrd 技术，然后分别介绍了 Linux2.4 内核和 2.6 内核的 initrd 的处理流程。最后通过对 Lin
  • maven本地仓库路径修改 bitcarter maven
    默认maven本地仓库路径：C:\Users\Administrator\.m2 修改maven本地仓库路径方法：     1.打开E:\maven\apache-maven-2.2.1\conf\settings.xml     2.找到        
  • XSD和XML中的命名空间 darrenzhu xmlxsdschemanamespace命名空间
    http://www.360doc.com/content/12/0418/10/9437165_204585479.shtml http://blog.csdn.net/wanghuan203/article/details/9203621 http://blog.csdn.net/wanghuan203/article/details/9204337 http://www.cn
  • Java 求素数运算 周凡杨 java算法素数
    网络上对求素数之解数不胜数，我在此总结归纳一下，同时对一些编码，加以改进，效率有成倍热提高。 第一种：   原理: 6N(+-)1法         任何一个自然数，总可以表示成为如下的形式之一： 6N，6N+1，6N+2，6N+3，6N+4，6N+5 (N=0，1，2，…)   
  • java 单例模式 g21121 java
    想必单例模式大家都不会陌生，有如下两种方式来实现单例模式：   class Singleton { private static Singleton instance=new Singleton(); private Singleton(){} static Singleton getInstance() { return instance; }
  • Linux下Mysql源码安装 510888780 mysql
    1.假设已经有mysql-5.6.23-linux-glibc2.5-x86_64.tar.gz (1)创建mysql的安装目录及数据库存放目录       解压缩下载的源码包，目录结构，特殊指定的目录除外：           
  • 32位和64位操作系统 墙头上一根草 32位和64位操作系统
    32位和64位操作系统是指：CPU一次处理数据的能力是32位还是64位。现在市场上的CPU一般都是64位的，但是这些CPU并不是真正意义上的64 位CPU，里面依然保留了大部分32位的技术，只是进行了部分64位的改进。32位和64位的区别还涉及了内存的寻址方面，32位系统的最大寻址空间是2 的32次方= 4294967296（bit）= 4（GB）左右，而64位系统的最大寻址空间的寻址空间则达到了
  • 我的spring学习笔记10-轻量级_Spring框架 aijuans Spring 3
    一、问题提问：     → 请简单介绍一下什么是轻量级？     轻量级（Leightweight）是相对于一些重量级的容器来说的，比如Spring的核心是一个轻量级的容器，Spring的核心包在文件容量上只有不到1M大小，使用Spring核心包所需要的资源也是很少的，您甚至可以在小型设备中使用Spring。  
  • mongodb 环境搭建及简单CURD antlove WebInstallcurdNoSQLmongo
    一 搭建mongodb环境 1. 在mongo官网下载mongodb 2. 在本地创建目录 "D:\Program Files\mongodb-win32-i386-2.6.4\data\db" 3. 运行mongodb服务 [mongod.exe --dbpath "D:\Program Files\mongodb-win32-i386-2.6.4\data\
  • 数据字典和动态视图 百合不是茶 oracle数据字典动态视图系统和对象权限
    数据字典（data dictionary）是 Oracle 数据库的一个重要组成部分，这是一组用于记录数据库信息的只读（read-only）表。随着数据库的启动而启动,数据库关闭时数据字典也关闭   数据字典中包含   数据库中所有方案对象（schema object）的定义(包括表，视图，索引，簇，同义词，序列，过程，函数，包，触发器等等) 数据库为一
  • 多线程编程一般规则 bijian1013 javathread多线程java多线程
           如果两个工两个以上的线程都修改一个对象，那么把执行修改的方法定义为被同步的，如果对象更新影响到只读方法，那么只读方法也要定义成同步的。        不要滥用同步。如果在一个对象内的不同的方法访问的不是同一个数据，就不要将方法设置为synchronized的。
  • 将文件或目录拷贝到另一个Linux系统的命令scp bijian1013 linuxunixscp
    一.功能说明        scp就是security copy，用于将文件或者目录从一个Linux系统拷贝到另一个Linux系统下。scp传输数据用的是SSH协议，保证了数据传输的安全，其格式如下：        scp 远程用户名@IP地址：文件的绝对路径
  • 【持久化框架MyBatis3五】MyBatis3一对多关联查询 bit1129 Mybatis3
    以教员和课程为例介绍一对多关联关系，在这里认为一个教员可以叫多门课程，而一门课程只有1个教员教，这种关系在实际中不太常见，通过教员和课程是多对多的关系。   示例数据：   地址表：   CREATE TABLE ADDRESSES ( ADDR_ID INT(11) NOT NULL AUTO_INCREMENT, STREET VAR
  • cookie状态判断引发的查找问题 bitcarter formcgi
    先说一下我们的业务背景： 1.前台将图片和文本通过form表单提交到后台，图片我们都做了base64的编码，并且前台图片进行了压缩 2.form中action是一个cgi服务 3.后台cgi服务同时供PC，H5，APP 4.后台cgi中调用公共的cookie状态判断方法（公共的，大家都用，几年了没有问题） 问题：（折腾两天。。。。） 1.PC端cgi服务正常调用，cookie判断没
  • 通过Nginx,Tomcat访问日志(access log)记录请求耗时 ronin47
    一、Nginx通过$upstream_response_time $request_time统计请求和后台服务响应时间 nginx.conf使用配置方式： log_format main '$remote_addr - $remote_user [$time_local] "$request" ''$status $body_bytes_sent "$http_r
  • java-67- n个骰子的点数。 把n个骰子扔在地上，所有骰子朝上一面的点数之和为S。输入n，打印出S的所有可能的值出现的概率。 bylijinnan java
    public class ProbabilityOfDice { /** * Q67 n个骰子的点数 * 把n个骰子扔在地上，所有骰子朝上一面的点数之和为S。输入n，打印出S的所有可能的值出现的概率。 * 在以下求解过程中，我们把骰子看作是有序的。 * 例如当n=2时，我们认为（1，2）和（2，1）是两种不同的情况 */ private stati
  • 看别人的博客，觉得心情很好 Cb123456 博客心情
       以为写博客，就是总结，就和日记一样吧，同时也在督促自己。今天看了好长时间博客:    职业规划:    http://www.iteye.com/blogs/subjects/zhiyeguihua      android学习:    1.http://byandby.i
  • [JWFD开源工作流]尝试用原生代码引擎实现循环反馈拓扑分析 comsci 工作流
        我们已经不满足于仅仅跳跃一次，通过对引擎的升级，今天我测试了一下循环反馈模式，大概跑了200圈，引擎报一个溢出错误      在一个流程图的结束节点中嵌入一段方程，每次引擎运行到这个节点的时候，通过实时编译器GM模块，计算这个方程，计算结果与预设值进行比较，符合条件则跳跃到开始节点，继续新一轮拓扑分析，直到遇到
  • JS常用的事件及方法 cwqcwqmax9 js
    事件 描述 onactivate 当对象设置为活动元素时触发。 onafterupdate 当成功更新数据源对象中的关联对象后在数据绑定对象上触发。 onbeforeactivate 对象要被设置为当前元素前立即触发。 onbeforecut 当选中区从文档中删除之前在源对象触发。 onbeforedeactivate 在 activeElement 从当前对象变为父文档其它对象之前立即
  • 正则表达式验证日期格式 dashuaifu 正则表达式IT其它java其它
    正则表达式验证日期格式 function isDate(d){ var v = d.match(/^(\d{4})-(\d{1,2})-(\d{1,2})$/i); if(!v) { this.focus(); return false; } } <input value="2000-8-8" onblu
  • Yii CModel.rules() 方法 、validate预定义完整列表、以及说说验证 dcj3sjt126com yii
    public array rules () {return} array 要调用 validate() 时应用的有效性规则。 返回属性的有效性规则。声明验证规则，应重写此方法。 每个规则是数组具有以下结构：array('attribute list', 'validator name', 'on'=>'scenario name', ...validation
  • UITextAttributeTextColor = deprecated in iOS 7.0 dcj3sjt126com ios
    In this lesson we used the key "UITextAttributeTextColor" to change the color of the UINavigationBar appearance to white. This prompts a warning "first deprecated in iOS 7.0." Ins
  • 判断一个数是质数的几种方法 EmmaZhao Mathpython
    质数也叫素数，是只能被1和它本身整除的正整数，最小的质数是2，目前发现的最大的质数是p=2^57885161-1【注1】。 判断一个数是质数的最简单的方法如下： def isPrime1(n): for i in range(2, n): if n % i == 0: return False return True 但是在上面的方法中有一些冗余的计算，所以
  • SpringSecurity工作原理小解读 坏我一锅粥 SpringSecurity
      SecurityContextPersistenceFilter   ConcurrentSessionFilter   WebAsyncManagerIntegrationFilter   HeaderWriterFilter   CsrfFilter   LogoutFilter   Use
  • JS实现自适应宽度的Tag切换 ini JavaScripthtmlWebcsshtml5
    效果体验：http://hovertree.com/texiao/js/3.htm   该效果使用纯JavaScript代码，实现TAB页切换效果，TAB标签根据内容自适应宽度，点击TAB标签切换内容页。 HTML文件代码： <!DOCTYPE html> <html xmlns="http://www.w3.org/1999/xhtml"
  • Hbase Rest API : 数据查询 kane_xie RESThbase
    hbase（hadoop）是用java编写的，有些语言（例如python）能够对它提供良好的支持，但也有很多语言使用起来并不是那么方便，比如c#只能通过thrift访问。Rest就能很好的解决这个问题。Hbase的org.apache.hadoop.hbase.rest包提供了rest接口，它内嵌了jetty作为servlet容器。   启动命令：./bin/hbase rest s
  • JQuery实现鼠标拖动元素移动位置（源码+注释） 明子健 jqueryjs源码拖动鼠标
    欢迎讨论指正！   print.html代码： <!DOCTYPE html> <html> <head> <meta http-equiv=Content-Type content="text/html;charset=utf-8"> <title>发票打印</title> &l
  • Postgresql 连表更新字段语法 update qifeifei PostgreSQL
    下面这段sql本来目的是想更新条件下的数据，可是这段sql却更新了整个表的数据。sql如下： UPDATE tops_visa.visa_order SET op_audit_abort_pass_date = now() FROM tops_visa.visa_order as t1 INNER JOIN tops_visa.visa_visitor as t2 ON t1.
  • 将redis,memcache结合使用的方案? tcrct rediscache
    公司架构上使用了阿里云的服务，由于阿里的kvstore收费相当高，打算自建，自建后就需要自己维护，所以就有了一个想法，针对kvstore(redis)及ocs(memcache)的特点，想自己开发一个cache层，将需要用到list，set，map等redis方法的继续使用redis来完成，将整条记录放在memcache下，即findbyid，save等时就memcache，其它就对应使用redi
  • 开发中遇到的诡异的bug wudixiaotie bug
    今天我们服务器组遇到个问题： 我们的服务是从Kafka里面取出数据，然后把offset存储到ssdb中，每个topic和partition都对应ssdb中不同的key，服务启动之后，每次kafka数据更新我们这边收到消息，然后存储之后就发现ssdb的值偶尔是-2,这就奇怪了，最开始我们是在代码中打印存储的日志，发现没什么问题，后来去查看ssdb的日志，才发现里面每次set的时候都会对同一个key
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他