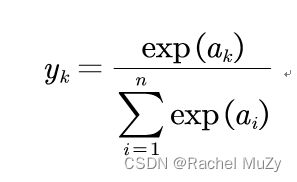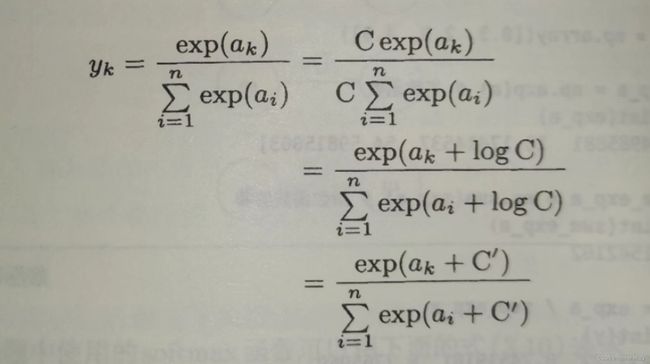【自学】深度学习入门 基于python的理论与实现 LESSON 2 ＜神经网络2＞

目录

前言

一、多维数组的运算

二、3层神经网络的实现

三、输出层的设计

1. 恒等函数

2.softmax函数

（1）基础softmax函数

（2）实现softmax的注意事项

（3）softmax特征

四、手写数字识别

1. MNIST数据集

2. 神经网络的推理处理 

总结

---

前言

本节继续学习神经网络的基础知识，并在结尾学习了书上的例子。

---

一、多维数组的运算

掌握了Numpy多维数组的运算，就可高校地实现神经网络。

下面介绍矩阵相乘：

import numpy as np

A = np.array([[2, 3], [4, 7], [1, 6]])
B = np.array([[1, 3, 2], [7, 4, 9]])
AB = np.dot(A, B)
print(AB)

结果：

[[23 18 31]
 [53 40 71]
 [43 27 56]]

神经网络的内积：

使用 np.dot（多维数组的点积），可以一次性计算出Y的结果。

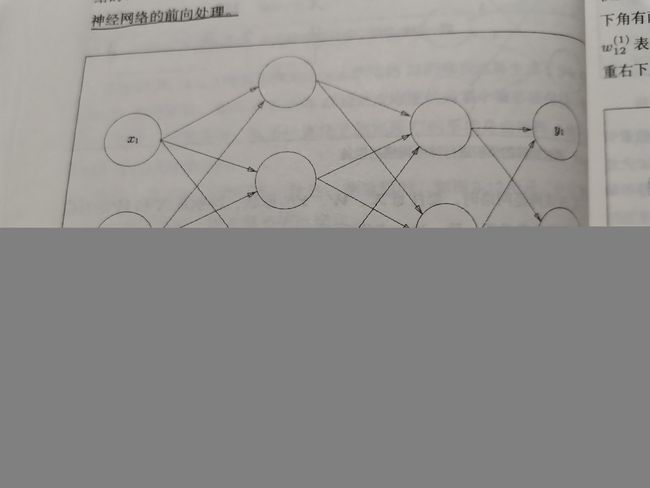
二、3层神经网络的实现

 

 示例：

三层神经网络的代码实现

import numpy as np

def identity_function(x):
    #阶跃函数，输出层的激活函数
    return x

def sigmoid(x):
    #隐藏层的激活函数
    y = 1 / (1 + np.exp(-x))
    return y
 
#第0层到第1层
x = np.array([1.0, 0.5])
w1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
b1 = np.array([0.1, 0.2, 0.3])
A1 = np.dot(x, w1) + b1
Z1 = sigmoid(A1)

#第1层到第二层
w2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
b2 = np.array([0.1, 0.2])
A2 = np.dot(Z1, w2) + b2
Z2 = sigmoid(A2)

#第2层到输出层
w3 = np.array([[0.1, 0.3], [0.2, 0.4]])
b3 = np.array([0.1, 0.2])
A3 = np.dot(Z2, w3) + b3
Y = identity_function(A3)

print(Y)

结果：

[0.31682708 0.69627909]

 注意：

输出层的激活函数，要根据求解问题的性质决定。一般地，回归问题用恒等函数，二元分类问题用sigmoid函数，多元分类问题可以使用softmax函数。

三、输出层的设计

1. 恒等函数

恒等函数会将输入按原样输出，对于输入的信息，不加以任何改动地直接输出。

2.softmax函数

（1）基础softmax函数

softmax函数用下式表示：

其中，n表示输出层神经元的个数，公式计算第k个神经元的输出yk.

代码实现：

import numpy as np

def softmax(a):
    exp_a = np.exp(a)
    sum_a = np.sum(exp_a)
    soft = exp_a / sum_a
    return soft

a = np.array([0.3, 2.9, 4.0, 5.3, 2.1, 0.8])
y = softmax(a)
print(y)

测试结果：

[0.00473883 0.06380236 0.19167288 0.70330467 0.02866825 0.00781301]

（2）实现softmax的注意事项

       上面的softmax函数有一定缺陷：溢出问题、softmax函数的实现中要进行指数函数的计算，但此时指数函数的值很容易变得非常大，例如e1000的结果会返回一个表示无穷大的inf。如果在这些超大值之间进行除法运算，结果会出现”不确定“情况。

因此，softmax函数可进行如下改进：

 其中，C'可以使用任何值，但为了防止溢出，一般会使用输入信号中的最大值。

示例：

import numpy as np

def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_a = np.sum(exp_a)
    soft = exp_a / sum_a
    return soft

a = np.array([1010, 1000, 990])
y = softmax(a)
print(y)

结果：

[9.99954600e-01 4.53978686e-05 2.06106005e-09]

（3）softmax特征

1. softmax函数的输出是0.0到1.0之间的实数，并且softmax函数的输出值的总和是1.因此把其输出解释为”概率“。可以说，通过使用softmax函数，我们可以用概率的方法处理问题。

2. 即使使用了softmax函数，各个元素之间的大小关系也不会改变。即a的各元素的大小关系和y的各元素大小关系没有改变。

3. 神经网络在进行分类时，输出层的softmax函数可以省略。在实际问题中，由于指数函数的运算需要一定的计算机运算量，因此输出层的softmax函数一般会被省略。

4. 机器学习的步骤可分为”学习“和”推理“两个阶段。如前所述，推理阶段一般会省略输出层的softmax函数。在输出层使用softmax函数是因为它和神经网络的学习有关。

5. 输出层的神经元数量需要根据待解决的问题来决定。对于分类问题，输出层的神经元数量一般设定为类别的数量。

四、手写数字识别

下载数据：

# coding: utf-8
try:
    import urllib.request
except ImportError:
    raise ImportError('You should use Python 3.x')
import os.path
import gzip
import pickle
import os
import numpy as np


url_base = 'http://yann.lecun.com/exdb/mnist/'
key_file = {
    'train_img':'train-images-idx3-ubyte.gz',
    'train_label':'train-labels-idx1-ubyte.gz',
    'test_img':'t10k-images-idx3-ubyte.gz',
    'test_label':'t10k-labels-idx1-ubyte.gz'
}

dataset_dir = os.path.dirname(os.path.abspath(__file__))
save_file = dataset_dir + "/mnist.pkl"

train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784


def _download(file_name):
    file_path = dataset_dir + "/" + file_name
    
    if os.path.exists(file_path):
        return

    print("Downloading " + file_name + " ... ")
    urllib.request.urlretrieve(url_base + file_name, file_path)
    print("Done")
    
def download_mnist():
    for v in key_file.values():
       _download(v)
        
def _load_label(file_name):
    file_path = dataset_dir + "/" + file_name
    
    print("Converting " + file_name + " to NumPy Array ...")
    with gzip.open(file_path, 'rb') as f:
            labels = np.frombuffer(f.read(), np.uint8, offset=8)
    print("Done")
    
    return labels

def _load_img(file_name):
    file_path = dataset_dir + "/" + file_name
    
    print("Converting " + file_name + " to NumPy Array ...")    
    with gzip.open(file_path, 'rb') as f:
            data = np.frombuffer(f.read(), np.uint8, offset=16)
    data = data.reshape(-1, img_size)
    print("Done")
    
    return data
    
def _convert_numpy():
    dataset = {}
    dataset['train_img'] =  _load_img(key_file['train_img'])
    dataset['train_label'] = _load_label(key_file['train_label'])    
    dataset['test_img'] = _load_img(key_file['test_img'])
    dataset['test_label'] = _load_label(key_file['test_label'])
    
    return dataset

def init_mnist():
    download_mnist()
    dataset = _convert_numpy()
    print("Creating pickle file ...")
    with open(save_file, 'wb') as f:
        pickle.dump(dataset, f, -1)
    print("Done!")

def _change_one_hot_label(X):
    T = np.zeros((X.size, 10))
    for idx, row in enumerate(T):
        row[X[idx]] = 1
        
    return T
    

def load_mnist(normalize=True, flatten=True, one_hot_label=False):
    """读入MNIST数据集
    
    Parameters
    ----------
    normalize : 将图像的像素值正规化为0.0~1.0
    one_hot_label : 
        one_hot_label为True的情况下，标签作为one-hot数组返回
        one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组
    flatten : 是否将图像展开为一维数组
    
    Returns
    -------
    (训练图像, 训练标签), (测试图像, 测试标签)
    """
    if not os.path.exists(save_file):
        init_mnist()
        
    with open(save_file, 'rb') as f:
        dataset = pickle.load(f)
    
    if normalize:
        for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].astype(np.float32)
            dataset[key] /= 255.0
            
    if one_hot_label:
        dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
        dataset['test_label'] = _change_one_hot_label(dataset['test_label'])
    
    if not flatten:
         for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].reshape(-1, 1, 28, 28)

    return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label']) 


if __name__ == '__main__':
    init_mnist()

1. MNIST数据集

读入MNIST数据：

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
from dataset.mnist import load_mnist
from PIL import Image


def img_show(img):
    pil_img = Image.fromarray(np.uint8(img))
    pil_img.show()

(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

img = x_train[0]
label = t_train[0]
print(label)  # 5

print(img.shape)  # (784,)
img = img.reshape(28, 28)  # 把图像的形状变为原来的尺寸
print(img.shape)  # (28, 28)

img_show(img)

结果：

 

2. 神经网络的推理处理 

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax


def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test


def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network


def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y


x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
    y = predict(network, x[i])
    p= np.argmax(y) # 获取概率最高的元素的索引
    if p == t[i]:
        accuracy_cnt += 1

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

 

---

 

总结

通过巧妙地使用NUMPY多维数组，可以高效地实现神经网络。