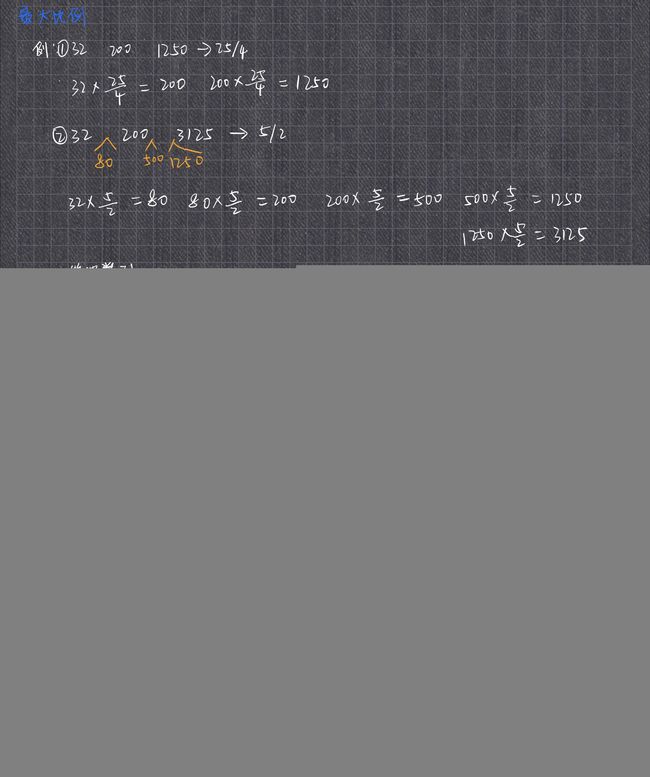2016年第七届蓝桥杯C/C++B组省赛题目及答案2

06. 方格填数

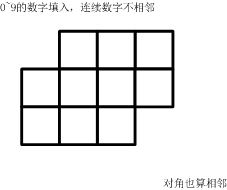
方格填数 如下的10个格子

    +--+--+--+ 
    |  |  |  | 
 +--+--+--+--+ 
 |  |  |  |  | 
 +--+--+--+--+
 |  |  |  | 
 +--+--+--+ 

（如果显示有问题，也可以参看图）
填入0~9的数字。
要求：连续的两个数字不能相邻。
（左右、上下、对角都算相邻）
一共有多少种可能的填数方案？
请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

答案：1580

方法一：

#include 
#include 
#include 
using namespace std;

int a[10] = {0,1,2,3,4,5,6,7,8,9};
int ans;

bool check()
{
	if (abs(a[0]-a[1]) == 1 ||
	    abs(a[0]-a[3]) == 1 || 
		abs(a[0]-a[4]) == 1 ||
		abs(a[0]-a[5]) == 1 ||
		
		abs(a[1]-a[2]) == 1 ||
		abs(a[1]-a[4]) == 1 ||
		abs(a[1]-a[5]) == 1 ||
		abs(a[1]-a[6]) == 1 ||
		
		abs(a[2]-a[5]) == 1 ||
		abs(a[2]-a[6]) == 1 ||
		
		abs(a[3]-a[4]) == 1 ||
		abs(a[3]-a[7]) == 1 ||
		abs(a[3]-a[8]) == 1 ||
		
		abs(a[4]-a[5]) == 1 ||
		abs(a[4]-a[7]) == 1 ||
		abs(a[4]-a[8]) == 1 ||
		abs(a[4]-a[9]) == 1 ||
		
		abs(a[5]-a[6]) == 1 ||
		abs(a[5]-a[8]) == 1 ||
		abs(a[5]-a[9]) == 1 ||
		
		abs(a[6]-a[9]) == 1 ||
		
		abs(a[7]-a[8]) == 1 ||
		
		abs(a[8]-a[9]) == 1 ) 
			return false;
	return true;
}

//考虑第k个位置，一般从0开始 
//这个套路要会默写！！ 
void f(int k)
{
	//出口
	if (k == 10)
	{
		bool b = check();
		if (b)
			ans++;
		return;
	}
	
	for (int i = k; i < 10; i++)
	{
		{  //尝试将位置i与位置k交换，以此确定k位的值 
			int t = a[i];
			a[i] = a[k];
			a[k] = t;
		}
		
	 	f(k+1);
	 
	 	{  //回溯 
	 		int t = a[i];
			a[i] = a[k];
			a[k] = t;
		}
	}  
}

int main()
{
	f(0); //手动全排列

/*	
	//方法二：自动全排列
	do
	{
		if (check())
		{
			ans++;
		}
	 } while (next_permutation(a,a+10)); 
*/
	cout << ans << endl;
	return 0; 
}

方法二：

#include 
#include 
using namespace std;

int a[5][6];
int vis[10];
int ans;

bool check(int i, int j)
{
	for (int x = i - 1; x <= i + 1; x++)
	{
		for (int y = j - 1; y <= j + 1; y++)
		{
			if (abs(a[x][y] - a[i][j]) == 1)
				return false;
		}
	}
	return true;
}

void f(int x,int y)
{
	if (x == 3 && y == 4)
	{
		ans++;
		return;
	}
	//从0~9中抓一个，即i 
	for (int i = 0; i < 10; i++)
	{
		if (vis[i] == 0)  //i没有被用过 
		{
			a[x][y] = i; //填数
			if (!check(x,y))
			{ //不合法，提前剪支，恢复并continue 
				a[x][y] = -10;
				continue;
			 } 
			vis[i] = 1;  //合法，标记为已访问 
			if (y == 4)
				f(x+1, 1);  //换行 
			else
				f(x,y+1);  //继续填右侧的格子 
			{
				vis[i] = 0;  //回溯 
				a[x][y] = -10; 
			} 
		}
	}
}

void init()
{
	for (int i = 0; i < 5; i++)
	{
		for (int j = 0; j < 6; j++)
		{
			a[i][j] = -10;
		}
	}
}

int main()
{
	init();
	f(1,2); 
	cout << ans << endl;
	return 0; 
}

07. 剪邮票

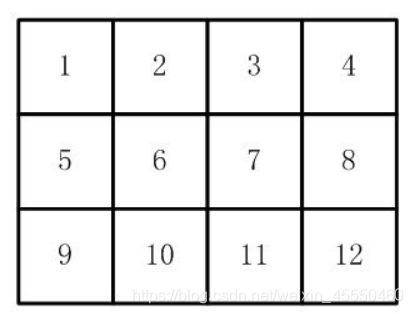
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来，要求必须是连着的。 （仅仅连接一个角不算相连）
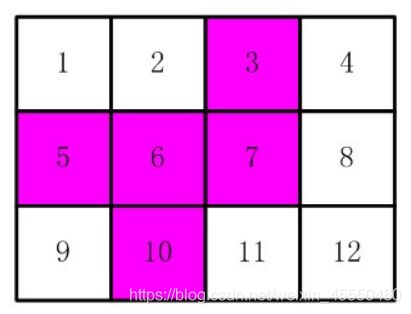
比如，【图2.jpg】，【图3.jpg】中，粉红色所示部分就是合格的剪取。
请你计算，一共有多少种不同的剪取方法。
请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

答案：116

思考：
此题和13年剪格子有相似之处，但是那个题的限制条件是格子数值之和为总和的一半，此题则限制只能是5个格子
单纯的dfs无法解决T字型连通方案
本题的解决办法是，找出任意5个格子，判断是否连通

#include 
#include 
#include 
#include 
#include 
using namespace std;

int a[] = {0,0,0,0,0,0,0,1,1,1,1,1};  //对他进行全排列，它的每个排列代表着12选5的一个方案 
int ans;

void dfs(int g[3][4], int i, int j)
{
	g[i][j] = 0;
	if (i-1>=0 && g[i-1][j]==1)  dfs(g, i-1, j);
	if (i+1<=2 && g[i+1][j]==1)  dfs(g, i+1, j);
	if (j-1>=0 && g[i][j-1]==1)  dfs(g, i, j-1);
	if (j+1<=3 && g[i][j+1]==1)  dfs(g, i, j+1);
}

//连通性检测
bool check()
{
	int g[3][4];
	memset(g,0,sizeof(g));
	//将某个排列映射到二维矩阵上 
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 4; j++)
		{
			if (a[i*4+j] == 1)
				g[i][j] = 1;
		}
	}
	//至此，g上面就有5个格子被标记为1，现在才用dfs来做连通性检查，要求只有一个连通块 
	//二维数组上的连通性检查是个经典问题，一定要会写！！！
	int cnt = 0;  //连通块的数目
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 4; j++)
		{
			if(g[i][j] == 1)
			{
				dfs(g,i,j);  //逮着一个1就由它开始往旁边搜
				cnt++; 
			}
		}
	}
	return cnt == 1; 
	 
 } 

set<string> s1;

void a2s(string &s)
{
	for (int i = 0; i < 12; i++)
	{
		s.insert(s.end(), a[i]+'0');
	}
 } 

bool isExist()
{
	string a_str;
	a2s(a_str);
	if (s1.find(a_str) == s1.end())  //没找着 
	{
		s1.insert(a_str);
		return false;
	}
	else
	{
		return true;
	}
 } 
 
void f (int k)
{
	if (k == 12)
	{
		if (!isExist() && check()) //要排除重复
		{
			ans++;
		}
	}
	for (int i = k; i < 12; i++)
	{
		{
			int t = a[i];
			a[i] = a[k];
			a[k] = t;
		}
		f(k+1);
		{
			int t = a[i];
			a[i] = a[k];
			a[k] = t;
		}
	}
 } 
 
bool check2(int path[12])
{
	int g[3][4];
	//将某个排列映射到二维矩阵上 
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 4; j++)
		{
			if (path[i*4+j] == 1)
				g[i][j] = 1;
			else
				g[i][j] = 0;
		}
	}
	//至此，g上面就有5个格子被标记为1，现在才用dfs来做连通性检查，要求只有一个连通块 
	//二维数组上的连通性检查是个经典问题，一定要会写！！！
	int cnt = 0;  //连通块的数目
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 4; j++)
		{
			if(g[i][j] == 1)
			{
				dfs(g,i,j);  //逮着一个1就由它开始往旁边搜
				cnt++; 
			}
		}
	}
	return cnt == 1; 
	 
 } 
 
bool vis[12];

void f2(int k, int path[12]) //抓取法生成全排列 
{
	if (k == 12)
	{
		if (check2(path))
		{
			ans++;
		}
	}
	for (int i = 0; i < 12; i++)
	{
		if (i > 0 && a[i] == a[i-1] && vis[i-1])  continue;  //现在准备选取的元素和上一个元素相同，但是上一个元素还没被使用，这种情况会引起重复 
		
		if (!vis[i])
		{  //没有被用过的元素可以被抓入到path 
			vis[i] = true;  //标记为已访问 
			path[k] = a[i];  //将a[i]填入到path[k]中 
			f2(k+1, path);  //递归 
			vis[i] = false;  //回溯 
		}
	}
 } 
 
int main()
{
/* 
	//方法一： 这个方法是排好了再去重，每一次都把数组变成字符串，时间上还是会很长
	f(0);
*/ 
/*	
	//方法二：用next_permutation生成全排列 
	do
	{
		if (check())
			ans++;
	}while (next_permutation(a,a+12));
*/	
	//方法三：
	int path[12];  //用来装被抓的元素 
	f2(0, path); 
	cout << ans << endl;
	return 0;	
}

08. 四平方和

四平方和定理，又称为拉格朗日定理：
每个正整数都可以表示为至多4个正整数的平方和。
如果把0包括进去，就正好可以表示为4个数的平方和。
比如：
5 = 0^2 + 0^2 + 1^2 + 2^2
7 = 1^2 + 1^2 + 1^2 + 2^2 （^符号表示乘方的意思）
对于一个给定的正整数，可能存在多种平方和的表示法。
要求你对4个数排序：
0 <= a <= b <= c <= d
并对所有的可能表示法按a,b,c,d 为联合主键升序排列，最后输出第一个表示法
程序输入为一个正整数N (N<5000000)
要求输出4个非负整数，按从小到大排序，中间用空格分开
例如，输入：
5
则程序应该输出：
0 0 1 2
再例如，输入：
12
则程序应该输出：
0 2 2 2
再例如，输入：
773535
则程序应该输出：
1 1 267 838
资源约定： 峰值内存消耗 <256M CPU消耗 < 3000ms
请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。
所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ，不能通过工程设置而省略常用头文件。
提交时，注意选择所期望的编译器类型。

思路：枚举+优化（通过减少变量和使用缓存来优化）

#include 
#include 
#include 
#include 
using namespace std;

int N;
map<int, int>cache;

int main()
{
	cin >> N;
	for (int c = 0; c*c <= N/2; c++)
	{
		for (int d = c; c*c+d*d <= N; d++)
		{
			if (cache.find(c*c+d*d) == cache.end())
				cache[c*c+d*d] = c;  //如果没找着再去存 
		}
	}
	for (int a = 0; a*a < N/4; a++)
	{
		for (int b = a; a*a+b*b <= N/2; b++)
		{
			if (cache.find(N-a*a-b*b) != cache.end())
			{	//能找着 
				int c = cache[N-a*a-b*b];
				int d = int(sqrt(N-a*a-b*b-c*c));
				cout << a << " "<< b << " "<< c << " "<< d << endl;
				return 0;
			}
		}
	}
	
}

09. 交换瓶子

有N个瓶子，编号 1 ~ N，放在架子上。
比如有5个瓶子：
2 1 3 5 4
要求每次拿起2个瓶子，交换它们的位置。
经过若干次后，使得瓶子的序号为：
1 2 3 4 5
对于这么简单的情况，显然，至少需要交换2次就可以复位。
如果瓶子更多呢？你可以通过编程来解决。
输入格式为两行：
第一行:
一个正整数N（N<10000）, 表示瓶子的数目
第二行：
N个正整数，用空格分开，表示瓶子目前的排列情况。
输出数据为一行一个正整数，表示至少交换多少次，才能完成排序。
例如，输入：
5
3 1 2 5 4
程序应该输出：
3
再例如，输入：
5
5 4 3 2 1
程序应该输出：
2
资源约定：
峰值内存消耗 < 256M
CPU消耗 < 1000ms
请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。
所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。
注意: main函数需要返回0 注意: 只使用ANSI C/ANSI C++标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ，不能通过工程设置而省略常用头文件。 提交时，注意选择所期望的编译器类型。

#include 
using namespace std;

int n; 
int a[10001];
int ans;

int pos(int x)
{
	for (int i = 1; i <= n; i++)
	{
		if (a[i] == x)  return i;
	}
	return -1;
}

void swap(int i, int j)
{
	int t = a[i];
	a[i] = a[j];
	a[j] = t;
}

int main()
{
	// 处理输入
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
	}
	// 遍历i：1-N 
	for (int i = 1; i <= n; i++)
	{
		// 如果a[i] = i，则表示已经到位
		if (a[i] == i)  continue;
		// 否则先找到i在a中的位置pos(i)，和i位交换——swap(a,pos(i),i)
		else
		{
			swap (pos(i), i);
			ans++;
		}
	}
	cout << ans << endl;
	return 0;
}

10. 最大比例

X星球的某个大奖赛设了M级奖励。 每个级别的奖金是一个正整数。
并且，相邻的两个级别间的比例是个固定值。
也就是说：所有级别的奖金数构成了一个等比数列。比如：
16,24,36,54
其等比值为：3/2
现在，我们随机调查了一些获奖者的奖金数。
请你据此推算可能的最大的等比值。
输入格式：
第一行为数字N，表示接下的一行包含N个正整数
第二行N个正整数Xi(Xi<1 000 000 000 000)，用空格分开。每个整数表示调查到的某人的奖金数额
要求输出：
一个形如A/B的分数，要求A、B互质。表示可能的最大比例系数
测试数据保证了输入格式正确，并且最大比例是存在的。
例如，输入：
3
1250 200 32
程序应该输出：
25/4
再例如，输入：
4
3125 32 32 200
程序应该输出：
5/2
再例如，输入：
3
549755813888 524288 2
程序应该输出：
4/1
资源约定：
峰值内存消耗 < 256M
CPU消耗 < 3000ms
请严格按要求输出，不要画蛇添足地打印类似：“请您输入…”的多余内容。
所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ，不能通过工程设置而省略常用头文件。 提交时，注意选择所期望的编译器类型。

#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long LL;

int N;
LL data[100];

//比值结构体
struct Ratio
{
	LL x,y;
	Ratio(LL _x, LL _y) : x(_x),y(_y)
	{
		LL _gcd = gcd(x,y);
		x /= _gcd;
		y /= _gcd;
	}
	
	//求最大公约数，这个一定要会写！ 
	LL gcd(LL a, LL b)
	{  
		if (b == 0)  return a;
		return gcd(b, a%b);
	}	
 }; 
 
vector<Ratio> ratios;
 
map<LL, map<LL,LL> > all_ex; //all_ex[x][pow] == x开pow次方 
map<LL, map<LL,LL> > all_log;  //all_log[x][y] == log_y_x, y的多少次方是x？

void init()
{
	for (int i = 2; i < 1e6; i++) //1e6表示10的6次方，因为最大的数是10的12次方，i表示的是底数 
	{
		LL cur = (LL) i*i;
		int pow = 2;
		while (cur < 1e12)
		{
			all_ex[cur][pow] = i;  // 第一轮：cur是i*i，cur开二次方等于i 
			all_log[cur][i] = pow;  //第一轮：以i为底数的二次方是cur 
			pow++; //然后pow变成三次方 
			cur *= i;
		}
	}
 } 
 
 /**
  * 对x开pow次方
  * @param x
  * @param pow
  * @return 
  */
LL extract(LL x, LL pow)
{
	if (pow == 1)  return x;
	if (x == 1)  return 1;
	if (all_ex[x].find(pow) != all_ex[x].end())  //意味着x可以开pow整数次方
		return all_ex[x][pow];
	else
		return -1; 
 } 
 
/**
 * 求log_base_x （找base的多少次方等于x） 
 * @param base
 * @param  
*/
LL log (LL base, LL x)
{
	
	if (base == x) return 1;
	if (all_log[x].find(base) != all_log[x].end())  //x作为指数，base作为基数，所以这里是base的多少次方。意味着可以得到一个k，base的k次方是x
		return all_log[x][base];
	return -1; 
 } 

int main()
{
	init();
	//处理输入
	cin >> N;
	for (int i = 0; i < N; i++)
	{
		cin >> data[i];
	}
	
	//排序
	sort(data,data+N);
	
	//处理只有两项的特殊情况 
	if(N==2)
	{
		Ratio ans = Ratio(data[1], data[0]);  //对base_x和base_y求比值（约分） 
		cout << ans.x << "/" << ans.y << endl;
		return 0;
	 } 
	
	//求两两比值，以分数形式存储，vector
	for (int i = 0; i < N-1; i++)
	{
		if (data[i+1] != data[i])  //去重 
			ratios.push_back(Ratio(data[i+1], data[i]));
	}
	
	//对第一个比值开 1 ~ pow(极限为40)次方，作为基数，
	//如果这个基数的分子分母的x1,x2...次方恰好是其他比值的分子分母
	//即如果这个基数也是其他比值的基数的话 
	//基数就是答案 
	for (int pow = 1; pow <= 40; pow++)
	{
		Ratio ra0 = ratios[0];
		LL x = ra0.x;
		LL y = ra0.y;
		LL base_x = extract(x,pow);  //对x开pow次方,作为基数，去尝试 
		LL base_y = extract(y,pow);  //对y开pow次方,作为基数，去尝试  
		if (base_x == -1 || base_y == -1)  continue;  //开不出，说明这个pow无效，continue
		
		//能开：就要去确认所有壁纸的分子都是base_x的整数次方，所有比值的分母都是base_y的整数次方
		//即 log_x = getPow(xx,base_x), log_y = getPow(yy,base_y)，要求必须是整数，且log_x==log_y
		bool all_match = true;
		for (int i = 1; i < ratios.size(); i++)
		{
			LL xx = ratios[i].x;
			LL yy = ratios[i].y;
			LL log_x = log(base_x, xx);
			LL log_y = log(base_y, yy);
			
			if (base_y==1 && yy==1)  log_y = log_x;  //因为1/1可以是很多次方，不能保证跟x的一样，下面的判断会出错 
			
			if (log_x == -1 || log_y == -1 || log_x != log_y)
			{
				all_match = false;
				break;
			}
		}
		if (all_match)
		{
			Ratio ans = Ratio(base_x, base_y);  //对base_x和base_y求比值（约分） 
			cout << ans.x << "/" << ans.y << endl;
			return 0;
		 } 
	}
}

小结

题目1：煤球数目
枚举+简单计算

题目2：生日蜡烛
等差数列求和
① 从一开始过生日吹蜡烛的年龄到最后一次过生日吹蜡烛，枚举两个年龄之间的差
② 枚举过生日吹蜡烛的次数
即：用等差数列的两种求和公式（两个公式要会背！！）

题目3：凑算式
全排列+check（注意坑点：要能通分）

题目4：快速排序
裸题（快速排序是必须要掌握的！！）

题目5：抽签
递归，要明确参数的含义和参数的变化方向

题目6：方格填数
全排列+check
（全排列也是必须要掌握的！！！）

题目7：剪邮票（**）
dfs解决不了T型组合，全排列+dfs求矩阵中的连通块
（全排列、dfs、求连通块都要掌握！）

题目8：四平方和
枚举+优化（hash缓存）

题目9：交换瓶子（**）
贪心

题目10：最大比例（****）
数学，等比数列，预处理
（任意抽两项出来都是公比的幂，那么所有的比值拿出来肯定有一个共同的基数，我们要找到一个最大的基数，就从小往大去开方，每开一次，能开出来，就拿去跟剩余的那些比值作比较，看它们是否蕴含了这个基数）
数值比较大，要做预处理