Physics-informed neural networks for inverse problems in nano-optics and metamaterials
论文信息
题目:hysics-informed neural networks for inverse problems in nano-optics and metamaterials
作者:Yuyao Chen, Lu Lu, George Em Karniadakis, and Luca Dal Negro
期刊会议:Computational Physics
年份:19
论文地址:
代码:
内容
动机
动机:
- 在强多光散射条件下,复杂多粒子几何中物理驱动的光散射微分模型的逆问题成为一个本质上不定的问题,利用传统方法不能满足预测需求
- 物理信息神经网络(PINNs)是近年来发展起来的一个通用框架,用于解决偏微分方程的正问题和反问题
- PINN仅使用一个训练数据集来实现所需的解决方案,从而减轻了替代方案中所需的大量训练数据集所带来的负担
问题定义:
逆问题:
f ( x ; ∂ u ^ ∂ x 1 , … , ∂ u ^ ∂ x d ; ∂ 2 u ^ ∂ x 1 ∂ x 1 , … , ∂ 2 u ^ ∂ x 1 ∂ x d ; … ; λ ) = 0 , x ∈ Ω f\left(\mathbf{x} ; \frac{\partial \hat{u}}{\partial x_{1}}, \ldots, \frac{\partial \hat{u}}{\partial x_{d}} ; \frac{\partial^{2} \hat{u}}{\partial x_{1} \partial x_{1}}, \ldots, \frac{\partial^{2} \hat{u}}{\partial x_{1} \partial x_{d}} ; \ldots ; \lambda\right)=0, \quad \mathbf{x} \in \Omega f(x;∂x1∂u^,…,∂xd∂u^;∂x1∂x1∂2u^,…,∂x1∂xd∂2u^;…;λ)=0,x∈Ω
其中 λ \lambda λ未知,其中loss定义为, L i \mathcal{L}_{i} Li,是初始点的 l o s s loss loss, L b \mathcal{L}_{b} Lb是边界点的 l o s s loss loss
L ( θ , λ ) = w f L f ( θ , λ ; T f ) + w i L i ( θ , λ ; T i ) + w b L b ( θ , λ ; T b ) \mathcal{L}(\boldsymbol{\theta}, \lambda)=w_{f} \mathcal{L}_{f}\left(\boldsymbol{\theta}, \lambda ; \mathcal{T}_{f}\right)+w_{i} \mathcal{L}_{i}\left(\boldsymbol{\theta}, \lambda ; \mathcal{T}_{i}\right)+w_{b} \mathcal{L}_{b}\left(\boldsymbol{\theta}, \lambda ; \mathcal{T}_{b}\right) L(θ,λ)=wfLf(θ,λ;Tf)+wiLi(θ,λ;Ti)+wbLb(θ,λ;Tb)
其中
L f ( θ , λ ; T f ) = 1 ∣ T f ∣ ∑ x ∈ T f ∥ f ( x ; ∂ u ^ ∂ x 1 , … , ∂ u ^ ∂ x d ; ∂ 2 u ^ ∂ x 1 ∂ x 1 , … , ∂ 2 u ^ ∂ x 1 ∂ x d ; … ; λ ) ∥ 2 2 L i ( θ , λ ; T i ) = 1 ∣ T i ∣ ∑ x ∈ T i ∥ u ^ ( x ) − u ( x ) ∥ 2 2 L b ( θ , λ ; T b ) = 1 ∣ T b ∣ ∑ x ∈ T b ∥ B ( u ^ , x ) ∥ 2 2 \begin{aligned} \mathcal{L}_{f}\left(\boldsymbol{\theta}, \lambda ; \mathcal{T}_{f}\right) &=\frac{1}{\left|\mathcal{T}_{f}\right|} \sum_{\mathbf{x} \in \mathcal{T}_{f}}\left\|f\left(\mathbf{x} ; \frac{\partial \hat{u}}{\partial x_{1}}, \ldots, \frac{\partial \hat{u}}{\partial x_{d}} ; \frac{\partial^{2} \hat{u}}{\partial x_{1} \partial x_{1}}, \ldots, \frac{\partial^{2} \hat{u}}{\partial x_{1} \partial x_{d}} ; \ldots ; \lambda\right)\right\|_{2}^{2} \\ \mathcal{L}_{i}\left(\boldsymbol{\theta}, \lambda ; \mathcal{T}_{i}\right) &=\frac{1}{\left|\mathcal{T}_{i}\right|} \sum_{\mathbf{x} \in \mathcal{T}_{i}}\|\hat{u}(\mathbf{x})-u(\mathbf{x})\|_{2}^{2} \\ \mathcal{L}_{b}\left(\boldsymbol{\theta}, \lambda ; \mathcal{T}_{b}\right) &=\frac{1}{\left|\mathcal{T}_{b}\right|} \sum_{\mathbf{x} \in \mathcal{T}_{b}}\|\mathcal{B}(\hat{u}, \mathbf{x})\|_{2}^{2} \end{aligned} Lf(θ,λ;Tf)Li(θ,λ;Ti)Lb(θ,λ;Tb)=∣Tf∣1x∈Tf∑∥∥∥∥f(x;∂x1∂u^,…,∂xd∂u^;∂x1∂x1∂2u^,…,∂x1∂xd∂2u^;…;λ)∥∥∥∥22=∣Ti∣1x∈Ti∑∥u^(x)−u(x)∥22=∣Tb∣1x∈Tb∑∥B(u^,x)∥22
根据PINN构建如下网络:建立微分方程解的代理模型,在更加 u u u求得 l o s s loss loss,最后最小化 l o s s loss loss求得参数 θ \theta θ和 λ \lambda λ
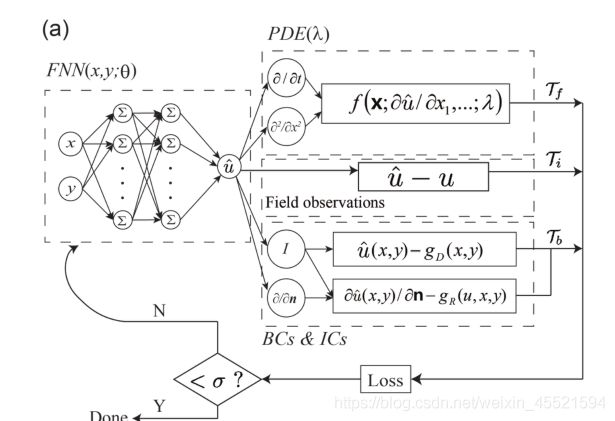
具体应用于均质有限尺寸的超材料问题:
∇ 2 E z ( x , y ) + ε r ( x , y ) k 0 2 E z = 0 \nabla^{2} E_{z}(x, y)+\varepsilon_{r}(x, y) k_{0}^{2} E_{z}=0 ∇2Ez(x,y)+εr(x,y)k02Ez=0
其中 E z E_{z} Ez是电厂的z分量, ε r ( x , y ) \varepsilon_{r} (x, y) εr(x,y)是空间相关的相对介电常数, k = 2 π / λ 0 k=2\pi /\lambda_{0} k=2π/λ0
创新: