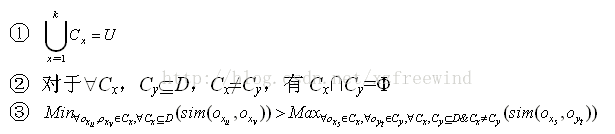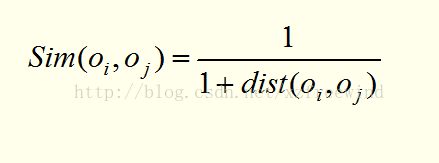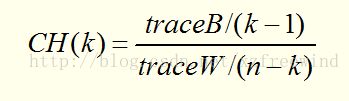大数据分析与挖掘
第一章 绪论
大数据分析与挖掘简介
大数据的四个特点(4v):容量(Volume)、多样性(Variety)、速度(Velocity)和价值
概念:数据分析是用适当的统计分析方法,对收集来的大量数据进行分析,提取有用信息和形成结论并对数据加以详细研究和概括总结的过程。数据分析可以分为三个层次,即描述分析、预测分析和规范分析。
数据挖掘:是指从数据集合中提取人们感兴趣的知识,这些知识是隐含的、实现未知的、潜在有用的信息。提取出来的知识一般可表示为概念、规则、规律、模式等形式。
大数据分析与挖掘主要技术
大数据分析与挖掘的过程一般分为如下几个步骤:
- 任务目标的确定
这一步骤主要是进行应用的需求分析,特别是要明确分析的目标,了 解与应用有关的先验知识和应用的最终目标。 - 目标数据集的提取
这一步骤是要根据分析和挖掘的目标,从应用相关的所有数据中抽取数据集,并选择全部数据属性中与目标最相关的属性子集。 - 数据预处理
这一步聚用来提高数据挖掘过程中所需数据的质量,同时也能够提高挖掘的效率。数据预处理过程包括数据清洗、 数据转换、数据集成、数据约减等操作。 - 建立适当的数据分析与挖掘模型
这一步骤包含了大量的分析与挖掘功能,如统计分析、分类和回归、聚类分析、关联规则挖掘、异常检测等。 - 模型的解释与评估
这一步骤主要见对挖掘出的模型进行解释,可以用可视化的方式来展示它们以利于人们的理解。 对模型的评估可以采用自动或半自动方式来进行,目的是找出用户真正感兴趣或有用的模型。 - 知识的应用
将挖掘出的知识以及确立的模型部署在用户的应用中。但这并不代表数据挖掘过程的结束,还需要一个不断反馈和迭代的过程,使模型和挖掘出的知识更加完善。
数据挖掘主要包括如下的功能
- 对数据的统计分析与特征描述
- 关联规则挖掘和相关性性分析
- 分类和回归
例如决策树、贝叶斯分类器、KNN分类器、组合分类算法等,回归则是对数值型的函数进行建模,常用于数值预测。 - 聚类分析
聚类的主要目标是使聚类内数据的相似性最大,聚类间数据的相似性最小 - 异常检测
第二章 数据特征分析与预处理
数据类型
2.1.1数据集类型
- 结构化数据
即行数据,存储在数据库里,可以用二维表结构来逻辑表达实现的数据,所有的数据都具有相同的模式。 - 半结构化数据
半结构化数据也具有一定的结构,但是没有像关系数据库中那样严格的模式定义。
常见的半结构化数据主要有XML文档和JSON数据 - 非结构化数据
非结构化数据没有预定义的数据了模型,涵盖各种文档、文本、图片、报表、图像、音频、视频
数据属性的类型
- 标称属性
标称属性类似于标签,其中的数字或字符只是用来对物体进行识别和分类,不具有顺序关系,也不存在比较关系。
对标称属性不能做加减乘除运算,可以分析各个属性值出现的次数
当标称属性类别或状态数为两个的时候,称为二元属性,也被称为布尔属性,如果二元属性的两种状态具有相同的重要程度,则称为对称的。 - 序数属性
这种属性值之间可以有顺序关系,例如:学生成绩可以分为优秀、良好、中等、及格和不及格;产品质量可以分为优秀、合格和不合格。这样的属性称为序数属性,在统计学中也称为定序变量
标称、二元和序数属性的取值都是定性的,它们只描述对象的特征,如高、低等定性信息,并不给出实际的大小。可以用来比较大小,但还不能反应不同等级间的差异程度,不能进行加减乘除等数学运算 - 数值属性
数值属性是可以度量的,通常用实数来表示。
数值属性可以分为区间标度属性和比率标度属性。
(1)区间标度属性不能进行比率运算,例如20℃不能说是10℃的两倍,类似区间标度属性的还有日历日期、华氏温度、智商、用户满意度打分等。这些区间标度属性共同的特点是:用相等的单位尺度度量,属性的值有序,可以为正、负或零。相等的数字距离代表所测量相等的数量差值,在统计学上也称为定距变量。
(2)比率标度属性由于存在绝对零点,因此可以进行比率的计算,即它可进行加减乘除运算。这一类数值属性称为比率标度属性,在统计学中称为定比变量,是应用最广泛的一类数值属性
属性类型总结
| 标称属性 | 序数属性 | 区间标度属性 | 比率标度属性 | |
|---|---|---|---|---|
| 频数统计 | √ | √ | √ | √ |
| 众数 | √ | √ | √ | √ |
| 顺序关系 | √ | √ | √ | |
| 中位数 | √ | √ | √ | |
| 平均数 | √ | √ | ||
| 量化差异 | √ | √ | ||
| 加减运算 | √ | √ | ||
| 乘除运算 | √ | |||
| 定义"真正零值" | √ |
数据的描述性特征
描述数据几种趋势的度量
1. 算术平均数 一个包含n个数值型数据的集合,其算术平均数的定义是:x ˉ = 1 n ∑ i = 1 n x i \bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_{i} xˉ=n1i=1∑nxi
(1)一个集合中的各个数据与算术平均数离差之和等于零,即: ∑ i = 1 n ( x i − x ˉ ) = 0 \sum_{i=1}^{n}(x_{i}-\bar{x})=0 ∑i=1n(xi−xˉ)=0 这个性质在数据的规范化中会被用到
(2)一个集合中的各个数据与算术平均数的离差平方之和是最小的。
算术平均数的缺点:容易受到集合中极端值或离群点的影响。
-
中位数
中位数是按照一定顺序排列后处于中间位置上的数据,中位数比算术平均数对于离群点的敏感度要低。当数据集合的分布呈现偏斜的时候,采用中位数作为集中趋势的度量更加有效 -
众数 (适合标称属性)
当数据的数量较大并且集中趋势比较明显的时候,众数更适合作为描述数据代表性水平的度量。 -
k百分位数
将一组数据从小到大排序,并计算相应的累计百分比,处于k%位置的值称为第k百分位数,用 X k % {X_{k\% }} Xk%表示。在一个集合里,有k%的数小于或等于 X k % {X_{k\% }} Xk%,有1-k%的数大于它。
例:设有一组数据:[-35,10,20,30,40,50,60,100],求它的25百分位数,即 X 25 % {X_{25\% }} X25%
一般有两种方法,分别是(n+1) * k%或者1+(n-1) * k%
X 25 % {X_{25\% }} X25%所在位置是1+(8-1)* 25%=2.75,处于第二个和第三个数之间,即10与20之间。如果采用线性插值的话 X 25 % {X_{25\% }} X25%=10+(20-10)* 0.75=17.5,中点:(10+20)/ 2=15 -
四分位数
四分位数是一种特殊的百分位数。
(1)第一四分位数Q1,又称“较小四分位数”,即25百分位数。
(2)第二四分位数Q2,就是中位数。
(3)第三四分位数Q3,又称“较大四分位数”,即75百分位数。
四分位数是比较常见的分析数据分布趋势的度量
描述数据离中趋势的度量
- 极差
极差是指一组数据中最大值与最小值之差,又称范围误差或全距,用R表示。 - 四位数极差(IQR)
四分位数极差也称内距,计算公式IQR=Q3-Q1,即第三四分位数减去第一四分位数的差,反应了数据集合中间50%数据的变动范围。
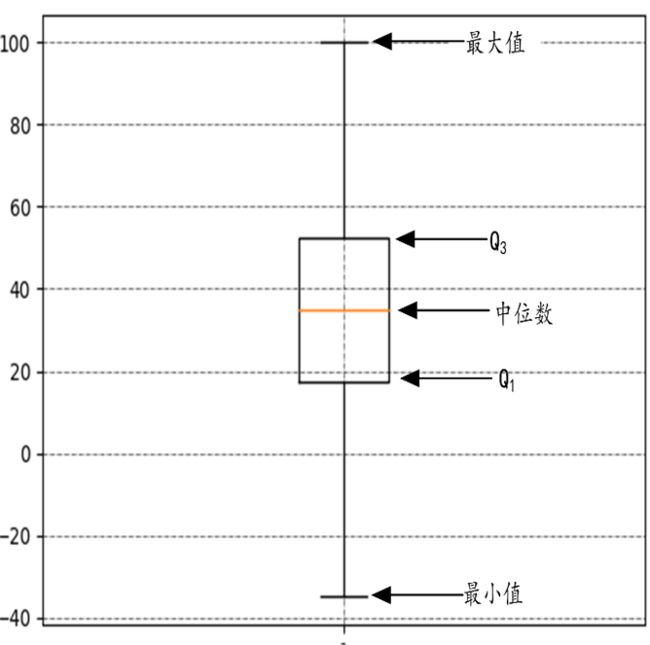
在探索性数据分析中,IQR可用于发现离群点,约翰·图基给了一个判定方法:超过Q3+1.5 * IQR或者低于Q1-1.5 * IQR的数据可能是离群点。
![]()
- 平均绝对离差
计算数据结合中各个数值与平均值的距离综合,然后取其平均数。
M A D = 1 n ∑ i = 1 n ∣ x i − x ˉ ∣ MAD=\frac{1}{n}\sum_{i=1}^{n}|x_{i}-\bar{x}| MAD=n1i=1∑n∣xi−xˉ∣
- 方差和标准差
♦样本方差的计算公式:
总体的方差:
σ 2 = ∑ ( X − μ ) 2 N {\sigma ^2}{\rm{ = }}\frac{{\sum {{{(X - \mu )}^2}} }}{N} σ2=N∑(X−μ)2
样本方差:
s 2 = 1 n − 1 ∑ i = 1 n ( x i − x ‾ ) 2 {s^2}{\rm{ = }}\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{({x_i} - \overline x )}^2}} s2=n−11i=1∑n(xi−x)2
♦标准差
标准差=方差的算数平方根
5. 离散系数
离散系数又称变异系数,样本变异系数是样本标准差与样本平均数之比:
C v = s x − {{\rm{C}}_{\rm{v}}} = \frac{s}{{\mathop x\limits^ - }} Cv=x−s
数据分布形态的度量
皮尔逊偏态系数
s k 1 = x − − M 0 s s{k_1} = \frac{{\mathop x\limits^ - - {M_0}}}{s} sk1=sx−−M0 或者 s k 2 = 3 ( x − − M d ) s s{k_2} = \frac{{3(\mathop x\limits^ - - {M_d})}}{s} sk2=s3(x−−Md)
其中,$\mathop x\limits^ - \$ 是平均数,$\{M_0}\ 是 重 数 , 是重数, 是重数,\{M_d}\$是中位数,s是样本标准差
数据的峰度及度量
峰度用于衡量数据分布的平坦度,它以标准正态分布作为比较的基准。峰度的度量使用峰度系数:
k = 1 n ∑ i = 1 n ( x i − x ˉ ) 4 ( 1 n ∑ i = 1 n ( x i − x ˉ ) ) 2 − 3 k = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^{4}}{(\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x}))^{2}}-3 k=(n1∑i=1n(xi−xˉ))2n1∑i=1n(xi−xˉ)4−3
k≈0,称为常峰态,接近于正态分布。
k<0,称为低峰态。
k>0,称为尖峰态。
数据偏度和峰度的作用
给定一个数据集合,通过计算它的偏度和峰度,可以符集数据分布与正态分布的差异,结合前面介绍的数据集中和离中趋势度量,就能够大致判断数据分布的形状等概要性信息,增加对数据的理解程度。
箱型图
数据的相关分析
相关分析
-
散点图
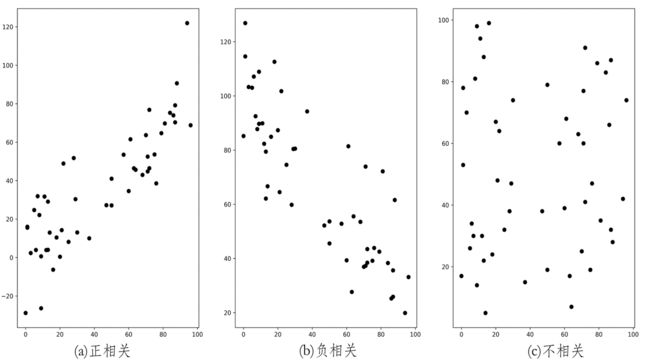
判断两个属性之间是否有相关性,可以首先通过散点图进行直观判断。
散点图是将两个属性的成对数据,绘制在直角坐标系中得到的一系列点,可以直观地描述属性间是否相关、相关的表现形式以及相关的密切程度。
-
相关系数
数据的各个属性之间关系密切程度的度量,主要是通过相关系数的计算与检验来完成的。
属性X和Y之间的样本协方差的计算公式:
c o v ( X , Y ) = ∑ i = 1 n ( X i − X − ) ( Y i − Y − ) n − 1 {\mathop{\rm cov}} (X,Y) = \frac{{\sum\limits_{i = 1}^n {({X_i} - \mathop X\limits^ - )({Y_i} - \mathop Y\limits^ - )} }}{{n - 1}} cov(X,Y)=n−1i=1∑n(Xi−X−)(Yi−Y−)
协方差的正负代表两个属性相关性的方向,而协方差的绝对值代表它们之间关系的强弱。 -
样本相关系数,协方差的大小与属性的取值范围、量纲都有关系,构成不同的属性对之间的协方差难以进行横向比较。为了解决这个问题,把协方差归一化,就得到样本相关系数的计算公式:
$$\r(X,Y) = \frac{{{\mathop{\rm cov}} (X,Y)}}{{{s_X}{s_Y}}}\$$
$\{s_X}{s_Y}\$标准差
相关系数消除了两个属性量纲的影响,它是无量纲的。相关系数的取值范围:-1<=r<=1;若0
卡方检验
可以用相关系数来分析两个数值型属性之间的相关性。对于两个标称属性(分类属性),他们之间的独立性检验可以使用卡方检验来推断。
χ 2 = ∑ ( O b s e r v e d − E x p e c t e d ) 2 E x p e c t e d {\chi ^2} = \sum {\frac{{{{(Observed - Expected)}^2}}}{{Expected}}} χ2=∑Expected(Observed−Expected)2
| 男 | 女 | 合计 | |
|---|---|---|---|
| 小说 | 250(90) | 200(360) | 450 |
| 非小说 | 50(210) | 1000(840) | 1050 |
| 合计 | 300 | 1200 | 1500 |
χ 2 {\chi ^2} χ2=507.93
自由度 dof=(r-1)(c-1) r和c分别是两个属性各个分类值的个数
自由度=(2-1)(2-1)
χ 2 {\chi ^2} χ2就是统计样本的实际观测值与理论推算值之间的偏离程度。Observed(观测),Expected(理论)
数据预处理
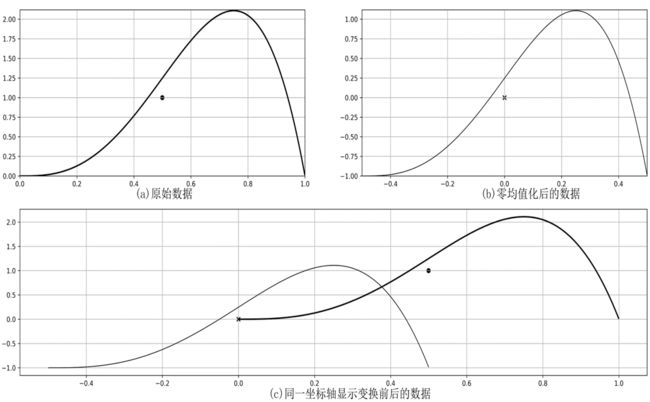
定义:对原始数据进行必要的清洗、集成、转换和归约等一系列处理,使数据达到进行只是获取所要求的规范和标准零均值化
将每一个属性的数据都减去这个属性的均值后,形成一个新数据集合,变换后各属性的数据之和与均值都为零。各属性的方差不发生变化,各属性间的协方差也不发生变化。
z分数变换
标准分数也叫z分数,用公式表示为:
z = x − x − s z = \frac{{x - \mathop x\limits^ - }}{s} z=sx−x−
其中x为原始数据, $\mathop x\limits^ - \$为样本均值,s为样本标准差。变换后数据的均值为0,方差为1。无量纲,数据尽量满足高斯分布。
z值表示袁术数据和样本均值之间的距离,是以标准差为单位计算的。原始数据低于标准值时,z为负数,反之为正数。
**缺点:**假如原始数据并没有呈高斯分布,标准化的数据分布效果不好
最小-最大规范化
最小-最大规范化又称离差标准化,是对原始数据的线性转换,将数据按照比例缩放至一个特定区间。假设原来数据分布在区间[min,max],要变换到区间[min’,max’],公式如下:
v ′ = m i n ′ + v − m i n m a x − m i n ( m a x ′ − m i n ′ ) v^{'}=min^{'}+\frac{v-min}{max-min}(max^{'}-min^{'}) v′=min′+max−minv−min(max′−min′)
独热编码
独热编码又称一位有效编码,用来对标称属性(分类属性)进行编码。
例,产品的颜色有{黑、白、蓝、黄}四种取值,分别用1、2、3、4来编码,假设有5个产品如下所示:
| ID | 颜色 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
问题:各个不同颜色值之间没有顺序关系,但从上述编码来看,颜色黑和黄之间的差异为3,而蓝和黄差异为1,似乎黄色和蓝色更相似一些。因此,按照这种简单的编码方式计算对象之间的差异时,就会得到错误的结果。
在上面的例子中,可以将一个颜色标称属性扩充为4个二元属性,分别对应黑、白、蓝、黄四种取值。对于每一个产品,它在这四个属性上只能有一个取1,其余三个都为0,所以称为独热编码
| ID | 黑色 | 白色 | 蓝色 | 黄色 |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1 |
任意两个不同颜色的产品之间的欧氏距离都是:
( 1 − 0 ) 2 + ( 0 − 1 ) 2 + ( 0 − 0 ) 2 + ( 0 − 0 ) 2 = 2 \sqrt{(1-0)^{2}+(0-1)^{2}+(0-0)^{2}+(0-0)^{2}}=\sqrt{2} (1−0)2+(0−1)2+(0−0)2+(0−0)2=2
可以看出,每一个标称属性扩充为独热编码后,在每一组新属性中,只有一个为1,其余同组的扩充属性值都为0,这就造成独热编码构成的向量较稀疏。
独热编码能够处理非连续性数值属性,并在一定程度上扩充了数值的特征(属性)。如在上例中颜色本身只是一个特征,经过独热编码以后,扩充成了四个特征。
使用独热编码,将离散属性的取值扩展到欧氏空间,回归、分类、聚类等很多数据挖掘算法对距离或相似度的计算是非常普遍的,而独热编码会让距离的计算更加合理。
在实际应用独热编码时,要注意它的引入有时会带来数据属性(维数)极大扩张的负面影响。
数据抽样技术
不放回简单随机抽样
例:设有一组数据: [11,13,16, 19,27, 36,43, 54, 62, 75], 现在想要从中不放回随机抽样5个数据,每个数据被抽中的概率分别为[0.1, 0.05, 0.05, 0.05, 0.05, 0.1, 0.1,0.1,0.1, 0.3]。
抽样过程如下。
(1 )根据待抽样数据的概率,计算以数组形式表示的累计分布概率edf,并规范化。
计算: cdf=[0.1,0.15,0.2,0.25,0.3, 0.4, 0.5, 0.6,0.7, 1]
规范化: cdf/=cdf[-1], 得到:[0.1,0.15,0.2,0.25, 0.3, 0.4, 0.5,0.6,0.7,1]
(2)根据还需抽样的个数,生成[0,1]的随机数数组x。
[0.04504848, 0.5299489, 0.0734825, 0.52341745, 0.17316974]
(3)将x中的随机数按照cdf值升序找到插入位置,形成索弓数组new。
[0,7,0,7,2]
(4)找出数组new中不重复的索引位置,作为本次抽样的位置索引。
[0 7 2]
(5)在概率数组p中,将已经抽样的索引位置置0。
P=[0, 0.05, 0., 0.05, 0.05, 0.1, 0.1, 0., 0.1, 0.3]
(6)重复上述步骤,知道输出指定数目的样本
水库抽样
输入:一组数据,其大小未知
输出:这组数据的K个均匀抽样
要求:
- 仅扫描数据一次
- 空间复杂性为O(K)【和抽样大小有关,和整个数据量无关,不可把所有数据都放在内存里进行抽样】
- 扫描到数据的前n个数字时(n>K),保存当前已扫描数据的K个均匀抽样
针对此种需求,水库抽样法应运而生
算法步骤:
- 申请一个长度为K的数组A保存抽样
- 保存首先接收到的K个元素
- 当接收到第 i 个新元素 t 时,以 K / i 的概率随机替换A中的元素(即生成 [ 1, i ]间随机数j,若 j ≤ K,则以 t 替换 A[ j ])
算法性质:
- 该采样是均匀的。
即在任何时候,接收到的大于K的n个数据,选出来的数都保证是均匀采样。
证明:
- 假设(n-1)次采样后, 缓冲区中k个样本的采样概率为/(−1);
- 在第n次采样中,缓冲区的样本被替换的概率为:/×1/=1/;
- 则第n次采样中,缓冲区的样本不会被替换的概率为: 1−1/=(−1)/
- 经过n次采样后,数据留在缓冲区的概率是下面两个概率乘积:
1.前(n-1)轮以后,数据在缓冲区中;
2.第n轮,没有被替换出去; - 概率是:/(−1)×(−1)/=/
- 归纳完毕
- 空间复杂性为O(K)
在整个的算法处理当中,我们只需要一个长度为K的数组保存抽样,剩下的计算概率的啥的空间都是常数的,因此空间复杂度为O(K)
主成分分析
- 主成分分析的目的和思想
主成分分析方法就是用较少数量的、彼此不相关的维度代替原来的维度,并能够解释数据所包含的大部分信息,这些不相关的新维度称为主成分。主成分实际上是一种降维方法,是将p维特征映射到m维上。
主成分分析的主要思想是将原来数量较多的具有一定相关性的维度,重新组合为一组数量较少的、相互不相关的综合维度(主成分)来替代原来的维度。
缺失值填充
将数据集中不含缺失值的变量(属性)称为完全变量,而将数据集中含有缺失值的变量(属性)称为不完全变量。
通常将数据缺失机制分为以下三种。
(1)完全随机缺失(Missins Compltely at Random,MCAR), 数据的缺失与不完全变量以及完全变量都是无关的。在这种情况下,某些数据的缺失与数据集合中其他数据的取值或者缺失没有关系,缺失数据仅是整个数据集合的一个随机子集合。 (例:硬件采集数据丢失)
(2)随机缺失( Missing at Random, MAR )。数据的缺天仅仅依赖于完全变量。随机缺失意味着数据缺失与缺失的数据值无关,但与数据在某些属性上的取值有关。例如,在分析客户购物行为的调查中,客户年龄这个属性的缺失值可能与本身的数值无关,但可能与客户的性别属性有关。客户收入属性上的缺失值,可能与他的职业属性有关,但与自身收入多少无关。
(3)非随机缺失( Not Missing at Random, NMAR)。 在不完全变量中数据的缺失依赖于不完全变量本身,这种缺失是不可忽略的。例如,在客户购物行为的调查中,一些高收入人群往往不填写收入值,这种缺失值与自身属性取值有关。
缺失值填充方法
- 均值填充法
将属性分为数值型和非数值利分别进行处理。如果缺失值是数值型,就用该属性在其他所有对象的取值的平均值来填充该缺失的变量值:如果缺失值是非数值型,则使用众数补齐该缺失的变量值。这种方法是建立在完全随机缺失的假设之上,而且会造成变量的方差和标准差变小。
这种方法的一个改进是“局部均值填充”,即使用有缺失值元组的“类别”的所有元组的平均值作为填充值。例如,某个职员工资额的缺失值,可以根据该员工的职称,求出具有同一职称的所有职工的平均工资值替换缺失值,以更加接近真实值。 - 回归填充法
回归填充法是把缺失属性作为因变量, 其他相关属性作为自变量,利用它们之间的关系建立回归模型来预测缺失值,并完成缺失值插补的方法。
回归填充的基本思想是利用辅助变量Xk与目标变量z的线性关系建立回归模型,从而利用已知的辅助变量的信息,对目标变量的缺失值进行估计。第i个缺失值的估计值可以表示为:
Z i = β 0 + ∑ k = 1 n β k X k i + ε Z_{i}=\beta _{0}+\sum_{k=1}^{n}\beta _{k}X_{ki}+\varepsilon Zi=β0+k=1∑nβkXki+ε
其中, β 0 \beta _{0} β0、 β k \beta _{k} βk为参数、 ε \varepsilon ε为残差,服从零均值正态分布。
问题是应该被估算的数据没有包含估计中的误差项,导致因变量与自变量之间的关系被过分识别。回归模型预测缺失数据最可能的值,但并不提供该预测值不确定性方面的信息。 - 热卡填充法(相似度: 欧式距离)
对于一个包含空值的对象,热卡填充法就是在完整数据中找到一个与它最相似的对象,用这个相似对象的值来填充。
特点:不同的问题可能会选用不同的标准对相似性进行判定。该方法的概念很简单,是利用数据间的关系来进行空值估计。这种方法的难点在于“距离” 或者“相似性”的定义。
平滑噪声
噪声数据:是指数据中存在着错误或异常(偏离异常值)的数据,这些数据对数据分析造成了干扰。即无意义数据,现阶段的意义已经扩展到包含所有难以被机器正确理解和翻译的数据,如非结构化文本。任何不可被源程序读取和运用的数据,不管是已经接受、存贮的还是改变的,都成为噪声。 噪声产生的原因有:数据收集工具的问题、数据输入错误、数据传输错误、技术限制、命名规则的不一致因为噪声对数据分析造成了干扰,所以我们需要去掉噪声或者平滑数据。现在介绍一种初级的方法:分箱
“分箱”是将属性的值域划分成若干连续子区间。如果一个属性值在某个子区间范围内,就把该值放进这个子区间所代表的“箱子”内。把所有待处理的数据(某列属性值)都放进箱子内,分别考察每一个箱子中的数据,采用某种方法分别对各个箱子中的数据进行处理。
对数据进行分箱主要有以下四种方法:
- 等深分箱法:将数据集按记录行数分箱,每箱具有相同的记录数,称为箱子的深度
- 等宽分箱法:将数据集在整个属性值的区间上平均分布,每个箱子的区间范围是一个常量,称为箱子宽度
在整个属性值的区间上平均分布,即每个箱的区间范围设定为一个常量,称为箱子的宽度。
简而言之,将变量的取值范围分为k个等宽的区间,每个区间当作一个分箱。例如年龄变量(0-100之间),可分成 [0,20],[20,40],[40,60],[60,80],[80,100]五个等宽的箱 - 最小熵法:在分箱时考虑因变量的取值,使得分箱后箱内达到最小熵
- 用户自定义区间法:根据数据特点,指定分箱的方法
每种分箱具体步骤:
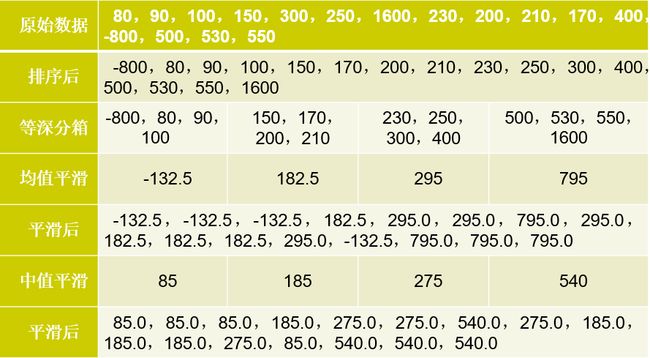
(1)首先排序数据,并将他们分到等深(等宽)的箱中;
(2)然后可以按箱的平均值、按箱中值或者按箱的边界等进行平滑
- 按箱的平均值平滑:箱中每一个值被箱中的平均值替换
- 按箱的中值平滑:箱中的每一个值被箱中的中值替换
- 按箱的边界平滑:箱中的最大和最小值被视为箱边界,箱中的每一个值被最近的边界值替换
等宽分箱:
使用等宽方法将数据组分为3个箱:11,13, 5,10,15,35,72,92,204,215,50,55
我们首先进行排序,排完序后为: 5,10,11,13,15,35,50,55,72,92,204,215
因为箱中数据宽度要相同,所以每个箱的宽度应是(215-5)/3=70
即要求箱中数据之差不能超过70.
所以答案为
Bin-1:5,10,11,13,15,35,50,55,72;
Bin-2:92;
Bin-3:204,215;
平均值平滑
已知一组价格数据:15,21,24,21,25,4,8,34,28
现用等宽(宽度为10)分箱方法对其进行平滑,以对数据中的噪声进行处理。
步骤:
(1)排序:4,8,15,21,21,24,25,28,34
(2)根据更宽分箱法,宽度为10
得到:
Bin-1:4,8
Bin-2:15,21,21,24,
Bin-3:28,34
(3)根据平均值平滑的定义:箱中的每一个值被箱中的平均值替换
(3)得到结果:
Bin-1:6,6
Bin-2:21,21,21,21,21
Bin-3:31,31,31
边界平滑
Bin-1:4,8
Bin-2:15,25,25,25,25( |15-21|=6,|25-21|=4,|25-24|=1)
Bin-3:28,34
第三章 关联规则挖掘
关联规则挖掘可以让我们从数据集中发现项与项(item 与 item)之间的关系,它在我们的生活中有很多应用场景,“购物篮分析”就是一个常见的场景,这个场景可以从消费者交易记录中发掘商品与商品之间的关联关系,进而通过商品捆绑销售或者相关推荐的方式带来更多的销售量。所以说,关联规则挖掘是个非常有用的技术。
搞懂关联规则中的几个概念
举一个超市购物的例子,下面是几名客户购买的商品列表:
| 订单编号 | 购买的商品 |
|---|---|
| 1 | 牛奶、面包、尿布 |
| 2 | 可乐、面包、尿布、啤酒 |
| 3 | 牛奶、尿布、啤酒、鸡蛋 |
| 4 | 面包、牛奶、尿布、啤酒 |
| 5 | 面包、牛奶、尿布、可乐 |
支持度计数
给出X在T中出现次数的定义: σ ( X ) = ∣ { t i ∣ X ⊆ t i , t i ∈ T } ∣ \sigma(X)=|\left \{ t_{i}|X\subseteq t_{i},t_{i}\in T \right \}| σ(X)=∣{ti∣X⊆ti,ti∈T}∣
支持度
支持度是个百分比,它指的是某个商品组合出现的次数与总次数之间的比例。
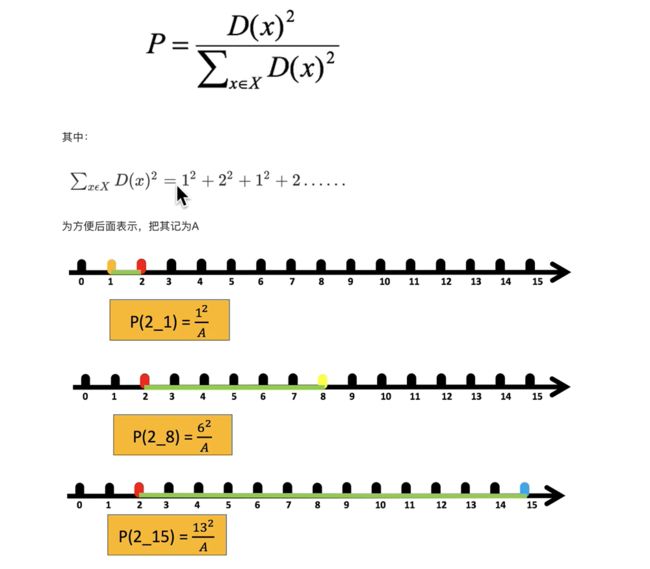
支持度: s u p ( X ) = σ ( X ) N sup(X)=\frac{\sigma (X)}{N} sup(X)=Nσ(X)
在这个例子中,我们能看到“牛奶”出现了 4 次,那么这 5 笔订单中“牛奶”的支持度就是 4/5=0.8。
同样“牛奶 + 面包”出现了 3 次,那么这 5 笔订单中“牛奶 + 面包”的支持度就是 3/5=0.6
置信度
c o n ( A − > B ) = σ ( A ∪ B ) σ ( A ) con(A->B)=\frac{\sigma (A\cup B)}{\sigma (A)} con(A−>B)=σ(A)σ(A∪B)
它指的就是当你购买了商品 A,会有多大的概率购买商品 B
置信度(牛奶→啤酒)=2/4=0.5,代表如果你购买了牛奶,有多大的概率会购买啤酒?
置信度(啤酒→牛奶)=2/3=0.67,代表如果你购买了啤酒,有多大的概率会购买牛奶?
置信度是个条件概念,就是说在 A 发生的情况下,B 发生的概率是多少。
提升度
我们在做商品推荐的时候,重点考虑的是提升度,因为提升度代表的是“商品 A 的出现,对商品 B 的出现概率提升的”程度。
提升度 (A→B)= 置信度 (A→B)/ 支持度 (B)
L i f t ( A , B ) = c o n ( A − > B ) s u p ( B ) Lift(A,B)=\frac{con(A->B)}{sup(B)} Lift(A,B)=sup(B)con(A−>B)
这个公式是用来衡量 A 出现的情况下,是否会对 B 出现的概率有所提升。
所以提升度有三种可能:
提升度 (A→B)>1:代表有提升,A和B是正相关的;
提升度 (A→B)=1:代表有没有提升,也没有下降,A和B独立;
提升度 (A→B)<1:代表有下降,A和B是负相关。
兴趣因子
Lift是对置信度的一种“修正”:考虑了规则后件的支持度。对于二元属性来说,List与兴趣因子等价。
I ( A , B ) = s u p ( A , B ) s u p ( A ) ∗ s u p ( B ) = N ∗ σ ( A , B ) σ ( A ) ∗ σ ( B ) I(A,B)=\frac{sup(A,B)}{sup(A)*sup(B)}=\frac{N*\sigma (A,B)}{\sigma(A) *\sigma(B) } I(A,B)=sup(A)∗sup(B)sup(A,B)=σ(A)∗σ(B)N∗σ(A,B)
兴趣因子I(A,B)>1:A和B是正相关的;
兴趣因子I(A,B)=1:A和B独立;
兴趣因子I(A,B)<1:A和B是负相关
Apriori 的工作原理
首先我们把上面案例中的商品用 ID 来代表,牛奶、面包、尿布、可乐、啤酒、鸡蛋的商品 ID 分别设置为 1-6,上面的数据表可以变为:| 订单编号 | 购买的商品 |
|---|---|
| 1 | 1、2、3 |
| 2 | 4、2、3、5 |
| 3 | 1、3、5、6 |
| 4 | 2、1、3、5 |
| 5 | 2、1、3、4 |
Apriori 算法其实就是查找频繁项集 (frequent itemset) 的过程,所以首先我们需要定义什么是频繁项集。
频繁项集就是支持度大于等于最小支持度 (Min Support) 阈值的项集,所以小于最小值支持度的项目就是非频繁项集,而大于等于最小支持度的的项集就是频繁项集。
项集这个概念,英文叫做 itemset,它可以是单个的商品,也可以是商品的组合。
我们再来看下这个例子,假设我随机指定最小支持度是 50%,也就是 0.5。
我们来看下 Apriori 算法是如何运算的:
首先,我们先计算单个商品的支持度,也就是得到 K=1 项的支持度:
| 商品项集 | 支持度 |
|---|---|
| 1 | 4/5 |
| 2 | 4/5 |
| 3 | 5/5 |
| 4 | 2/5 |
| 5 | 3/5 |
| 6 | 1/5 |
因为最小支持度是 0.5,所以你能看到商品 4、6 是不符合最小支持度的,不属于频繁项集,于是经过筛选商品的频繁项集就变成:
| 商品项集 | 支持度 |
|---|---|
| 1 | 4/5 |
| 2 | 4/5 |
| 3 | 5/5 |
| 5 | 3/5 |
在这个基础上,我们将商品两两组合,得到 k=2 项的支持度:
| 商品项集 | 支持度 |
|---|---|
| 1,2 | 3/5 |
| 1,3 | 1/5 |
| 1,5 | 2/5 |
| 2,3 | 4/5 |
| 2,5 | 2/5 |
| 3,5 | 3/5 |
我们再筛掉小于最小值支持度的商品组合,可以得到:
| 商品项集 | 支持度 |
|---|---|
| 1,2 | 3/5 |
| 2,3 | 4/5 |
| 3,5 | 3/5 |
我们再将商品进行 K=3 项的商品组合,可以得到:
| 商品项集 | 支持度 |
|---|---|
| 1,2,3 | 3/5 |
| 2,3,5 | 2/5 |
| 1,2,5 | 1/5 |
再筛掉小于最小值支持度的商品组合,可以得到:
| 商品项集 | 支持度 |
|---|---|
| 1,2,3 | 3/5 |
通过上面这个过程,我们可以得到 K=3 项的频繁项集{1,2,3},也就是{牛奶、面包、尿布}的组合。
Apriori 算法的递归流程:
1、K=1,计算 K 项集的支持度;
2、筛选掉小于最小支持度的项集;
3、如果项集为空,则对应 K-1 项集的结果为最终结果。
否则 K=K+1,重复 1-3 步。
Apriori 的改进算法:FP-Growth 算法
Apriori 在计算的过程中有以下几个缺点:
1、可能产生大量的候选集。因为采用排列组合的方式,把可能的项集都组合出来了;
2、每次计算都需要重新扫描数据集,来计算每个项集的支持度。
所以 Apriori 算法会浪费很多计算空间和计算时间,为此人们提出了 FP-Growth 算法:
1、创建了一棵 FP 树来存储频繁项集。在创建前对不满足最小支持度的项进行删除,减少了存储空间。
2、整个生成过程只遍历数据集 2 次,大大减少了计算量。
所以在实际工作中,我们常用 FP-Growth 来做频繁项集的挖掘,下面我给你简述下 FP-Growth 的原理。
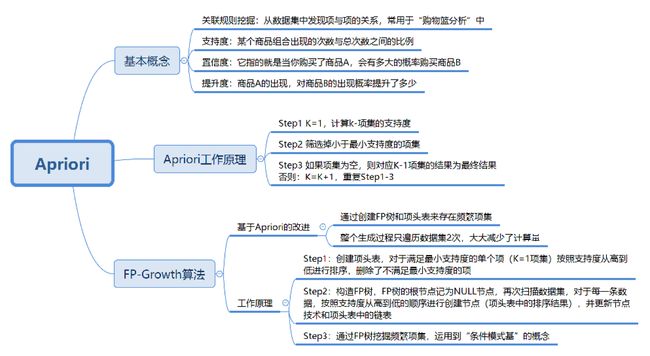
创建项头表(item header table)
创建项头表的作用是为 FP 构建及频繁项集挖掘提供索引
这一步的流程是先扫描一遍数据集,对于满足最小支持度的单个项(K=1 项集)按照支持度从高到低进行排序,这个过程中删除了不满足最小支持度的项。(第一步遍历数据集就删除了不满足最小支持度的项,降低了时间复杂度;同时降序排列可以公用祖先节点–null点)
项头表包括了项目、支持度,以及该项在 FP 树中的链表。初始的时候链表为空。
| 项 | 支持度 | 链表 |
|---|---|---|
| 尿布 | 5 | |
| 牛奶 | 4 | |
| 面包 | 4 | |
| 啤酒 | 3 |
构造 FP 树
FP 树的根节点记为 NULL 节点。
整个流程是需要再次扫描数据集,对于每一条数据,按照支持度从高到低的顺序进行创建节点(也就是第一步中项头表中的排序结果),如果有共用的祖先,则对应的公用祖先节点计数加1,如果不存在就进行创建。直到所有的数据都出现在FP树中。
同时在创建的过程中,需要更新项头表的链表。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kXcIP5Wp-1616905728423)(https://img2020.cnblogs.com/blog/1971052/202102/1971052-20210225201523101-109973184.png)]
构建子树
- 假设已经完成创建项头表的工作,省略count+1
- 扫描数据集,按照项头表排列好的结果,一次创建节点
- 因为尿布出现在所有订单中,没有例外情况,所以这只有一个子节点
- 因为牛奶出现在尿布中的所有订单里,所以只有一个子节点
- 由表中数据可得,在出现牛奶的订单中,面包出现的情况,分为两种,
1)出现3次面包,出现在有牛奶的订单中
2)出现一次面包,出现在没有牛奶的订单中
故,生成两个子节点 - 后续内容属于迭代内容,自行体会
通过 条件模式基挖掘频繁项集
我们就得到了一个存储频繁项集的 FP 树,以及一个项头表。我们可以通过项头表来挖掘出每个频繁项集。
具体的操作会用到一个概念,叫“条件模式基”,它指的是以要挖掘的节点为叶子节点,自底向上求出 FP 子树,然后将 FP 子树的祖先节点设置为叶子节点之和。
我以“啤酒”的节点为例,从 FP 树中可以得到一棵 FP 子树,将祖先节点的支持度记为叶子节点之和,得到:
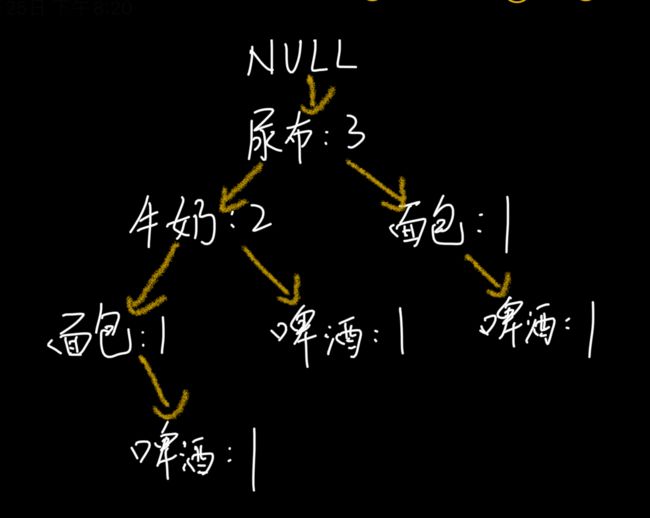
你能看出来,相比于原来的 FP 树,尿布和牛奶的频繁项集数减少了。这是因为我们求得的是以“啤酒”为节点的 FP 子树,也就是说,在频繁项集中一定要含有“啤酒”这个项。
你可以再看下原始的数据,其中订单 1{牛奶、面包、尿布}和订单 5{牛奶、面包、尿布、可乐}并不存在“啤酒”这个项,所以针对订单 1,尿布→牛奶→面包这个项集就会从 FP 树中去掉,针对订5 也包括了尿布→牛奶→面包这个项集也会从 FP 树中去掉,所以你能看到以“啤酒”为节点的 FP 子树,尿布、牛奶、面包项集上的计数比原来少了 2。
条件模式基不包括“啤酒”节点,而且祖先节点如果小于最小支持度就会被剪枝,所以“啤酒”的条件模式基为空。
同理,我们可以求得“面包”的条件模式基为:
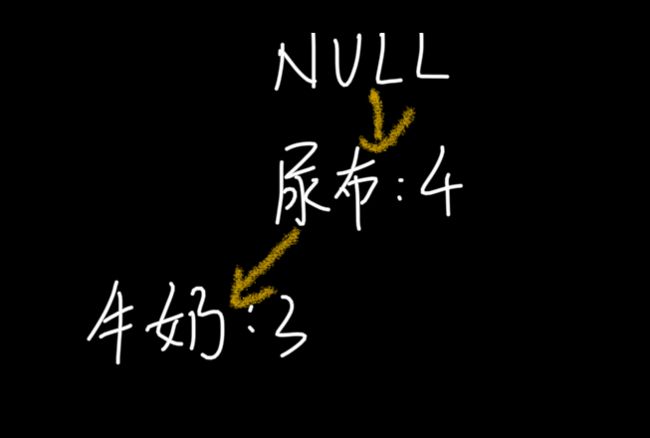
所以可以求得面包的频繁项集为{尿布,面包},{尿布,牛奶,面包}。同样,我们还可以求得牛奶,尿布的频繁项集,这里就不再计算展示。
FP-Growth 算法总结:
- 构建项头表,从高到底排序(以便有共同祖节点)
- 对数据集按照项头表顺序进行排序,然后从高到低递归绘制层次图
- 按照项头表,依据第2步结果,从低到高,重新按照节点原则构建层次图,得到条件模式基。
总结
1、关联规则算法是最常用的算法,通常用于“购物篮分析”,做捆绑推荐。
2、Apriori 算法在实际工作中需要对数据集扫描多次,会消耗大量的计算时间
3、针对Apriori 算法时间复杂度高, FP-Growth 算法被提出来,通过 FP 树减少了频繁项集的存储以及计算时间。
4、原始模型往往是最接近人模拟的过程,但时间复杂度或空间复杂度高;于是人们就会提出新的方法,比如新型的数据结构,可以提高模型的计算速度。
5、FP Tree算法改进了Apriori算法的I/O瓶颈,巧妙的利用了树结构,这让我们想起了BIRCH聚类,BIRCH聚类也是巧妙的利用了树结构来提高算法运行速度。利用内存数据结构以空间换时间是常用的提高算法运行时间瓶颈的办法。
6、置信度和提升度是对频繁项集的一种验证,在筛选最优组合的时候,一般会设置最小支持度,最小置信度,这样频繁项集和关联关系都要满足这个条件。提升度 (A→B)= 置信度 (A→B)/ 支持度 (B),所以提升度是对满足前两者条件的另一种验证方式,这样避免一种情况:置信度(A->B)很高,是因为本身支持度(B)很高,实际上和A的出现关系不大。
多层关联规则挖掘算法
多层关联规则是一种基于概念分层的关联规则挖掘方法,概念分层是一种映射,它将底层概念映射到高层概念。概念层次结果通常会用概念树表示,按照一般到特殊的顺序以偏序的形式排列。
假设在事务数据库中出现的商品都是食品,他们分类信息的概念层次树有三层,分别代表牛奶或面包,牛奶又分成“牛乳”或者“乳制品”,再下层是各种品牌。

从概念层次树上第一层开始进行编码(不包括第零层:食品),例如,某个商品项的编码为112,第一个数表示“牛奶”类,第二个数1表示“牛乳”,第三个数2表示品牌的名字。这样再事务数据库中所有具体商品都被泛化到第三层,同类商品再这个层次上编码相同
概念泛化后的数据库T[1]
| TID | 项集 |
|---|---|
| T1 | {111,121,211,221} |
| T2 | {111,211,222,323} |
| T3 | {112,122,221,411} |
| T4 | {111,121} |
| T5 | {111,122,211,221,413} |
| T6 | {211,323,524} |
| T7 | {323,411,524,713} |
在第一层上挖掘频繁1-项集,每个项具有如下形式“1**”,···,“2**”等,在同一事务中合并相同的编码,设第一层的最小支持度计数为4,得到第一层上的频繁1-项集L1,1和频繁2-项集L[1,2]
第一层上的频繁1-项集L[1,1]
| 项集 | 支持度计数 |
|---|---|
| {1**} | 5 |
| {2**} | 5 |
第一层上的频繁2-项集L[1,2]
| 项集 | 支持度计数 |
|---|---|
| {1** ,2**} | 4 |
在第一层上可以得到“牛奶—>面包”的关联规则,继续挖掘第二层的频繁项集,在数据库T[1]中过滤掉非频繁的项,得到数据库T[2]
过滤后的数据库T[2]
| TID | 项集 |
|---|---|
| T1 | {111,121,211,221} |
| T2 | {111,211,222} |
| T3 | {112,122,221} |
| T4 | {111,121} |
| T5 | {111,122,211,221} |
| T6 | {211} |
如果这一层的最小支持度计数还设为4,则可能丢失部分关联规则,通常在较低层设置较低的最小支持度。设第二层的最小支持度计数为3,分别得到第二层的频繁1-项集、频繁2-项集、频繁3-项集
第二层上的频繁1-项集L[2,1]
| 项集 | 支持度计数 |
|---|---|
| {11*} | 5 |
| {12*} | 4 |
| {21*} | 4 |
| {22*} | 4 |
第二层上的频繁2-项集L[2,2]
| 项集 | 支持度计数 |
|---|---|
| {11 * ,12 * } | 4 |
| {11 * ,21 * } | 3 |
| {11 * ,22 * } | 4 |
| {12 * ,22 * } | 3 |
| {21 * ,22 * } | 3 |
第二层上的频繁3-项集L[2,3]
| 项集 | 支持度计数 |
|---|---|
| {11 * ,12 * ,22 * } | 3 |
| {11 * ,21 * ,22 * } | 3 |
同理,可以得到第三层的频繁项集
第三层上的频繁1-项集L[3,1]
| 项集 | 支持度计数 |
|---|---|
| {111} | 4 |
| {211} | 4 |
| {221} | 3 |
第三层上的频繁2-项集L[3,2]
| 项集 | 支持度计数 |
|---|---|
| {111,211} | 3 |
上述过程挖掘的频繁项集都位于同一层上,在此基础上还可以挖掘跨层频繁项集。对上述算法稍作修改即可实现。
在挖掘跨层频繁项集的过程中,L[1,1]、L[1,2]和L[2,1]的生成过程同上,生成的候选3-项集的过程略有不同,不仅要从L[2,1]生成,还要加上L[1,1]一并生成,通过扫描T[2]后,得到新的频繁2-项集
新的第二层上的频繁2-项集L[2,2]
| 项集 | 支持度计数 |
|---|---|
| {11 * ,12 * } | 4 |
| {11 * ,21 * } | 3 |
| {11 * ,22 * } | 4 |
| {12 * ,22 * } | 3 |
| {21 * ,22 * } | 3 |
| {11 * ,2 * * } | 4 |
| {12 * ,2 * * } | 3 |
| {21*,1**} | 3 |
| {22*,1**} | 4 |
从新的L[2,2]可以看出,产生了跨层的频繁2-项集。需要注意的是,具有祖先和后代关系的两个项不能入选频繁2-项集。
新的第二层上的频繁3-项集L[2,3]
| 项集 | 支持度计数 |
|---|---|
| {11 * ,12 * ,22 * } | 3 |
| {11 * ,21 * ,22 * } | 3 |
| {21 * ,22 * ,1 * * } | 3 |
得到的L[3,1]和上边L[3,1]相同,产生候选2-项集要与L[1,1]和L[2,1]一起考虑,最终得到的L[3,2]
新的第三层上的频繁2-项集L[3,2]
| 项集 | 支持度计数 |
|---|---|
| {111,211} | 3 |
| {111,21 * } | 3 |
| {111,22 * } | 3 |
| {111,2 * * } | 4 |
| {11 * ,211} | 3 |
| {1 * * ,211} | 3 |
具有祖先和后代关系的两个项不会被加入频繁项集。从L[3,2]生成候选3-项集,验证后,得到第三城的跨层频繁3-项集
新的第三层上的频繁3-项集L[3,3]
| 项集 | 支持度计数 |
|---|---|
| {111,21 * ,22 * } | 3 |
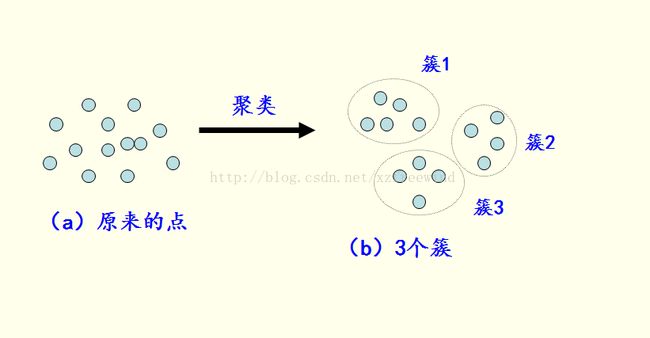
序列模式挖掘
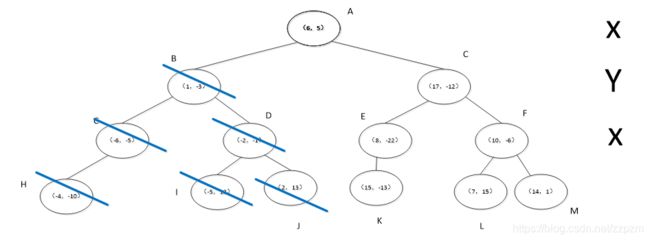
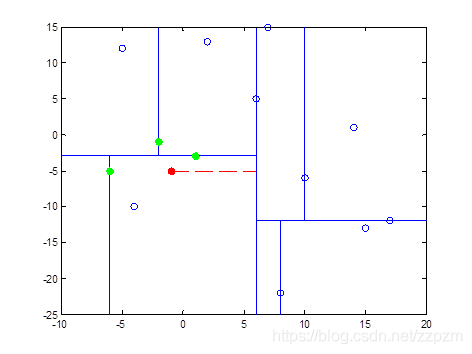
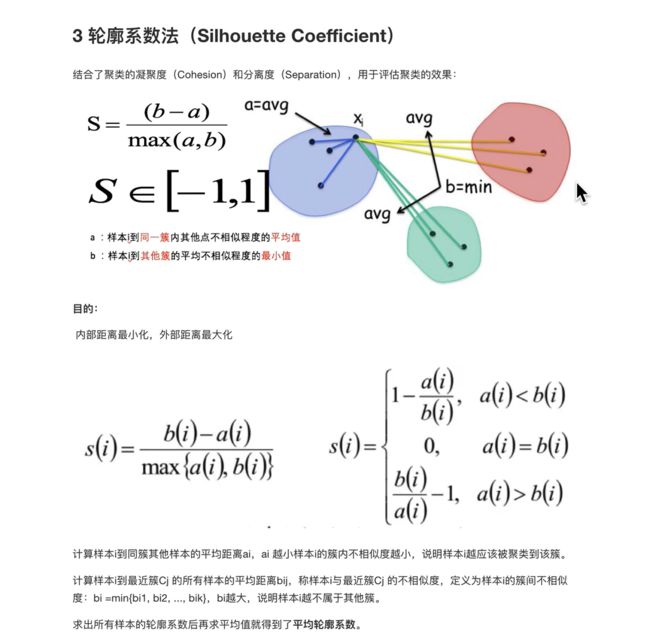
序列模式的定义 一个序列 s 2 s_{2} s2=< b 1 b_{1} b1, b 2 b_{2} b2,···, b n b_{n} bn>包括另一个 s 1 s_{1} s1=< a 1 a_{1} a1, a 2 a_{2} a2,···, a m a_{m} am>,如果存在整数1<= i 1 i_{1} i1< i 2 i_{2} i2<···< i m i_{m} im<=n,可得 a 1 ⊆ b i 1 a_{1}\subseteq b_{i_{1}} a1⊆bi1, a 2 ⊆ b i 2 a_{2}\subseteq b_{i_{2}} a2⊆bi2,···, a m ⊆ b i m a_{m}\subseteq b_{i_{m}} am⊆bim。例如,<(7)(3,8)(9)(4,5,6)(8)>有七个元素,序列长度为8,包括<(3)(4,5)(8)>,其中(3) ⊆ \subseteq ⊆(3,8),(4,5) ⊆ \subseteq ⊆ (4,5,6),(8) ⊆ \subseteq ⊆ (8)。<(3)(5)>不包含在<(3,5)>中,反之亦然。如果使用购物篮例子,假设每个项目集是一次购买的商品,那么前者表示第三项和第五项被一个接一个地购买,而后者表示第三项和第五项被一起购买。 序列模式地定义:如果定义序列数据库S是元组 L1=>C2=>L2=>C3=>L3=>C4=>L4······ 产生候选序列模式主要分成两步 L1=>C2=>L2=>C3=>L3=>C4=>L4······ 一组候选序列的产生是通过在先前扫描通过的序列模式上进行自我结合的。在第k次扫描的时候,只要每个它的每个length-(k-1)的子序列实在第k-1次扫描的时候找到的一个序列模式,那么这个序列就是候选序列。当在一次扫描的过程中没有发现候选序列或者没有候选序列的产生的时候算法就停止了。 如上图所示,在连接的过程中,种子序列<(1,2) 3>和种子序列<2 (3,4)>连接可产生候选4序列<(1,2)(3,4)>;和种子序列<2 3 5>连接可产生候选4序列<(1,2) 3 5>。其余的序列均不满足连接条件,在剪枝过程中,候选4序列<(1,2) 3 5>被减去,因为其连续子序列<1,3,5>不包含3序列模式集合L3中。 GSP算法存在的问题 FreeSpan算法优点 FreeSpan算法缺点 在PrefixSpan算法中的前缀prefix通俗意义讲就是序列数据前面部分的子序列。如果用严格的数学描述,前缀是这样的:对于序列A={a1,a2,…ana1,a2,…an}和序列B={b1,b2,…bmb1,b2,…bm},n≤mn≤m,满足a1=b1,a2=b2…an−1=bn−1,而an⊆bn,则称A是B的前缀。比如对于序列数据B= 看了前缀,我们再来看前缀投影,其实前缀投影这儿就是我们的后缀,有前缀就有后缀嘛。前缀加上后缀就可以构成一个我们的序列。下面给出前缀和后缀的例子。对于某一个前缀,序列里前缀后面剩下的子序列即为我们的后缀。如果前缀最后的项是项集的一部分,则用一个“_”来占位表示。 下面这个例子展示了序列 PrefixSpan算法思想 比如对应于我们第二节的例子,支持度阈值为50%。里面长度为1的前缀包括< a >, < b >, < c >, < d >, < e >, < f >,< g >我们需要对这6个前缀分别递归搜索找各个前缀对应的频繁序列。如下图所示,每个前缀对应的后缀也标出来了。由于g只在序列4出现,支持度计数只有1,因此无法继续挖掘。我们的长度为1的频繁序列为< a >, < b >, < c >, < d >, < e >,< f >。去除所有序列中的g,即第4条记录变成 现在我们开始挖掘频繁序列,分别从长度为1的前缀开始。这里我们以d为例子来递归挖掘,其他的节点递归挖掘方法和D一样。方法如下图,首先我们对d的后缀进行计数,得到{a:1, b:2, c:3, d:0, e:1, f:1,_f:1}。注意f和_f是不一样的,因为前者是在和前缀d不同的项集,而后者是和前缀d同项集。由于此时a,d,e,f,_f都达不到支持度阈值,因此我们递归得到的前缀为d的2项频繁序列为和。接着我们分别递归db和dc为前缀所对应的投影序列。首先看db前缀,此时对应的投影后缀只有<_c(ae)>,此时_c,a,e支持度均达不到阈值,因此无法找到以db为前缀的频繁序列。现在我们来递归另外一个前缀dc。以dc为前缀的投影序列为<_f>, <(bc)(ae)>, ,此时我们进行支持度计数,结果为{b:2, a:1, c:1, e:1, _f:1},只有b满足支持度阈值,因此我们得到前缀为dc的三项频繁序列为。我们继续递归以为前缀的频繁序列。由于前缀对应的投影序列<(_c)ae>支持度全部不达标,因此不能产生4项频繁序列。至此以d为前缀的频繁序列挖掘结束,产生的频繁序列为。 同样的方法可以得到其他以< a >, < b >, < c >, < e >, < f >为前缀的频繁序列。 PrefixSpan算法流程 输出:所有满足支持度要求的频繁序列集 1)找出所有长度为1的前缀和对应的投影数据库 2)对长度为1的前缀进行计数,将支持度低于阈值αα的前缀对应的项从数据集S删除,同时得到所有的频繁1项序列,i=1. 3)对于每个长度为i满足支持度要求的前缀进行递归挖掘: a) 找出前缀所对应的投影数据库。如果投影数据库为空,则递归返回。 b) 统计对应投影数据库中各项的支持度计数。如果所有项的支持度计数都低于阈值αα,则递归返回。 c) 将满足支持度计数的各个单项和当前的前缀进行合并,得到若干新的前缀。 d) 令i=i+1,前缀为合并单项后的各个前缀,分别递归执行第3步。 PrefixSpan算法小结 决策树简介 决策树类型 决策树构造过程 决策树学习采用自顶向下的分治方式构造判定树。决策树生成算法分成两个步骤:第一步是树的生成,开始时所有训练样本都在根节点,然后递归进行数据分片;第二步是树的修建。决策树停止分割的条件包括:一个节点上的数据都是属于同一个类别;没有属性可以再用于对数据进行分割。 预备知识:信息的定量描述 信息量的定义 根据客观事实和人们的习惯概念,函数f§应满足以下条件: 若一个消息x出现的概率为p,则这一消息所含的信息量为 信息熵 条件熵 平均互信息量 信息增益 高尔夫活动决策表 对于这个分类问题中,分类属性为“活动”,分类个数为2,分别为“进行”和取消两个类别。对于当前数据集合D,有9条元组属于分类“进行”,另外5条属于分类“取消”。为零对D中的元组进行分类,所需要的期望值定义为: 其中 p i p_{i} pi是D中任意元组属于分类 C i C_{i} Ci的概率,用 ∣ C i , D ∣ ∣ D ∣ \frac{|C_{i,D}|}{|D|} ∣D∣∣Ci,D∣来估计,即用D中属于各个分类的元组所占的比例来估计概率 p i p_{i} pi。Info(D)就是前面所介绍的信息熵,它是识别D中元组所属分类所需要的信息期望。在此例中: 为了构造决策树的根节点,先要选择一个属性作为分裂节点,使得D分裂后的信息量减少最多。下面分别计算按照某个属性A“分裂后”的信息熵: 假设属性A有v个离散的值,D中元组被划分为v个子集合 D j D_{j} Dj,计算得到 I n f o A ( D ) Info_{A}(D) InfoA(D)。 按照“天气”属性划分数据 “天气”属性有3个不同的值:{“晴”,“阴”,“雨”},划分后的3个子集合,在分类属性“活动上的纯度也不同,在“天气”取值为“阴”的这个子集合里,纯度最高,都为进行 I n f o 天 气 ( D ) = 5 14 ∗ I n f o ( D 晴 ) ) + 4 14 ∗ I n f o ( D 阴 ) ) + 5 14 ∗ I n f o ( D 雨 ) ) Info_{天气}(D)=\frac{5}{14}*Info(D_{晴}))+\frac{4}{14}*Info(D_{阴}))+\frac{5}{14}*Info(D_{雨})) Info天气(D)=145∗Info(D晴))+144∗Info(D阴))+145∗Info(D雨)) 可以看出,分裂后的数据集合D的信息熵明显减少,这说明分类所需要信息减少,这个减少的信息量,ID3算法称之为信息增益(偏向分支的的属性): G a i n ( A ) = I n f o ( D ) − I n f o A ( D ) Gain(A)=Info(D)-Info_{A}(D) Gain(A)=Info(D)−InfoA(D) 因为属性“天气”的信息增益最大,因此根节点选择“天气”属性。由于 D 晴 D_{晴} D晴和 D 雨 D_{雨} D雨的分类属性上不纯,两个分类标签都存在,因此需要进一步递归地进行分裂。 D晴按照属性“湿度”划分结果 D晴按照属性“风速”划分结果 对子集合 D 晴 D_{晴} D晴和 D 雨 D_{雨} D雨选择分类属性时,根据信息增益,分别选取了“湿度”和“风速”属性,可以发现,按照这两个属性分别划分后的子集合,纯度都很高。 先验熵:在没有接收到其它任何属性值时候,活动进行与否的熵。 H(活动) = - (9/14)*log (9/14) - (5/14)*log (5/14) = 0.94 增益率(Gain ratio) C4.5算法中采用Gain ratio代替Information gain 增益率: G a i n R a t e ( A ) = G a i n ( A ) S p l i t I n f o A ( D ) GainRate(A)=\frac{Gain(A)}{SplitInfo_{A}(D)} GainRate(A)=SplitInfoA(D)Gain(A) 选择具有最大信息增益率的属性划分数据集 C4.5算法:信息增益率 (Gain ratio) C4.5算法既可以处理离散型属性,也可以处理连续值属性。 Gain(income)=0.029 Gini系数: CART算法形成分类树步骤 欠拟合是指模型拟合程度不高,数据距离拟合曲线较远,或指模型没有很好地捕捉到数据特征,不能够很好地拟合数据。 为将所有训练样本分类,节点不断分裂,分支越来越多,这种过程很可能过分适应了训练数据集中的“噪声”,这种现象称为“过拟合”。 从图中可以看出,随着树的增长,决策树在训练集上的精度是单调上升的,在测试集上的精度呈先上升后下降的趋势。出现上述情况主要有如下原因: 预剪枝(pre-pruning) 后剪枝(post-pruning) 错误率降低剪枝(REP) REP将决策树上的每一个节点都作为修剪的候选对象,修建过程如下: [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pGr22Pqn-1616905728447)(https://img2020.cnblogs.com/blog/1971052/202102/1971052-20210227221925803-1031666788.png)] 从图中可观察到Node4本身关于剪枝集的误差为0,而它的子树Node8和Node9的误差之和为1>0,所以Node4应该被叶节点代替。 使用REP方法具有如下优点: 缺点: REP在数据量较少的情况下很少应用,因为REP偏向于过度修剪,在剪枝过程中,那些在剪枝集中不会出现的一些很稀少的训练数据实例所对应的分枝都要被删除。当剪枝集比训练集规模小很多的时候,这个问题更加突出。 信息增益: 偏向于多值属性,一个属性的信息增益越大,表明该属性的减少样本的熵的能力更强,这个属性使得数据由不确定性变成确定性的能力越强。所以,如果是取值更多的属性,更容易使得数据更“纯”(尤其是连续型数值),其信息增益更大,决策树会首先挑选出这个属性作为树的顶点。结果训练出来的形状是一颗庞大且深度很浅的树,遮掩的划分是极为不合适的。 增益率引入了分裂信息,取值数目多的属性分裂信息也会变大。将增益除以分裂信息,再加上一些额外操作,可以有效地解决信息增益过大地问题。增益率倾向于不平等地分裂,使得其中一个子集比其它子集要小得多。 倾向于多值属性,当类数目较大时,计算比较复杂,它倾向于大小相等地分区和纯度。 当K=4时,未知点会根据最近邻原理选取3个五角星,1个三角形,依据少数服从多数原理,将未知点归为五角星类别;当K=11时,未知点根据最近邻原理会选取5个五角星,6个三角形,此时未知点归属为三角形类别。 O ( n 3 ) O(n^{3}) O(n3) 距离的计算 优点: d树可以帮助我们在很快地找到与测试点最邻近的K个训练点。不再需要计算测试点和训练集中的每一个数据的距离。 kd树是二叉树的一种,是对k维空间的一种分割,不断地用垂直于坐标轴的超平面将k维空间切分,形成k维超矩形区域,kd树的每一个结点对应于一个k维超矩形区域。 kd树的构造 首先我们需要构造kd数,构造方法如下: 我们用图像来走算法! 我们有二维数据集 将他们在坐标系中表示如下: 开始:选择 x ( 1 ) x^{(1)} x(1)为坐标轴,中位数为6,即(6,5)为切分点,切分整个区域 以 x ( 2 ) x^{(2)} x(2)为坐标轴,选择中位数,可知左边区域为-3,右边区域为-12。所以左边区域切分点为(1,-3),右边区域切分点坐标为(17,-12) 再次对区域进行切分,同上步,我们可以得到切分点,切分结果如下: [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-V8D7LLBP-1616905728460)(https://img2020.cnblogs.com/blog/1971052/202102/1971052-20210228093445741-1829206295.png)] 最后分割的小区域内只剩下一个点或者没有点。我们得到最终的kd树如下图 kd树完成K近邻的搜索 当我们完成了kd树的构造之后,我们就要想怎么利用kd树完成K近邻的搜索呢??? 接下来,又是抛出算法的时候了 为了方便说明,我们采用二维数据的栗子。假设现在要寻找p点的K个近邻点(p点坐标为(a,b)),也就是离p点最近的K个点。设S是存放这K个点的一个容器。 新鲜的算法来了: (b)如果此时S中不足k个点,则将当前结点加入到S中;如果S中已有k个点,且当前结点与p点的距离小于S中最长距离,则用当前结点替换S中距离最远的点。 (c)计算p点和当前结点切分线的距离。如果该距离大于等于S中距离p最远的距离并且S中已有k个点,执行3;如果该距离小于S中最远的距离或S中没有k个点,从当前结点的另一子节点开始执行1;如果当前结点没有另一子结点,执行3。 以上的1,2,3我们会称为算法中的1,算法中的2,算法中的3 为了方便描述,我对结点进行了命名,如下图。 蓝色斜线表示该结点标记为已访问,红色下划线表示在此步确定的下一要访问的结点 我们现在就计算p(-1,-5)的3个邻近点。 我们拿着(-1,-5)寻找kd树的叶子结点。 执行算法中的1。 进行算法中的2,标记结点H已访问,将结点H加入到S中。 此时 执行算法中的3,当前结点H不是根结点 当前结点C不是根结点 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PUDnYq0O-1616905728475)(https://img2020.cnblogs.com/blog/1971052/202102/1971052-20210228094437830-1027464644.png)] 从结点D开始算法中的1 开始算法中的2 执行算法中的3,当前结点J不为根结点 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-s9lfidWY-1616905728478)(https://img2020.cnblogs.com/blog/1971052/202102/1971052-20210228094634167-2052136104.png)] 从结点I开始算法中的1,结点I已经是叶子结点 直接进行到算法中的2 执行算法中的3. 当前结点I不是根结点 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1q8PYoOa-1616905728480)(https://img2020.cnblogs.com/blog/1971052/202102/1971052-20210228095047024-277163094.png)] 执行算法中的3,发现当前结点A是根结点,结束算法。 得到p点的3个邻近点,为(-6,-5)、(1,-3)、(-2,-1) kd树就这么的完成了他的任务。 总的来说,就是以下几步 1、找到叶子结点,看能不能加入到S中 2、回退到父结点,看父结点能不能加入到S中 3、看目标点和回退到的父结点切分线的距离,判断另一子结点能不能加入到S中 Adaboost算法的基本流程: 总的来说,这个步骤有点像神经网络学习fp、bp的过程。 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cTS2mfPo-1616905728485)(https://img2020.cnblogs.com/blog/1971052/202103/1971052-20210325214141612-1269625114.png)] Adaboost的缺点 在Bagging中重点是随机采样,一般采用自助采样法(Bootstraping) Bootstraping(自助法)采样 Bagging和Boosting的各自特点 随机森林在bagging基础上做了修改。 特点 一文让你彻底理解准确率,精准率,召回率,真正率,假正率,ROC/AUC 以二分类为例,假设类别1为正,类别0为负,那么,对于数据测试结果有下面4种情况。 准确率(Accuracy): ( T P + T N ) ( T P + F P + T N + F N ) \frac{(TP+TN)}{(TP+FP+TN+FN)} (TP+FP+TN+FN)(TP+TN) 精确率(Precision): p = T P ( T P + F P ) p=\frac{TP}{(TP+FP)} p=(TP+FP)TP 召回率(Recall): r = T P ( T P + F N ) r = \frac{TP}{(TP+FN)} r=(TP+FN)TP F1分数(F1-score): F1-score= p ∗ r 2 ( p + r ) \frac{p*r}{2(p+r)} 2(p+r)p∗r 回归和分类区别 浅层: 两者的的预测目标变量类型不同,回归问题是连续变量,分类问题离散变量。 分类和聚类区别 分类和聚类的概念是比较容易混淆的。 对于分类来说,在对数据集分类时,我们是知道这个数据集是有多少种类的,比如对一个学校的在校大学生进行性别分类,我们会下意识很清楚知道分为“男”,“女” 而对于聚类来说,在对数据集操作时,我们是不知道该数据集包含多少类,我们要做的,是将数据集中相似的数据归纳在一起。比如预测某一学校的在校大学生的好朋友团体,我们不知道大学生和谁玩的好玩的不好,我们通过他们的相似度进行聚类,聚成n个团体,这就是聚类。 按照李春葆老师的话说,聚类是将数据对象的集合分成相似的对象类的过程。使得同一个簇(或类)中的对象之间具有较高的相似性,而不同簇中的对象具有较高的相异性。如下图所示 二、 聚类的定义 我们这样来对聚类进行定义。聚类可形式描述为:D={o1,o2,…,on}表示n个对象的集合,oi表示第i(i=1,2,…,n)个对象,Cx表示第x(x=1,2,…,k)个簇,CxÍD。用sim(oi,oj)表示对象oi与对象oj之间的相似度。若各簇Cx是刚性聚类结果,则各Cx需满足如下条件: 其中,条件①和②表示所有Cx是D的一个划分,条件③表示簇内任何对象的相似度均大于簇间任何对象的相似度。 聚类的整体流程如下: 三、聚类的方法 根据定义我们知道,聚类,简单的来说,是通过“臭味相投”的原理来进行选择“战友”的。 3.1距离相似度量 距离相似度度量是指样本间的距离越近,那么这俩样本间的相似度就越高。距离这个词我们可以这么理解,把数据集的每一个特征当做空间上的一个维度,这样就确定了两个点,这两个点间的“连接”直线就可以当做是它们的距离。一般有三种距离度量,曼哈顿距离、欧氏距离、闵可夫斯基距离,这三个距离表示方式都是原始距离的变形,具体形式如下: [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-esZFLyce-1616905728494)(https://img2020.cnblogs.com/blog/1971052/202103/1971052-20210325215842825-118491519.png)] 因为相似度与距离是反比的关系,因此在确定好距离后可以设计相似函数如下: 其中,K-means算法就是基于距离的聚类算法 3.2密度相似度度量 密度相似度的出发点是 “物以类聚,人以群分”,相同类别的物体往往会“抱团取暖”,也就是说,每个团体都会围在一个圈子里,这个圈子呢,密度会很大,所以就有密度相似度度量这一考察形式。 density(Ci,Cj)=|di-dj| 其中di、dj表示簇Ci、Cj的密度。其值越小,表示密度越相近,Ci、Cj相似性越高。这样情况下,簇是对象的稠密区域,被低密度的区域环绕。 其中,DBSCAN就是基于密度的聚类算法 3.3连通性相似度度量 数据集用图表示,图中结点是对象,而边代表对象之间的联系,这种情况下可以使用连通性相似性,将簇定义为图的连通分支,即图中互相连通但不与组外对象连通的对象组。 也就是说,在同一连通分支中的对象之间的相似性度量大于不同连通分支之间对象的相似性度量。 3.4概念相似度度量 若聚类方法是基于对象具有的概念,则需要采用概念相似性度量,共同性质(比如最近邻)越多的对象越相似。簇定义为有某种共同性质的对象的集合。 四、聚类的评定标准 说了这么多聚类算法,我们都知道,聚类算法没有好坏,但聚类之后的结果根据数据集等环境不同有着好坏之分,那么该怎么评价聚类的好坏呢? 一个好的聚类算法产生高质量的簇,即高的簇内相似度和低的簇间相似度。通常估聚类结果质量的准则有内部质量评价准则和外部质量评价准则。比如,我们可以用CH指标来进行评定。CH指标定义如下: 其中: traceB表示簇间距离,traceW表示簇内距离,CH值越大,则聚类效果越好。 逻辑回归主要解决二分类问题 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YvDKEfvU-1616905728505)(https://img2020.cnblogs.com/blog/1971052/202103/1971052-20210327164639903-1345710810.png)] [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aXDQis4s-1616905728508)(https://img2020.cnblogs.com/blog/1971052/202103/1971052-20210325220943882-568858032.png)] 第一种方法容易收到随机取值的影响 轮廓系数法 追求内部聚类最小化,外部距离最大化 k-means算法小结 优点: N为样本点个数,K为中心点个数,I为迭代次数 缺点: Canopy算法的优缺点 优点: 缺点: 1.算法中T1、T2的确定问题,依旧可能落入局部最优解 分母A是当前点到所有点距离的平方和,分子是当前点到距离点的平方,这个算法的方法就是比如选取2作为质心,下一个就选取离2最远的15作为质心 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2kEGiRv7-1616905728516)(https://img2020.cnblogs.com/blog/1971052/202103/1971052-20210327195620502-1513124162.png)] 实现流程: ●1.所有点作为一个簇 例如将下列簇分成五个簇 隐含的一个原则 因为聚类的误差平方和能够衡量聚类性能,该值越小表示数据单越接近于他们的质心,聚类效果就越好。所以需要对误差平方和最大的簇进行再一次划分, 因为误差平方和越大,表示该簇聚类效果越不好,越有可能是多个簇被当成了一个簇,所以我们首先需要对这个簇进行划分。 二分K均值算法可以加速K-means算法的执行速度,因为它的相似度计算少了并且不受初始化问题的影响,因为这里不存在随机点的选取,且每一步都保证了误差最小. K-medoids和K-means是有区别的,不一样的地方在于中心点的选取 算法流程: (1)总体n个样本点中任意选取k个点作为medoids k-medoids对噪声鲁棒性好。 例:当一个cluster样本点只有少数几个,如(1,1) (1,2) (2,1) (1000,1000) 。其中(1000,1000) 是噪声。如果按照k-means质心大致会处在(1,1) (1000,1000) 中间即((1+1000)/2,(1+1000)/2),这显然不是我们想要的。这时k-medoids就可以避免这种情况,他会在(1,1) (1,2) (2,1) (1000,1000) 中选出一个样本点使cluster的绝对误差最小,计算可知一定会在前三个点中选取。 适合大数据的聚类算法 该算法的迭代步骤有两步: 与Kmeans相比,数据的更新在每一个小的样本集上。 对于每一个小批量,通过计算平均值得到更新质心,并把小批量里的数据分配给该质心,随着迭代次数的增加,这些质心的变化是逐渐减小的,直到质心稳定或者达到指定的迭代次数,停止计算。 基本概念: ( Density-Based Spatial Clustering of Applications with Noise ) 半径值和阈值需要自己设置,不需要设置k值 直接密度可达:若某点p在点q的r邻域内,且q是核心点则p-q直接密度可达。 DBSCAN算法优点: DBSCAN算法缺点: DBSCAN算法使用中有以下两个问题: 初始参数领域半径(ε)和领域最小点数(Minpts)需要手动设置,并且聚类的质量十分依赖这两个参数的取值 OPTICS主要概念: 核心距离 核心距离是一个点成为核心点的最小领域半径 可达距离 DBSCAN中有三个连接各密集区域的重要概念:直接密度可达、密度可达、密度相连 KNN算法和kd树详解(例子+图示) 浅谈机器学习-回归与分类的区别 分类聚类区别及聚类概述
序列是元素e1,e2,···,en构成的有序串,记为GSP算法
Sequential patterns with length 3
After join
After Pruning
<(1,2)3>
<(1,2)(3,4)>
<(1,2)(3,4)>
<(1,2)4>
<(1,2) 3 5>
<1(3,4)>
<(1,3)5>
<2(3,4)>
<2 3 5>
Freespan算法
(1)第1遍扫描S,构造频繁项矩阵;
(2)生成长度为2的序列模式,循环项模式的标记和投影数据库的标记;
(3)再次扫描S,生成循环项模式和投影数据;
(4)对生成的投影数据库递归调用矩阵投影挖掘算法挖掘更长的候选模式。
它将频繁序列和频繁模式的挖掘统一起来,把挖掘工作限制在投影数据库中,还能限制序列分片的增长。它能有效地发现完整地序列模式,同时大大减少产生候选序列所需地开销,比基于Apriori的GSP算法快很多。
它可能会产生许多投影数据库,如果一个模式在数据库中的每个序列中出现,该模式的投影数据库将不会缩减;另外,一个长度为k的序列可能在任何位置增长,那么长度为k+1的候选序列必须对每个可能的组合情况进行考察,这样所需的开销是比较大的。PrefixSpan算法
PrefixSpan算法的全称是Prefix-Projected Pattern Growth,即前缀投影的模式挖掘。里面有前缀和投影两个词。那么我们首先看看什么是PrefixSpan算法中的前缀prefix。
前缀
后缀(前缀投影)
< a >
<(abc)(ac)d(cf)>
< aa >
<(_bc)(ac)d(cf)>
< a(ab) >
<(_c)(ac)d)cf>
现在我们来看看PrefixSpan算法的思想,PrefixSpan算法的目标是挖掘出满足最小支持度的频繁序列。那么怎么去挖掘出所有满足要求的频繁序列呢。回忆Aprior算法,它是从频繁1项集出发,一步步的挖掘2项集,直到最大的K项集。PrefixSpan算法也类似,它从长度为1的前缀开始挖掘序列模式,搜索对应的投影数据库得到长度为1的前缀对应的频繁序列,然后递归的挖掘长度为2的前缀所对应的频繁序列····以此类推,一直递归到不能挖掘到更长的前缀挖掘为止。
输入:序列数据集S和支持度阈值αα
第四章 分类与回归算法
数据分类主要包含两个步骤:第一步,事先利用已有数据样本建立一个数学模型,这一步通常称为“训练”,为建立模型的学习过程提供的具有类标号的数据称为“训练集”;第二步,使用模型,对未知分类的对象进行分类。
决策树算法
决策树分为分类树和回归树两种,分类树相对离散变量做决策树,回归树则对连续变量做决策树。
根据决策树的不同属性,可将其分为以下几种。
例:在一个口袋中,有100个球,其中1个是红球,另外99个是绿球,现在你随意抓一个球。
如果事先预言家告诉你将抓到绿球,你会觉得惊讶吗?
如果预言家告诉你将抓到红球,则觉得他的确有神算能力。
f§应是概率p的严格单调递减函数,即当p1>p2, f(p1)
当p=0时,f§=∞;
两个独立事件的联合信息量应等于它们分别的信息量之和。
I ( X i ) = − l o g P ( X i ) I(X_{i})=-logP(X_{i}) I(Xi)=−logP(Xi) 单位:bit
例:
抛一枚均匀硬币,出现正面与反面的信息量是多少?
I(正)= I(反)= − l o g 2 -log_{2} −log2 0.5=1b
抛一枚畸形硬币,出现正面与反面的概率分别是1/4,3/4,出现正面与反面时的信息量是多少?
I(正)= − l o g 2 -log_{2} −log2 1/4=2b;I(反)= − l o g 2 -log_{2} −log2 3/4=0.415b
信源含有的信息量是信源发出的所有可能消息的平均不确定性
信息论创始人香农把信源所含有的信息量称为信息熵(entropy),是指每个符号所含信息量的统计平均值。m种符号的平均信息量为:
H ( X ) = − ∑ i = 1 n p ( X i ) I ( X i ) = − ∑ i = 1 n p ( X i ) l o g p ( X i ) H(X)=-\sum_{i=1}^{n}p(X_{i})I(X_{i})=-\sum_{i=1}^{n}p(X_{i})logp(X_{i}) H(X)=−i=1∑np(Xi)I(Xi)=−i=1∑np(Xi)logp(Xi)
抛一枚均匀硬币的信息熵是多少?
()=−(0.50.5+0.50.5)=1
抛一枚畸形硬币,出现正面与反面的概率分别是1/4,3/4,出现正面与反面时的信息熵是多少?
()=−(1/4 1/4+3/4 3/4)=0.811
如果信源X与随机变量Y不是互相独立的,收信者接收到信息Y。那么,用条件熵H(X|Y)来度量收信者再收到随机变量Y之后,随机变量X仍然存在的不确定性。设X对应信源符号Xi,Y对应信源符号Yj,P(Xi|Yj)为当Y为Yj时,X为Xi的概率,则有:
H ( X ∣ Y ) = − ∑ i = 1 n ∑ j = 1 n P ( X i ∣ Y j ) l o g P ( X i ∣ Y j ) H(X|Y)=-\sum_{i=1}^{n}\sum_{j=1}^{n}P(X_{i}|Y_{j})logP(X_{i}|Y_{j}) H(X∣Y)=−i=1∑nj=1∑nP(Xi∣Yj)logP(Xi∣Yj)
用它来表示信号Y所能提供的关于X的信息量的大小,用I(X,Y)表示:
I(X|Y)=H(X)-H(X|Y)
D在属性A上“分裂后”,标识各个元组所需信息量减少多少,用信息增益(Information Gain)来表示:
Gain(A) = Info(D) - InfoA(D)
Info(D)就是前面所介绍的信息熵
ID3算法选择信息增益最大的属性作为当前的“分裂属性”。(这样做的考虑是什么?)
这样做使得目前要完成最终分类所需的信息量最小ID3算法
(信息熵越大越不确定)
编号
天气
温度
湿度
风速
活动
1
晴
炎热
高
弱
取消
2
晴
炎热
高
强
取消
3
阴
炎热
高
弱
进行
4
雨
适中
高
弱
进行
5
雨
寒冷
正常
弱
进行
6
雨
寒冷
正常
强
取消
7
阴
寒冷
正常
强
进行
8
晴
适中
高
弱
取消
9
晴
寒冷
正常
弱
进行
10
雨
适中
正常
弱
进行
11
晴
适中
正常
强
进行
12
阴
适中
高
强
进行
13
阴
炎热
正常
弱
进行
14
雨
适中
高
强
取消
I n f o ( D ) = − ∑ i = 1 m p i l o g 2 ( p i ) Info(D)=-\sum_{i=1}^{m}p_{i}log_{2}(p_{i}) Info(D)=−i=1∑mpilog2(pi)
I n f o ( D ) = − 9 14 l o g 2 ( 9 14 ) − 5 14 l o g 2 ( 5 14 ) = 0.940 ( b i t ) Info(D)=-\frac{9}{14}log_{2}(\frac{9}{14})-\frac{5}{14}log_{2}(\frac{5}{14})=0.940(bit) Info(D)=−149log2(149)−145log2(145)=0.940(bit)
I n f o ( D ) = ∑ j = 1 v ∣ D j ∣ ∣ D ∣ ∗ I n f o ( D j ) Info(D)=\sum_{j=1}^{v}\frac{|D_{j}|}{|D|}*Info(D_{j}) Info(D)=j=1∑v∣D∣∣Dj∣∗Info(Dj)
先以属性“天气”为例
编号
天气
温度
湿度
风速
活动
9
晴
寒冷
正常
弱
进行
11
晴
适中
正常
强
进行
1
晴
炎热
高
弱
取消
2
晴
炎热
高
强
取消
8
晴
适中
高
弱
取消
3
阴
炎热
高
弱
进行
7
阴
寒冷
正常
强
进行
12
阴
适中
高
强
进行
13
阴
炎热
正常
弱
进行
4
雨
适中
高
弱
进行
5
雨
寒冷
正常
弱
进行
10
雨
适中
正常
弱
进行
6
雨
寒冷
正常
强
取消
14
雨
适中
高
强
取消
I n f o ( D 晴 ) = − 2 5 l o g 2 ( 2 5 ) − 3 5 l o g 2 ( 3 5 ) = 0.971 Info(D_{晴})=-\frac{2}{5}log_{2}(\frac{2}{5})-\frac{3}{5}log_{2}(\frac{3}{5})=0.971 Info(D晴)=−52log2(52)−53log2(53)=0.971
I n f o ( D 阴 ) = − 4 4 l o g 2 ( 4 4 ) = 0 Info(D_{阴})=-\frac{4}{4}log_{2}(\frac{4}{4})=0 Info(D阴)=−44log2(44)=0
I n f o ( D 雨 ) = − 2 5 l o g 2 ( 2 5 ) − 3 5 l o g 2 ( 3 5 ) = 0.971 Info(D_{雨})=-\frac{2}{5}log_{2}(\frac{2}{5})-\frac{3}{5}log_{2}(\frac{3}{5})=0.971 Info(D雨)=−52log2(52)−53log2(53)=0.971
I n f o 天 气 ( D ) = 5 14 ∗ 0.971 + 4 14 ∗ 0 + 5 14 ∗ 0.971 = 0.694 Info_{天气}(D)=\frac{5}{14}*0.971+\frac{4}{14}*0+\frac{5}{14}*0.971=0.694 Info天气(D)=145∗0.971+144∗0+145∗0.971=0.694
信息增益选择大的,但并不是信息增益越大在决策树中最有益
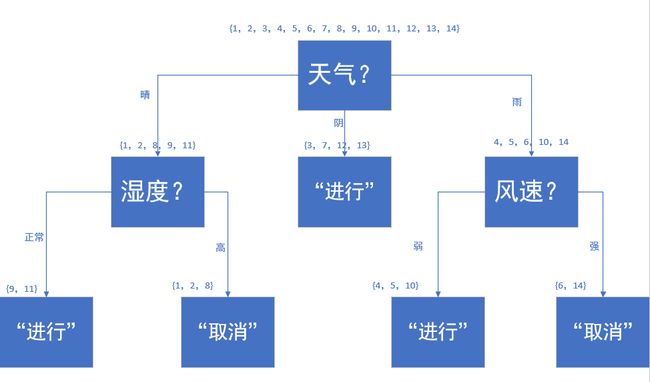
G a i n ( 天 气 ) = 0.940 − 0.694 = 0.246 Gain(天气)=0.940-0.694=0.246 Gain(天气)=0.940−0.694=0.246
G a i n ( 温 度 ) = 0.940 − 0.911 = 0.029 Gain(温度)=0.940-0.911=0.029 Gain(温度)=0.940−0.911=0.029
G a i n ( 湿 度 ) = 0.940 − 0.789 = 0.151 Gain(湿度)=0.940-0.789=0.151 Gain(湿度)=0.940−0.789=0.151
G a i n ( 风 速 ) = 0.940 − 0.892 = 0.048 Gain(风速)=0.940-0.892=0.048 Gain(风速)=0.940−0.892=0.048
编号
天气
温度
湿度
风速
活动
9
晴
寒冷
正常
弱
进行
11
晴
适中
正常
强
进行
1
晴
炎热
高
弱
取消
2
晴
炎热
高
强
取消
8
晴
适中
高
弱
取消
编号
天气
温度
湿度
风速
活动
4
雨
适中
高
弱
进行
5
雨
寒冷
正常
弱
进行
10
雨
适中
正常
弱
进行
6
雨
寒冷
正常
强
取消
14
雨
适中
高
强
取消
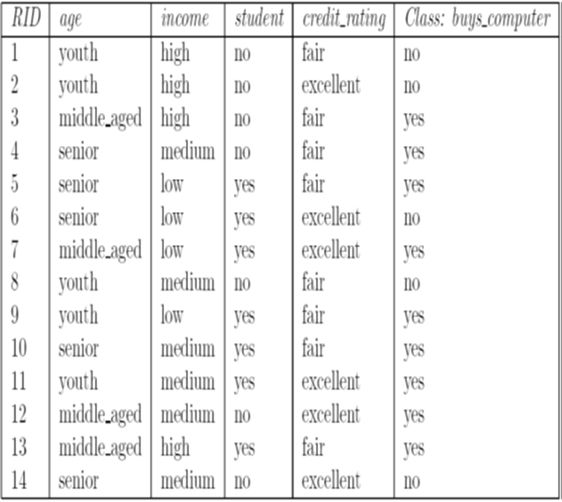
决策树形成过程:信息论在ID3算法中的应用
H(活动|晴天)=−P(进行|晴天)logP(进行|晴天)−P(取消|晴天)logP(取消|晴天)=- (2/5)*log2(2/5) - (3/5)*log2(3/5) = 0.971
H(活动|阴天)=−P(进行|阴天)logP(进行|阴天)−P(取消|阴天)logP(取消|阴天)=- (4/4)*log2(4/4) = 0
H(活动|雨天)=−P(进行|雨天)logP(进行|雨天)−P(取消|雨天)logP(取消|雨天) = - (3/5)*log2(3/5)- (2/5)*log2(2/5) =0.971
则条件熵如下:
H(活动|天气)=5/14∗H(活动|晴天)+4/14∗H(活动|阴天)+5/14∗H(活动|雨天)= (5/14)*0.971 + (4/14)*0 +(5/14)*0.971=0.693
恰好就是 I n f o 天 气 ( D ) Info_{天气}(D) Info天气(D),所以得出结论,信息增益就是平均互信息量:
H(活动,天气)=H(活动)-H(活动|天气)=0.94-0.694=0.246
可以看出,选择测试属性A对于分类提供的信息越大,选择A之后对分类的不确定程度就越小。不确定程度的减少量就是信息的增益。C4.5算法
引入分裂信息,代表按照属性A分裂样本D的广度和均匀性:
S p l i t I n f o A ( D ) = − ∑ j = 1 n D j D ∗ l o g 2 ( D j D ) SplitInfo_{A}(D)=-\sum_{j=1}^{n}\frac{D_{j}}{D}*log_{2}(\frac{D_{j}}{D}) SplitInfoA(D)=−j=1∑nDDj∗log2(DDj)
gain_ratio(income) = 0.029/1.557 = 0.019CART算法
CART算法采用最小Gini系数选择内部节点的分裂属性。
G i n i ( D ) = 1 − ∑ i = 1 m p i 2 Gini(D)=1-\sum_{i=1}^{m}p_{i}^{2} Gini(D)=1−i=1∑mpi2
G i n i A ( D ) = ∣ D 1 ∣ ∣ D ∣ G i n i ( D 1 ) + ∣ D 2 ∣ ∣ D ∣ G i n i ( D 2 ) Gini_{A}(D)=\frac{|D_{1}|}{|D|}Gini(D_{1})+\frac{|D_{2}|}{|D|}Gini(D_{2}) GiniA(D)=∣D∣∣D1∣Gini(D1)+∣D∣∣D2∣Gini(D2)
CART算法选择具有最小 G i n i A ( D ) Gini_{A}(D) GiniA(D)的属性(不纯度减少最大) 用于分裂节点 (需要枚举所有可能的分裂情况)
1. 划分点:“晴”,划分后的子集合:{晴},{阴,雨};
2. 划分点:“阴”,划分后的子集合:{阴},{晴,雨};
3. 划分点:“雨”,划分后的子集合:{雨},{晴,阴}。
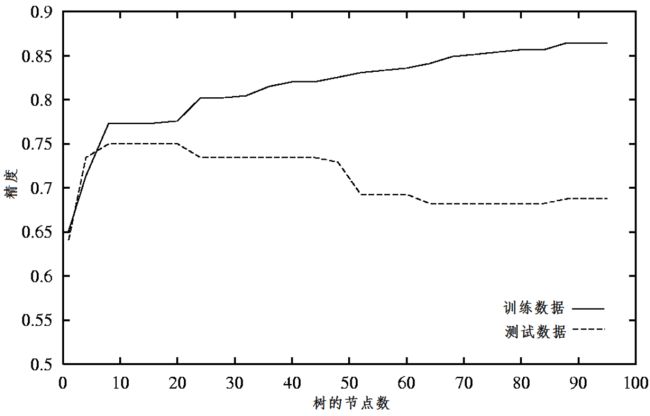
例子:过拟合与决策树剪枝
精度是精确性的度量,表示被分为正例的示例中实际为正例的比例,precision=TP/(TP+FP)
1. 定义一个高度,当决策树的高度达到此值时,即停止决策树的生长;
2. 定义一个阈值,当到达某节点的样本个数小于该值时,停止树的生长;
3. 定义一个阈值,如当前分支对性能增益小于该值时,停止树生长;
1. 很难精确地估计何时停止决策树的生长;
2. 预剪枝存在视野效果问题,也就是说可能当前的扩展会造成过渡拟合训练数据,但更进一步的扩展能够满足要求,也有可能准确地拟合训练数据。这将使得算法过早地停止决策树的构造。
构造完整的决策树,允许过度拟合训练数据;然后,对那些置信度不够的节点子树用叶节点代替。该叶子的类标号设为子树根节点所对应的子集中战术类别最多的类别。
后剪枝方法主要有以下几个方法:
1. 删除以此结点为根的子树
2. 使其成为叶子结点
3. 赋予该结点关联的训练数据的最常见分类
4. 当修剪后的树对于验证集合的性能不会比原来的树差时,才真正删除该结点
几种属性选择度量的对比
增益率:
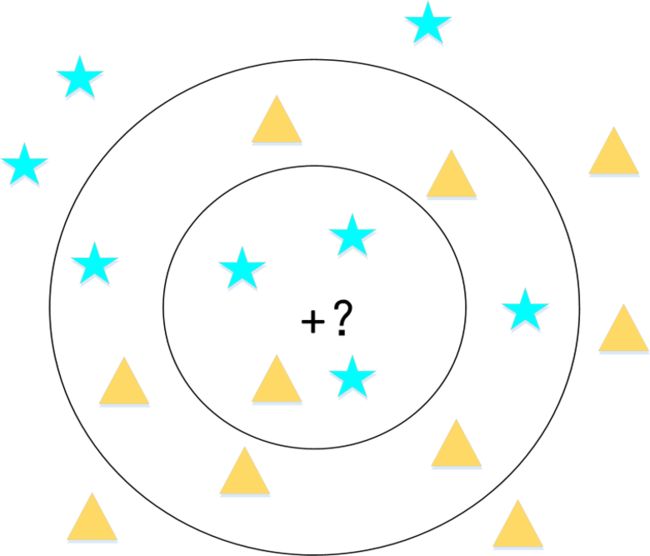
Gini系数:K最近邻(KNN)算法原理
K值过大时,意味着最后选取的参考样本点数量较大,极限的情况则是考虑所有的样本,此时就会存在一个明显的问题,当训练样本集不平衡时,此时占数多的类别更占优势。所以较大的K值能够减小噪声的影响,但会使类别之间的界限变得模糊;但K值过小时,极限来看便是取最近的样本点,这样的学习缺少了泛化能力,同时很容易受噪声数据和异常值的影响。因此,K值的设定在KNN算法中十分关键,取值过大易造成欠拟合效果,取值过小易造成过拟合效果。常见的确定K值的方法有:
取训练集中样本总数的平方根。
根据验证集,通过交叉验证确定K值。
KNN算法基本过程如下:
每个样本由n个数值型属性构成
两个样本间的距离用“欧氏距离”表示:
D ( X , Y ) = ∑ i = 1 n ( x i − y i ) 2 D(X,Y)=\sqrt{\sum_{i=1}^{n}(x_{i}-y_{i})^{2}} D(X,Y)=∑i=1n(xi−yi)2
D(John, Rachel)=sqrt [(35-41)2+(95K-215K)2 +(3-2)2]
不足:
![]()
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ApcsyzMx-1616905728453)(https://img2020.cnblogs.com/blog/1971052/202102/1971052-20210228093203226-1433312525.png)]
(a)回退到当前结点的父结点,此时的结点为当前结点(回退之后的结点)。将当前结点标记为已访问,执行(b)和(c);如果当前结点已经被访过,再次执行(a)。
![]()
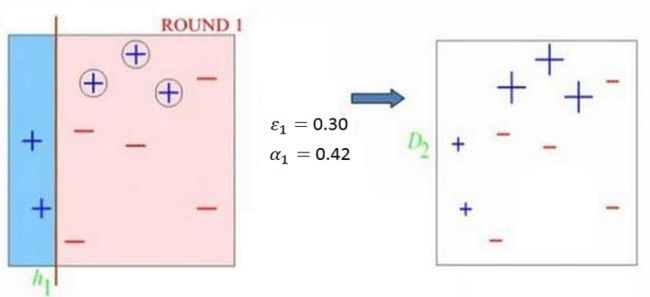
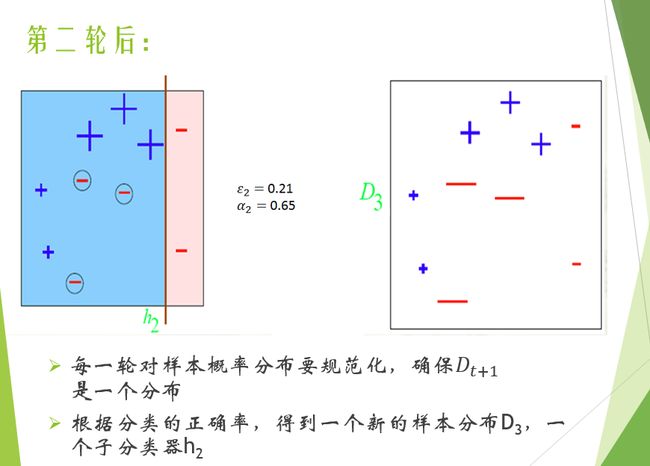
Adaboost算法
重复步骤2,3直至当前集成学习器的预测误差为0或达到分类器规定阈值。
Bagging算法
Bagging是与Boosting算法思想相对的集成算法,它包括以下主要思想。
来自成语“pull up by your own bootstraps”,意思是依靠自己的力量,称为自助法;
它是一种有放回的抽样方法。
Boosting注重对真实结果的逼近拟合,侧重偏差。降低偏差的方法是不断地修正预测结果和真是结果间的距离。
Bagging还注重在多个数据集/多种环境下的训练,侧重方差。降低方差的方法就是利用相互交叉的训练集让每个学习器都得到充分的训练。
Bagging的训练速度较Boosting更快,其性能依赖于基分类器的稳定性。如果基分类器不稳定,那么Bagging有助于降低训练数据的随机波动导致的误差;如果基分类器稳定,那么集成分类器的误差主要有基分类器的偏倚引起。随机森林
分类器算法的评估
回归分析
回归会给出一个具体的结果,例如房价的数据,根据位置、周边、配套等等这些维度,给出一个房价的预测。
分类相信大家都不会陌生,生活中会见到很多的应用,比如垃圾邮件识别、信用卡发放等等,就是基于数据集,作出二分类或者多分类的选择。
中层: 回归问题是定量问题,分类问题是定性问题。
高层: 回归与分类的根本区别在于输出空间是否为一个度量空间。
那么这个“臭味相投”的原理或准则是什么呢?
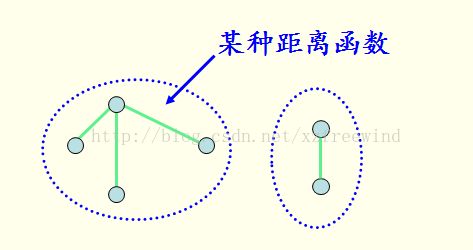
前人想出了四种相似度的比对方法,即距离相似度度量、密度相似度度量、连通性相似度度量和概念相似度度量。
密度是单位区域内的对象个数。密度相似性度量定义为:![]()
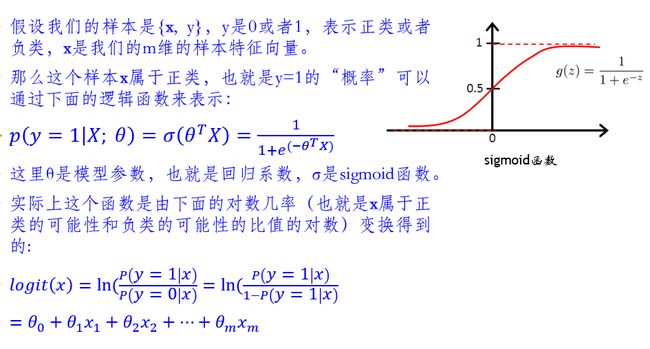
逻辑回归
逻辑回归的输入就是线性回归的输出第五章 聚类算法
k-means(k均值)
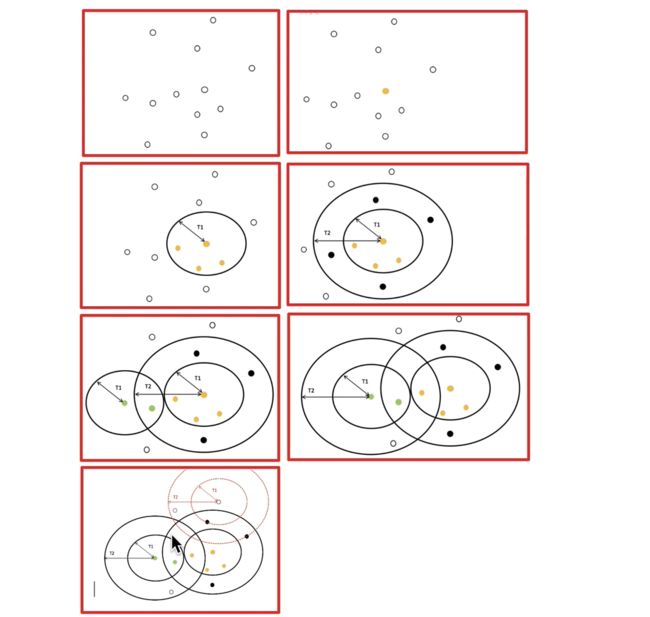
Canopy算法配合初始聚类
k-means++
二分k-means
●2.将该簇一分为二
●3.选择能最大限度降低聚类代价函数(也就是误差平方和)的簇划分为两个簇。
●4.以此进行下去,直到簇的数目等于用户给定的数目k为止(或误差平方和达到阈值)。K-medoids(k-中心聚类算法)
● K-means中, 将中心点取为当前cluster中所有数据点的平均值,对异常点很敏感!
● K-medoids中, 将从当前cluster中选取到其他所有(当 前cluster中的)点的距离之和最小的点作为中心
(2)按照与medoids最近的原则,将剩余的n-k个点分配到当前最佳的medoids代表的类中
(3)对于第i个类中除对应medoids点外的所有其他点,按顺序计算当其为新的medoids时,代价函数的值,遍历所有可能,选取代价函数最小时对应的点作为新的medoids
(4)重复2-3的过程,直到所有的medoids点不再发生变化或已达到设定的最大迭代次数
(5)产出最终确定的k个类
k-medoids只能对小样本起作用,样本大,速度就太慢了,当样本多的时候,少数几个噪音对k-means的质心影响也没有想象中的那么重,所以k-means的应用明显比k-medoids多。Mini Batch K-Means(小批量k均值算法)
大数据量是什么量级?通常当样本量大于1万做聚类时,就需要考虑选用Mini Batch K-Means算法。
Mini Batch KMeans使用了Mini Batch (分批处理)的方法对数据点之间的距离进行计算。
Mini Batch计算过程中不必使用所有的数据样本,而是从不同类别的样本中抽取一部分样本来代表各自类型进行计算。由于计算样本量少,所以会相应的减少运行时间,但另一方面抽样也必然会带来准确度的下降。
(1)从数据集中随机抽取一些数据形成小批量,把他们分配给最近的质心
(2)更新质心DBSCAN算法
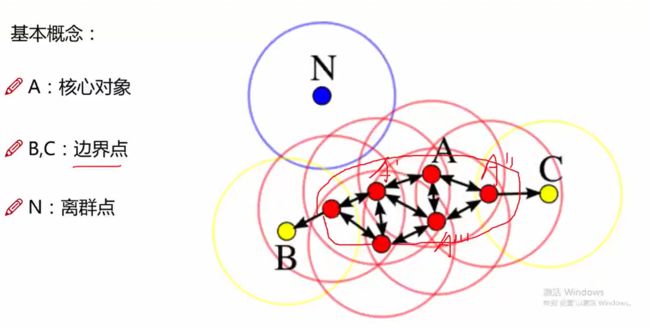
核心对象:若某个点的密度达到算法设定的阈值则其为核心点。(即r邻域内点的数量不小于minPts ,例如设置当在一个范围内点数大于3个的为核心对象)
ϵ \epsilon ϵ-邻域的距离阈值:设定的半径r
ϵ \epsilon ϵ小 M大 多噪声
ϵ \epsilon ϵ小 M小 高密度簇
ϵ \epsilon ϵ大 M小 簇小
密度可达:若有一个点的序列q0、q1、··· qk ,对任意qi-qi-1是直接密度可达的,则称从q0到qk密度可达,这实际上是直接密度可达的"传播"。
密度相连:若xi与xj均由xk密度可达,则称xi和xj密度相连,密度相连是对称关系
边界点:属于某一个类的非核心点,不能发展下线了
噪声点:不属于任何一个类簇的点,从任何一一个核心点出发都是密度不可达的
OPTICS算法
由于算法针对全局密度,当数据集的密度变化较大时,可能识别不出某些簇
针对以上问题,OPTICS进行了完善,在密度高低配置上,OPTICS算法增加了两个新的概念以降低聚类结果对初始参数的敏感度。且OPTICS算法并不显式的产生数据集聚类,而是输出一个以样本点输出次序为横轴,以可达距离为纵轴的图。这个排序代表了各样本点基于密度的聚类结构,从中可以得到基于任何半径和阈值的聚类。参考博文