【机器学习】吴恩达作业8.0，python实现异常检测

8.0.异常检测

实现异常检测算法，并将其应用于检测网络中的故障服务器。在第二部分中，您将使用协同过滤来构建电影推荐系统。
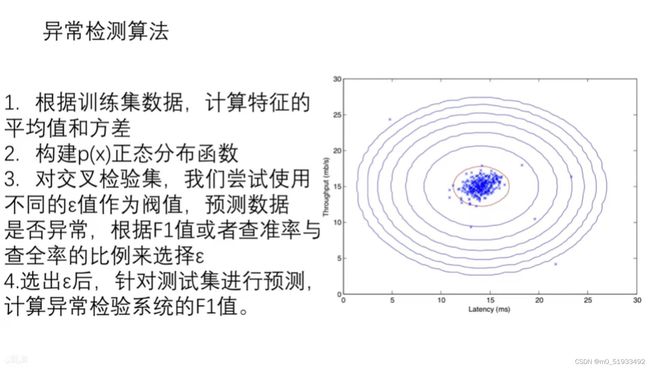
在本练习中，您将实现一个异常检测算法来检测服务器计算机中的异常行为。这些特性度量每个服务器的吞吐量(mb/s)和响应的延迟(ms)。在服务器运行时，您收集了m = 307个关于它们行为的样本，因此有一个未标记的数据集{x(1)，…，x(m)}。您怀疑这些样本中的绝大多数都是正常运行的服务器的“正常”(非异常)样本，但是也可能有一些服务器在这个数据集中异常运行的样本。
您将使用高斯模型来检测数据集中的异常样本。您将首先从一个二维数据集开始，该数据集可以可视化算法在做什么。在该数据集上，您将拟合高斯分布，然后找到概率非常低的值，考虑为异常。之后，您将把异常检测算法应用于多维的较大数据集。

异常检测（anomaly detection）：

异常检测就是发现与大部分对象不同的对象，其实就是发现离群点。异常检测有时也称偏差检测。异常对象是相对罕见的。用数据集建立概率模型p ( x )，如果新的测试数据在这个模型上小于某个阈值，则说它极大可能为异常点

常见的异常检测的应用：

• 欺诈检测：主要通过检测异常行为来检测是否为盗刷他人信用卡。
• 入侵检测：检测入侵计算机系统的行为
• 医疗领域：检测人的健康是否异常

 

 步骤：

1 求均值和方差

2 计算正态分布密度函数

密度估计（density estimation）使用联合密度函数作为概率模型

3 求阈值

F1的选择基于查准率（Precision)，查全率（recall，在验证集上尝试不同的阈值，选择能最大化F1值的阈值

 

 

选择异常检验/监督学习：

1.选择异常检验
反例数量远远大于正例数量时（正例数量过少）
异常的情况有多种不同的可能性时
2.选择监督学习
正反例数量相当时（正例数量足够）
未来的反例和训练集中的很类似

多元高斯分布 ：特征相关的情况下使用多元高斯分布

原始模型（一元高斯的乘积）：当特征之间存在线性关系时，想通过异常的组合值来捕捉异常样本，必须人工创造新特征捕捉异常。

计算简单，且较好适应m(训练集数量)小的情况。

多元高斯模型：自动捕捉特征之间的线性相关（协方差）。

计算较复杂，必须满足m>n(特征数量)，否则协方差矩阵不可逆。且特征间无线性相关。

 python语法

1 numpy.diag()函数   

是以一维数组的形式返回方阵的对角线（或非对角线）元素，或将一维数组转换成方阵（非对角线元素为0）

2  np.linalg.det 绝对值

3  np.linalg.inv取逆,      .T矩阵转置

4  np.ndim返回的是数组的维度，返回的只有一个数，该数即表示数组的维度。

代码 ：

1 导入数据可视化

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio
data = sio.loadmat('ex8data1.mat')
data.keys()#dict_keys(['__header__', '__version__', '__globals__', 'X', 'Xval', 'yval'])

X,Xval,yval = data['X'],data['Xval'],data['yval']
X.shape,Xval.shape,yval.shape #((307, 2), (307, 2), (307, 1))

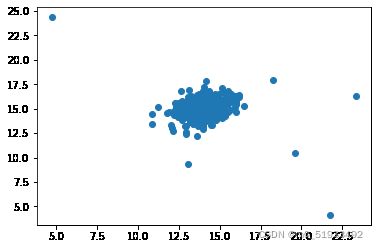
plt.scatter(X[:,0],X[:,1])
plt.show

 2 获取均值和方差

#1.获取训练集中样本特征的均值和方差
def estumateGaussian(X,isCovariance):
    means = np.mean(X,axis = 0)
    if isCovariance:#特征之间有线性关系
        sigma = (X - means).T@(X-means)/len(X)
    else:
        sigma = np.var(X,axis = 0)#特征之间没有线性关系
    return means,sigma

means,sigma = estumateGaussian(X,isCovariance = True)
sigma #array([[ 1.83263141, -0.22712233],
       [-0.22712233,  1.70974533]])

means,sigma = estumateGaussian(X,isCovariance = False)
sigma#array([1.83263141, 1.70974533])

3 求密度函数 

# 2.多元正态分布密度函数p

def gaussian(X, means, sigma):
    p = np.zeros((X.shape[0],1))#(307,1)
    n = len(means)
    if np.ndim(sigma) == 1:#返回sigma的维度是1
        sigma = np.diag(sigma) #将一维数组转化为方阵，非对角线元素为0
    for i in range(X.shape[0]):#遍历每一行，计算每一行的多元正态分布密度函数
        p[i] = (2*np.pi)**(-n/2) * np.linalg.det(sigma)**(-1/2) * np.exp(-0.5*(X[i,:]-means)[email protected](sigma)@(X[i,:]-means))
        #.T矩阵转置   mp.linalg.inv 矩阵求逆
    return p

p1 = gaussian(X,means,sigma)
p1.shape#(307, 1)

4 绘制密度函数等高线 

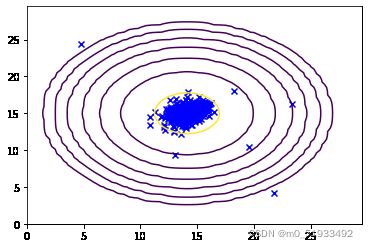
# # #3.绘图
def plotGaussian(X,means,sigma):
    x = np.arange(0,30,0.5)
    y = np.arange(0,30,0.5)
    xx,yy = np.meshgrid(x,y)
    z =  gaussian(np.c_[xx.ravel(),yy.ravel()],means,sigma)#计算对应的高斯分布函数
    zz = z.reshape(xx.shape)
    contour_levels = [10**h for h in range(-20,0,3)]
    plt.contour(xx,yy,zz,contour_levels)
    plt.scatter(X[:,0],X[:,1],marker='x', c='b')
    plt.show

means,sigma = estumateGaussian(X,isCovariance = False)
plotGaussian(X,means,sigma)

5 取最佳 

#4.阈值epsilonz自取
def selecteps(yval,p):
    bestEpsilon = 0
    bestF1 = 0
    epsilons = np.linspace(min(p),max(p),1000)
    for e in epsilons:
        p_ = p < e
        tp = np.sum((yval ==1)&(p_ == 1))
        fp = np.sum((yval ==0)&(p_ == 1))
        tn = np.sum((yval ==0)&(p_ == 0))
        fn = np.sum((yval ==1)&(p_ == 0))
        prec = tp/(tp + fp) if (tp + fp) else 0
        rec = tp/(tp + fn) if (tp + fn) else 0
        F1 = (2*prec*rec)/(prec + rec) if (prec + rec) else 0
        if F1 > bestF1:
            bestF1 = F1
            bestEpsilon = e
    return bestF1,bestEpsilon

means,sigma = estumateGaussian(X,isCovariance = False)
pval = gaussian(Xval,means,sigma)
bestF1,bestEpsilon = selecteps(yval,pval)
bestF1,bestEpsilon#(0.8750000000000001, array([8.99985263e-05]))

6 圈出异常点 

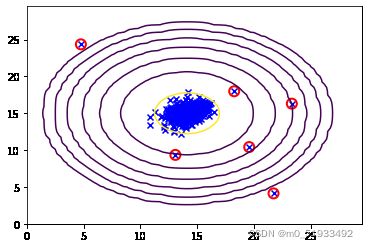
#圈出异常点
p = gaussian(X,means,sigma)
anoms = np.array([X[i] for i in range(X.shape[0]) if p[i] < bestEpsilon])
print(anoms.shape)#(6, 2)
print(len(anoms))#6
plotGaussian(X, means, sigma)
plt.scatter(anoms[:,0], anoms[:,1], s=100, marker='o', facecolors='none', edgecolors='r', linewidths=2)

 多维数据的异常检验

mat = sio.loadmat('ex8data2.mat')
mat.keys()
X2,Xval2,yval2 =mat['X'] , mat['Xval'], mat['yval'] 
X2.shape#(1000, 11)


#在验证集上发现异常点
means,sigma = estumateGaussian(X2,isCovariance = True)
pval = gaussian(Xval2,means,sigma)
bestF1,bestEpsilon = selecteps(yval2,pval)#用验证集的数据找到最佳eps
p = gaussian(X2,means,sigma)
anoms_ = [X2[i] for i in range(len(X2)) if p[i] < bestEpsilon ]#用训练集数据跟验证集得出的eps做比较判断异常点
len(anoms_ )

anoms = np.array(anoms_ )

#输出结果
print('Best epsilon found using cross-validation: %e\n' %bestEpsilon)
print('Best F1 on Cross Validation Set:  %f\n' %bestF1)
print('# anoms found: %d\n\n' %len(anoms))
# Best epsilon found using cross-validation: 1.755604e-18

# Best F1 on Cross Validation Set:  0.551724

# anoms found: 122