【Python】时间序列分析

I. 数据探索

1. 趋势分解

def decompose(timeseries,p=7):
    '''
    时间序列趋势分解的函数，timeseries是所需要分析的时序数据,p是需要确认的周期性的期数
    '''
    from statsmodels.tsa.seasonal import seasonal_decompose
    # 使画图中中文显示正常
    plt.rcParams['font.sans-serif']=['Heiti TC']
    plt.rcParams['axes.unicode_minus'] = False
    plt.rcParams.update({'font.size': 12})
    # 返回包含三个部分 trend（趋势部分） ， seasonal（季节性部分） 和residual (残留部分)
    decomposition = seasonal_decompose(timeseries,period=p)
    
    trend = decomposition.trend
    seasonal = decomposition.seasonal
    residual = decomposition.resid
    plt.figure(facecolor='white',figsize=(14,12))
    plt.subplot(411)
    plt.plot(timeseries, label='Original({})'.format(timeseries.name))
    plt.legend(loc='best')
    plt.subplot(412)
    plt.plot(trend, label='Trend')
    plt.legend(loc='best')
    plt.subplot(413)
    plt.plot(seasonal,label='Seasonality')
    plt.legend(loc='best')
    plt.subplot(414)
    plt.plot(residual, label='Residuals')
    plt.legend(loc='best')
    plt.tight_layout()
    plt.show()
    return trend , seasonal, residual

trend,seasonal,residual = decompose(data.price,p=365)

2. 数据平稳性检验

平稳性概念：假定某个时间序列是由一系列随机过程生成的，即假定时间序列的每一个数值都是从一个概率分布中随机得到，如果满足下列条件：

• 均值u是与时间t无关的常数；
• 方差是与时间t无关的常数；
• 协方差是只与时间间隔K有关，与时间t无关的常数

则称随机时间序列是平稳的，而该随机过程是平稳随机过程。

为什么需要时间序列的平稳性？

时间序列分析方法是利用样本信息来推测总体信息。根据统计学常识，肯定是分析的随机变量越少越好，而通过每个变量获得的样本信息越多越好。但是时间序列分析的数据结构有它的特殊性，对随机序列而言，在任意时刻t的序列值Xt都是一个随机变量，而且由于时间的不可重复性，该变量在任意时刻只能获得唯一的样本观测值。所以在样本信息较少的情况下，是无法获得其他辅助信息的，如果序列平稳则可以有效解决这个问题。

2.1. 单位根检验（Dickey-Fuller test）

判断依据：如果检验统计量(TS)大于临界值(CV)，则否决原假设(即序列不是平稳的)。如果TS小于CV，则不能否决原假设(即序列是平稳的)。

from statsmodels.tsa.stattools import adfuller

temp = np.array(data)
t = adfuller(temp)  # ADF检验
output=pd.DataFrame(index=['Test Statistic Value', "p-value", "Lags Used", "Number of Observations Used","Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],columns=['value'])
output['value']['Test Statistic Value'] = t[0]
output['value']['p-value'] = t[1]
output['value']['Lags Used'] = t[2]
output['value']['Number of Observations Used'] = t[3]
output['value']['Critical Value(1%)'] = t[4]['1%']
output['value']['Critical Value(5%)'] = t[4]['5%']
output['value']['Critical Value(10%)'] = t[4]['10%']

2.2. KPSS测试

KPSS 测试,不如ADF方法流行。KPSS检验的原假设和备择假设与ADF检验相反。

from statsmodels.tsa.stattools import kpss
def kpss_test(timeseries):
    print('Results of KPSS Test:')
    kpsstest = kpss(timeseries, regression='c')
    kpss_output = pd.Series(kpsstest[0:3], index=['Test Statistic', 'p-value', '#Lags Used'])
    for key, value in kpsstest[3].items():
        kpss_output['Critical Value (%s)' % key] = value
    print(kpss_output)
kpss_test(timeseries)  

#结果显示TS>cv, p <1% 表示拒绝数据是平稳的原假设，序列不是平稳的。

2.3 对数据平稳化

• 平滑法（分析，预测），移动平均，加权移动平均法
• 对数变化：当原序列的前后数值相差较大或者数量级相差较大时。主要是为了减小数据的振动幅度，使其线性规律更加明显
• 差分

一阶差分：t(n)-t(n-1)
二阶差分：一阶差分上再做一阶差分t(n)-2t(n-1)+t(n-2)

3. 白噪声检验

Ljung-Box检验 (LB检验) 是时间序列分析中检验序列自相关性的方法。用来检验m阶滞后范围内序列的自相关性是否显著，或序列是否为白噪声。其原假设为序列是白噪声序列。

# 白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print('LB test p-value：', acorr_ljungbox(df_train.sales_ln_diff12, lags=1)[1][0])

• LB统计量小于选定置信水平下的临界值，或者 p 值大于显著性水平（如0.05），不能拒绝原假设，序列为白噪声；
• LB统计量大于选定置信水平下的临界值，或者 p 值小于显著性水平（如0.05），拒绝原假设，序列非白噪声；

对于ARIMA模型，其残差被假定为高斯白噪声序列，所以当我们用ARIMA模型去拟合数据时，拟合后我们要对残差的估计序列进行LB检验，判断其是否是高斯白噪声，如果不是，那么就说明ARIMA模型也许并不是一个适合样本的模型。

II. 机器学习模型

• AR模型认为通过时间序列过去时点的线性组合加上白噪声即可预测当前时点。
• MA模型是历史白噪声的线性组合。与AR最大的不同之处在于，AR模型中历史白噪声的影响是间接影响当前预测值的（通过影响历史时序值）。金融模型中，MA常用来刻画冲击效应，例如预期之外的事件。

ARIMA模型

AutoRegressive Integrated Moving Average

• AR: 自相关模型(AutoRegressive)
• MA: 移动平均模型(Moving Average)
• I：差分的逆过程(差分的逆过程)

ARIMA(p,d,q）的三个参数：

• p：自回归模型阶数
• d：使之成为平稳序列所做的差分阶数
• q：移动平均模型阶数

使用ARIMA模型预测数据的主要步骤包括：

1. 序列平稳化
2. 确定d参数
3. 画出acf和pacf图，确定p参数和q参数
4. 使用找到的参数拟合ARIMA模型
5. 在验证集上进行预测
6. 评估预测效果

序列平稳化

1. 当原序列的前后数值相差较大或者数量级相差较大时，一般取对数将指数趋势转化为线性趋势，而且还不会改变变量之间的统计性质，同时得到较平稳的序列。

# 对数变换
df_train['sales_ln'] = np.log(df_train.sales)

# 取一阶差分
df_train['sales_ln_diff1'] = df_train.sales_ln.diff(periods=1)
df_train.dropna(subset=['sales_ln_diff1'], inplace=True)

# 二阶差分，取步长为12
df_train['sales_ln_diff12'] = df_train.sales_ln_diff1.diff(periods=12)
df_train.sales_ln_diff12.dropna(inplace=True)


# 定义一个差分还原函数
def diff_restore(arma):
    date_index = pd.date_range(start='2020-06-01', periods=24, freq='MS')
    arma_pred = arma.forecast(steps=24)[0]  # 预测未来24个月
    diff1_pred12 = pd.Series(df_train.sales_ln_diff1[-12:].values - arma_pred[:12], index = date_index[:12])
    diff1_pred24 = diff1_pred12.append(pd.Series(diff1_pred12.values - arma_pred[12:], index = date_index[12:]))  # 二阶差分还原
    sales_ln_pred = pd.Series([df_train.sales_ln[-1]], index=[df_train.index[-1]]).append(diff1_pred24).cumsum()[1:]  # 一阶差分还原
    sales_pred = np.power(np.e, sales_ln_pred)  # 因为取对数之后进行的差分操作，所以需要取自然底数还原
    return sales_pred

确认p参数和q参数

拖尾，顾名思义，就是序列缓慢衰减，“尾巴”慢慢拖着滑下来，或者震荡衰减。而截尾则是突然截断了，像个悬崖，指序列从某个时点变得非常小

(1)p 值可从偏自相关系数（PACF）图的最大滞后点来大致判断，q 值可从自相关系数（ACF）图的最大滞后点来大致判断

# 查看自相关系数与偏相关系数
from statsmodels.graphics.tsaplots import plot_pacf, plot_acf
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12,4))
plot_acf(df_train.sales_ln_diff12, ax=ax[0]).show()
plot_pacf(df_train.sales_ln_diff12, ax=ax[1]).show()

#ACF：将有序的随机变量序列与其自身相比较，它反映了同一序列在不同时序的取值之间的相关性。
#PACF：PACF计算的是严格的两个变量之间的相关性，是剔除了中间变量的干扰之后所得到的两个变量之间的相关程度。

#预测时间序列
from statsmodels.tsa.stattools import acf,pacf
lag_acf=acf(ts_log_diff,nlags=30)
lag_pacf=pacf(ts_log_diff,nlags=30,method='ols')

(2)遍历搜索AIC和BIC最小的参数组合（因为一般通过拖尾和截尾对模型定阶，具有很强的主观性），通过比较不同差分阶数的AIC、BIC的值，取两者最小值p、q 

AIC(Akaike信息准则)和BIC(Bayes信息准则)

trend_evaluate = sm.tsa.arma_order_select_ic(train, ic=['aic', 'bic'], max_ar=6, max_ma=4)
print('train AIC', trend_evaluate.aic_min_order)
print('train BIC', trend_evaluate.bic_min_order)

模型拟合

#模型拟合
from statsmodels.tsa.arima_model import ARIMA

model = ARIMA(data, order=(2,1,2)).fit()

模型诊断

# 诊断
results.plot_diagnostics(figsize=(15, 10))
plt.show()

预测效果

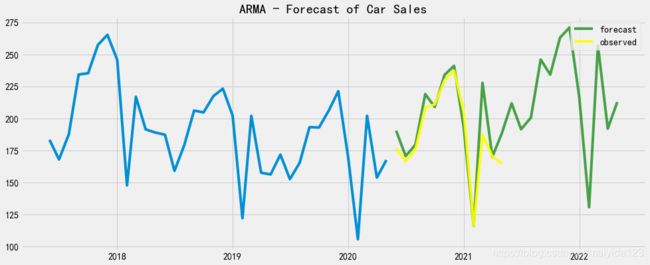
fig,ax = plt.subplots(figsize=(15,6))
ax.plot(df_train.sales[-36:])
ax.plot(sales_pred_bic, color = 'green', label = 'forecast', alpha=0.7)
ax.plot(sales_pred_bic.index[:12], df_test.values, color = 'yellow', label = 'observed', alpha=0.9)

ax.set_title("ARMA - Forecast of Car Sales")
ax.legend(loc=1)
plt.show()

预测结果评估

from sklearn.metrics import mean_absolute_error
mean_absolute_error(true, predict)

from sklearn.metrics import mean_absolute_percentage_error as mape
mape(true, predict)

官方文档：statsmodels.tsa.arima.model.ARIMA — statsmodels

Auto ARIMA

Auto ARIMA可以绕过使序列平稳化、定阶等步骤

from statsmodels.tsa.arima_model import ARIMA
import pmdarima as pm

'''
start_p: p的起始值，自回归(“AR”)模型的阶数(或滞后时间的数量),必须是正整数。
start_q: q的初始值，移动平均(MA)模型的阶数。必须是正整数。
max_p: p的最大值，必须是大于或等于start_p的正整数。
max_q: q的最大值，必须是一个大于start_q的正整数。
seasonal: 是否适合季节性ARIMA。默认是正确的。注意，如果season为真，而m == 1，则season将设置为False。
stationary: 时间序列是否平稳，d是否为零。
information_criterion：信息准则用于选择最佳的ARIMA模型。(‘aic’，‘bic’，‘hqic’，‘oob’)之一
alpha：检验水平的检验显著性，默认0.05
test: 如果stationary为假且d为None，用来检测平稳性的单位根检验的类型。默认为‘kpss’;可设置为adf
n_jobs ：网格搜索中并行拟合的模型数(逐步=False)。默认值是1，-1为使用电脑所有核心。
suppress_warnings：statsmodel中可能会抛出许多警告。如果suppress_warnings为真，那么来自ARIMA的所有警告都将被压制
error_action: 如果由于某种原因无法匹配ARIMA，则可以控制错误处理行为 (warn,raise,ignore,trace)
max_d: d的最大值，即非季节差异的最大数量。必须是大于或等于d的正整数。
trace: 是否打印适合的状态。如果值为False，则不会打印任何调试信息。值为真会打印一些
'''

smodel = pm.auto_arima(df_train.sales_ln, start_p=1, start_q=1,
                         test='adf',
                         max_p=3, max_q=3, m=12,
                         start_P=0, seasonal=True,
                         stationary=True,
                         information_criterion='aic',
                         error_action='ignore',  
                         suppress_warnings=True, 
                         stepwise=False)

smodel.summary()

pred_ln, confint_ln = smodel.predict(n_periods=24, return_conf_int=True)

SARIMAX模型

SARIMAX是在ARIMA的基础上加上季节（S, Seasonal）和外部因素(X, eXogenous)。也就是说以ARIMA基础加上周期性和季节性，适用于时间序列中带有明显周期性和季节性特征的数据。

网格搜索最佳参数

%%time
import statsmodels.api as sm
from joblib import Parallel, delayed
import itertools
from tqdm import tqdm

p = d = q = [0, 1, 2]
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in pdq]

def sarima(param, param_seasonal):
    mod = sm.tsa.statespace.SARIMAX(df_train.sales_ln,
                                    order=param,
                                    seasonal_order=param_seasonal)
    res = mod.fit()
    return param, param_seasonal, res
    
# 调用所有核心并发运行，并添加进度条
res_list = Parallel(n_jobs=-1)(delayed(sarima)(i, j) for i in tqdm(pdq) for j in seasonal_pdq)  
data = [[i, j, k.aic] for i, j, k in res_list]  
sarima_res = pd.DataFrame(data, columns=['param', 'param_seasonal', 'aic'])
sarima_res

# 查看aic最小值参数
sarima_res.loc[sarima_res.aic == sarima_res.aic.min()]

模型拟合

best_mod = sm.tsa.statespace.SARIMAX(df_train.sales_ln, 
                                order=(1,1,0), 
                                seasonal_order=(1,0,2,12))
results = best_mod.fit()
print(results.summary())

模型预测

# 预测未来24个月的销量
pred_uc = results.get_forecast(steps=24, alpha=0.05)
pred_pr = pred_uc.predicted_mean

# 获取预测的置信区间
pred_ci = pred_uc.conf_int()

#预测图
fig,ax = plt.subplots(figsize=(15,6))
ax.plot(df_train.sales[-24:])
ax.plot(pred_data.forecast, color = 'green', label = 'forecast', alpha=0.7)
ax.plot(pred_data.index[:12], df_test.values, color = 'yellow', label = 'observed', alpha=0.7)
ax.fill_between(pred_data.index, 
                 pred_data.lower_ci_95, 
                 pred_data.upper_ci_95, 
                 color='grey', alpha=0.5,label = '95% confidence interval')

ax.set_title("SARIMA - Forecast of Car Sales")
ax.legend()
plt.show()

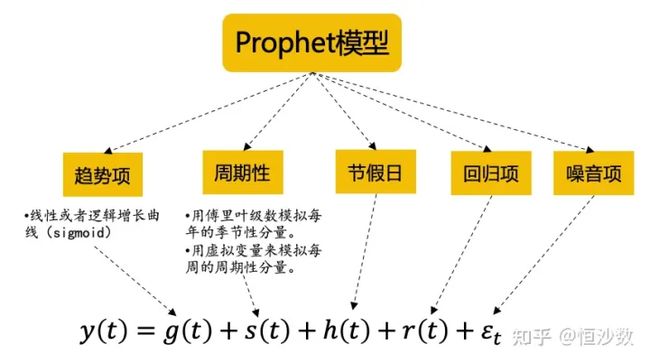
Prophet模型

Prophet由Facebook开源的基于python和R语言的数据预测工具，是一种基于时间和变量值结合时间序列分解和机器学习的拟合来做的时序模型；Prophet模型简单、容易上手、并且在建模过程中考虑了趋势线、季节性、周期性、以及外生变量等因素的影响，预测效果好，相对于传统时序模型有很大优势。

ARIMA模型只适合短期预测，而且在模型中没有考虑周期性、节假日以及外生回归量等因素。虽然ARIMA的升级版ARIMAX和SARIMA模型考虑了这些因素，但是从长期预测效果来看，仍然不如Prophet。

Prophet模型的基本原理如下图所示，在构建时间序列模型的时候，综合考虑了趋势、周期、节假日及外生回归项等因素：

from fbprophet import Prophet

m = Prophet(yearly_seasonality=True,growth='logistic',holidays=holidays_df)
#growth是时序变化趋势，有线性(linear)和非线性（logistic）两种
#holidays设置节假日的日期,我们令其等于上文中设置的holidays_df

#我们增加行业另外竞品数据作为回归项
for i in data_prophet_hist.columns[1:-3]:
    m.add_regressor(i)
m.fit(data_prophet_hist) # 放入历史数据训练

III. 时间序列预测的评价指标

时间序列预测的评价指标可以分为两类，一类是scale无关的（如smape、rmsle、mape等），一类是scale相关的（如mse、rmse、mae、nd等）。Scale无关的，即不管每个样本点的取值多大，对最终loss的贡献都是差不多的，因为这些指标计算的都是预测值相对于真实值的偏差百分比。而scale相关的指标，数值越大对loss的贡献就越大，因为它们直接计算预测值和真实值的差值。

 在选择指标时，如果更关注大值样本的效果，可以用scale相关的指标；如果更关注全局所有样本的效果，可以用scale无关的指标。对于scale无关的指标还要注意一点，在一些场景中，小值样本比大值样本多得多，数据呈现长尾部分。这种情况下使用scale无关指标，则更偏向于看小值样本效果。同时，小值样本可能存在更大的误差，比如真实值是1，预测值是2，这偏差就是100%了，小样本本来就噪声大。如果用scale无关指标在这类数据上评估，很可能反映的是拟合噪声的效果。因此更合适的做法是对测试集做一个采样，小值样本、大值样本保留差不多的数量，才能更科学的评价模型效果。

IV. Python库

	Forecasting	Classsification	Anomaly Detection	Segmentation	TSFeature
Prophet	✅
Kats	✅		✅		✅
GluonTS	✅		✅		✅
NeuralProphet	✅		✅		✅
arch	✅
AtsPy	✅
banpei			✅
cesium					✅
darts	✅
PaddleTS	✅				✅

模型

Model	Univariate	Multivariate	Probabilistic	Multiple-series training
ARIMA	✅		✅
VARIMA	✅	✅
AutoARIMA	✅
ExponentialSmoothing	✅		✅
Theta and FourTheta	✅
Prophet	✅		✅
FFT (Fast Fourier Transform)	✅
RegressionModel (incl RandomForest, LinearRegressionModel and LightGBMModel)	✅	✅		✅
RNNModel (incl. LSTM and GRU); equivalent to DeepAR in its probabilistic version	✅	✅	✅	✅
BlockRNNModel (incl. LSTM and GRU)	✅	✅	✅	✅
NBEATSModel	✅	✅	✅	✅
TCNModel	✅	✅	✅	✅
TransformerModel	✅	✅	✅	✅
TFTModel (Temporal Fusion Transformer)	✅	✅	✅	✅
Naive Baselines	✅

References

容易上手的时间序列分析2：Prophet模型 - 知乎

Python数据分析案例-分别使用时间序列ARIMA、SARIMAX模型与Auto ARIMA预测国内汽车月销量_吴下阿泽的博客-CSDN博客