机器学习之支持向量机SVM(自学笔记)
文章目录
-
- 一,概念
- 二,SVM原理
- (一)原理介绍
- (二)宽松条件下的SVM
- (三)支持向量
- 三,SVM的目标优化函数
- 四,核方法
一,概念
支持向量机(SVM):主要应用于二分类问题,是一种有监督的学习。其基本思想是在特征空间中寻找最大的分隔超平面使得数据得到准确的分类。
二,SVM原理
(一)原理介绍
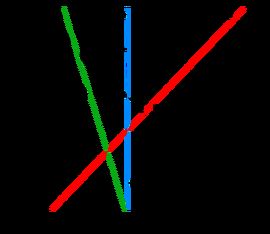
如图所示,如果想将黑色的点和白色的点分开,最好的选择是H3这条线,其余的线都不能将两类点分开。
如果H3这条直线的方程为: y = w 1 x + w 0 y=w_1x+w_0 y=w1x+w0 ,
将H3上方的黑点标记为y=1类,将H3下方的点标记为y=-1类。上图中距离H3最近的一个黑点和一个白点被称为边界点。其余的点为各类的内部点。
用公式表示如下:
y = 1 类, w 1 x + w 0 ≥ 1 y = − 1 类, w 1 x + w 0 ≤ − 1 y=1类,w_1x+w_0 \ge 1 \\ y=-1类,w_1x+w_0 \le -1 y=1类,w1x+w0≥1y=−1类,w1x+w0≤−1
上述公式可以同一写成如下形式:
y ( w 1 x + w 0 ) ≥ 1 y(w_1x+w_0) \ge 1 y(w1x+w0)≥1
由点到直线的距离公式可知,边界点到分类线的距离为:
d = 1 w 1 2 d=\frac{1}{\sqrt{w_1^2}} d=w121
所以要让d最大化,即边界点的距离最大,提高泛化能力,所以要最小化 w 1 2 \sqrt{w_1^2} w12
(二)宽松条件下的SVM
存在一些点在分类线外但是在边界线里,换句话说,有一些点在边界线和分类线之间,所以就需要放宽SVM的条件
形式如下:
y ( w 1 x + w 0 ) ≥ 1 − α y(w_1x+w_0) \ge 1 - \alpha y(w1x+w0)≥1−α
- 当数据点为内部点或者边界点的时候, α \alpha α=0
- 当数据点在边界点和分类线之间的时, 0 < α < 1 0 < \alpha < 1 0<α<1
- 当数据点在另一边边界点和分类线之间, α ≥ 1 \alpha \ge 1 α≥1
由此可知 α \alpha α 越小越好,模型的分类效果越好
由(一)知,要最小化 w 1 2 \sqrt{w_1^2} w12 ,在此基础上要最小化 α \alpha α
(三)支持向量
每个边界点都是一个向量,所以,边界点也称为支持向量。
三,SVM的目标优化函数
由二指,我们的优化目标,在此基础上考虑所有的样本n
得到,
( ∣ ∣ w ∣ ∣ ) 2 + C ∑ i = 1 n α i (||w||)^2+C\sum\limits_{i=1}^n \alpha_i (∣∣w∣∣)2+Ci=1∑nαi
让上式最小化,并且所有的训练样本满足:
y i ( w T x i + w 0 ) ≥ 1 − α i y_i(w^Tx_i+w_0) \ge 1 - \alpha_i yi(wTxi+w0)≥1−αi
四,核方法
核方法是SVM拥有的特殊方法。
遇到线性不可分的问题,可以通过升维的方法让其变成线性可分。核方法也是解决线性不可分发方法之一。
对于输入空间中的非线性分类问题,可以通过非线性变换将它转化为某个维特征空间中的线性分类问题,在高维特征空间中学习线性支持向量机。由于在线性支持向量机学习的对偶问题里,目标函数和分类决策函数都只涉及实例和实例之间的内积,所以不需要显式地指定非线性变换**,**而是用核函数替换当中的内积。
介绍两种核函数
高斯核函数
K ( x , z ) = e x p ( − ‖ x − z ‖ 2 2 σ 2 ) K(x,z)=exp(−\frac{‖x−z‖^2 }{2σ^2}) K(x,z)=exp(−2σ2‖x−z‖2)
多项式核函数
K ( x , z ) = ( a < x , z > + c ) d K(x,z) = (a
函数
K ( x , z ) = e x p ( − ‖ x − z ‖ 2 2 σ 2 ) K(x,z)=exp(−\frac{‖x−z‖^2 }{2σ^2}) K(x,z)=exp(−2σ2‖x−z‖2)
多项式核函数
K ( x , z ) = ( a < x , z > + c ) d K(x,z) = (a