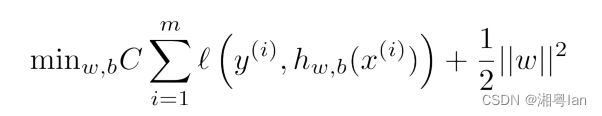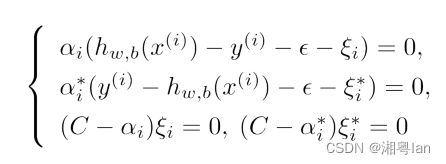机器学习05|一万五字:SVM支持向量机02 【jupyter代码详解篇】
文章目录
- Jupyter实现
-
- 任务一 从DataSet.txt中导入数据,获得训练集以及标签。
- 任务二 调整alpha的值
- 任务三 上述原理过程中,需要计算真实值与预测值之间的误差,定义一个函数ComputeEk。
- 任务四 选取最大 ∣ E i − E j ∣ |E_i-E_j| ∣Ei−Ej∣最大的j,并返回j以及 E j E_j Ej
- 任务五 计算误差值并存入缓存,在对alpha值进行优化之后会用到这个函数
- 任务六 根据计算出的拉格朗日乘子计算出权重向量W,计算公式如下:
- 任务七 画出SVM的决策边界
- 任务八 实现径向基核函数
- 任务九 SVR:线性回归实现
- 任务十 SVR:非线性回归
本文用到的所有数据 机器学习05:SVM【代码及数据文件】
本文为SVM支持向量机系列第二篇,主要讲解代码实现及解析。详细实现原理及公式推导,请参考第一篇博客:
机器学习05|一万五字:SVM支持向量机01 【原理详解篇】
Jupyter实现
现在我们来总结下SMO算法的步骤
1 第一步选取一对 α i 和 α j ,选取方法使用启发式方法 \alpha_i和\alpha_j,选取方法使用启发式方法 αi和αj,选取方法使用启发式方法。
2 第二步,固定 除 α i 和 α j 之外的其它参数 , 确定 W 极值条件下的 α i , α j 由 α i 表示。 除\alpha_i和\alpha_j之外的其它参数,确定W极值条件下的\alpha_i,\alpha_j由\alpha_i表示。 除αi和αj之外的其它参数,确定W极值条件下的αi,αj由αi表示。
3 第三步,更新乘子,选取乘子的方式如下:
先扫描所有乘子,把第一个违反 K K T 条件的作为更新对象,令为 α 1 先扫描所有乘子,把第一个违反KKT条件的作为更新对象,令为\alpha_1 先扫描所有乘子,把第一个违反KKT条件的作为更新对象,令为α1
在所有不违反 K K T 条件的乘子中,选择使 ∣ E 1 − E 2 ∣ 最大的 α 2 进行更新,使得能最大限度增大目标函数的值。 在所有不违反KKT条件的乘子中,选择使|E_1-E_2|最大的\alpha_2进行更新,使得能最大限度增大目标函数的值。 在所有不违反KKT条件的乘子中,选择使∣E1−E2∣最大的α2进行更新,使得能最大限度增大目标函数的值。
4 最后,每次更新完两个乘子的优化后,都需要再重新计算b,以及对应的 E i E_i Ei值。
经过前面几节的铺垫,我们了解SVM对偶形式的求解,现在我们就来用代码实现SVM。
任务一 从DataSet.txt中导入数据,获得训练集以及标签。
定义函数LoadData(filename),参数为文件名,返回训练数据集以及标签。数据集由两个特征 X 1 和 X 2 X_1和X_2 X1和X2构成
#导入相应的库包
from numpy import *
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore",category=DeprecationWarning) #消除警告
def LoadData(filename):
data = []
label = []
with open(filename) as f:
for line in f.readlines(): #按行读取
### START THE CODE ###
lineArr = line.strip().split(' ') #消除分隔符
num = np.shape(lineArr)[0]
data.append(list(map(float,lineArr[0:num-1]))) #将特征存放到Data中
label.append(float(lineArr[num-1])) #将标签存放到Label中
### END THE CODE ###
return data,label
获取训练集,数据和标签
TrainData, TrainLabel = LoadData('DataSet.txt')
print ("TrainData = ",TrainData[:3])
print ("TrainLabel = ",TrainLabel[:3])
TrainData = [[3.542485, 1.977398], [3.018896, 2.556416], [7.55151, -1.58003]]
TrainLabel = [-1.0, -1.0, 1.0]
输出:
TrainData = [[3.542485, 1.977398], [3.018896, 2.556416], [7.55151, -1.58003]]
TrainLabel = [-1.0, -1.0, 1.0]
定义所需操作的数据结构DataOp如下
class DataOp(object):
def __init__(self,data,label,C,toler): #定义构造函数
self.X = data #数据
self.label = label #标签
self.C = C #松弛变量
self.tol = toler #容忍度
self.m = shape(data)[0] #特征向量的第一个维度
self.alpha = mat(zeros((self.m,1))) #Alpha个数初始化
self.b = 0 #步长
self.Cache = mat(zeros((self.m,2))) #第一列给出是否有效 第二列给出的是实际的E值
我们利用上述定义的数据结构来表达我们整个训练模型的过程需要的参数以及数据,初始化一个DataOp对象
oS = DataOp(mat(TrainData), mat(TrainLabel).transpose(), 0.6, 0.001)
在选择乘子过程中,我们需要选中两个不同的乘子,所以当我们固定了其中一个乘子,就需要选出不同于第一个乘子的第二个乘子。我们定义一个函数SelectAlpha来实现这个过程。
函数:SelectAlpha(i,m)
作用:随机选择一个整数j,(0<=j<=m-1 && j!=i)
参数:i第一个乘子的下标,m所有alpha的个数
返回:一个随机选择不同于i的下标j
def SelectAlpha(i,m):
j = i
while (j == i):
j = int(random.uniform(0,m))
return j
任务二 调整alpha的值
根据如下规则来对我们计算出的alpha进行调整。
1 α 2 n e w , w n c > H {\alpha_2}^{new,wnc}>H α2new,wnc>H
α 2 n e w = H {\alpha_2}^{new}=H α2new=H
2 L < = α 2 n e w , w n c < = H L<={\alpha_2}^{new,wnc}<=H L<=α2new,wnc<=H
α 2 n e w = α 2 n e w , w n c {\alpha_2}^{new}={\alpha_2}^{new,wnc} α2new=α2new,wnc
3 α 2 n e w , w n c < L {\alpha_2}^{new,wnc}
α 2 n e w = L {\alpha_2}^{new}=L α2new=L
函数:ResetAlpha(Alphaj,low,high)
作用:调整Alphaj(即 α j \alpha_j αj)的值,使得low<=Alphaj<=high,调整幅度尽可能小
参数:Alphaj 目标值, low 最小值, high最大值
返回:调整后的Alphaj
def ResetAlpha(Alphaj,low,high):
### STARD CODE HERE ###
if Alphaj >= high:
Alphaj = high
elif Alphaj <= low:
Alphaj = low
### END CODE HERE ###
return Alphaj
a = 10
b = ResetAlpha(a,11,20)
c = ResetAlpha(a,1,8)
print("b = ", b)
print("c = ", c)
b = 11
c = 8
输出:
b = 11
c = 8
任务三 上述原理过程中,需要计算真实值与预测值之间的误差,定义一个函数ComputeEk。
函数 ComputeEk(os,k)
作用:求Ek误差 = 预测值 - 真实值。
真实值即样本标签,以下公式计算预测值 f ( x ) = ∑ i = 1 n α i y i < x i , x > + b f(x)=\sum_{i=1}^{n}\alpha_iy_i
参数:os DataOp对象,k 具体的某一行
返回:预测值与真实结果对比,计算误差Ek
def ComputeEk(os,k):
PredictK = float(multiply(os.alpha,os.label).T * (os.X*os.X[k,:].T)) + os.b
### START CODE HERE ###
Ek = PredictK - os.label[k,:]
### END CODE HERE ###
return Ek
Ek1 = ComputeEk(oS,25)
Ek2 = ComputeEk(oS,30)
print ("Ek1 = ", Ek1)
print ("Ek2 = ", Ek2)
Ek1 = [[-1.]]
Ek2 = [[1.]]
输出:
Ek1 = -1.0
Ek2 = 1.0
任务四 选取最大 ∣ E i − E j ∣ |E_i-E_j| ∣Ei−Ej∣最大的j,并返回j以及 E j E_j Ej
函数:SelectMaxJ(i,oS,Ei)
作用:返回差值最大的j和对应的Ej,选择第二个(内循环)值以保证每次优化中采用最大步长。
这里的目标是选择合适的第二个alpha值以保证每次优化中采用最大步长
该函数的误差与第一个alpha值Ei和下标i有关。
参数:
i 具体的第i行
oS DataOp对象
Ei 预测值与真实值对比,计算Ei
返回:
j 随机选出的第j行
Ej 预测结果与真实值对比,计算误差Ej
def SelectMaxj(i,oS,Ei):
MaxK = -1 #保存最大下标值
MaxDeltaE = 0 #保存最大步长
Ej = 0
oS.Cache[i] = [1,Ei] #首先将输入值Ei在缓存中设置为有效的。这里意味着它已经计算好了
List = nonzero(oS.Cache[:,0].A)[0]
if (len(List)) > 1: # 在所有的值上进行循环,并选择使得改变最大的那个值
for k in List:
if k == i:
continue #不计算
### START CODE HERE ###
Ek = ComputeEk(oS,k)
DeltaE = abs(Ek - Ei) # 计算DeltaE
if (DeltaE > MaxDeltaE): #DeltaE > MaxDeltaE , 则进行更新
MaxDeltaE = DeltaE #最大值更新
MaxK = k #更新下标
Ej = Ek #替换Ej
### END CODE HERE ###
return MaxK, Ej
else: #如果是第一次循环,则随机选择一个alpha
j = SelectAlpha(i,oS.m)
Ej = ComputeEk(oS,j)
return j,Ej
Data = [[3.542485, 1.977398], [3.018896, 2.556416], [7.55151, -1.58003], [2.114999, -0.004466], [8.127113, 1.274372]]
Label = [-1.0, -1.0, 1.0, -1.0, 1.0]
TestOs = DataOp(mat(Data),mat(Label).transpose(),0.6,0.001)
TestEi = ComputeEk(TestOs,0)
TestOs.Cache[1] = [1,ComputeEk(TestOs,1)]
TestOs.Cache[2] = [1,ComputeEk(TestOs,2)]
TestOs.Cache[3] = [1,ComputeEk(TestOs,3)]
TestOs.Cache[4] = [1,ComputeEk(TestOs,4)]
Testj,TestEj = SelectMaxj(0,TestOs,TestEi)
print ("Testj = ",Testj)
print ("TestEj = ", TestEj)
Testj = 2
TestEj = [[-1.]]
输出:
j = 2
Ej = -1.0
任务五 计算误差值并存入缓存,在对alpha值进行优化之后会用到这个函数
函数:updateEk(oS,k)
作用:计算误差值并存入缓存os.Cache,在对alpha值进行优化之后会用到这个函数
参数:
Os DataOpt对象
k 某一列的行号
返回:无
例如某行为oS.Cache[k] = [1,Ek] 其中1表示有效。
def updataEk(oS,k):
###START THE CODE ###
Ek = ComputeEk(oS,k) #计算Ek
oS.Cache[k] = [1,Ek] #更新第k行的oS.Cache[k]
###END THE CODE ###
TestOs = DataOp(mat(Data),mat(Label).transpose(),0.6,0.001)
updataEk(TestOs,0)
updataEk(TestOs,1)
updataEk(TestOs,2)
print ("TestOs.Cache[0] = ",TestOs.Cache[0])
print ("TestOs.Cache[1] = ",TestOs.Cache[1])
print ("TestOs.Cache[2] = ",TestOs.Cache[2])
TestOs.Cache[0] = [[1. 1.]]
TestOs.Cache[1] = [[1. 1.]]
TestOs.Cache[2] = [[ 1. -1.]]
输出:
TestOs.Cache[0] = [[1. 1.]]
TestOs.Cache[1] = [[1. 1.]]
TestOs.Cache[2] = [[1. -1.]]
SMO算法是通过一个外循环来选择第一个alpha值得,并且其选择过程会在两种方式之间交替:一种方式是在所有数据集上进行单遍扫描,另一种方式则是在非边界alpha中实现单遍扫描。而所谓非边界alpha指的就是那些不等于边界0或C的alpha的值。对整个数据集的扫描相当容易,而实现非边界alpha值得扫描时,首先需要建立这些alpha值的列表,然后再对这个表进行遍历。同时,该步骤会跳过那么已知的不会改变的alpha的值。
在选择第一个alpha值后,算法会通过一个内循环来选择第二个alpha值。在优化过程中,会通过最大步长的方式来获得第二个alpha值。我们建立一个全局的缓存用于保存误差值,并从中选择使得步长最大的alpha值(Ei-Ej)
首先我们来看实现内循环的代码,如何选择另外第二个alpha乘子。
函数:InsideCycle(i,oS)
作用:SMO算法内循环选择第二个alpha值
参数:
i 具体某一行
oS DataOp对象
返回:
0 找不到最优值
1 找到了最优值,并且存储到oS.Cache中
def InsideCycle(i,oS):
Ei = ComputeEk(oS,i) #求Ek误差
#约束条件(KKT条件是解决最优化问题时用到的一种方法。我们这里提到的最优化问题通常
#是指对于给定的某一函数,求其在指定作用域上的全局最小值
#0<=alpha[i]<=C,但由于0和C是边界值,我们无法进行优化,因为需要升高一个alpha和降低一个alpha。
#表示发生错误的概率:label[i]*Ei ,如果超出toler,才需要优化。至于正负号,考虑绝对值就行
#检验训练样本(xi,yi)是否满足KKT条件
#yi*f(xi) >= 1 and alpha = 0 (outside the boundary)
#yi*f(xi) == 1 0
#yi*f(xi) <= 1 and alpha = C (between the boundary)
if ((oS.label[i] * Ei < -oS.tol) and (oS.alpha[i] < oS.C)) or ((oS.label[i] * Ei > oS.tol) and (oS.alpha[i] > 0)):
#选择最大的误差对应的j进行优化。
j,Ej = SelectMaxj(i,oS,Ei)
IOldAlpha = oS.alpha[i].copy()
JOldAlpha = oS.alpha[j].copy()
#L 和 H将用于将alpha[j]调整到0-C之间。如果L == H,就不做任何改变,直接Return 0
if (oS.label[i] != oS.label[j]):
L = max(0,oS.alpha[j] - oS.alpha[i])
H = min(oS.C, oS.C + oS.alpha[j] - oS.alpha[i])
else:
L = max(0,oS.alpha[j] + oS.alpha[i] - oS.C)
H = min(oS.C, oS.alpha[j] + oS.alpha[i])
if L == H:
#print ("L == H")
return 0
#eva 是alpha[j]的最优修改量,如果eva==0,需要退出for循环当前迭代过程
eva = 2.0 * oS.X[i, :] * oS.X[j, :].T - oS.X[i, :] * oS.X[i, :].T - oS.X[j, :] * oS.X[j, :].T
if eva >= 0:
#print("eva >= 0")
return 0
#计算一个新的alpha[j]值
oS.alpha[j] -= oS.label[j] * (Ei-Ej) / eva
#并使用辅助函数,以及L和H对其进行调整
oS.alpha[j] = ResetAlpha(oS.alpha[j],L,H)
#更新缓存误差
updataEk(oS,j)
#检查alpha[j]是否只是轻微的改变,如果是的话,就退出for循环
if (abs(oS.alpha[j] - JOldAlpha) < 0.00001):
return 0
#然后alpha[i]和alpha[j]做同样的修改,虽然改变的大小一样,但是改变的方向相反
oS.alpha[i] += oS.label[j] * oS.label[i] * (JOldAlpha - oS.alpha[j])
#更新误差缓存
updataEk(oS,i)
#在对alpha[i],alpha[j]进行优化之后,给这个两个alpha值设置一个常数b。
'''
w= Σ[1~n] ai*yi*xi => b = yj Σ[1~n] ai*yi(xi*xj)
所以: b1 - b = (y1-y) - Σ[1~n] yi*(a1-a)*(xi*x1)
为什么减2遍? 因为是 减去Σ[1~n],正好2个变量i和j,所以减2遍
'''
b1 = oS.b - Ei - oS.label[i] * (oS.alpha[i] - IOldAlpha) * oS.X[i, :] * oS.X[i, :].T - oS.label[j] * (oS.alpha[j] - JOldAlpha) * oS.X[i, :] * oS.X[j, :].T
b2 = oS.b - Ej - oS.label[i] * (oS.alpha[i] - IOldAlpha) * oS.X[i, :] * oS.X[j, :].T - oS.label[j] * (oS.alpha[j] - JOldAlpha) * oS.X[j, :] * oS.X[j, :].T
if (0 < oS.alpha[i]) and (oS.C > oS.alpha[i]):
oS.b = b1
elif (0 < oS.alpha[j]) and (oS.C > oS.alpha[j]):
oS.b = b2
else:
oS.b = (b1+b2) / 2.0
return 1
else:
return 0
接下来我们实现SMO算法的外循环,外循环的结束迭代条件是:迭代次数达到最大迭代次数 或者 循环遍历所有alpha后,没有alpha改变。
函数:Smo(oS,IterStep)
作用:SMO算法外循环,计算出拉格朗日乘子以及模型的常量b
参数:
oS DataOp对象
IterStep 退出前的最大循环次数
返回:
b 模型的常量值
alpha 拉格朗日乘子
def Smo(oS,IterStep):
iter = 0 #迭代次数
EntireSet = True #是否遍历了没有遍历整个alpha值
AlphaChanged = 0 #alpha改变的次数
#循环迭代结束 或者 循环遍历所有alpha后,AlphaChanged还是没变化
while (iter < IterStep) and ((AlphaChanged > 0) or (EntireSet)):
AlphaChanged = 0
#当EntireSet = True or 非边界alpha对没有了;就开始寻找alpha对,然后决定是否else。
if EntireSet:
#在数据集上遍历所有可能的alpha
for i in range(oS.m):
#是否存在alpha对,存在就+1
AlphaChanged += InsideCycle(i,oS)
iter += 1
#对已存在alpha对,选出非边界的alpha值,进行优化。
else:
#遍历所有非边界alpha值,进行优化。
nonBoundIs = nonzero((oS.alpha.A > 0) * (oS.alpha.A < oS.C))[0]
for i in nonBoundIs:
AlphaChanged += InsideCycle(i,oS)
iter += 1
#如果找到alpha对,就优化非边界alpha值,否则,就重新进行寻找,如果寻找一遍 遍历所有的行还是没找到,就退出循环。
if EntireSet:
EntireSet = False
elif (AlphaChanged == 0):
EntireSet = True
return oS.b, oS.alpha
下面调用SMO算法,计算常量b以及a拉格朗日乘子alpha[50:55]。
b, alphas = Smo(oS, 40)
print ("b = ", b)
print ("alphas = ",alphas[50:55])
b = [[-2.89901748]]
alphas = [[0.]
[0.]
[0.]
[0.]
[0.]]
任务六 根据计算出的拉格朗日乘子计算出权重向量W,计算公式如下:
W = ∑ i = 1 n α i y i x i W=\sum_{i=1}^{n}\alpha_iy_ix_i W=i=1∑nαiyixi
函数:ComputeW(alphas,data,label)
作用:基于alphas计算W
参数:
alphas:拉格朗日乘子
data:特征数据集
label:对应的标签数据
返回:
W:权重向量
def ComputeW(alphas,data,label):
Data = mat(data) #转换为矩阵形式
Label = mat(label).transpose()
m,n = shape(Data) #数据的维度
w = zeros((n,1))
### START THE CODE ###
for i in range(n): #根据计算公式求取w
for j in range(m):
w[i] =w[i] + alphas[j] * Label[j] * Data[j,i]
### END THE CODE ###
return w
Testalphas =[[0. ],[0. ],[0.08999025],[0. ],[0.04439791]]
w = ComputeW(Testalphas,TrainData[50:55],TrainLabel[50:55])
print ("w = ", w)
w = [[-0.02568303]
[ 0.04319313]]
输出:
w = [[-0.02568303]
[ 0.04319313]]
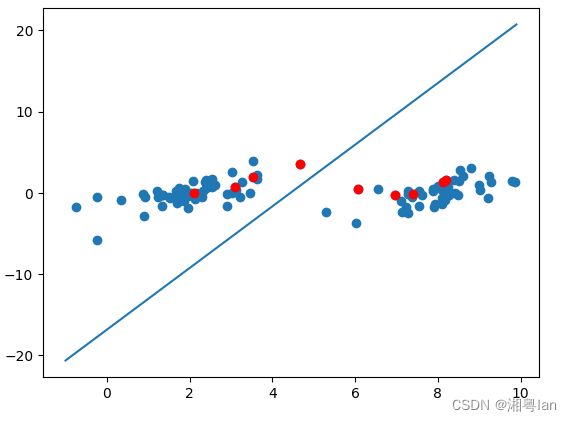
任务七 画出SVM的决策边界
定义PlotSVM函数,根据训练数据,标签,W,b,alphas画出决策边界。
正负样本用不同颜色标注。
W = ComputeW(alphas,TrainData,TrainLabel)
def PlotSVM(data,label,W,b,alphas):
Data = mat(data)
Label = np.squeeze(label)
#b 原来是矩阵 先转化为数组类型后其数组大小为(1,1),然后后面加[0],变为(1,)
b = array(b)[0]
fig = plt.figure()
figure = fig.add_subplot(111)
figure.scatter(Data[:,0].flatten().A[0],Data[:,1].flatten().A[0])
x = arange(-1.0,10.0,0.1)
y = (-b-W[0,0]*x)/ W[1,0] #画出分隔线
figure.plot(x,y)
### START THE CODE ###
for i in range(100): #找到支持向量,并在图中标红
if alphas[i]>0.0:
figure.plot(Data[i,0],Data[i,1],'ro') #将正负样本点画在画布上
###END THE CODE ###
plt.show()
PlotSVM(TrainData,TrainLabel,W,b,alphas)
径向基函数是SVM中常用的一个核函数。径向基函数是一个采用向量作为自变量的函数,能够基于向量距离输出一个标量。这个距离可以是从<0,0>向量或者其他向量开始计算的距离。接下来,我们将会使用到径向基函数的高斯版本,其具体公式如下:
k ( x 1 , x 2 ) = e x p ( − ∥ x 1 − x 2 ∥ 2 2 δ 2 ) k(x_1,x_2)=exp(\frac{-{{\Vert}x_1-x_2\Vert}^2}{2\delta^2}) k(x1,x2)=exp(2δ2−∥x1−x2∥2)
其中, δ \delta δ是用户定义的用于确定达到率或则说函数值跌落到0的速度参数。
任务八 实现径向基核函数
函数名:KernelTransform(Data,DataI,Para)
作用:将数据映射到高纬空间
参数:
Data 数据集
DataI 数据集中的第i行数据
papa:径向基函数中的 δ \delta δ参数
def KernelTransform(Data,DataI,Para):
#计算Data的维度 【m,n】
m,n = shape(Data)
K = mat(zeros((m,1)))
Data = np.array(Data)
### START THE CODE ###
for j in range(m):
deltaRow = Data[j,:] - DataI
deltaRow = mat(deltaRow)
K[j] = deltaRow*deltaRow.T
K = exp(K/(-2*Para**2)) #按照径向基函数公式求取K
### END THE CODE ###
return K
TestData = [[3.542485, 1.977398], [3.018896, 2.556416], [7.55151, -1.58003], [2.114999, -0.004466], [8.127113, 1.274372]]
TestDataI = [3.018896, 2.556416]
TestPara = 0.8
Result = KernelTransform(TestData,TestDataI,TestPara)
print ("Result = ", Result)
Result = [[6.21201706e-01]
[1.00000000e+00]
[1.67499988e-13]
[3.14534050e-03]
[3.88031058e-10]]
输出:
Result = [[6.21201706e-01]
[1.00000000e+00]
[1.67499988e-13]
[3.14534050e-03]
[3.88031058e-10]]
接下来我们导入KernnelTrainData数据进进行训练,每一行包括两个特征以及一个标签。然后利用SMO算法计算出拉格朗日乘子以及b,利用核函数转换计算K。最后进行预测并计算出预测错误率。
def LoadData(filename):
data = []
label = []
with open(filename) as f:
for line in f.readlines(): #按行读取
### START THE CODE ###
lineArr = line.strip().split('\t') #消除分隔符
num = np.shape(lineArr)[0]
data.append(list(map(float,lineArr[0:num-1]))) #将特征存放到Data中
label.append(float(lineArr[num-1])) #将标签存放到Label中
### END THE CODE ###
return data,label
def TrainAccuracy(TrainFileName,TestFileName,P,C,Toler,MaxIter):
#导入数据
Data,Label = LoadData(TrainFileName)
#高斯核参数
Para = P
#转换为mat格式
Data = mat(Data)
Label = mat(Label).transpose()
#计算拉格朗日乘子以及b
oS = DataOp(Data,Label,C,Toler)
b,alphas = Smo(oS,MaxIter)
#获取alpha>0的行数
UnZero = nonzero(alphas.A > 0)[0]
SelectData = Data[UnZero]
SelectLabel = Label[UnZero]
SelectAlphas = alphas[UnZero]
#获取Data的维度
m, n = shape(Data)
#获取测试数据集
TestData,TestLabel = LoadData(TestFileName)
TestCount = 0
#转换格式
TestData = mat(TestData)
TestLabel = mat(TestLabel).transpose()
m,n = shape(TestData)
#遍历测试集每一行数据
for i in range(m):
#核函数转换
K = KernelTransform(SelectData,TestData[i],Para)
TestPredictValue = K.T*multiply(SelectLabel,SelectAlphas) + b
#测试准确度
if sign(TestPredictValue) != sign(TestLabel[i]):
TestCount += 1
print("The Test Error Rate is: %.1f%%" % (float(TestCount)*100 / m))
#训练数据
TrainFileName = 'KernelTrainData.txt'
#测试数据
TestFileName = 'KernelTestData.txt'
#SMO算法参数
C = 210
Toler = 0.0001
MaxIter = 10000
#径向基参数
Para = 0.12
TrainAccuracy(TrainFileName,TestFileName,Para,C,Toler,MaxIter)
The Test Error Rate is: 10.0%
输出:
The Test Error Rate is: 20.0%
由以上结果可以看到,应用高斯函数进行SVM分类,我们达到了80左右%的准确率,事实上你可以修改参数,来获得更加优化的模型。
通过以上的学习,我想你已经对SVM的原理以及和核函数有了一定的了解。
SVR算法
传统的回归模型通常直接基于模型输出f(x)与真实输出y之间的差来计算损失,只有当两者完全相同时,损失才为0。而SVR加入了一个ε参数,意为我们可以容忍f(x)与y最多有ε偏差,如下图
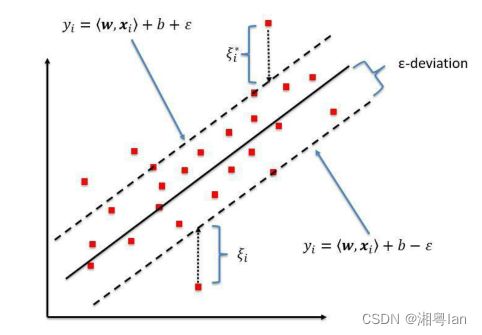
也就是说,在虚线之间的部分不进行损失计算,他们的损失为0,而只计算虚线以外的点的损失,因此他的对应损失函数为:
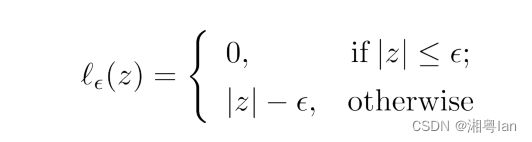
引入松弛因子 ξ i ξ_i ξi、 ξ i ∗ ξ_i^* ξi∗,SVR的优化问题变为:
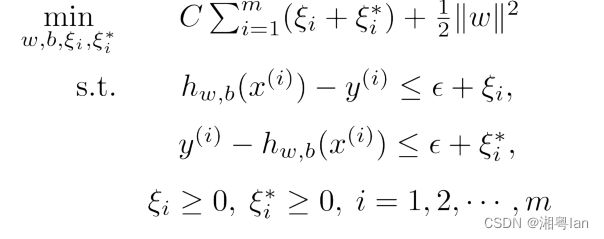
其中 h w , b ( x ) = w T x + b h_{w,b}(x)=w^Tx+b hw,b(x)=wTx+b
然后引入拉格朗日乘子,得到对应拉格朗日函数:
L ( w , b , α , α ∗ , ξ , ξ ∗ , r i , r i ∗ ) = 1 2 ∥ w ∥ 2 + C ∑ i = 0 m ( ξ i + ξ i ∗ ) − ∑ i = 1 m r i ξ i − ∑ i = 1 m r i ∗ ξ i ∗ + ∑ i = 1 m α i ( h w , b ( x i ) − y i − ε − ξ i ) + L(w,b,α,α^*,ξ,ξ^*,r_i,r_i^*)=\frac{1}{2}{\parallel w\parallel}^2+C\sum_{i=0}^{m}(ξ_i+ξ_i^*)-\sum_{i=1}^{m}r_iξ_i-\sum_{i=1}^{m}r_i^*ξ_i^*+\sum_{i=1}^{m}α_i(h_{w,b}(x^i)-y^i-ε-ξ_i)+ L(w,b,α,α∗,ξ,ξ∗,ri,ri∗)=21∥w∥2+Ci=0∑m(ξi+ξi∗)−i=1∑mriξi−i=1∑mri∗ξi∗+i=1∑mαi(hw,b(xi)−yi−ε−ξi)+
∑ i = 1 m α i ∗ ( y i − h w , b ( x i ) − ε − ξ i ∗ ) \sum_{i=1}^{m}α_i^*(y^i-h_{w,b}(x^i)-ε-ξ_i^*) i=1∑mαi∗(yi−hw,b(xi)−ε−ξi∗)
令函数中对应偏导为0,得到:
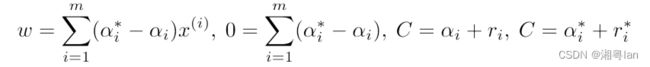
代入到拉格朗日函数中得到之关于 α i α_i αi, α i ∗ α_i^* αi∗的函数,最大化该函数即得到SVR的对偶问题:
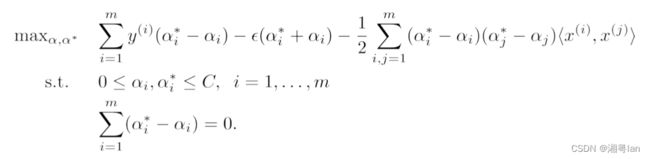
因此可以进行求解,同时对于非线性回归也可引入核函数实现。下面实现SVR。
SVR的实现使用scikit-learn库调用实现,scikit-learn库里集成了大量机器学习的常用方法,其中提供了基于libsvm的SVR解决方案。
任务九 SVR:线性回归实现
#初始化一系列随机样本
np.random.seed(42)
m = 50
X = 2 * np.random.rand(m, 1)
y = (4 + 3 * X + np.random.randn(m, 1)).ravel() # 将多维数组降为一维
#调用sklearn库,实现LinearSVR
from sklearn.svm import LinearSVR
### START THE CODE ###
svr = LinearSVR(C=0.3) #设定epsilon = 0.3,方便观察效果,支持向量均位于容忍区域外侧
svr.fit(X,y) #根据相关文档得到拟合模型
### END THE CODE ###
#找到支持向量
def find_support(svr,X,y):
y_pred=svr.predict(X)#计算预测值
margin=(np.abs(y-y_pred) >= svr.epsilon)#判断是否为支持向量
return np.argwhere(margin)
svr.support_=find_support(svr,X,y)#获取对应的支持向量对应下标,注意将变量名改为你自己的命名
绘制SVR结果
def plot_svr(svr,X,y,axes):
xls=np.linspace(axes[0],axes[1],100).reshape(100,1)
y_pred=svr.predict(xls)
plt.plot(xls, y_pred, "-")
plt.plot(xls, y_pred + svr.epsilon, "--")
plt.plot(xls, y_pred - svr.epsilon, "--")
plt.plot(X, y, "bo")
plt.scatter(X[svr.support_], y[svr.support_], s=180, facecolors='#FFAAAA')
plt.axis(axes)
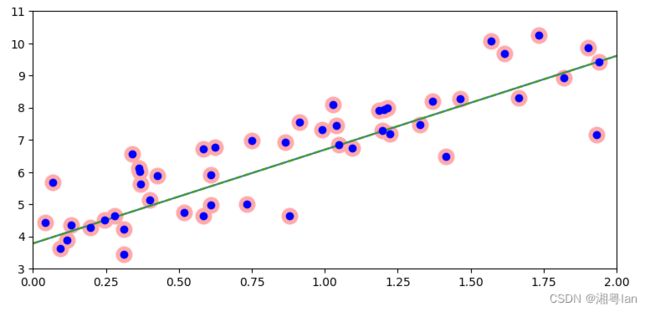
plt.figure(figsize=(9, 4)) # width, height in inches
plot_svr(svr, X, y, [0, 2, 3, 11]) #注意第一个参数改为自己的命名
通过观察图像可以看出,SVR中的支持向量均位于容忍区域外侧
任务十 SVR:非线性回归
非线性回归中,参数C越大,对错样本的惩罚程度越大,正则化项的作用会越小,模型越趋向于过拟合。
反之,C越小,正则化效果越强,模型会更简单。
在实验中同学们可以通过调整C参数观察回归结果的不同。
#初始化随机样本
np.random.seed(42)
m = 100
X = 2 * np.random.rand(m, 1) - 1
y = (0.2 + 0.1 * X + 0.5 * X**2 + np.random.randn(m, 1)/10).ravel()
#实现SVR
from sklearn.svm import SVR
### START THE CODE ###
svr_poly = SVR(kernel='poly',C = 0.3) #对初始化参数C进行调节观察结果
svr_poly.fit(X,y) #拟合模型
### END THE CODE ###
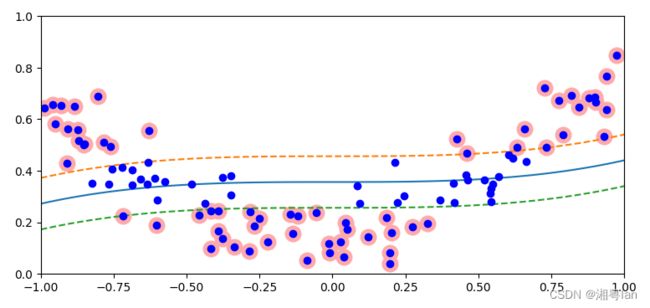
plt.figure(figsize=(9, 4))
plot_svr(svr_poly, X, y, [-1, 1, 0, 1])
对应此数据集,通过改变C参数可以看出C越小,图像弯曲程度越小,而C越大图像越弯曲,对此数据拟合效果越好。