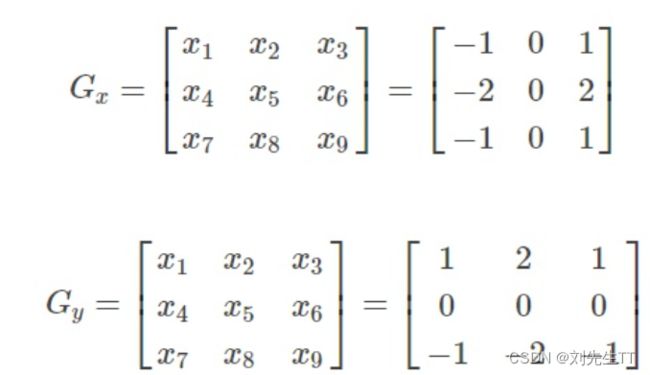NNDL实验六卷积神经网络（2）基础算子

5.2 卷积神经网络的基础算子

卷积神经网络是目前计算机视觉中使用最普遍的模型结构，如图5.8 所示，由$M$个卷积层和$b$个汇聚层组合作用在输入图片上，在网络的最后通常会加入$K$个全连接层。

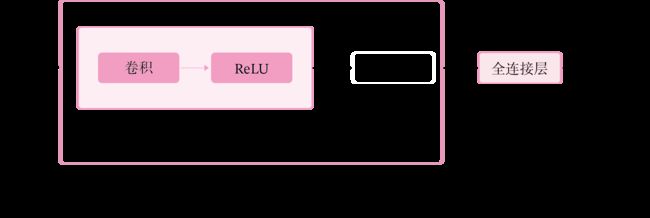
图5.8：卷积神经网络经典结构

从上图可以看出，卷积网络是由多个基础的算子组合而成。下面我们先实现卷积网络的两个基础算子：卷积层算子和汇聚层算子。

5.2.1 卷积算子

卷积层是指用卷积操作来实现神经网络中一层。为了提取不同种类的特征，通常会使用多个卷积核一起进行特征提取。层数越多提取的特征也越来越抽象。

二维卷积提取原理(动图！！！)

拥有多个通道的卷积，例如处理彩色图像时，分别对R, G, B这3个层处理的3通道卷积，如下图：

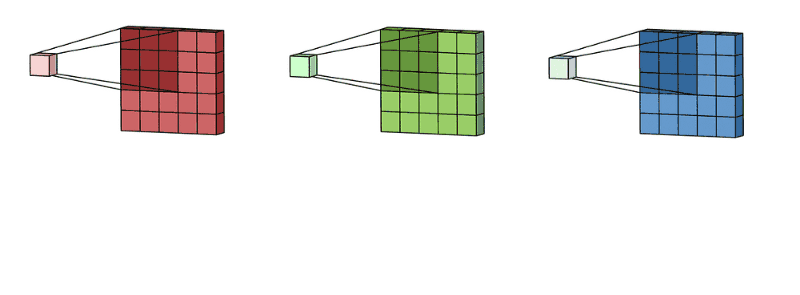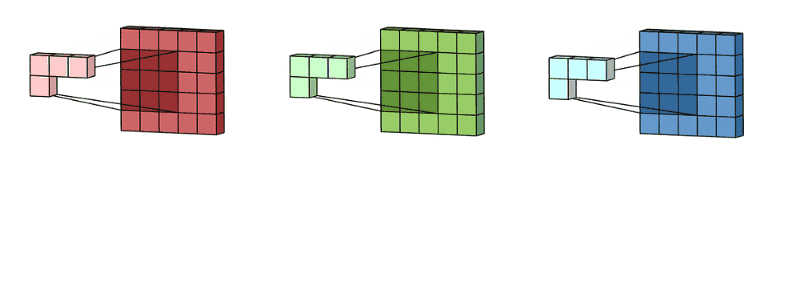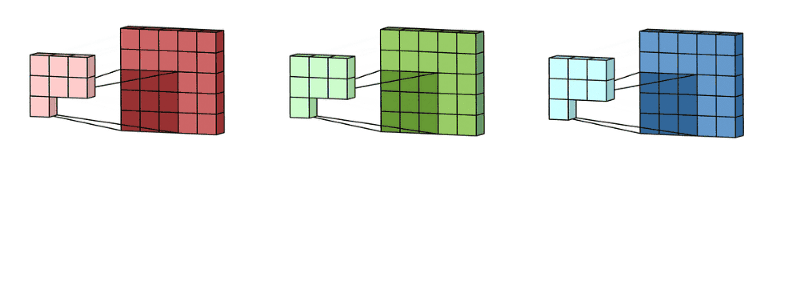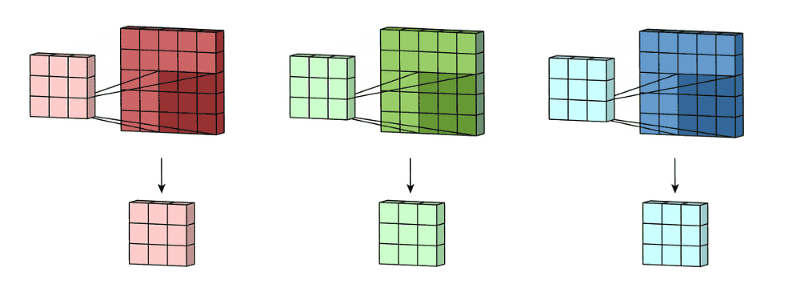
再将三个通道的卷积结果进行合并（一般采用元素相加），得到卷积后的结果，如下图：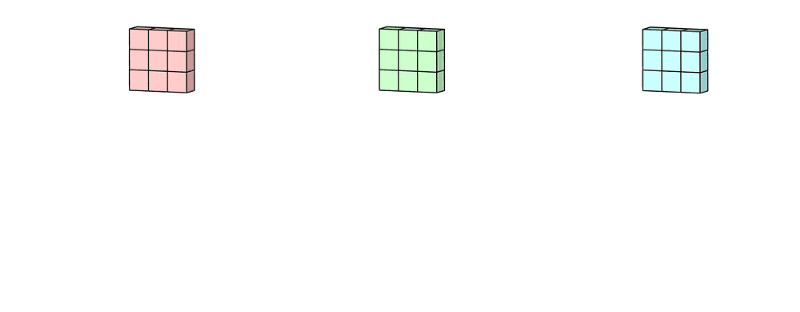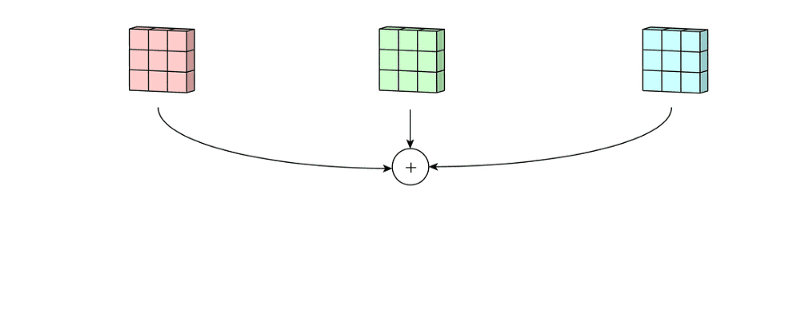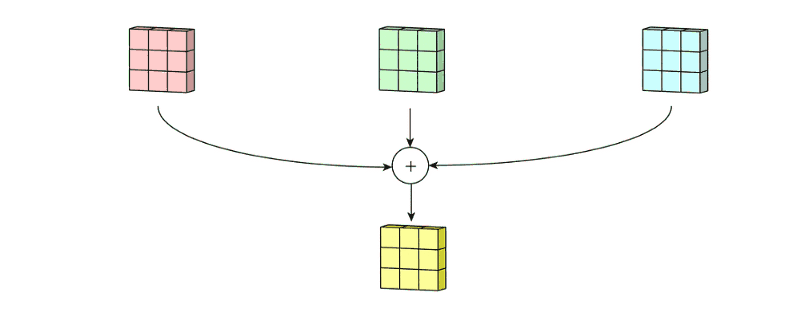

温故而知新——常用的卷积核：

均值滤波：

作用：消除噪点
特点：滤波器中元素之和为1，输出亮度与输入基本一致；均为低通滤波器，主要用于图像模糊/平滑处理、消除噪点；核越大，模糊程度越大；

高斯滤波：

高斯滤波核均值滤波的作用一样，不过高斯滤波内部卷积核的权重不一样，而均值滤波内部的权重是想等的。
特点：滤波器中元素之和为1，输出亮度与输入基本一致；均为低通滤波器，主要用于图像模糊/平滑处理、消除噪点；核越大，模糊程度越大；
高斯滤波器虽然元素总和也为1，但每个位置的权重不一样，权重在行和列上的分布均服从高斯分布，故称高斯滤波器。高斯分布的标准差越大，则模糊程度越大

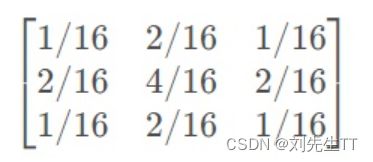
锐化卷积核：

该卷积核就是计算中心位置像素与周围像素的差值，差值越大则表示该元素附近的变化越大，输出值也就越大，因此是高频滤波器的一种。锐化卷积核元素总和如果是0，则有提取图像边缘信息的效果。

sobel算子

提取边界的主要算子。

5.2.1.1 多通道卷积

在前面介绍的二维卷积运算中，卷积的输入数据是二维矩阵。但实际应用中，一幅大小为$M\times N$的图片中的每个像素的特征表示不仅仅只有灰度值的标量，通常有多个特征，可以表示为$D$维的向量，比如RGB三个通道的特征向量。因此，图像上的卷积操作的输入数据通常是一个三维张量，分别对应了图片的高度$M$、宽度$N$和深度$D$，其中深度$D$通常也被称为输入通道数$D$。如果输入是灰度图像，则输入通道数为1；如果输入是彩色图像，分别有$R、G、B$三个通道，则输入通道数为3。

此外，由于具有单个核的卷积每次只能提取一种类型的特征，即输出一张大小为$U\times V$的特征图（Feature Map）。而在实际应用中，我们也希望每一个卷积层能够提取多种不同类型的特征，所以一个卷积层通常会组合多个不同的卷积核来提取特征，经过卷积运算后会输出多张特征图，不同的特征图对应不同类型的特征。输出特征图的个数通常将其称为输出通道数$P$。

---

说明：

《神经网络与深度学习》将Feature Map翻译为“特征映射”，这里翻译为“特征图”。

---

假设一个卷积层的输入特征图$\mathbf{X}\in {\mathbb{R}}^{D\times M\times N}$，其中$(M,N)$为特征图的尺寸，$D$代表通道数；卷积核为$\mathbf{W}\in {\mathbb{R}}^{P\times D\times U\times V}$，其中$(U,V)$为卷积核的尺寸，$D$代表输入通道数，$P$代表输出通道数。

---

说明：

在实践中，根据目前深度学习框架中张量的组织和运算性质，这里特征图的大小为$D\times M\times N$，和《神经网络与深度学习》中$M\times N\times D$的定义并不一致。
相应地，卷积核$W$的大小为${\mathbb{R}}^{P\times D\times U\times V}$。

---

一张输出特征图的计算

对于$D$个输入通道，分别对每个通道的特征图${\mathbf{X}}^d$设计一个二维卷积核${\mathbf{W}}^{p,d}$，并与对应的输入特征图${\mathbf{X}}^d$进行卷积运算，再将得到的$D$个结果进行加和，得到一张输出特征图${\mathbf{Z}}^p$。计算方式如下：

$${\mathbf{Z}}^p=\sum _{d=1}^D{\mathbf{W}}^{p,d}\otimes {\mathbf{X}}^d+b^p，（5.18）$$

$${\mathbf{Y}}^p=f({\mathbf{Z}}^p)。（5.19）$$

其中$p$表示输出特征图的索引编号，${\mathbf{W}}^{p,d}\in {\mathbb{R}}^{U\times V}$为二维卷积核，$b^p$为标量偏置，$f(\cdot )$为非线性激活函数，一般用ReLU函数。

---

说明：

在代码实现时，通常将非线性激活函数放在卷积层算子外部。

---

公式（5.13）对应的可视化如图5.9所示。

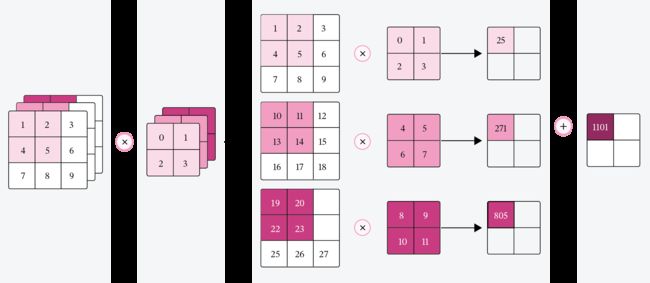
图5.9：多输入通道的卷积运算

多张输出特征图的计算

对于大小为$D\times M\times N$的输入特征图，每一个输出特征图都需要一组大小为$\mathbf{W}\in {\mathbb{R}}^{D\times U\times V}$的卷积核进行卷积运算。使用$P$组卷积核分布进行卷积运算，得到$P$个输出特征图${\mathbf{Y}}^1,{\mathbf{Y}}^2,\cdots ,{\mathbf{Y}}^P$。然后将$P$个输出特征图进行拼接，获得大小为$P\times M^{\prime }\times N^{\prime }$的多通道输出特征图。上面计算方式的可视化如下图5.10所示。

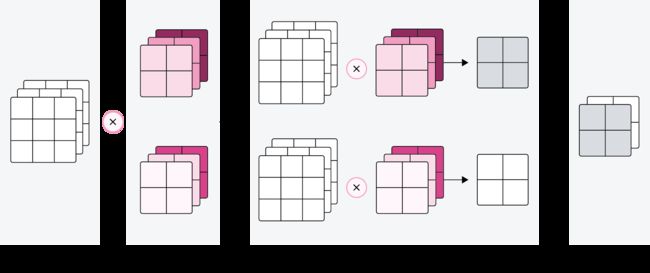
图5.10：多输出通道的卷积运算

5.2.1.2 多通道卷积层算子

根据上面的公式，多通道卷积卷积层的代码实现如下：

import torch.nn as nn
import torch
class Conv2D(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0):
        super(Conv2D, self).__init__()
        # 创建卷积核
        self.weight = nn.Parameter(torch.ones(size=[out_channels, in_channels, kernel_size,kernel_size]))

        self.bias = nn.Parameter(torch.ones(size=[out_channels,1]))
        self.stride = stride
        self.padding = padding
        # 输入通道数
        self.in_channels = in_channels
        # 输出通道数
        self.out_channels = out_channels

    # 基础卷积运算
    def single_forward(self, X, weight):
        # 零填充
        new_X = torch.zeros([X.shape[0], X.shape[1]+2*self.padding, X.shape[2]+2*self.padding])
        new_X[:, self.padding:X.shape[1]+self.padding, self.padding:X.shape[2]+self.padding] = X
        u, v = weight.shape
        output_w = (new_X.shape[1] - u) // self.stride + 1
        output_h = (new_X.shape[2] - v) // self.stride + 1
        output = torch.zeros([X.shape[0], output_w, output_h])
        for i in range(0, output.shape[1]):
            for j in range(0, output.shape[2]):
                output[:, i, j] = torch.sum(
                    new_X[:, self.stride*i:self.stride*i+u, self.stride*j:self.stride*j+v]*weight,
                    axis=[1,2])
        return output

    def forward(self, inputs):
        """
        输入：
            - inputs：输入矩阵，shape=[B, D, M, N]
            - weights：P组二维卷积核，shape=[P, D, U, V]
            - bias：P个偏置，shape=[P, 1]
        """
        feature_maps = []
        # 进行多次多输入通道卷积运算
        p=0
        for w, b in zip(self.weight, self.bias): # P个(w,b),每次计算一个特征图Zp
            multi_outs = []
            # 循环计算每个输入特征图对应的卷积结果
            for i in range(self.in_channels):
                single = self.single_forward(inputs[:,i,:,:], w[i])
                multi_outs.append(single)
                # print("Conv2D in_channels:",self.in_channels,"i:",i,"single:",single.shape)
            # 将所有卷积结果相加
            feature_map = torch.sum(torch.stack(multi_outs), axis=0) + b #Zp
            feature_maps.append(feature_map)
            # print("Conv2D out_channels:",self.out_channels, "p:",p,"feature_map:",feature_map.shape)
            p+=1
        # 将所有Zp进行堆叠
        out = torch.stack(feature_maps, 1)
        return out

inputs = torch.as_tensor([[[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
               [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]]])
conv2d = Conv2D(in_channels=2, out_channels=3, kernel_size=2)
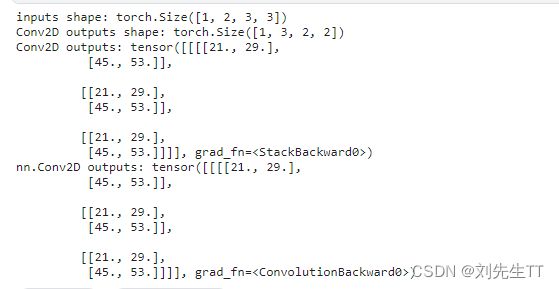
print("inputs shape:",inputs.shape)
outputs = conv2d(inputs)
print("Conv2D outputs shape:",outputs.shape)

# 比较与torch API运算结果
conv2d_torch = nn.Conv2d(in_channels=2, out_channels=3, kernel_size=2)
conv2d_torch.weight.data = nn.Parameter(torch.ones(size=[3, 2, 2, 2]))
conv2d_torch.bias.data = nn.Parameter(torch.ones(size=[3]))
outputs_torch = conv2d_torch(inputs)
# 自定义算子运算结果
print('Conv2D outputs:', outputs)
# torch API运算结果
print('nn.Conv2D outputs:', outputs_torch)

注意！！！这里千万不要网记初始化torch.nn中卷积核的参数

5.2.1.3 卷积算子的参数量和计算量

参数量

对于大小为$D\times M\times N$的输入特征图，使用$P$组大小为$\mathbf{W}\in {\mathbb{R}}^{D\times U\times V}$的卷积核进行卷积运算，参数量计算方式为：

$$parameters=P\times D\times U\times V+P.（5.20）$$

其中，最后的$P$代表偏置个数。例如：输入特征图大小为$3\times 32\times 32$，使用$6$组大小为$3\times 3\times 3$的卷积核进行卷积运算，参数量为：
$$parameters=6\times 3\times 3\times 3+6=168.$$

计算量

对于大小为$D\times M\times N$的输入特征图，使用$P$组大小为$\mathbf{W}\in {\mathbb{R}}^{D\times U\times V}$的卷积核进行卷积运算，计算量计算方式为：

$$FLOPs=M^{\prime }\times N^{\prime }\times P\times D\times U\times V+M^{\prime }\times N^{\prime }\times P。（5.21）$$

其中$M^{\prime }\times N^{\prime }\times P$代表加偏置的计算量，即输出特征图上每个点都要与$P$组卷积核$\mathbf{W}\in {\mathbb{R}}^{D\times U\times V}$进行$U\times V\times D$次乘法运算后再加上偏置。比如对于输入特征图大小为$3\times 32\times 32$，使用$6$组大小为$3\times 3\times 3$的卷积核进行卷积运算，计算量为：

$$FLOPs=M^{\prime }\times N^{\prime }\times P\times D\times U\times V+M^{\prime }\times N^{\prime }\times P=30\times 30\times 3\times 3\times 6\times 3+30\times 30\times 6=151200$$

5.2.2 汇聚层算子

汇聚层的作用是进行特征选择，降低特征数量，从而减少参数数量。由于汇聚之后特征图会变得更小，如果后面连接的是全连接层，可以有效地减小神经元的个数，节省存储空间并提高计算效率。

常用的汇聚方法有两种，分别是：平均汇聚和最大汇聚。

• 平均汇聚：将输入特征图划分为$2\times 2$大小的区域，对每个区域内的神经元活性值取平均值作为这个区域的表示；
• 最大汇聚：使用输入特征图的每个子区域内所有神经元的最大活性值作为这个区域的表示。

图5.11 给出了两种汇聚层的示例。

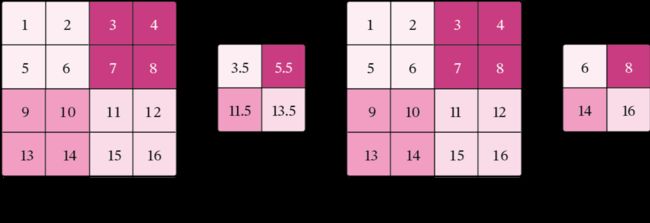
图5.11：汇聚层

汇聚层输出的计算尺寸与卷积层一致，对于一个输入矩阵$\mathbf{X}\in {\mathbb{R}}^{M\times N}$和一个运算区域大小为$U\times V$的汇聚层，步长为$S$，对输入矩阵进行零填充，那么最终输出矩阵大小则为

$$M^{\prime }=\frac{M+2P-U}{S}+1,（5.20）$$
$$N^{\prime }=\frac{N+2P-V}{S}+1.（5.21）$$

由于过大的采样区域会急剧减少神经元的数量，也会造成过多的信息丢失。目前，在卷积神经网络中比较典型的汇聚层是将每个输入特征图划分为$2\times 2$大小的不重叠区域，然后使用最大汇聚的方式进行下采样。

由于汇聚是使用某一位置的相邻输出的总体统计特征代替网络在该位置的输出，所以其好处是当输入数据做出少量平移时，经过汇聚运算后的大多数输出还能保持不变。比如：当识别一张图像是否是人脸时，我们需要知道人脸左边有一只眼睛，右边也有一只眼睛，而不需要知道眼睛的精确位置，这时候通过汇聚某一片区域的像素点来得到总体统计特征会显得很有用。这也就体现了汇聚层的平移不变特性。

汇聚层的参数量和计算量

由于汇聚层中没有参数，所以参数量为$0$；最大汇聚中，没有乘加运算，所以计算量为$0$，而平均汇聚中，输出特征图上每个点都对应了一次求平均运算。

使用飞桨实现一个简单的汇聚层，代码实现如下：

class Pool2D(nn.Module):
    def __init__(self, size=(2, 2), mode='max', stride=1):
        super(Pool2D, self).__init__()
        # 汇聚方式
        self.mode = mode
        self.h, self.w = size
        self.stride = stride

    def forward(self, x):
        output_w = (x.shape[2] - self.w) // self.stride + 1
        output_h = (x.shape[3] - self.h) // self.stride + 1
        output = torch.zeros([x.shape[0], x.shape[1], output_w, output_h])
        # 汇聚
        for i in range(output.shape[2]):
            for j in range(output.shape[3]):
                # 最大汇聚
                if self.mode == 'max':
                    output[:, :, i, j] = torch.max(
                        x[:, :, self.stride * i:self.stride * i + self.w, self.stride * j:self.stride * j + self.h],
                )
                # 平均汇聚
                elif self.mode == 'avg':
                    output[:, :, i, j] = torch.mean(
                        x[:, :, self.stride * i:self.stride * i + self.w, self.stride * j:self.stride * j + self.h],
                )

        return output


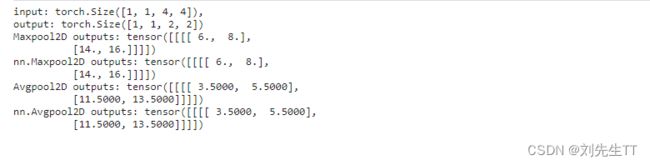
inputs = torch.as_tensor([[[[1., 2., 3., 4.], [5., 6., 7., 8.], [9., 10., 11., 12.], [13., 14., 15., 16.]]]])
pool2d = Pool2D(stride=2)
outputs = pool2d(inputs)
print("input: {}, \noutput: {}".format(inputs.shape, outputs.shape))

# 比较Maxpool2D与torch API运算结果
maxpool2d_torch = nn.MaxPool2d(kernel_size=(2, 2), stride=2)
outputs_torch = maxpool2d_torch(inputs)
# 自定义算子运算结果
print('Maxpool2D outputs:', outputs)
# torch API运算结果
print('nn.Maxpool2D outputs:', outputs_torch)

# 比较Avgpool2D与torch API运算结果
avgpool2d_torch = nn.AvgPool2d(kernel_size=(2, 2), stride=2)
outputs_torch = avgpool2d_torch(inputs)
pool2d = Pool2D(mode='avg', stride=2)
outputs = pool2d(inputs)
# 自定义算子运算结果
print('Avgpool2D outputs:', outputs)
# torch API运算结果
print('nn.Avgpool2D outputs:', outputs_torch)

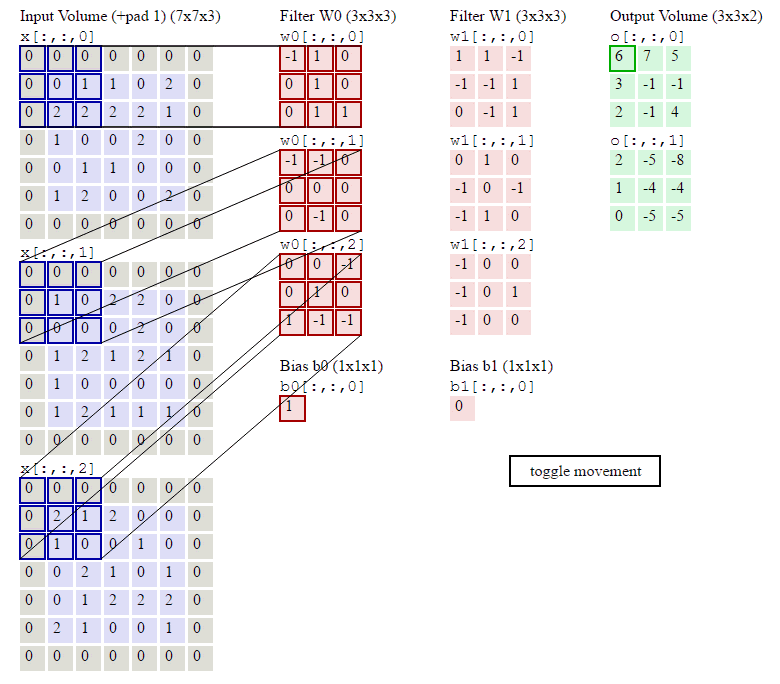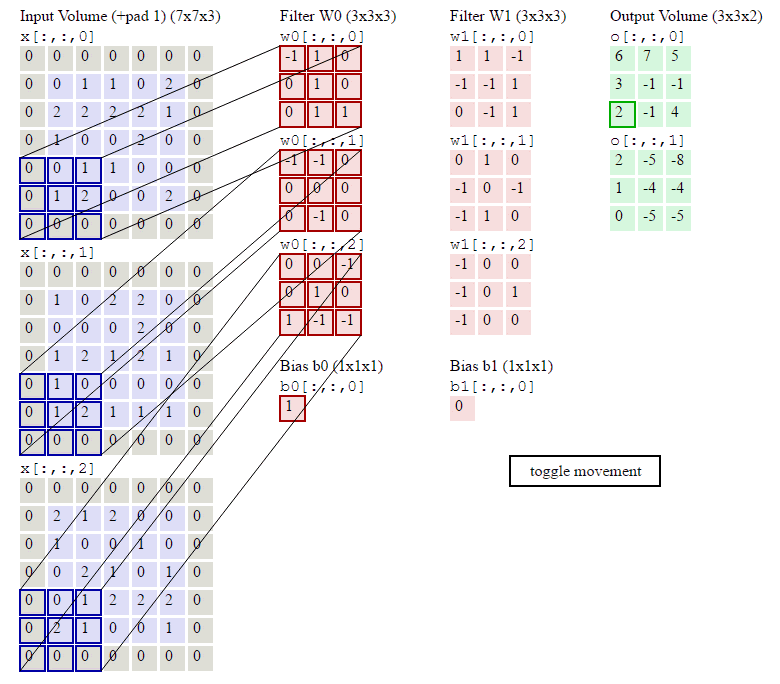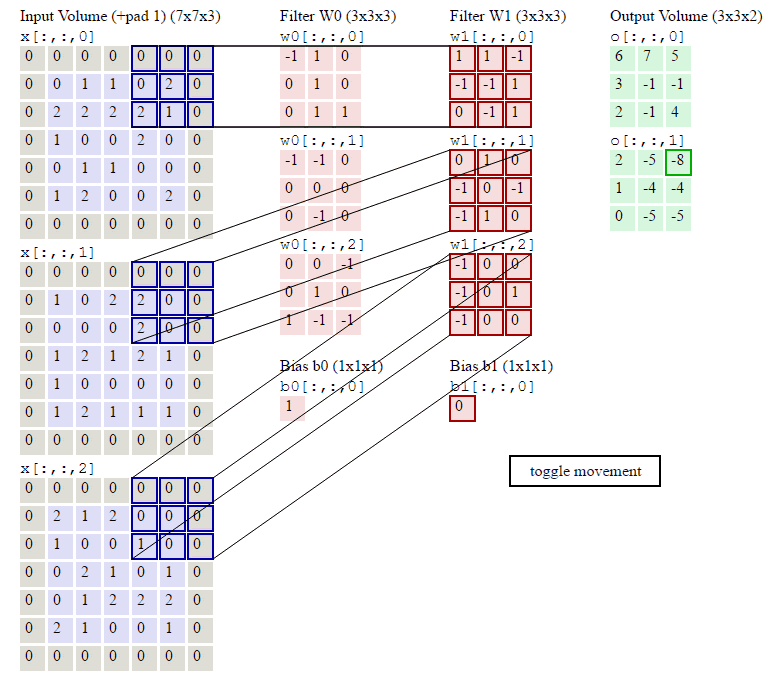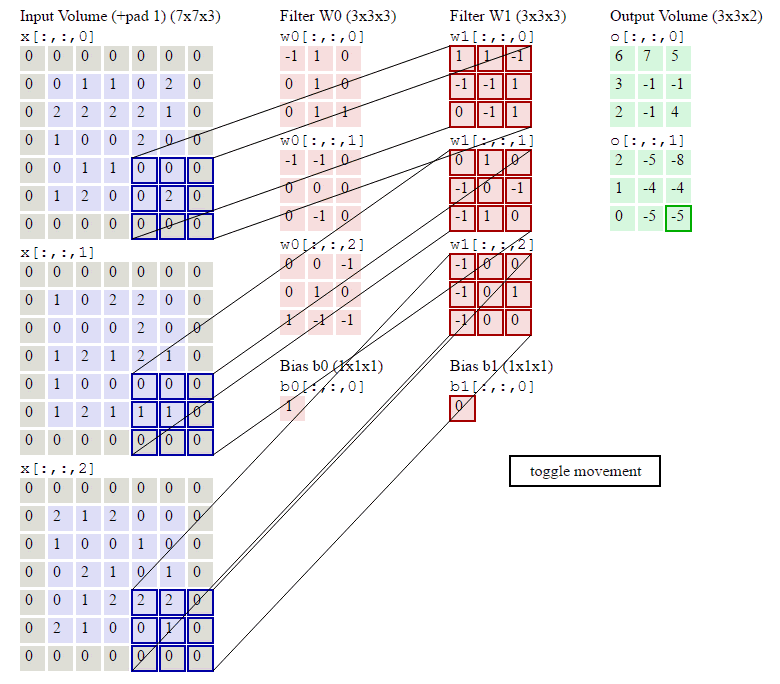
选做题：使用pytorch实现Convolution Demo

翻译如下内容：
Convolutional Neural Networks are very similar to ordinary Neural Networks from the previous chapter: they are made up of neurons that have learnable weights and biases. Each neuron receives some inputs, performs a dot product and optionally follows it with a non-linearity. The whole network still expresses a single differentiable score function: from the raw image pixels on one end to class scores at the other. And they still have a loss function (e.g. SVM/Softmax) on the last (fully-connected) layer and all the tips/tricks we developed for learning regular Neural Networks still apply.

译文：卷积神经网络和之前所讲的普通神经网络十分类似，他们都是由学习权重的神经元组成，每一个神经元接收一些输入，执行点积和激活等操作，整个网络仍旧可以分为每一个微小的得分函数，从一个个小像素到最后的分类数，并且特们也存在一个损失函数（例如SVM\Softmax）在(全链接)最后一层并且我们为常规学习神经网络发展生成的提示仍然使用。

2. 代码实现下图
   

# -*- coding: utf-8 -*-
# @Time : 2022-10-23 19:24
# @Author : Mr.Liu
# @Email : [email protected]
# @File : 3.py
# @ProjectName: python
import torch.nn as nn
import torch

inputs = torch.as_tensor([[[[0,1,1,0,2],
                          [2,2,2,2,1],
                          [1,0,0,2,0],
                          [0,1,1,0,0],
                          [1,2,0,0,2]],
                         [[1,0,2,2,0],
                          [0,0,0,2,0],
                          [1,2,1,2,1],
                          [1,0,0,0,0],
                          [1,2,1,1,1]],
                        [[2,1,2,0,0],
                          [1,0,0,1,0],
                          [0,2,1,0,1],
                          [0,1,2,2,2],
                          [2,1,0,0,1]]
                          ]],dtype=torch.float)
# 比较与torch API运算结果
print(inputs.shape)
conv2d_1 = torch.nn.Conv2d(in_channels=3, out_channels=2, kernel_size=3,padding=1,stride=2)
conv2d_1.weight.data = nn.Parameter(torch.as_tensor([[
                                        [[-1.,1.,0.],
                                         [0.,1.,0.],
                                         [0.,1.,1.]],
                                        [[-1., -1., 0.],
                                         [0., 0., 0.],
                                         [0., -1., 0.]],
                                        [[0.,0.,-1.],
                                         [0.,1.,0.],
                                         [1.,-1.,-1.]]
                                        ],
                                        [[[1.,1.,-1.],
                                         [-1.,-1.,1.],
                                         [0.,-1.,1.]],
                                        [[0., 1., 0.],
                                         [-1., 0., -1.],
                                         [-1., 1., 0.]],
                                        [[-1.,0.,0.],
                                         [-1.,0.,1.],
                                         [-1.,0.,0.]]]]))
conv2d_1.bias.data = nn.Parameter(torch.as_tensor([1,0],dtype=torch.float))
print(conv2d_1.weight.data.shape)
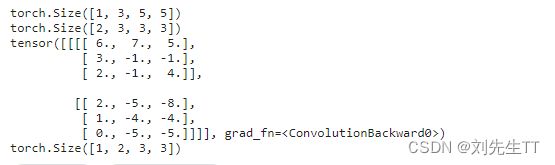
output = conv2d_1(inputs)
print(output)
print(output.shape)

总结:

这次实验练了练习英语，发现英语还没有退步，自己调用pytorch框架卷积了一波，实现了老师给的demo，同时遇到了一些问题，我们可以发现，conv2d的输入和卷积的权重都应该是四维的，其对应意义如下
图片：[输入的图片的数量，输入图片的通道数，每个通道数的高，每个通道数的宽]
卷积核参数初始化：[输出通道数，输入的通道数，每层卷积核的高，每层卷积核宽]。
这算是一个新知识了，有了这个公式以后，卷积就跟做数学题解析几何一样套公式就可以了。
kaggle:https://www.kaggle.com/code/mrliud/notebook5d74a69943

不足：

这次实验没有什么特别不足的地方很满意。除了卷积输入核输出全部需要替换成FLOAT类型。

参考：

NNDL 实验六 卷积神经网络（2）基础算子
[pytorch] TypeError cannot assign torch.FloatTensor as parameter weight
paddlepaddle和torch 对比API
torch,nn初始化权重
常用卷积核小结