MindSpore Reinforcement新特性：分布式训练和蒙特卡洛树搜索

MindSpore Reinforcement

MindSpore Reinforcement v0.5 版本提供了基于Dataflow Fragment的分布式训练能力，通过扩展新的Fragment可以实现灵活的分布式训练策略。在后续的版本迭代中，分布式架构会持续进行迭代优化，并提供全自动的大规模分布式训练支持。此外，v0.5版本还提供了蒙特卡洛树搜索算法的原生支持，通过此算法用户可以实现类似AlphaGo等基于树搜索的强化学习算法。

1、基于Dataflow Fragment的可扩展分布式训练

1.1 背景

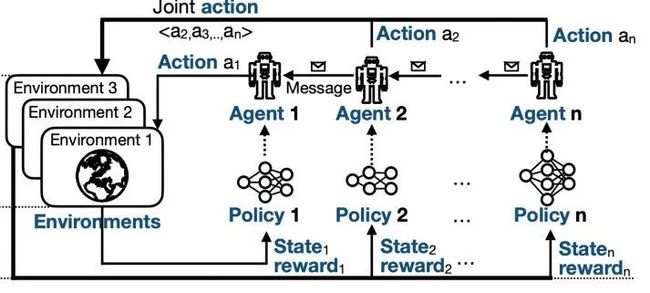
强化学习是一种通过智能体在未知环境中不断地学习如何行动，来解决决策问题的机器学习技术。多智能体的深度强化学习算法需要训练大量存在信息交互的智能体，每个智能体的策略一般由深度神经网络表示。

图1 强化学习流程示意图

强化学习在游戏AI、生物建模、机器人和过程优化等不同领域的现实应用中均取得了显著的成功。然而，这种进步需要依靠大量的计算资源。例如，使用强化学习将多人游戏AI训练到具有人类职业玩家的水平，需要使用大量GPU进行训练。

1.2 当前框架面临的挑战

现有的分布式强化学习平台效率低下。如图2所示，平台通常以一组Python函数的方式来执行给定的强化学习算法(如PPO算法)，这些函数将作为循环中的一部分在训练中被调用。这种方式虽然为用户带来了直观的编程API，但它失去了部分优化的机会，例如，

1）使用Ascend、GPU等硬件加速器来并行部分算法；

2）在多设备上并行执行。

图2 Python函数式执行

1.3 MindSpore Reinforcement提供的思路

MindSpore Reinforcement Learning(下简称MSRL) 采取了不同的方式，将强化学习的算法定义与算法如何并行或分布式执行在硬件设备上进行了解耦。它通过一个新的抽象，即数据流片段图（Fragmented Dataflow Graphs）来实现这一目标，该抽象用于MSRL将算法的不同片段映射到异构设备上，包括Ascend、GPU和多核CPU设备。

算法的每一部分都将成为数据流片段，并由MSRL灵活地分发与并行，如图3所示。

图3 Dataflow Fragment式执行

1.3.1 MSRL的编程模型

在实现以上特性的同时，MSRL仍然为用户保留了直观的编程模型。如图4代码片段为MAPPO算法的实现，用户仍可通过熟悉的算法概念来表达，如actors, learners 和 trainers等。

图4 MSRL的编程模型

因此，MSRL同现有的强化学习框架保持了一定的算法概念兼容性。

1.3.2 MSRL基于Dataflow Fragment的分布式策略

因此，MSRL的一项独特功能是，用户可以轻易地更改强化学习算法的分布式并行策略。MSRL支持不同的分布式策略（DPs），这些策略规定了数据流片段与设备的映射关系。例如，相同的算法可以部署在一台或多台具有单个或多个GPU的计算机或集群上。

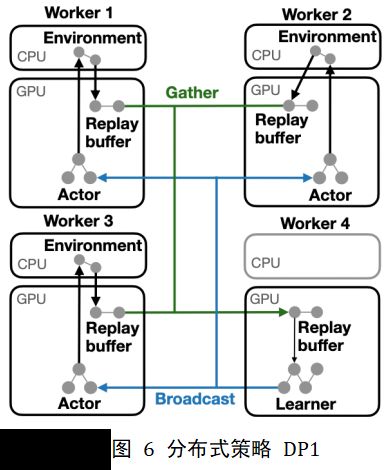
我们通过两个分布式策略示例来说明MSRL对强化学习算法配置的灵活性。图6 DP1将算法划分为三个片段， actor和learner片段映射至不同GPU，environment片段映射至CPU。该策略可以在多个GPU上配置算法，这些GPU可能位于同一台主机，也可能通过网络连接。

图7 DP2对相同算法进行了不同的扩展：它将actor和learner融合为单个GPU片段，并将此融合片段与CPU上的environment片段绑定。如果算法在训练中需要进行数据规约，那么这种类型的部署策略会变的更加有效。现有框架可能需要通过重写部分算法来实现不同的分布式需求，MSRL可以仅通过部署时更改分布式策略来满足这一要求，算法实现不需要进行改动，并且不会牺牲训练性能和扩展性。

1.4 实验

在MSRL使用的静态图模式下，编译器可以通过使用图优化等技术来获得更好的执行性能，有助于规模部署和跨平台运行。实验比较了不同的分布式策略在单/多卡上的训练性能。

如图8所示，我们从单卡扩展到64卡，并在使用上节描述的两种不同的分布式策略验证了PPO的episode训练时间。从结果可知，随着使用的GPU数量的增加，仍能保持不错的加速比。

图8 不同分布式策略在多卡上的训练时间

详情请见：

https://gitee.com/mindspore/reinforcement/tree/master/example/ppo

2、蒙特卡洛树搜索

2.1 背景介绍

两人零和博弈游戏都可以用一棵游戏树来表示整个游戏的过程，若要获得这个博弈中的最佳的步法（动作），传统是利用极小化极大化算法来求解最优解。一些动作空间较小的游戏，如井字棋整棵游戏树的复杂度上界为9!=362880（实际会小于这个值），可以通过现有的计算机算力遍历整棵游戏树来获得最优解，但是对于围棋这一类动作空间巨大的博弈游戏，如围棋的搜索空间达到了3361，现有的计算机算力是根本没有办法通过遍历整棵游戏树来获得最优解的。

图9 围棋游戏树演示

（参考https://www.zhihu.com/question/39916945）

在2006年，研究者提出了基于树结构的蒙特卡洛方法，即蒙特卡洛树搜索（MCTS）。MCTS是一种通过树来表达复杂的组合空间来做决策的搜索算法，每一个树的节点表达环境的一个状态。它以模拟的形式进行随机采样，然后更新节点，在后续的迭代中可以更加准确的做出决策。

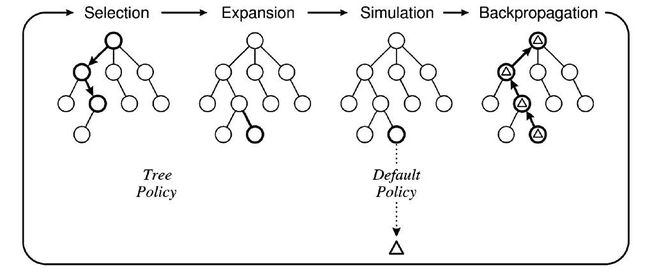
图10 蒙特卡洛树搜索四步示意

（参考C. Browne, et al.,"A Survey of Monte Carlo Tree Search Methods" in IEEE Transactions on Computational Intelligence and AI in Games, vol. 4, no. 01, pp. 1-43, 2012.）

MCTS一般分为四步：

▷ Selection会从当前节点（当前状态）根据提供的选择策略，如Upper Confidence Bounds（UCB），Exploration-Exploitation with Exponential weights（EXP3），Rapid Value Action Estimation（RAVE）等，去选择最优的动作到达子节点（下一个状态）直到叶节点。

▷ Expansion会在Selection到达的叶节点进行扩展除非叶节点是终止节点。扩展的子节点的先验概率（Prior）根据不同算法决定。

▷ Simulation随机选择动作推进游戏的进行，直到达到终止节点。终止节点获得的收益将会用于下一步的更新。

▷ Backpropagation会将Simulation获得的收益以固定策略更新到Selection经过的节点上。

因为MCTS通过随机的对游戏进行推演来构建一棵不对称的搜索树，它大大的减少了搜索空间，并聚焦于更有可能获胜的分支（动作）。通过MCTS构建的AI可以在围棋中达到业余爱好者的水平，但远达不到职业水平。

在2016年，DeepMind将MCTS与深度学习结合起来提出了AlphaGo，战胜了人类最顶尖的围棋玩家。它不仅仅被看做是在围棋上的一个重大突破，也是在AI上的一个重大突破。在AlphaGo中，先验概率的计算和Simulation中的使用到了通过监督学习训练过的神经网络。通过监督学习训练的网络，能更加精确的估计动作的先验概率和评估当前局面。

在以MCTS为基础的强化学习算法的成功之后，越来越多的研究者在强化学习中使用MCTS。

2.2 MindSpore Reinforcement的实现

2.2.1 介绍

MindSpore Reinforcement v0.5.0是原生支持通用MCTS的强化学习框架。现有的强化学习框架普遍采用Python或者动态图来实现MCTS算法，MindSpore Reinforcement使用静态计算图来表达MCTS算法，通过C++实现高效执行。用户可以直接在算法中调用框架内置的MCTS算法，也可以通过扩展来完成自定义逻辑。

2.2.2 使用方法

图11 MindSpore Reinforcement MCTS API使用展示

在框架提供的接口中，用户只需要创建指定类型的蒙特卡洛树，然后调用mcts_search方法就能执行MCTS算法中的四步并获取最优的动作。

2.2.3 MindSpore Reinforcement的方案

框架首先会通过MindSpore算子在C++侧创建一棵指定类型的蒙特卡洛树，后续的操作都会被应用在这棵树上。

Selection和Backpropagation操作在Python侧是以MindSpore算子的形式呈现出来的，实际会调用C++侧定义的选择策略和更新策略，去修改之前定义的树。动作的先验概率和Simulation的方法在Python侧被定义和实现，它们分别被作为Expansion和Backpropagation的输入去修改之前定义的树。

图12 MindSpore Reinforcement MCTS 结构

2.2.4 算法逻辑的扩展

MindSpore Reinforcement当前版本提供了传统的MCTS。由于MCTS发展速度迅速，不同的算法选择动作的策略和计算先验概率的方法也不同。当框架内置的MCTS算法不能满足用户要求时，框架提供了MCTS算法逻辑注入的能力，来满足用户对MCTS变种算法的需求。

如图12所展示，如何选择子节点以及如何更新节点是在计算图中被调用的，用户需要以自定义算子的形式继承框架提供的基类并重写虚函数。自定义选择策略和更新策略可以满足不同MCTS算法，如背景章节提到的UCB，EXP3等方法。

如上文所说不同的算法计算先验概率的方法也不同，如AlphaGo就使用了神经网络，而普通MCTS则使用了平均概率，所以我们提供用户可以在Python层定义先验概率的计算和Simulation的方式。这两个模块的自定义使得MCTS框架有了足够的泛化能力。

MCTS的示例请见：

https://gitee.com/mindspore/reinforcement/tree/master/example/mcts

MCTS的接口使用与介绍请见：

https://gitee.com/mindspore/reinforcement/blob/master/mindspore_rl/utils/mcts/mcts.py