蒙特卡洛树、井字棋
文章目录
-
- 一、算法概括:
- 二、算法实现步骤总结:
- 三、算法源码
- 五、算法总结
- 引用:
一、算法概括:
蒙特卡罗树搜索是一种基于树数据结构、能权衡探索与利用、在搜索空间巨大仍然比较有效的的搜索算法。UCB(Upper Confidence Bounds)算法。就是在选择子节点的时候优先考虑没有探索过的。如果都探索过就根据得分来选择,得分不仅与平均回报有关而且与被选中的次数有关:也就是说这个子节点如果平均得分高就约有可能选中(平均分高赢得可能性更大),同时如果子节点选中次数较多则下次不太会选中(访问次数更少的有优势)。因此MCTS根据配置探索和利用不同的权重,可以实现比随机或者其他策略更有启发式的方法。
二、算法实现步骤总结:
- 第一步是Selection,一般是先选择未被探索的子节点,如果都探索过就选择UCB值最大的子节点。
- 第二步Expand,就是在前面选中的子节点中走一步创建一个新的子节点,随机访问一个孩子节点。
- 第三步是Simulate,就是在前面新Expand出来的节点开始模拟下棋,直到到达游戏结束状态,这样可以收到到这个Expand出来的节点的得分是多少。
- 第四步是Backpropagate,把前面Simulate出来的节点得分反馈到前面所有父节点中,更新这些节点的访问次数和胜率。方便后面计算UCB值。
三、算法源码
# -*- coding: utf-8 -*-
"""
Created on Mon Nov 12 19:55:03 2018
@author: duxiaoqin
Functions:
(1) MCTS Algorithm for TicTacToe
"""
from graphics import *
from tictactoe import *
from tttdraw import *
from tttinput import *
import sys
import time
import math
from random import *
class NodeInfo:
def __init__(self):
self.player = None
self.visit = 0
self.win = 0
def MCTS(root, nodes_map):
def Select(node):
node_key=node.ToString()
path.append(node_key)
node_info=nodes_map.get(node_key)
if node_info==None:
node_info=NodeInfo()
node_info.player=node.getPlayer()
nodes_map[node_key]=node_info
while isFullyExpanded(node):
if node.isGameOver()!=None:
return node
node=BestUCTChild(node)
child_key=node.ToString()
path.append(child_key)
child_info=nodes_map.get(child_key)
if child_info==None:
child_info=NodeInfo()
child_info.player=node.getPlayer()
nodes_map[child_key]=child_info
return node#如果是最终节点直接返回
def Expand(node):
node_key=node.ToString()
node_info=nodes_map.get(node_key)
path.append(node_key)
if node_info==None:
node_info=NodeInfo()
node_info.player=node.getPlayer()
nodes_map[node_key]=node_info
if node.isGameOver()==None:
node=RandomUnvisitedChild(node)
child_key=node.ToString()
path.append(child_key)
child_info=nodes_map.get(child_key)
if child_info==None:
child_info=NodeInfo()
child_info.player=node.getPlayer()
nodes_map[child_key]=child_info
return node
else :
return node
def Simulate(node):#根据Expand返回的节点开始模拟下棋
result = node.isGameOver()
while result == None:#直到游戏结束时才退出循环
node = RandomChild(node)
result = node.isGameOver()
return result#返回游戏结束的结果
def Backpropagate(result):
for node_key in path:
UpdateStatistics(node_key, result)
def MaxVisitChild(node):#访问次数最多的节点
max_visit_num = -sys.maxsize
max_visit_child = ()
moves = node.getAllMoves()
for move in moves:
tmp_node = node.clone()
tmp_node.play(*move)
child_info = nodes_map.get(tmp_node.ToString())
if child_info == None:
continue
if max_visit_num < child_info.visit:
max_visit_num = child_info.visit
max_visit_child = move
return max_visit_child
def isFullyExpanded(node):#判断是否完全Expanded
moves = node.getAllMoves()
for move in moves:
tmp_node = node.clone()
tmp_node.play(*move)
child_info = nodes_map.get(tmp_node.ToString())#对于其所有的孩子节点在nodes_map中进行查询
if child_info == None:#没有找到孩子节点的信息,说明没有FullyExpanded
return False
return True
def BestUCTChild(node):
c = 1.4142135623730951
best_uct = -sys.maxsize#以下三项为记录最好的孩子节点做准备
best_uct_child = None
node_info = nodes_map[node.ToString()]
moves = node.getAllMoves()#对其所有的孩子节点通过ucb算法进行评估,
for move in moves:
tmp_node = node.clone()
tmp_node.play(*move)
child_key = tmp_node.ToString()
child_info = nodes_map[child_key]
ucb1 = child_info.win / child_info.visit + \
c * math.sqrt(math.log(node_info.visit) / child_info.visit)
if best_uct < ucb1:
best_uct = ucb1
best_uct_child = move
if best_uct_child != None:#在确定找到最好的节点,node转变为最好的节点返回
node.play(*best_uct_child)
return node#返回可能1.node的孩子节点中最好的。2.node节点本身(当node是终止节点时)
def RandomChild(node):
moves = node.getAllMoves()
node.play(*moves[randint(0, len(moves) - 1)])#随机在孩子节点中选取一个执行下棋
return node#返回孩子节点
def RandomUnvisitedChild(node):#随机选取一个没有访问的子节点。
moves = node.getAllMoves()
while True:
tmp_node = node.clone()
move = moves[randint(0, len(moves) - 1)]
tmp_node.play(*move)
child_info = nodes_map.get(tmp_node.ToString())
if child_info == None:
return tmp_node
def UpdateStatistics(node_key, result):#更新node_key节点的数据
node_info = nodes_map[node_key]
node_info.visit += 1
if node_info.player == TicTacToe.BLACK:#
if result == -1:
node_info.win += 1
elif result == 0:
node_info.win += 0.5
else:
if result == 1:
node_info.win += 1
elif result == 0:
node_info.win += 0.5
decision_time = 500
for time in range(decision_time):
node = root.clone()
path = []
node = Select(node)
simulation_node = Expand(node)
simulation_result = Simulate(simulation_node)
Backpropagate(simulation_result)
return MaxVisitChild(root)
def main():
win = GraphWin('MCTS for TicTacToe', 600, 600, autoflush=False)
ttt = TicTacToe()
tttdraw = TTTDraw(win)
tttinput = TTTInput(win)
tttdraw.draw(ttt)
nodes_map = {}
while win.checkKey() != 'Escape':
if ttt.getPlayer() == TicTacToe.WHITE:
move = MCTS(ttt, nodes_map)
if move != ():
ttt.play(*move)
tttinput.input(ttt)
tttdraw.draw(ttt)
if ttt.isGameOver() != None:
time.sleep(1)
ttt.reset()
tttdraw.draw(ttt)
#win.getMouse()
win.close()
if __name__ == '__main__':
main()
五、算法总结
该算法平衡了节点选取中的利用与探索问题。我觉得主要体现在select中,对于已有信息的节点(被完全扩展的节点),选取ucb值最大的进行访问,而对于没有访问的(没被完全扩展的节点)节点,则通过模拟进行探索,将探索的结果反馈回去将数据进行更新。对于后面的expand以及simulate就是完成模拟,然后Backpropagate将数据进行更新。 UCB1 算法在利用与探索之间也取得了某种折中。
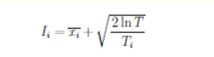
当拉杆i 的平均回报较大时,UCB1 值较大,每次选择时拉杆i 有较大的优势;当拉杆i 被选中的次数较少时,第2 项比较大,UCB1 值也较大,每次选择时拉杆i 也有较大的优势。
引用:
武汉纺织大学杜老师的github
此文章在学完杜小勤的课程后所写,文章中部分内容是借鉴杜老师。
