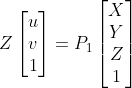三角测量及在SLAM中的使用

目录

1. 前言

2. 三角测量的定义

3. 三角测量的推导

4. 三角测量对应的代码

---

这篇文章主要参考《SLAM十四讲》和《多视觉几何》两本书关于三角测量的原理和推导内容，以ORBSLAM2和ORBSLAM3为例，说一下三角测量的应用，有不对的地方，欢迎指正交流～～

1. 前言

以单目初始化为例，得到两张图像的匹配点之后，第一步就是计算H矩阵或者F矩阵，并从这两个矩阵中恢复出这两帧之间相机的运动，也就是R，t 

有了相机的位姿，接下来就是恢复3D点，即通过两帧图像中对应的匹配点的像素坐标x1,x1'和相机的位姿R，t，计算得到其对应的在三维世界中的坐标X；

这里要和PnP做一下区分，PnP也是两帧图像，但是其中一帧的3D点X1, X2, X3已知，则通过这些3D点以及对应的另一帧的2D坐标(x1,x2,x3)，来估计两帧的运动R，t;

当然，也需要和对极几何做一个区分，对极几何是仅仅通过两张图像的匹配点像素坐标(x1,x1')...(x8,x8')，就可以计算出两帧图像的相对运动R，t；

因此在ORBSLAM中这三种方法的顺序是：
1. 由两张图像的匹配点，利用对极几何计算出H或者F矩阵，并从这两个矩阵中恢复出R，t

2. 有了R,t 就可以利用相机的位姿和两帧对应的像素坐标用三角测量计算出其对应的3D点坐标

至此，相机的位姿和对应的地图点就都有了，接下来正常跟踪即可；

3. 跟踪丢失后，就需要回到原来机器人曾经经过的位置找匹配帧，找到的匹配帧是有其3D地图点和位姿的，用这些3D点和当前帧自己的像素坐标， PnP计算出当前帧相较于匹配帧的运动R，t

2. 三角测量的定义

今天主要说一下三角测量。我们说对极几何是基于两帧图像匹配很准确的情况，但是在实际的匹配中，如ORB的匹配，点的像素坐标的误差也可能是比较大的，也就是被测量点x和x‘ 有误差，这就导致了反向投影点可能是不共面的。也就意味着不存在空间点X很精确的满足两帧之间的投影关系,或者说不存在点X同时满足下面这两个式子：

                                                                       

如下图所示：

从非理想点x和x’ 反投影回去的射线在三维空间中不共面

 

那么这时候的任务就变成，如何找出一个精确满足所给定的几何关系的3D点, 满足下面的式子：
                                                      

即通过来计算。

《多视觉几何》中说到，这样的三角测量法是具有射影不变的，因为他仅仅最小化了图像距离，且都不依赖与定义所使用的摄影坐标系，即不同的射影重构将投影到相同的点； 这里的理解是投影点其实是与外界坐标系无关的，利用三角化恢复出的三维点，只与两帧之间的外参Rt有关，这点通过P矩阵也能看出来；这一点在后面的代码中会看得更清楚一点；

3. 三角测量的推导

三角测量的前提是相机的内参K已知，且两帧之间的外参R，t也已知，并且这些矩阵都比较准确，或者相对于匹配点的像素误差来讲，相对准确。那么就可以有下面的式子：

                                    

                                                                  

以x1'为例进行推导，首先，式展开后其实是

                                             

z其实就代表了实际地图点深度；

先用叉乘消去尺度因子Z, 即 

 

向量叉乘公式如下：，　则对应可以得到式子：

                         

这三个方程其实是线性相关的，从其中可以总结出两个式子，再加上和的映射关系，可以得到下面四个式子：

                       

这就可以转换成其次方程，其中

                    

转换成齐次方程之后，就可以利用齐次解的方法，也就是取A的最小奇异值对应的单位奇异向量作为解；

4. 三角测量对应的代码

有了上面的理论推导后，就可以来看一下三角测量在SLAM中的应用，这里还是简单一点，以ORBSLAM2为例，假设初始化时相机对应的是近似平面的场景，这时使用H矩阵进行推到；

1. FindHomography() 函数利用两帧图像中的匹配点计算出两张图像对应的单应变换矩阵H;

2. ReconstructH() 函数从H矩阵中恢复出R,t，并对Rt进行验证和取舍

3. CheckRT3D() 利用匹配点对R,t进行验证，具体方法为保证像素点的恢复出的3D点的重投影误差在合理范围内

4. 在CheckRT3D()中会先构建投影矩阵P1，P2，然后依次取出众多匹配点中的一对儿点进行三角化

在ORBSLAM2中三角化对应的代码为：

/**
 * @brief 给定投影矩阵P1,P2和图像上的点kp1,kp2，从而恢复3D坐标
 *
 * @param kp1 特征点, in reference frame
 * @param kp2 特征点, in current frame
 * @param P1  投影矩阵P1
 * @param P2  投影矩阵P２
 * @param x3D 三维点
 * @see       Multiple View Geometry in Computer Vision - 12.2 Linear triangulation methods p312
 */
void Initializer::Triangulate(const cv::KeyPoint &kp1, const cv::KeyPoint &kp2, const cv::Mat &P1, const cv::Mat &P2, cv::Mat &x3D)
{
    cv::Mat A(4,4,CV_32F);

    A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0);
    A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1);
    A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0);
    A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1);

    cv::Mat u,w,vt;
    cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);
    x3D = vt.row(3).t();
    x3D = x3D.rowRange(0,3)/x3D.at(3);
}

好了，以上就是三角化对应的理论和代码，欢迎交流指正～～ 

如有疑问,欢迎交流: wx: baobaohaha_ 欢迎对SLAM有兴趣的小伙伴一起交流学习~~