径向基函数神经网络（RBFNN）的权值更新策略Python实现

本文将稍微介绍径向基函数的基础知识，之后以鸢尾花数据集为例，介绍三种RBFNN的权值更新方法（激活函数使用高斯函数），即：直接计算法，自组织选取法，有监督学习（梯度下降法），确定RBFNN的三部分权重（高斯函数的中心和宽度，隐藏层与输出层之间的链接权）。

鸢尾花数据集

https://archive.ics.uci.edu/ml/index.php
可从此处下载一些常用的简单的机器学习数据集，本文使用的鸢尾花数据集（将在最后的网盘链接中给出）包含三类，共150个样本，每条样本有4个属性，以csv文件的方式存储。

共有“Iris-setosa”、“Iris-versicolor”、“Iris-virginica”这三种不同的鸢尾花种类。我们的任务就是，通过训练集中的样本，建立一个能够解决鸢尾花三分类问题的径向基函数神经网络模型。
首先，利用pandas读入数据，划分测试集和训练集。利用sklearn中的shuffle方法随机打乱数据后，取前130个样本作为训练集，后20个作为测试集。

def loadData(filename):
    data = np.array(pd.read_csv(filename,header=None).values)
    lab=["Iris-setosa","Iris-versicolor","Iris-virginica"]
    for i in range(len(data)):
        for j in range(len(lab)):
            if data[i][-1]==lab[j]:
                data[i][-1]=j
    data=shuffle(data)#打乱样本数据
    for i in range(4):#归一化
        data[:,i]=(data[:,i]-np.min(data[:,i]))/(np.max(data[:,i])-np.min(data[:,i]))
    train=np.array(data[:-20])
    test=np.array(data[-20:])
    return train,test

径向基函数神经网络

RBFNN的结构示意图：
高斯函数：

径向基函数神经网络的结构，与常规的BP网络的结构类似（看起来长得很像），不同的是，BP网络的激活函数是一个确定的函数，不含有待估参数，且其各层间的链接权都需要更新。而RBF网络输入层与隐藏层之间的链接权恒为1，不需要更新；隐藏层与输出层之间的链接权（权值矩阵）需要更新；隐藏层的节点，每个节点对应一个不同的激活函数（高斯函数的中心和方差不同），其方差和中心以矩阵形式表示，也需要确定。
假设，我们要建立一个输入层有m个节点(与输入向量的维数相同)，隐藏层有P个节点，输出层有n个节点(与待分类样本的类别数相同)，选用高斯函数作为激活函数的径向基函数神经网络。则网络中存在P个高斯函数，我们也就需要确定P个中心(记为c)，P个宽度(也就是方差，记为b)，则c应该是一个维数为Pm的矩阵，b为维数为Pn的矩阵，隐藏层与输出层之间的链接权记为w，为一个P*n的矩阵。我们学习的目标就是确定一组c，b，w，使得模型能够对输入的样本确定其所属类别。

一、直接计算法

该方法好像有点极限学习机的意思。假设隐藏层每个节点所对应的激活函数的权值已知，也就是事先确定了一组c和b，只需再确定隐藏层与输出层的链接权w即可。
我们随即初始化一组c，b，那么对于每一个样本其在隐藏层的输出也就确定了。我们希望模型（在训练集上的）的输出能够跟期望输出一致，我们知道网络的实际输出其实是隐藏层的输出向量（记为hidOut）与权值矩阵w的乘积，那么网络的预测值out=hidOutw，我们希望预测值out能与标签值T相同，也就是说w可由线性方程组hidOutw=T求出（w=inv(hidOut)*T），那么只要表示出隐藏层的输出矩阵hidOut，和标签矩阵T，之后令hidOut的伪逆矩阵与T做矩阵乘法即可，其结果就是我们确定的w。
对于高斯函数的参数，继续使用一开始的时候随机初始化的那些值就可以，到这里，网络中的待估参数就都确定出来了，即可进行预测了。
1.初始化权值c，b

def init(inputnum,hiddennum,outnum):
    c=np.random.normal(0.0, 1, (hiddennum, inputnum))
    b=np.random.normal(0.0, 1, (hiddennum, 1))
    return c,b

2.记录样本所对应的隐藏层输出和标签向量
计算隐藏层的输出结果：

def f(x,c,b):
    x=c-x
    X=[]
    for i in range(len(x)):
        X.append(-sum(x[i]*x[i])/(b[i]*b[i]))
    X=np.mat(X)
    return np.exp(X)

记录样本所对应的隐藏层输出和标签向量

	ho=[]
    T=[]
    for i in train:
        x=i[:-1]
        ho.append(f(x,c,b))
        lab=np.zeros(3)
        lab[i[-1]]+=1
        T.append(lab)
    T=np.array(T)
    ho=np.array(ho)
    ho=ho.reshape(130,10)

3.计算伪逆矩阵，确定权值矩阵w
利用numpy.linalg.pinv()得到矩阵的伪逆，之后用伪逆与T相乘得到w

	hopiv=np.linalg.pinv(ho)
    w=np.dot(hopiv,T)
    w=w.T

4.对模型进行测试

#测试
    ans=[]
    for i in test:
        x=i[:-1]
        hout=f(x,c,b)
        out=np.dot(w,hout)
        if np.argmax(out)==i[-1]:
            ans.append(1)
        else:
            ans.append(0)
    print(sum(ans)/len(ans))

经过测试发现，我们所确定的模型，在测试集上有良好的表现，其准确率基本能保持在80%~100%，说明我们的方法是行之有效的。
测试十次，每次在不同测试集上的准确率如图所示。

参考代码如下：

import pandas as pd 
import numpy as np 
from sklearn.utils import shuffle
import matplotlib.pyplot as plt
def loadData(filename):
    data = np.array(pd.read_csv(filename,header=None).values)
    lab=["Iris-setosa","Iris-versicolor","Iris-virginica"]
    for i in range(len(data)):
        for j in range(len(lab)):
            if data[i][-1]==lab[j]:
                data[i][-1]=j
    data=shuffle(data)
    for i in range(4):
        data[:,i]=(data[:,i]-np.min(data[:,i]))/(np.max(data[:,i])-np.min(data[:,i]))
    train=np.array(data[:-20])
    test=np.array(data[-20:])
    return train,test
#建立一个4个输入节点，3个输出节点，10个隐藏节点的RBFNN
def init(inputnum,hiddennum,outnum):
    c=np.random.normal(0.0, 1, (hiddennum, inputnum))
    b=np.random.normal(0.0, 1, (hiddennum, 1))
    return c,b
def f(x,c,b):
    x=c-x
    X=[]
    for i in range(len(x)):
        X.append(-sum(x[i]*x[i])/(b[i]*b[i]))
    X=np.mat(X)
    return np.exp(X)
def Train():
    c,b=init(4,10,3)
    train,test=loadData("iris.csv")
    ho=[]
    T=[]
    for i in train:
        x=i[:-1]
        ho.append(f(x,c,b))
        lab=np.zeros(3)
        lab[i[-1]]+=1
        T.append(lab)
    T=np.array(T)
    ho=np.array(ho)
    ho=ho.reshape(130,10)
    hopiv=np.linalg.pinv(ho)
    w=np.dot(hopiv,T)
    w=w.T
    #测试
    ans=[]
    for i in test:
        x=i[:-1]
        hout=f(x,c,b)
        out=np.dot(w,hout)
        if np.argmax(out)==i[-1]:
            ans.append(1)
        else:
            ans.append(0)
    print(sum(ans)/len(ans))
    return sum(ans)/len(ans)

def main():
    acc=[]
    for i in range(10):
        acc.append(Train())
    plt.bar(range(len(acc)),acc)
    plt.show()
    pass
main()

二、自组织选取中心学习法
该方法与直接计算法的思想和步骤类似，只不过直接计算法是随机生成的P个高斯函数的中心和方差，而自组织选取是先通过聚类的方法，将训练集聚成P类，从而确定P个聚类中心，之后通过聚类中心再计算出P个方差，以此来确定隐藏层P个激活函数的参数，之后的步骤与直接计算法相同。
1.利用K-means确定P个聚类中心

def KNN(data,train_num=120,num=10,Flag=0.1):
    Center = [] #质心索引
    center = [] #质心数据
    result = np.full(train_num,-1)
    #防止初始化质心时重复
    def There_is_no(a):
        for i in Center:
            if a == i:
                return False
        return True
    #随机选定num个初始质心,坐标保存到center中
    i=0
    while i<num:
        a = random.randint(0,train_num-1)
        if There_is_no(a):
            Center.append(a)
            i+=1
    for i in range(len(Center)):
        center.append(data[Center[i]])
        result[Center[i]]=i
    T=0
    rz_=0
    while True:
        T+=1
        #计算每一个样本的类别
        for i in range(train_num):
            flag = 0
            min = float("inf")
            for j in range(len(center)):
                L = np.sqrt(np.sum((data[i]-center[j])**2))#欧氏距离
                if min > L:
                    min = L
                    flag = j
            result[i] = flag
        #每一类样本重新计算质心：
        center_=np.array(result)
        rz=0
        for i in range(num):
            a = np.zeros(len(data[0]))
            count = 0
            for j in range(train_num):
                if result[j] == i:
                    count+=1
                    a=np.add(a,data[j])
            center[i]=a/count
            rz+= np.sqrt(np.sum((center[i]-center_[i])**2))
        if abs(rz-rz_)<Flag:
            break
        rz_=rz
    return Center

2.重写直接计算法的init()方法

def init(inputnum,hiddennum,outnum,cIndex,Data):
    c=[]
    for i in cIndex:
        c.append(Data[i])
    c=np.array(c)
    b=[]
    for k in range(hiddennum):
        t=[]
        for i in range(len(c)):
            for j in range(len(c)):
                t.append(np.linalg.norm(c[i]-c[j],2))
        b.append([sum(t)/hiddennum])
    b=np.array(b)
    return c,b

之后的思路和步骤基本就与直接计算法相同了。
同样记录十次模型的准确率，如下图所示，能够看出其效果较直接计算法有较大提升。

参考代码：

import numpy as np
import random
from sklearn.utils import shuffle
import pandas as pd 
import matplotlib.pyplot as plt
def KNN(data,train_num=120,num=10,Flag=0.1):
    Center = [] #质心索引
    center = [] #质心数据
    result = np.full(train_num,-1)
    #防止初始化质心时重复
    def There_is_no(a):
        for i in Center:
            if a == i:
                return False
        return True
    #随机选定num个初始质心,坐标保存到center中
    i=0
    while i<num:
        a = random.randint(0,train_num-1)
        if There_is_no(a):
            Center.append(a)
            i+=1
    for i in range(len(Center)):
        center.append(data[Center[i]])
        result[Center[i]]=i
    T=0
    rz_=0
    while True:
        T+=1
        #计算每一个样本的类别
        for i in range(train_num):
            flag = 0
            min = float("inf")
            for j in range(len(center)):
                L = np.sqrt(np.sum((data[i]-center[j])**2))#欧氏距离
                if min > L:
                    min = L
                    flag = j
            result[i] = flag
        #每一类样本重新计算质心：
        center_=np.array(result)
        rz=0
        for i in range(num):
            a = np.zeros(len(data[0]))
            count = 0
            for j in range(train_num):
                if result[j] == i:
                    count+=1
                    a=np.add(a,data[j])
            center[i]=a/count
            rz+= np.sqrt(np.sum((center[i]-center_[i])**2))
        if abs(rz-rz_)<Flag:
            break
        rz_=rz
    return Center
def loadData(filename):
    fp = open(filename)
    data = np.array(pd.read_csv(filename,header=None).values)
    lab=["Iris-setosa","Iris-versicolor","Iris-virginica"]
    for i in range(len(data)):
        for j in range(3):
            if data[i][-1]==lab[j]:
                data[i][-1]=j
    data=shuffle(data)
    for i in range(4):
        data[:,i]=(data[:,i]-np.min(data[:,i]))/(np.max(data[:,i])-np.min(data[:,i]))
    train=np.array(data[:-20])
    test=np.array(data[-20:])
    return train,test
def init(inputnum,hiddennum,outnum,cIndex,Data):
    c=[]
    for i in cIndex:
        c.append(Data[i])
    c=np.array(c)
    b=[]
    for k in range(hiddennum):
        t=[]
        for i in range(len(c)):
            for j in range(len(c)):
                t.append(np.linalg.norm(c[i]-c[j],2))
        b.append([sum(t)/hiddennum])
    b=np.array(b)
    return c,b
def f(x,c,b):
    x=c-x
    X=[]
    for i in range(len(x)):
        X.append(-sum(x[i]*x[i])/(b[i]*b[i]))
    X=np.mat(X)
    return np.exp(X)
def Train():
    train,test=loadData("iris.csv")
    knnData=train[:,:-1]
    Center = KNN(knnData,120,10,0.001)
    print(Center)
    c,b=init(4,10,3,Center,train[:,:-1])
    ho=[]
    T=[]
    for i in train:
        x=i[:-1]
        ho.append(f(x,c,b))
        lab=np.zeros(3)
        lab[i[-1]]+=1
        T.append(lab)
    T=np.array(T)
    ho=np.array(ho)
    ho=ho.reshape(130,10)
    hopiv=np.linalg.pinv(ho)
    w=np.dot(hopiv,T)
    w=w.T
    #测试
    ans=[]
    for i in test:
        x=i[:-1]
        hout=f(x,c,b)
        out=np.dot(w,hout)
        if np.argmax(out)==i[-1]:
            ans.append(1)
        else:
            ans.append(0)
    print(sum(ans)/len(ans))
    return sum(ans)/len(ans)
def main():
    acc=[]
    for i in range(10):
        acc.append(Train())
    plt.bar(range(len(acc)),acc)
    plt.show()
    pass
main()

三、有监督学习（梯度下降法）
前两种办法的无需训练，得到的模型基本就是数学解析解了，其性能（至少是在鸢尾花数据集上）应该是要比梯度下降法确定参数要优秀一些。
用梯度下降法训练RBFNN，就是纯粹的反向传播算法了，先随机初始化待确定参数c，b，w之后通过模型对样本的误差通过梯度下降的办法来指导权值的更新。
误差对c，b，w的梯度的表达式为：



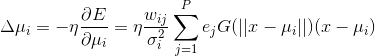
将上式用矩阵形式表出，更新权值的代码为：

    c=np.add(c,-lr*np.dot(np.dot(np.dot((w.T/(b*b)),err),hout.T),(c-x)))
    x_=x-c
    x_=np.mat([np.sum(i)*np.sum(i) for i in x_]).T
    b=np.add(b,-lr*np.dot(np.dot(np.dot(hout,err.T),(w.T/(b*b*b)).T),x_))
    w-=lr*np.dot(err,hout.T)

应用梯度下降法，训练RBFNN的步骤为：
1.参数初始化

def init(inputnum,hiddennum,outnum):
    c=np.random.normal(0.0, 1, (hiddennum, inputnum))
    b=np.random.normal(0.0, 1, (hiddennum, 1))
    w=np.random.normal(0.0, 1, (outnum,hiddennum))
    return c,b,w

2.前向计算，得到预测值

    hout=f(x,c,b)
    out=np.dot(w,hout)

3.计算误差，并更新参数

    err=out-y
    c=np.add(c,-lr*np.dot(np.dot(np.dot((w.T/(b*b)),err),hout.T),(c-x)))
    x_=x-c
    x_=np.mat([np.sum(i)*np.sum(i) for i in x_]).T
    b=np.add(b,-lr*np.dot(np.dot(np.dot(hout,err.T),(w.T/(b*b*b)).T),x_))
    w-=lr*np.dot(err,hout.T)
    return float(sum(abs(err)))

设置最大训练轮次为300轮，将每轮的平均损失和在测试集上的准确率可视化展示出来，如下图所示。最后的准确率基本稳定在95%左右。

上图所展示的模型的隐藏层节点数为25个（继续用10个隐藏层节点的话准确率远不如前两种方法）。而且梯度下降法确定一次模型参数的时间，就足够前两种方法确定100次模型了！（确实是较为耗时）

参考代码如下

import pandas as pd 
import numpy as np 
from sklearn.utils import shuffle
import matplotlib.pyplot as plt
def loadData(filename):
    fp = open(filename)
    data = np.array(pd.read_csv(filename,header=None).values)
    lab=["Iris-setosa","Iris-versicolor","Iris-virginica"]
    for i in range(len(data)):
        for j in range(3):
            if data[i][-1]==lab[j]:
                data[i][-1]=j
    data=shuffle(data)
    for i in range(4):
        data[:,i]=(data[:,i]-np.min(data[:,i]))/(np.max(data[:,i])-np.min(data[:,i]))
    train=np.array(data[:-20])
    test=np.array(data[-20:])
    return train,test
def init(inputnum,hiddennum,outnum):
    c=np.random.normal(0.0, 1, (hiddennum, inputnum))
    b=np.random.normal(0.0, 1, (hiddennum, 1))
    w=np.random.normal(0.0, 1, (outnum,hiddennum))
    return c,b,w
def f(x,c,b):
    x=c-x
    X=[]
    for i in range(len(x)):
        X.append(-sum(x[i]*x[i])/(b[i]*b[i]))
    X=np.mat(X)
    return np.exp(X)
def trainW(c,b,w,x,y,lr):
    hout=f(x,c,b)
    out=np.dot(w,hout)
    err=out-y
    c=np.add(c,-lr*np.dot(np.dot(np.dot((w.T/(b*b)),err),hout.T),(c-x)))
    x_=x-c
    x_=np.mat([np.sum(i)*np.sum(i) for i in x_]).T
    b=np.add(b,-lr*np.dot(np.dot(np.dot(hout,err.T),(w.T/(b*b*b)).T),x_))
    w-=lr*np.dot(err,hout.T)
    return float(sum(abs(err)))
def Train():
    train,test=loadData("iris.csv")
    c,b,w=init(4,25,3)
    loss=[]
    acc=[]
    for e in range(300):
        loss_=[]
        for i in train:
            x=i[:-1]
            y=np.zeros((3,1))
            y[i[-1]]+=1
            loss_.append(trainW(c,b,w,x,y,0.01))
        loss.append(sum(loss_)/len(loss_))
        acc_=[]
        for i in test:
            x=i[:-1]
            y=np.zeros((3,1))
            y[i[-1]]+=1
            hout=f(x,c,b)
            out=np.dot(w,hout)
            if(np.argmax(out)==i[-1]):
                acc_.append(1)
            else:
                acc_.append(0)
        acc.append(sum(acc_)/len(acc_))
    plt.subplot(2,1,1)
    plt.plot(loss)
    plt.subplot(2,1,2)
    plt.plot(acc)
    print(acc)
    plt.show()
Train()

鸢尾花数据集
样本个数也比较少，就直接贴出来吧

5.1,3.5,1.4,0.2,Iris-setosa
4.9,3.0,1.4,0.2,Iris-setosa
4.7,3.2,1.3,0.2,Iris-setosa
4.6,3.1,1.5,0.2,Iris-setosa
5.0,3.6,1.4,0.2,Iris-setosa
5.4,3.9,1.7,0.4,Iris-setosa
4.6,3.4,1.4,0.3,Iris-setosa
5.0,3.4,1.5,0.2,Iris-setosa
4.4,2.9,1.4,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
5.4,3.7,1.5,0.2,Iris-setosa
4.8,3.4,1.6,0.2,Iris-setosa
4.8,3.0,1.4,0.1,Iris-setosa
4.3,3.0,1.1,0.1,Iris-setosa
5.8,4.0,1.2,0.2,Iris-setosa
5.7,4.4,1.5,0.4,Iris-setosa
5.4,3.9,1.3,0.4,Iris-setosa
5.1,3.5,1.4,0.3,Iris-setosa
5.7,3.8,1.7,0.3,Iris-setosa
5.1,3.8,1.5,0.3,Iris-setosa
5.4,3.4,1.7,0.2,Iris-setosa
5.1,3.7,1.5,0.4,Iris-setosa
4.6,3.6,1.0,0.2,Iris-setosa
5.1,3.3,1.7,0.5,Iris-setosa
4.8,3.4,1.9,0.2,Iris-setosa
5.0,3.0,1.6,0.2,Iris-setosa
5.0,3.4,1.6,0.4,Iris-setosa
5.2,3.5,1.5,0.2,Iris-setosa
5.2,3.4,1.4,0.2,Iris-setosa
4.7,3.2,1.6,0.2,Iris-setosa
4.8,3.1,1.6,0.2,Iris-setosa
5.4,3.4,1.5,0.4,Iris-setosa
5.2,4.1,1.5,0.1,Iris-setosa
5.5,4.2,1.4,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
5.0,3.2,1.2,0.2,Iris-setosa
5.5,3.5,1.3,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
4.4,3.0,1.3,0.2,Iris-setosa
5.1,3.4,1.5,0.2,Iris-setosa
5.0,3.5,1.3,0.3,Iris-setosa
4.5,2.3,1.3,0.3,Iris-setosa
4.4,3.2,1.3,0.2,Iris-setosa
5.0,3.5,1.6,0.6,Iris-setosa
5.1,3.8,1.9,0.4,Iris-setosa
4.8,3.0,1.4,0.3,Iris-setosa
5.1,3.8,1.6,0.2,Iris-setosa
4.6,3.2,1.4,0.2,Iris-setosa
5.3,3.7,1.5,0.2,Iris-setosa
5.0,3.3,1.4,0.2,Iris-setosa
7.0,3.2,4.7,1.4,Iris-versicolor
6.4,3.2,4.5,1.5,Iris-versicolor
6.9,3.1,4.9,1.5,Iris-versicolor
5.5,2.3,4.0,1.3,Iris-versicolor
6.5,2.8,4.6,1.5,Iris-versicolor
5.7,2.8,4.5,1.3,Iris-versicolor
6.3,3.3,4.7,1.6,Iris-versicolor
4.9,2.4,3.3,1.0,Iris-versicolor
6.6,2.9,4.6,1.3,Iris-versicolor
5.2,2.7,3.9,1.4,Iris-versicolor
5.0,2.0,3.5,1.0,Iris-versicolor
5.9,3.0,4.2,1.5,Iris-versicolor
6.0,2.2,4.0,1.0,Iris-versicolor
6.1,2.9,4.7,1.4,Iris-versicolor
5.6,2.9,3.6,1.3,Iris-versicolor
6.7,3.1,4.4,1.4,Iris-versicolor
5.6,3.0,4.5,1.5,Iris-versicolor
5.8,2.7,4.1,1.0,Iris-versicolor
6.2,2.2,4.5,1.5,Iris-versicolor
5.6,2.5,3.9,1.1,Iris-versicolor
5.9,3.2,4.8,1.8,Iris-versicolor
6.1,2.8,4.0,1.3,Iris-versicolor
6.3,2.5,4.9,1.5,Iris-versicolor
6.1,2.8,4.7,1.2,Iris-versicolor
6.4,2.9,4.3,1.3,Iris-versicolor
6.6,3.0,4.4,1.4,Iris-versicolor
6.8,2.8,4.8,1.4,Iris-versicolor
6.7,3.0,5.0,1.7,Iris-versicolor
6.0,2.9,4.5,1.5,Iris-versicolor
5.7,2.6,3.5,1.0,Iris-versicolor
5.5,2.4,3.8,1.1,Iris-versicolor
5.5,2.4,3.7,1.0,Iris-versicolor
5.8,2.7,3.9,1.2,Iris-versicolor
6.0,2.7,5.1,1.6,Iris-versicolor
5.4,3.0,4.5,1.5,Iris-versicolor
6.0,3.4,4.5,1.6,Iris-versicolor
6.7,3.1,4.7,1.5,Iris-versicolor
6.3,2.3,4.4,1.3,Iris-versicolor
5.6,3.0,4.1,1.3,Iris-versicolor
5.5,2.5,4.0,1.3,Iris-versicolor
5.5,2.6,4.4,1.2,Iris-versicolor
6.1,3.0,4.6,1.4,Iris-versicolor
5.8,2.6,4.0,1.2,Iris-versicolor
5.0,2.3,3.3,1.0,Iris-versicolor
5.6,2.7,4.2,1.3,Iris-versicolor
5.7,3.0,4.2,1.2,Iris-versicolor
5.7,2.9,4.2,1.3,Iris-versicolor
6.2,2.9,4.3,1.3,Iris-versicolor
5.1,2.5,3.0,1.1,Iris-versicolor
5.7,2.8,4.1,1.3,Iris-versicolor
6.3,3.3,6.0,2.5,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
7.1,3.0,5.9,2.1,Iris-virginica
6.3,2.9,5.6,1.8,Iris-virginica
6.5,3.0,5.8,2.2,Iris-virginica
7.6,3.0,6.6,2.1,Iris-virginica
4.9,2.5,4.5,1.7,Iris-virginica
7.3,2.9,6.3,1.8,Iris-virginica
6.7,2.5,5.8,1.8,Iris-virginica
7.2,3.6,6.1,2.5,Iris-virginica
6.5,3.2,5.1,2.0,Iris-virginica
6.4,2.7,5.3,1.9,Iris-virginica
6.8,3.0,5.5,2.1,Iris-virginica
5.7,2.5,5.0,2.0,Iris-virginica
5.8,2.8,5.1,2.4,Iris-virginica
6.4,3.2,5.3,2.3,Iris-virginica
6.5,3.0,5.5,1.8,Iris-virginica
7.7,3.8,6.7,2.2,Iris-virginica
7.7,2.6,6.9,2.3,Iris-virginica
6.0,2.2,5.0,1.5,Iris-virginica
6.9,3.2,5.7,2.3,Iris-virginica
5.6,2.8,4.9,2.0,Iris-virginica
7.7,2.8,6.7,2.0,Iris-virginica
6.3,2.7,4.9,1.8,Iris-virginica
6.7,3.3,5.7,2.1,Iris-virginica
7.2,3.2,6.0,1.8,Iris-virginica
6.2,2.8,4.8,1.8,Iris-virginica
6.1,3.0,4.9,1.8,Iris-virginica
6.4,2.8,5.6,2.1,Iris-virginica
7.2,3.0,5.8,1.6,Iris-virginica
7.4,2.8,6.1,1.9,Iris-virginica
7.9,3.8,6.4,2.0,Iris-virginica
6.4,2.8,5.6,2.2,Iris-virginica
6.3,2.8,5.1,1.5,Iris-virginica
6.1,2.6,5.6,1.4,Iris-virginica
7.7,3.0,6.1,2.3,Iris-virginica
6.3,3.4,5.6,2.4,Iris-virginica
6.4,3.1,5.5,1.8,Iris-virginica
6.0,3.0,4.8,1.8,Iris-virginica
6.9,3.1,5.4,2.1,Iris-virginica
6.7,3.1,5.6,2.4,Iris-virginica
6.9,3.1,5.1,2.3,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
6.8,3.2,5.9,2.3,Iris-virginica
6.7,3.3,5.7,2.5,Iris-virginica
6.7,3.0,5.2,2.3,Iris-virginica
6.3,2.5,5.0,1.9,Iris-virginica
6.5,3.0,5.2,2.0,Iris-virginica
6.2,3.4,5.4,2.3,Iris-virginica
5.9,3.0,5.1,1.8,Iris-virginica

一家之言，如有问题欢迎大家指出。