深度学习 - 从卷积神经网络开始理解认识深度学习

对于会者来说，卷积的理论知识，数学公式是入门，但对于真正的新手小白来说，掌握卷积的理论和推导就已经可以算是学有所成了（是我没错了），这篇文章不说入门知识，而是说一说如何入门。

目录

计算机生成图像原理：

RGB三原色（red，green，blue）

计算机显示一个像素点

计算机显示多个像素点

卷积神经网络

什么是卷积

卷积在干什么

卷积网络又是什么

卷积网络又在干什么

---

计算机生成图像原理：

RGB三原色（red，green，blue）

 

        RGB是最常用的彩色模式，RGB分别代表红、绿、蓝三原色，RGB采用此模式每个像素占用3个字节（一个字节8位），分别用于表示颜色的R、G、B分量（255、255、255）属加色模式0-255（黑色-白色)。
        它的特点就是文件小、色彩丰富且饱满。RGB模式是一种发光的彩色模式 屏幕上显示的图像，就一般都是以RGB模式，因为显示器的物理结构就是遵循RGB的。

计算机显示一个像素点

RGB也是计算机生成颜色的原理，我们拿一个蓝色的像素点来说：

R：[ 0 ] G：[ 0 ] B：[ 255 ]

这三个矩阵叠加就是一个蓝色的像素点。

再来看看这些：

• R：[ 0 ] G：[ 0 ] B：[ 155 ]

        一个浅一点的蓝色像素点

• R：[ 0 ] G：[ 0 ] B：[ 55 ]     

        一个更浅一点的蓝色像素点

• R：[ 255 ] G：[ 0 ] B：[ 255 ]       

        一个粉色的像素点

计算机显示多个像素点

上面的矩阵是一个像素点，那么多个像素点呢？看看下面这个矩阵

[
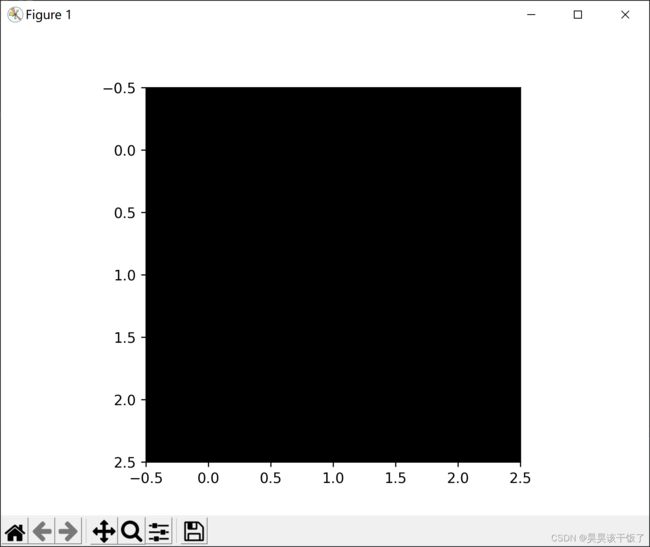
    [[0],[0],[0]],
    [[0],[0],[0]],
    [[0],[0],[0]],
]

猜猜他出来的是什么？

再来猜猜这个：

[
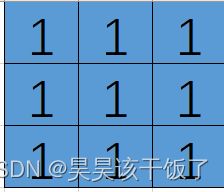
    [[1],[1],[1]],
    [[1],[0],[1]],
    [[1],[1],[1]],
]

每个像素相连，出来了一副 图 ，只有这么几个像素点的图，而那些说几千万像素的相机，什么意思呢？一张图有几千万像素点。

我们一起画一个十字，要求是，中心的位置颜色更深，怎么做呢？

[
    [[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[0.5],[0.5],[0.5],[0.5],[0],[0.5],[0.5],[0.5],[0.5],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1]],
]

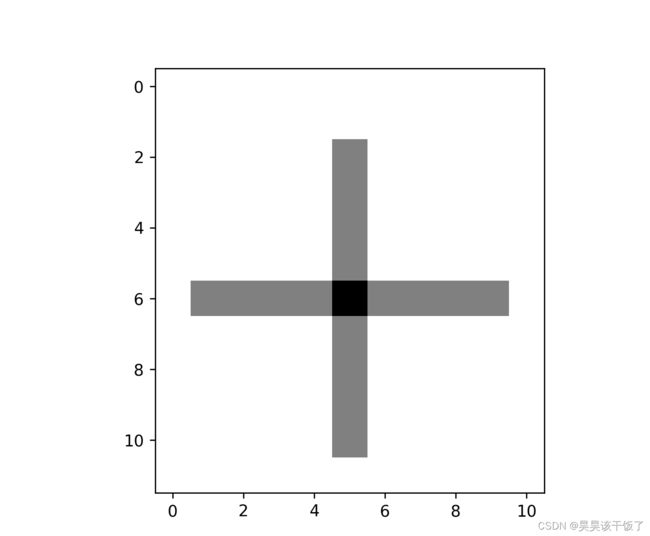
看看样子：

        中心是0，其他位置是1，浅灰色是0.5，加上其他的颜色，所以说，矩阵是计算机图像的根本，让计算机学习图像，实际上就是学习这些矩阵的规律 。

最后，一定有人好奇，图像和矩阵是怎么联系起来的呢，代码给你，简单的调用库函数：

import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np

bb = np.array([
    [[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[0.5],[0.5],[0.5],[0.5],[0],[0.5],[0.5],[0.5],[0.5],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[0.5],[1],[1],[1],[1],[1]],
    [[1],[1],[1],[1],[1],[1],[1],[1],[1],[1],[1]],
])
plt.figure()    #创建画布
plt.imshow(bb, cmap='gray') #将bb矩阵放上去
plt.show()  #展示画布

卷积神经网络

        好了，现在让我们用一个熟悉的矩阵来看看卷积在做什么吧，这一次的卷积之旅大概分为下面几步：

什么是卷积

卷和积两个字，目前你可以认为是 滑动 -> 叠加

深入一些来说：

1. 进行“卷”（滑动）的目的其实是施加一种约束，它指定了在“积”的时候以什么为参照。它指定了在哪个特定位置的前后进行“积”，指定了在哪个位置的周边进行累积处理。

2.从“积”的过程可以看到，我们得到的叠加值，是个全局的概念。卷积的结果是不仅跟当前时刻输入的值有关，也跟过去所有时刻输入的值都有关系，考虑了对过去的所有输入的效果的累积。

        在图像处理的中，卷积处理的结果，其实就是把每个像素周边的，甚至是整个图像的像素都考虑进来，对当前像素进行某种加权处理。所以说，“积”是全局概念，或者说是一种“混合”。

那么具体怎么滑动，怎么叠加呢？

卷积在干什么

看一个我们熟悉的矩阵：

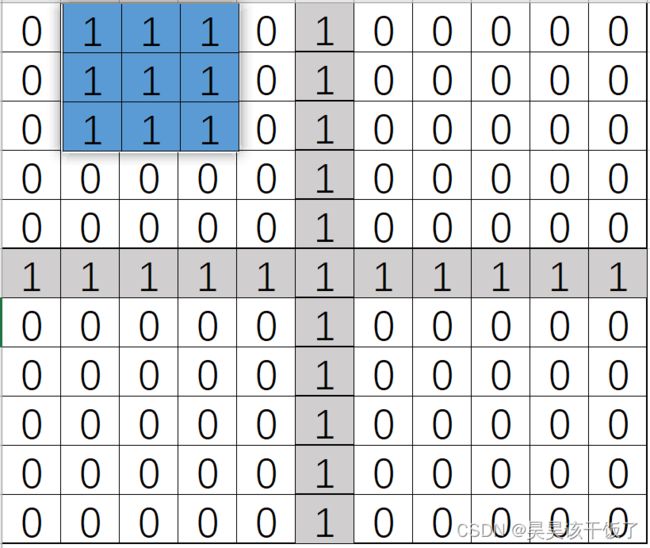
 卷积在做的事情就是用一个卷积核（其实另一个小的矩阵，我们姑且让这个矩阵的每一个值都是1吧）不断地滑动，滑到这个十字架图形矩阵的每一个位置，将它们的值，积 起来。

我们用这个卷积核来卷：

卷积核和覆盖的对阵位置数字相乘，再全部加和起来，最后每一次都出来一个数字。

第一次：

得到了一个0,第二次：

还是0 。

 是的，在后面他会出来3：

当卷积核覆盖的位置是这种时，都是3。

        似乎逻辑简单到人也可以计算了，似乎这并不需要借助计算机，但是，这只是一个简单的黑白图，只是一个十字图形，也只有一百多个像素，而真正的图片，三色构成彩色，复杂的交织图案，百万起步的像素。。。

卷积网络又是什么

        所以，一次卷积明显不够，而将一次卷积后生成的所有数字，组成新的矩阵，继续卷积操作，由多个卷积层和其他辅助的神经网络层不断重复组成的，就是网络

卷积网络又在干什么

说白了，卷积网络就是处理矩阵的多个步骤重复叠加，卷积神经网络归根结底就是一类工具，它并不是一种独特的科学技术。

1、可以将音频之类的文件转化为图像，甚至一些其他领域的东西也可以用图像的方式表达出来，从而传递一种可视化的信息；

2、可以很好地去处理各种东西，比如进行文本处理、视频处理等等。

百闻不如一见，如果真的感兴趣，欢迎私信我。也欢迎留言讨论指正，翘首以待~