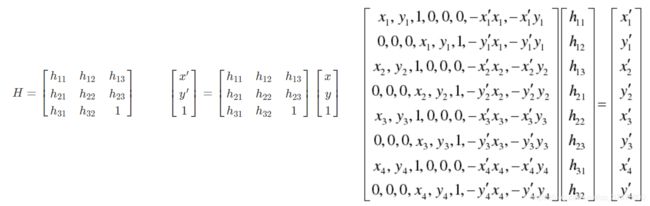OpenCV-图像特征harris角点检测/SIFT函数/特征匹配-05

图像特征-harris角点检测

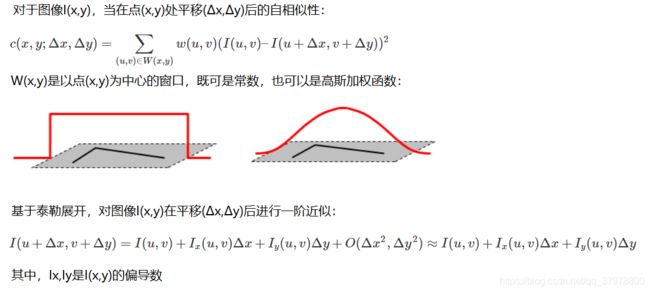
基本原理

R>0 角点
R≈0 平坦区域
R<0 边界

总结一下Harris算法流程

获取点数据后,计算Ix 和 Iy
整合矩阵,求特征值
比较特征值大小
非极大值抑制NMS,过滤掉不是那么角的

OpenCV中怎么检测Harris

cv2.cornerHarris()
img： 数据类型为 float32 的入图像
blockSize： 角点检测中指定区域的大小，前面提到的w(u,v),可能是个高斯函数
ksize： 就像Sobel求导中使用的窗口大小
k： 取值参数为 [0,04,0.06]. 默认0.04
返回dst：输出图像

import cv2 
import numpy as np

img = cv2.imread('chessboard.jpg') #读取图片
print ('img.shape:',img.shape)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)# 转换成灰度图
# gray = np.float32(gray)
dst = cv2.cornerHarris(gray, 2, 3, 0.04) # 执行检测
print ('dst.shape:',dst.shape)

# dst.max是最大值,一定是角点
# 只要dst中满足0.01倍的最大值，就判定为角点，要求较高的也可以设置为其他倍数
img[dst>0.01*dst.max()]=[0,0,255]
cv2.imshow('dst',img) 
cv2.waitKey(0) 
cv2.destroyAllWindows()
cv2.imwrite('test_1_dst.jpg',img)

Scale Invariant Feature Transform（SIFT）

图像尺度空间

在一定的范围内，无论物体是大还是小，人眼都可以分辨出来，然而计算机要有相同的能力却很难，所以要让机器能够对物体在不同尺度下有一个统一的认知，就需要考虑图像在不同的尺度下都存在的特点。

尺度空间的获取通常使用高斯模糊来实现


不同σ的高斯函数决定了对图像的平滑程度，越大的σ值对应的图像越模糊。

高斯差分金字塔（DOG）

DoG空间极值检测

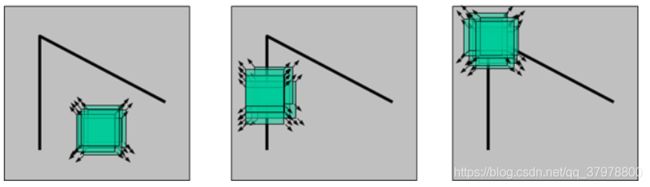
为了寻找尺度空间的极值点，每个像素点要和其图像域（同一尺度空间）和尺度域（相邻的尺度空间）的所有相邻点进行比较，当其大于（或者小于）所有相邻点时，该点就是极值点。如下图所示，中间的检测点要和其所在图像的3×3邻域8个像素点，以及其相邻的上下两层的3×3领域18个像素点，共26个像素点进行比较。

关键点的精确定位

这些候选关键点是DOG空间的局部极值点，而且这些极值点均为离散的点，精确定位极值点的一种方法是，对尺度空间DoG函数进行曲线拟合，计算其极值点，从而实现关键点的精确定位。


消除边界响应

特征点的主方向

每个特征点可以得到三个信息(x,y,σ,θ)，即位置、尺度和方向。具有多个方向的关键点可以被复制成多份，然后将方向值分别赋给复制后的特征点，一个特征点就产生了多个坐标、尺度相等，但是方向不同的特征点。

生成特征描述

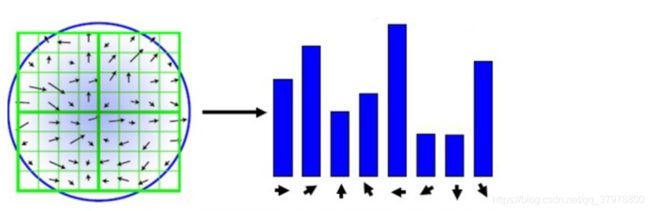
在完成关键点的梯度计算后，使用直方图统计邻域内像素的梯度和方向。

为了保证特征矢量的旋转不变性，要以特征点为中心，在附近邻域内将坐标轴旋转θ角度，即将坐标轴旋转为特征点的主方向。

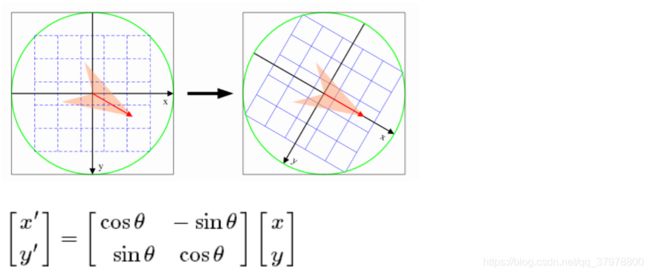
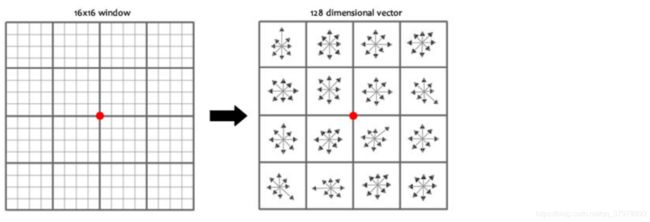
旋转之后的主方向为中心取8x8的窗口，求每个像素的梯度幅值和方向，箭头方向代表梯度方向，长度代表梯度幅值，然后利用高斯窗口对其进行加权运算，最后在每个4x4的小块上绘制8个方向的梯度直方图，计算每个梯度方向的累加值，即可形成一个种子点，即每个特征的由4个种子点组成，每个种子点有8个方向的向量信息。

论文中建议对每个关键点使用4x4共16个种子点来描述，这样一个关键点就会产生128维的SIFT特征向量。

使用open cv前最好先安装anaconda.由于部分函数涉及专利问题，如sift和surf，所以需要使用opencv-python 3.4.1.15版本的

但是蛋疼的是python需要3.6的才能支持该版本，所以在此之前先要安装python3.6的环境，也可以直接安装低版本的anaconda,安装环境方法如下：

conda create --name py3.6 python=3.6 #创建python3.6环境
conda activate py3.6 #进入该环境
pip install opencv-python==3.4.1.15 #安装opencv
pip install opencv-contrib-python==3.4.1.15 #安装opencv的其他包

opencv SIFT函数

import cv2
import numpy as np

img = cv2.imread('test_1.jpg')# 读取图像
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 灰度图

sift = cv2.xfeatures2d.SIFT_create() # 实例化一个sift
kp = sift.detect(gray, None) # 传进去一个图像

img = cv2.drawKeypoints(gray, kp, img) # 绘制关键点

cv2.imshow('drawKeypoints', img)
cv2.waitKey(0)
cv2.destroyAllWindows()

计算特征

kp, des = sift.compute(gray, kp)

print (np.array(kp).shape)

des.shape

特征匹配

### Brute-Force蛮力匹配

import cv2 
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

img1 = cv2.imread('box.png', 0)
img2 = cv2.imread('box_in_scene.png', 0)

def cv_show(name,img):
    cv2.imshow(name, img)
    cv2.waitKey(0)
    cv2.destroyAllWindows()

cv_show('img1',img1)

cv_show('img2',img2)

sift = cv2.xfeatures2d.SIFT_create()

kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)

# crossCheck表示两个特征点要互相匹，例如A中的第i个特征点与B中的第j个特征点最近的，并且B中的第j个特征点到A中的第i个特征点也是 
#NORM_L2: 归一化数组的(欧几里德距离)，如果其他特征计算方法需要考虑不同的匹配计算方式
bf = cv2.BFMatcher(crossCheck=True)

1对1的匹配

matches = bf.match(des1, des2)
matches = sorted(matches, key=lambda x: x.distance)

img3 = cv2.drawMatches(img1, kp1, img2, kp2, matches[:10], None,flags=2)

cv_show('img3',img3)

k对最佳匹配

bf = cv2.BFMatcher()
matches = bf.knnMatch(des1, des2, k=2)

good = []
for m, n in matches:
    if m.distance < 0.75 * n.distance:
        good.append([m])

img3 = cv2.drawMatchesKnn(img1,kp1,img2,kp2,good,None,flags=2)

cv_show('img3',img3)

如果需要更快速完成操作，可以尝试使用cv2.FlannBasedMatcher

随机抽样一致算法（Random sample consensus，RANSAC）

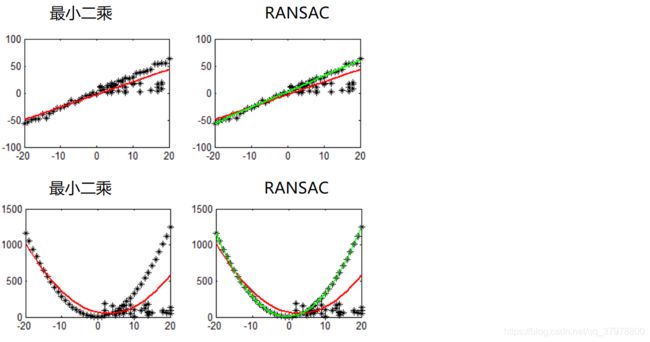
选择初始样本点进行拟合，给定一个容忍范围，不断进行迭代

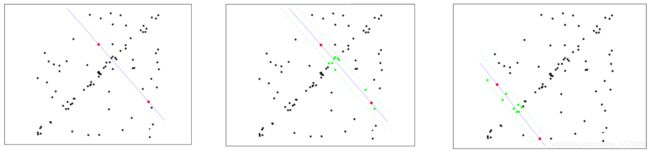
每一次拟合后，容差范围内都有对应的数据点数，找出数据点个数最多的情况，就是最终的拟合结果

单应性矩阵