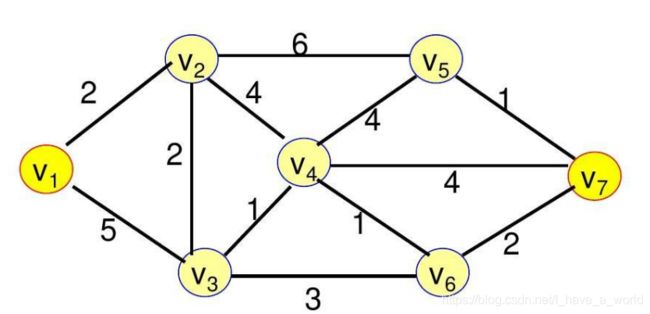
3.注意：不能处理带负权的图
4.模板：
暴力模板
时间，空间复杂度均为O(n^2)，使用邻接表空间复杂度可降到O(m)
void dijkstra(int s) {
for (int i = 0; i <= n; i++) dis[i] = inf, vis[i] = 0; //注意dis[x=0]=inf
dis[s] = 0;
for (int i = 1; i < n; i++) {
int x = 0;
for (int j = 1; j <= n; j++)
if (!vis[j] && (x == 0 || dis[j] < dis[x])) x = j;
vis[x] = 1;
for (int j = 1; j <= n; j++)
if (dis[x] + g[x][j] < dis[j]) //如果不能到达，g[i][j]=inf
dis[j] = dis[x] + g[x][j];
}
}
堆优化模板
时间复杂度大概在O(mlogm)，还是很可观的（和sfpa混着来）。
P4779 【模板】单源最短路径（标准版）：注意是有向图
注意在什么时候标记vis[i]=1。应该在遍历一个i之后标记，写在遍历前也不影响——总之要理解。
#include
#define read(x) scanf("%d", &x)
#define print(a, c) printf("%d%c", a, c)
#define pb push_back
using namespace std;
const int maxn = 2e5 + 10;
const int inf = 2e9;
struct node {
int to, w;
node() {}
node(int _to, int _w) { to = _to, w = _w; }
};
struct pii {
int fi, se;
pii() {}
pii(int _fi, int _se) { fi = _fi, se = _se; }
bool operator<(pii b) const { return fi > b.fi; }
};
priority_queue q;
int n, m, s;
int u, v, w;
vector g[maxn];
int dis[maxn], vis[maxn];
void dijkstra(int s) {
for (int i = 1; i <= n; i++) dis[i] = inf, vis[i] = 0;
dis[s] = 0;
q.push(pii(0, s));
while (!q.empty()) {
pii now = q.top();
q.pop();
int d = now.fi, i = now.se; //距离和下标
if (vis[i])
continue; //之前标记过的点仍然在优先队列中取不出来很正常，到时候取出来
vis[i] = 1;
for (auto j : g[i]) {
if (vis[j.to]) continue;
//松弛操作
if (d + j.w < dis[j.to]) {
dis[j.to] = d + j.w;
q.push(pii(dis[j.to], j.to));
}
}
}
}
signed main() {
read(n), read(m), read(s);
for (int i = 1; i <= m; i++) {
read(u), read(v), read(w);
g[u].pb(node(v, w));
}
dijkstra(s);
for (int i = 1; i <= n; i++) print(dis[i], ' ');
return 0;
}
其他优化
1.参考oi-wiki
2.1 暴力：O(n^2+m)=O(n^2)
2.2 堆：O(mlogn)
2.3 priority_queue:O(mlogm)
2.4 zkw线短树：O(mlogn+n)=O(mlogn)
PS:了解了一下线段树，主要在于维护整个区间内最小的值以及它的下标。与常数小的堆优化（与上面的priority_queue）时间复杂度差不多。
2.5 Fibonacci堆：O(nlogn+m)
ps：还没去了解，感觉没多大必要
2)SPFA
1.介绍：对bellman_ford算法的一个队列优化。可用于求单源最短路。（可以处理求含负权的最短路，但是不能处理含负环的最短路）
2.操作：类似于bfs，每次检查可以更新同时没在队列中的点放进去继续等待更新，等一个都不能更新就自动出来了。操作也简单，码德，简直绝了。
3.时间复杂度：稀疏图中O(km)，k为常数。稠密图中退化到O(nm)
4.模板：
标准模板
P4779 【模板】单源最短路径（标准版）（和上面是一个题）：以下代码并不能过这题，很nice，不愧是专门卡spfa的题。不过，spfa代码还是正确的。
#include
#define read(x) scanf("%d", &x)
#define print(a, c) printf("%d%c", a, c)
#define pb push_back
using namespace std;
const int maxn = 2e5 + 10;
const int inf = 2e9;
struct node {
int to, w;
node() {}
node(int _to, int _w) { to = _to, w = _w; }
};
int n, m, s;
int u, v, w;
vector g[maxn];
int dis[maxn], vis[maxn];
void spfa() {
for (int i = 1; i <= n; i++) dis[i] = inf, vis[i] = 0;
dis[s] = 0;
queue q;
q.push(s), vis[s] = 1;
while (!q.empty()) {
int x = q.front();
q.pop(), vis[x] = 0; //毕竟一般也不会有自环
for (auto i : g[x]) {
/* if
* (vis[i.to])continue;不能这样，这个算法在队列中不代表不能够优化！——应该放在下面！*/
if (dis[x] + i.w < dis[i.to]) {
dis[i.to] = dis[x] + i.w;
if (!vis[i.to]) q.push(i.to), vis[i.to] = 1;
}
}
}
}
signed main() {
read(n), read(m), read(s);
for (int i = 1; i <= m; i++) {
read(u), read(v), read(w);
g[u].pb(node(v, w));
}
spfa();
for (int i = 1; i <= n; i++) print(dis[i], ' ');
return 0;
}
2.多源最短路
1)Floyd
1.介绍：（可以处理求含负权的最短路，但是不能处理含负环的最短路）
2.挺多拓展的：传递闭包，最长/短路，最小/“大”瓶颈路，判正负环。最小环？？
模板:
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
3.传递闭包
介绍：mp[i][j]=1表示存在i到j的路径。floyd求出所有的mp[i][j]。
模板:
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) mp[i][j] |= mp[i][k] & mp[k][j];
Median Weight Bead POJ - 1975
题意：有n(1~99，且为奇数)个珠子，m对数a,b表示珠子的质量a>b。问重量不可能为中位数的数的珠子的个数。
题解: 传递闭包，最后某个珠子有n/2+1及以上颗珠子质量大于或有n/2+1及以上颗珠子质量小于它，那么这颗珠子的质量一定不可能为中位数。
代码：
#include
#include
#include
#include
#include
#define read(x) scanf("%d", &x)
#define print(a, c) printf("%d%c", a, c)
#define mst(a, x) memset(a, x, sizeof(a))
using namespace std;
const int maxn = 99 + 10;
int n, m, g[maxn][maxn], mp[maxn][maxn];
int in[maxn], out[maxn], u, v;
signed main() {
int T;
read(T);
while (T--) {
read(n), read(m);
mst(in, 0), mst(out, 0), mst(g, 0), mst(mp, 0);
for (int i = 1; i <= m; i++) {
read(u), read(v);
g[u][v] = 1; //这个一般用作记权值
mp[u][v] = 1; //初始化。这个一般记u能不能到达v
}
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) mp[i][j] |= mp[i][k] & mp[k][j];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (mp[i][j]) out[i]++, in[j]++;
// for (int i = 1; i <= n; i++) cout << in[i] << " " << out[i] << endl;
int ans = 0;
for (int i = 1; i <= n; i++)
ans += (in[i] >= n / 2 + 1 || out[i] >= n / 2 + 1);
print(ans, '\n');
}
return 0;
}
4.最短路径树
1.概念：最短路构成的一棵树（也知识一个概念罢了，很简单，但是拓展性也并不是很强）。
2.应用
1)最短路径树计数
黑暗城堡 LibreOJ - 10064
题意：n(1<=n<=1000)个点，m条无向边，每条边长度为li（1<=l<=200）,求不同最短路径树（最开始从1出发）的数量（结果对2^31-1取余）。
题解：求出每个点的前一个节点的数量（满足对短路，即dis[u]+w==dis[v]，dis[i]表示节点s到i的最短距离），最后相乘取余。
操作：在松弛操作的时候操作（spfa的话建议用第二种操作，第一种或多或少有些问题！）或者在求出所有点的最短路之后操作。
模板：
ps：也是这题的AC代码
/*操作1：在松弛操作的地方做修改*/
#include
#define int long long
#define read(x) scanf("%lld", &x)
#define print(a, c) printf("%lld%c", a, c)
// #define ll long long
#define pb push_back
using namespace std;
const int maxn = 1e3 + 10;
const int maxm = 1e6 + 10;
const int inf = 2147483647; // 1<<31-1
struct node {
int to, w;
node() {}
node(int _to, int _w) { to = _to, w = _w; }
};
struct pii {
int fi, se;
pii() {}
pii(int _fi, int _se) { fi = _fi, se = _se; }
bool operator<(pii b) const { return fi > b.fi; }
};
priority_queue q;
int n, m;
int u, v, w;
vector g[maxn];
int dis[maxn], vis[maxn], pre[maxn];
void dijkstra() {
for (int i = 1; i <= n; i++) dis[i] = inf, vis[i] = 0, pre[i] = 0;
dis[1] = 0, pre[1] = 1;
q.push(pii(0, 1));
while (!q.empty()) {
pii now = q.top();
q.pop();
int d = now.fi, i = now.se; //距离和下标
if (vis[i])
continue; //之前标记过的点仍然在优先队列中取不出来很正常，到时候取出来
vis[i] = 1;
for (auto j : g[i]) {
if (vis[j.to]) continue;
//松弛操作
if (d + j.w == dis[j.to]) pre[j.to]++; //操作1第一步
if (d + j.w < dis[j.to]) {
dis[j.to] = d + j.w;
q.push(pii(dis[j.to], j.to)), pre[j.to] = 1; //操作一第二步
}
}
}
}
signed main() {
read(n), read(m);
for (int i = 1; i <= m; i++) {
read(u), read(v), read(w);
g[u].pb(node(v, w)), g[v].pb(node(u, w));
}
dijkstra();
int ans = 1;
// for (int i = 1; i <= n; i++) cout << i << ":::" << pre[i] << endl;
for (int i = 1; i <= n; i++) ans = (ans * pre[i]) % inf;
print(ans, '\n');
return 0;
}
/*操作2：即在求出dis之后再计数*/
dijkstra();
for (int i = 1; i <= n; i++) pre[i] = 0;
pre[1] = 1;
for (int i = 1; i <= n; i++) {
for (auto j : g[i]) {
if (dis[i] + j.w == dis[j.to]) pre[j.to]++;
}
}
2)去掉图中一条边之后最短路径树大小（dis之和）是否有变化
题意：n个城市（n<=100），m条无向边，每两个城市之间都走最小路。从小到大打印所有公路序号，这些公路满足：去掉之后至少有两个城市之间的路程变大了。
题解：暴力每个起点，分别建最短路径树，然后枚举这树上的每条边，不经过这条边建一颗最短路径树，求出该起点到其他每个点的最短路径和，如果大于没去掉这条边之前的值，一定满足条件。说明，枚举任意起点的时候可以建任意一颗最短路径树，因为如果存在多颗最短路径树，同时枚举的某条边如果可以替代，那么他们是可以相互替代的，去掉任何一颗都不会改变最短路径和！！！
代码：就附上了，知道思路即可，做法仍是最短路+建最短路径树。
ps:暂时就以上两个应用吧，毕竟自己每遇到过。
5.最短路计数
1.概念：字面意思
2.操作：与最短路径树的操作几乎一样，只需要做一些改动：pre初始化为0；pre[s]=1；然后每次遇到dis[u]==dis[v]的时候pre[v]+=pre[u]；松弛操作的时候pre[v]=pre[u]就ok了。
对比最短路径树：pre初始化为0；pre[s]=1；然后每次遇到dis[u]==dis[v]的时候pre[v]++；松弛操作的时候pre[v]=1就ok了。
3.例题：P1608 路径统计
题意：n个点，最开始在1，要到达n。问最短路径是多少，有多少条。如果一条都没有，就打印no。n<=2000,m<=n*(n-1),保证无自环，不保证无重边，另外所有路是单向的！——重边取最小值，而不是如果想等的有x条就表示这里有x种走法。
模板：
void dijkstra() {
for (int i = 1; i <= n; i++) dis[i] = inf, vis[i] = 0, pre[i] = 0;
dis[1] = 0, pre[1] = 1;
q.push(pii(0, 1)); //小顶堆
while (!q.empty()) {
pii now = q.top();
q.pop();
int d = now.fi, i = now.se; //距离和下标
if (vis[i])
continue; //之前标记过的点仍然在优先队列中取不出来很正常，到时候取出来
vis[i] = 1;
for (auto j : g[i]) {
if (vis[j.to]) continue;
//松弛操作
if (d + j.w == dis[j.to]) pre[j.to] += pre[i]; //操作一第一步
if (d + j.w < dis[j.to]) {
dis[j.to] = d + j.w;
q.push(pii(dis[j.to], j.to)),
pre[j.to] = pre[i]; //操作一第二步
}
}
}
// dis[i]==inf，或者说pre[n]=0时表示无路径
(dis[n] == inf) ? puts("No answer")
: (print(dis[n], ' '), print(pre[n], '\n'));
}
6.分层图最短路
参考博客
图论之分层图最短路总结 与经典例题
专题·最短路【including Dijkstra， SPFA，Floyd，传递闭包，二维最短路，分层图最短路，最短路计数……
介绍
只是在建图的时候不一样，除此之外就是跑个普通最短路。当然，难的也就是建图。
用分层图的几种情况
1）k个不同集合的边。将每个集合建一层图，然后第k+1层建一个虚图（用于连接每一层，价值根据题意）。如小雨坐地铁。
2）有k个机会免费走一条路。建k+1个相同的图，每层之间用有边的点连接起来，代价为0。没走一层表示用了一次机会。如P4568 [JLOI2011]飞行路线。
3）有k个机会逆向行驶。建k+1个相同的图，每层之间用有边的两点之间的逆向边连接，权值不变，没走一层表示用了一次机会（这里应该必须是有向图罢，不然没啥意义）。
例题
小雨坐地铁
题目描述：n（1~1000）个车站，m（1~500）条地铁线。每次经过第 i 条地铁线需要花费ai（1~100），在这条地铁线上，每经过一个车站多花费bi（1~100），每条线上有ci（1~n）个车站（按顺序依次输入沿途站，注意是双向的）。
题解：情况1）。注意进入第m+1层的时候花费0，从m+1层进入的时候才花费ax（相当于从n*m+s到n*m+t）。多读题，图别建错；注意建图之后点的总数。
代码：
#include
#define int long long
#define read(x) scanf("%lld", &x)
#define print(a, c) printf("%lld%c", a, c)
#define pb push_back
#define mst(a, x) memset(a, x, sizeof(a))
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
const int maxn = 500 * 1000 + 1000 + 10;
const int mod = 1e9 + 7;
const int inf = 1e9;
struct node {
int to, w;
node() {}
node(int _to, int _w) { to = _to, w = _w; }
};
struct pii {
int fi, se; // dis,id
pii() {}
pii(int _fi, int _se) { fi = _fi, se = _se; }
bool operator<(pii b) const {
return fi > b.fi;
} //平常的就大顶堆，否则小顶堆。这里小顶堆
};
int n, m, s, t;
int a, b, c;
vector g[maxn];
int dis[maxn], vis[maxn];
priority_queue q;
void dijkstra(int s) {
for (int i = 1; i <= n * m + n; i++) dis[i] = inf;
dis[s] = 0, vis[s] = 1;
q.push(pii(0, s));
while (!q.empty()) {
pii now = q.top();
q.pop();
int x = now.se, w = now.fi;
for (auto i : g[x]) {
if (i.w + dis[x] < dis[i.to]) {
dis[i.to] = i.w + dis[x], vis[i.to] = 1;
q.push(pii(dis[i.to], i.to));
}
}
}
}
signed main() {
read(n), read(m), read(s), read(t);
for (int i = 1; i <= m; i++) {
read(a), read(b), read(c);
int now, pre;
//建第k张图
for (int j = 1; j <= c; j++) {
read(now);
if (j > 1) {
int u = (i - 1) * n + pre, v = (i - 1) * n + now, w = b;
g[u].pb(node(v, w));
g[v].pb(node(u, w));
}
//连虚图（相当于中转站）
int u = (i - 1) * n + now, v = n * m + now, w = a;
g[u].pb(node(v, 0)); //进入需要0
g[v].pb(node(u, w)); //出来代表从一条线进入新的一条线(每次都要花钱)
pre = now;
}
}
dijkstra(n * m + s); //从n*m+t出来
// for (int i = 1; i <= 10; i++) print(dis[i], ' ');
// cout << endl;
if (dis[n * m + t] == inf)
puts("-1");
else
print(dis[n * m + t], '\n');
return 0;
}
P4568 [JLOI2011]飞行路线
题意：n（2~1e4）个点，m（1~5e4）条无向带权边（权值大小在0~1e3），可以最多坐k（0~10）次免费航班。问从s到t的最小花费。
题解：情况2）。难点在建图上，见代码：：：
代码：
#include
#define int long long
#define read(x) scanf("%lld", &x)
#define print(a, c) printf("%lld%c", a, c)
#define pb push_back
#define mst(a, x) memset(a, x, sizeof(a))
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
const int maxn = 1e4 * 12 + +10;
const int mod = 1e9 + 7;
const int inf = 1e9;
struct node {
int to, w;
node() {}
node(int _to, int _w) { to = _to, w = _w; }
};
struct pii {
int fi, se; // dis,id
pii() {}
pii(int _fi, int _se) { fi = _fi, se = _se; }
bool operator<(pii b) const {
return fi > b.fi;
} //正常为大顶堆，不正常为小顶堆
};
int n, m, k, s, t;
int u, v, w;
vector g[maxn];
int dis[maxn], vis[maxn];
priority_queue q;
void dijkstra(int s) {
for (int i = 0; i <= n * k + n; i++) dis[i] = inf;
dis[s] = 0, vis[s] = 1;
q.push(pii(0, s));
while (!q.empty()) {
pii now = q.top();
q.pop();
int x = now.se, w = now.fi;
for (auto i : g[x]) {
if (i.w + dis[x] < dis[i.to]) {
dis[i.to] = i.w + dis[x], vis[i.to] = 1;
q.push(pii(dis[i.to], i.to));
}
}
}
}
signed main() {
read(n), read(m), read(k);
read(s), read(t);
for (int i = 1; i <= m; i++) {
read(u), read(v), read(w);
// 0层图
g[u].pb(node(v, w)), g[v].pb(node(u, w));
for (int j = 1; j <= k; j++) {
// 1~k层图
g[j * n + u].pb(node(j * n + v, w));
g[j * n + v].pb(node(j * n + u, w));
//上一层与这一层连接
g[(j - 1) * n + u].pb(node(j * n + v, 0));
g[(j - 1) * n + v].pb(node(j * n + u, 0));
}
}
//传到n*k+t，最后直接取dis[n*k+t];
for (int i = 1; i <= k; i++) g[(i - 1) * n + t].pb(node(i * n + t, 0));
dijkstra(s); //从n*m+t出来
// for (int i = 0; i <= 10; i++) print(dis[i], ' ');
// cout << endl;
print(dis[n * k + t], '\n');
return 0;
}
/*
5 6 1
0 4
0 1 5
1 2 5
2 3 5
3 4 5
2 3 3
0 2 100
*/
情况3）：与情况2）的差别只在建图，有这个意识就好。
ps：也不止与这些应用。
7.k短路
Remmarguts' Date POJ - 2449
题意：N(1~1000)个点，M(0~1e5)条有向带权边，问点s到t的第k(1~1000)短路的长度。
题解：k短路模板题。首先建一个反向路,dis[i]表示到t的最短路，然后bfs，得到一次t记一次数。bfs具体操作见代码。
注意：1.s可能到不了t
2.s到t可能没有k条路（s-t的任意路径上有环的话，s到t的路就可以视作有无数条）
3.s==t的时候k要加1，因为bfs的时候最开始的s被算作t（长度为0）。
4.知道操作，但是还不是完全理解（所以必然记不牢靠，总结下模板，记不住至少还可以用）。
模板1
#include
#include
#include
#include
#include
#include
#include
// #define int long long
#define read(x) scanf("%d", &x)
#define print(a, c) printf("%d%c", a, c)
#define pb push_back
#define mst(a, x) memset(a, x, sizeof(a))
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
const int maxn = 1e3 + 10;
const int mod = 1e9 + 7;
const int inf = 1e9;
struct node {
int to, w;
node() {}
node(int _to, int _w) { to = _to, w = _w; }
};
struct pii {
int i, dis, dis1;
pii() {}
pii(int _i, int _dis, int _dis1) { i = _i, dis = _dis, dis1 = _dis1; }
bool operator<(pii b) const { return dis + dis1 > b.dis + b.dis1; }
};
int n, m, s, t, k;
int u, v, w;
vector g[maxn], re[maxn];
int dis[maxn], vis[maxn];
void spfa(int s) {
for (int i = 0; i <= n; i++) dis[i] = inf;
dis[s] = 0;
queue q;
q.push(s), vis[s] = 1;
while (!q.empty()) {
int x = q.front();
q.pop();
vis[x] = 0;
// sbpoj，c++11都不支持
for (int j = 0; j < re[x].size(); j++) {
node i = re[x][j];
if (i.w + dis[x] < dis[i.to]) {
dis[i.to] = i.w + dis[x];
if (vis[i.to] == 0) q.push(i.to), vis[i.to] = 1;
}
}
}
}
priority_queue q;
void bfs(int s) {
q.push(pii(s, 0, 0));
int cnt = 0;
while (!q.empty()) {
pii now = q.top();
q.pop();
if (now.i == t) {
cnt++;
if (cnt == k) {
print(now.dis, '\n');
return;
}
}
for (int j = 0; j < g[now.i].size(); j++) {
node i = g[now.i][j];
q.push(pii(i.to, now.dis + i.w, dis[i.to]));
}
}
puts("-1"); //这是什么情况？——毕竟单向路径，可能s->t都没有k条路
}
signed main() {
read(n), read(m);
for (int i = 1; i <= m; i++) {
read(u), read(v), read(w);
g[u].pb(node(v, w));
re[v].pb(node(u, w));
}
read(s), read(t), read(k);
spfa(t);
if (dis[s] == inf)
puts("-1");
else {
if (s == t) k++; //为啥。看bfs哪里。s也被视作t了，这个t不算
bfs(s);
}
return 0;
}
/*
input:::
2 2
1 2 5
2 1 4
1 2 2
output:::
14
*/
P2901 [USACO08MAR]Cow Jogging G
题意: 给定n(1~1000)个点，m(1~1e4)条带权有向边（无重边），还有一个数k(1~100)。要求n到1的前k小的路径大小，如果第i小的路径不存在就输出-1。
题解：和上一题唯一不一样的就是这里要求输出前k小的数，上一题只需要输出第k小的数。
模板2
#include
// #define int long long
#define read(x) scanf("%d", &x)
#define print(a, c) printf("%d%c", a, c)
#define pb push_back
#define mst(a, x) memset(a, x, sizeof(a))
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
const int maxn = 1e3 + 10;
const int mod = 1e9 + 7;
const int inf = 1e9;
struct node {
int to, w;
node() {}
node(int _to, int _w) { to = _to, w = _w; }
};
struct pii {
int i, dis, dis1;
pii() {}
pii(int _i, int _dis, int _dis1) { i = _i, dis = _dis, dis1 = _dis1; }
bool operator<(pii b) const { return dis + dis1 > b.dis + b.dis1; }
};
int n, m, k;
int u, v, w;
vector g[maxn], re[maxn];
vector ans;
int dis[maxn], vis[maxn];
void spfa(int s) {
for (int i = 0; i <= n; i++) dis[i] = inf;
dis[s] = 0;
queue q;
q.push(s), vis[s] = 1;
while (!q.empty()) {
int x = q.front();
q.pop();
vis[x] = 0;
for (int j = 0; j < re[x].size(); j++) {
node i = re[x][j];
if (i.w + dis[x] < dis[i.to]) {
dis[i.to] = i.w + dis[x];
if (vis[i.to] == 0) q.push(i.to), vis[i.to] = 1;
}
}
}
}
priority_queue q;
void bfs(int s) {
q.push(pii(s, 0, 0));
int cnt = 0;
while (!q.empty()) {
pii now = q.top();
q.pop();
if (now.i == 1) {
cnt++;
ans.pb(now.dis);
if (cnt == k) return;
}
for (int j = 0; j < g[now.i].size(); j++) {
node i = g[now.i][j];
q.push(pii(i.to, now.dis + i.w, dis[i.to]));
}
}
while (ans.size() < k) ans.pb(-1);
}
signed main() {
read(n), read(m), read(k);
for (int i = 1; i <= m; i++) {
read(u), read(v), read(w);
g[u].pb(node(v, w));
re[v].pb(node(u, w));
}
spfa(1);
if (dis[n] == inf)
for (int i = 1; i <= k; i++) ans.pb(-1);
else {
if (n == 1) k++; //为啥。看bfs哪里。s也被视作t了，这个t不算
bfs(n);
}
for (auto i : ans) print(i, '\n');
return 0;
}
/*
input:::
5 8 7
5 4 1
5 3 1
5 2 1
5 1 1
4 3 4
3 1 1
3 2 1
2 1 1
output:::
1
2
2
3
6
7
-1
*/
九、求两队点的最短路的最大重合路径长度
写在最后
现在可能还欠缺的知识：最小环，求两队点的最短路的最大重合路径长度。另一个博客独有的？判正环，负环，“最大瓶颈路”/最小瓶颈路，差分约束等等。还挺多没涉及到的emmm。恕我直言，凭我的废物属性，大概要三五个月下一轮学习的时候才会把两个博客整合（+补充欠缺的知识emmm）。现在拉拉进度罢先。
(三)最小生成树
1.oi-wiki最小生成树（知识还挺多）
1）边刷题边看。
2）Kruskal 算法——加边：将所有边排序，然后利用并查集每次连接两块没有连接的块，连接线条数满n-1的时候即生成了最小生成树。
3）才发现这是裸的kruskal：不过，yy能力也很重要（要不是看了题解，就算能记起最小生成树也不一定会用啊）。
2.繁凡さん
1.基础算法：
1）克鲁斯卡尔：加n-1条边
时间复杂度:O(elogn)
并查集查询与合并：
int find(int x) { return (x == fa[x]) ? x : fa[x] = find(fa[x]); }
void merge(int x, int y) {
int fx = find(x), fy = find(y);
if (dep[fx] < dep[fy])
fa[fx] = fy;
else {
fa[fy] = fx;
if (dep[fx] == dep[fy]) dep[fy]++;
}
}
POJ-1251-Jungle Roads代码：
#include
#include
#include
#include
#include
#include
#include
#include
#define int long long
#define dbg(x) cout << #x << "===" << x << endl;
using namespace std;
const int maxn = 100 + 10;
struct node {
int u, v, dis;
node() {}
node(int _u, int _v, int _dis) { u = _u, v = _v, dis = _dis; }
bool operator<(node b) const { return dis < b.dis; }
} s[maxn];
int n, m, dis;
char c0, c1;
int u, v;
int fa[maxn], dep[maxn];
int find(int x) { return (x == fa[x]) ? x : fa[x] = find(fa[x]); }
void merge(int x, int y) {
int fx = find(x), fy = find(y);
if (dep[fx] < dep[fy])
fa[fx] = fy;
else {
fa[fy] = fx;
if (dep[fx] == dep[fy]) dep[fy]++;
}
}
signed main() {
while (cin >> n) {
if (n == 0) break;
memset(dep, 0, sizeof(dep)), memset(fa, 0, sizeof(fa));
int cnt = 0;
for (int i = 1; i <= n - 1; i++) {
cin >> c0 >> m;
// cout << c0 << " " << m << endl;
u = c0 - 'A' + 1;
if (u < 1 || u > 26) break;
for (int j = 1; j <= m; j++) {
cin >> c1 >> dis;
// cout << c1 << ' ' << dis << endl;
v = c1 - 'A' + 1;
s[++cnt] = node(u, v, dis);
}
}
sort(s + 1, s + 1 + cnt);
//dbg(cnt);
//for(int i=1;i<=cnt;i++) cout<
2）prim：加n-1个点（不算第一个点）
时间复杂度：O(n^2)
空间复杂度：O(n^2)
模板：
int vis[maxn], d[maxn];
int prim() {
for (int i = 1; i <= n; i++) vis[i] = 0, d[i] = 9e18; //初始化
int ans = 0;
for (int i = 1; i <= n; i++) {
int t = -1;
for (int j = 1; j <= n; j++) {
if (vis[j] == 0 && (t == -1 || d[j] < d[t])) t = j;
}
vis[t] = 1; //标记
if (i > 1) ans += d[t]; //第一个点不加，i==1是d[t]=1e9
for (int j = 1; j <= n; j++)
d[j] = min(d[j], mp[t][j]); //二维数组注意空间复杂度
}
return ans;
}
3）Boruvka算法（结合prim与克鲁斯卡尔）
1）时间复杂度是严格的O(elogn)。每次最少可以另连通块数量少一半，最多调用logn次Boruvka，每次复杂度为O(elogn)（logn为并查集）。
2）与prim的差别：这里是多连通块拓展增广图，prim是单连通块拓展。
3）据(oi-wiki评论)说这个算法可拓展性很强。
4）目前还没遇到一题可以用克鲁斯卡尔/prim但是恰恰不能用Boruvka。（之后再来复习）
5）题目：P3366 【模板】最小生成树
模板：
bool Boruvka() {
// best[u]=id记录u-v，id为u-v的下标。其中u,v不在同一连通块，且u-v是所有满足条件的最小权值边。
int best[maxn];
memset(best, 0, sizeof(best));
//枚举所有边，更新best。（与Prim差不多，不同的是这里是多个连通块拓展增广路，prim是一个连通块）
for (int i = 1; i <= m; i++) {
int fx = find(s[i].u), fy = find(s[i].v);
if (fx == fy) continue;
if (s[i].w < s[best[fx]].w || best[fx] == 0) best[fx] = i;
if (s[i].w < s[best[fy]].w || best[fy] == 0) best[fy] = i;
}
//枚举所有s[best[i]]边，判断是否能够连线（与克鲁斯卡尔完全一样的操作）
bool f = false;
for (int i = 1; i <= n && cx + 1 < n; i++) {
int fx = find(s[best[i]].u), fy = find(s[best[i]].v);
if (fx == fy) continue;
merge(fx, fy);
ans += s[best[i]].w;
cx++;
f = true; //表示还可能继续更新，如果!f一定不能继续更新
}
return f;
}
2.最小生成森林
题目：P1195 口袋的天空
题意：给定n(1~1e3)多云，m(1~1e4)条线（下标为u,v的云相连的代价为dis），求将这n朵云通过这些线连接成k朵的最小花费。
题解:克鲁斯卡尔，遍历所有边如果连线条数为n-k则说明有答案，否则不能连成k条边。
代码：
#include
// #define int long long
#define read(x) scanf("%d", &x)
#define print(a, c) printf("%d%c", a, c)
#define dbg(x) cout << #x << ">>>" << x << endl;
using namespace std;
const int maxn = 1e4 + 10;
struct node {
int u, v, dis;
node() {}
node(int _u, int _v, int _dis) { u = _u, v = _v, dis = _dis; }
void out(int i) {
cout << ">>>" << i << ":::" << u << " " << v << " " << dis << endl;
}
bool operator<(node b) { return dis < b.dis; }
} s[maxn];
int n, m, k;
int fa[maxn], dep[maxn];
int find(int x) { return (x == fa[x]) ? x : fa[x] = find(fa[x]); }
void merge(int x, int y) {
int fx = find(x), fy = find(y);
if (dep[fx] < dep[fy])
fa[fx] = fy;
else {
fa[fy] = fx;
if (dep[fx] == dep[fy]) dep[fy]++;
}
}
signed main() {
read(n), read(m), read(k);
for (int i = 1; i <= m; i++) {
read(s[i].u), read(s[i].v), read(s[i].dis);
}
sort(s + 1, s + 1 + m);
for (int i = 1; i <= n; i++) fa[i] = i;
int ans = 0, cx = 0;
for (int i = 1; i <= m && cx + k < n; i++) {
int fu = find(s[i].u), fv = find(s[i].v);
if (fu != fv) merge(fu, fv), ans += s[i].dis, cx++;
}
if (k > n || cx + k != n)
puts("No Answer");
else
print(ans, '\n');
return 0;
}
ps:提前返回main函数，应该也是要return 0的，不然可能有某种错误（尽管我平时也没发现会有什么后果）。
3.判断最小生成树的唯一性
求非严格次小生成树看是否和最小生成树相等，如果不相等那么就唯一。但其实可以更简单（简单的多）。
1.上博文中可以用一句话解释：如果在选一个点加进来的时候，有两条及以上的路径可以选择，那么这个最小生成树就就是不唯一的。
图：
2.代码：操作的时候要注意，抓住一个点，加入这个点的时候才判断。
3.操作也简单，理解也容易，唯一不好的就是复杂度得像prim一样O(n^2)
4.瓶颈生成树
1.定义：最大权值最小的生成树。
2.性质：最小生成树一定是瓶颈生成树，瓶颈生成树不一定是最小生成树。
2.题目：POJ-2395-Out of Hay
代码就略了，把最小生成树算法中的求和改成求n-1条边的最大值即可。
5.次小生成树（严格&非严格）
参考：oi-wiki、繁凡さん
次小生成树:所有生成树权值和第二小的生成树。
严格次小生成树：权值和大于最小生成树的生成树
非严格次小生成树:权值和大于等于最小生成树的生成树（最小生成树不唯一等价于次小生成树为非严格次小生成树）
求解方法一：先求最小生成树T，然后枚举所有在T上的边，求min(T-w+w')，w为T上u-v路径上的最大值，w'为途中u-v其他所有路径上的最小的最大边（非严格：w'>=w，严格：w'>w）。
时间复杂度：O(mlogm+nm)。nm为求所有u-v路径的最小的最大值的复杂度。一般不是用这种方式，因为不容易优化。
求解方法二：先求最小生成树T，然后枚举所有不在T上的边，求min(T-w+w')。w'为枚举的这条边，w为T上u-v路径上的最大值。
时间复杂度:O(mlogm+nn)。nn为求T上所有u-v路径的最大值的复杂度（每个点作为祖先dfs一边即可），可以LCA倍增优化，优化后时间复杂度：O(mlogm)。
注意：用方法二求严格最小生成树，需要预处理T上u-v路径上的最大值以及严格次大值（不能等于最大值），如果枚举的这条边大于最大值，就替换最大值，等于的话就替换严格次大值。
代码实现：
题目：P4180 [BJWC2010]严格次小生成树
题意：n个点，m条线(n,m<=3e5)。求严格次小生成树大小。（输入不保证无自环）
题解：见上面方法一。
代码如下：（还敲了我好一会，有一些坑（我饭的错）需要注意，参考的博客：forezxl）
#include
#define int long long
#define dbg(x) cout << #x << ">>>>" << x << endl;
#define read(x) scanf("%lld", &x)
#define print(a, c) printf("%lld%c", a, c)
#define pb push_back
using namespace std;
const int maxn = 3e5 + 10;
const int mod = 1e9 + 7;
struct node {
int x, y, z;
node() {}
node(int _x, int _y, int _z) { x = _x, y = _y, z = _z; }
bool operator<(node b) const { return z < b.z; }
} s[maxn];
struct pii {
int to, w;
pii() {}
pii(int _to, int _w) { to = _to, w = _w; }
};
int n, m, x, y, z;
int fa[maxn], dep[maxn], cnt, vis[maxn];
int ans, cx, ret;
vector g[maxn];
int mx1[maxn][25], mx2[maxn][25], f[maxn][25]; // 1<<20
//并查集路径压缩+按秩优化
int find(int x) { return (x == fa[x]) ? x : fa[x] = find(fa[x]); }
void merge(int x, int y) {
int fx = find(x), fy = find(y);
if (dep[fx] < dep[fy])
fa[fx] = fy;
else {
fa[fy] = fx;
if (dep[fx] == dep[fy]) dep[fy]++;
}
}
//建最小生成树，顺便标记最小生成树所用的边
void add(int i) {
int x = s[i].x, y = s[i].y, z = s[i].z;
merge(x, y), ans += z, cx++; // kruskal
g[x].pb(pii(y, z)), g[y].pb(pii(x, z)); //建树
vis[i] = 1; //标记树上的点
}
//为求lca做准备，预处理dep以及mx1（mx1[i][0]表示该点向上2^0步的路径上的最大值）
void dfs(int x, int fa) {
for (auto i : g[x]) {
if (i.to == fa) continue;
dep[i.to] = dep[x] + 1;
f[i.to][0] = x, mx1[i.to][0] = i.w;
dfs(i.to, x);
}
}
// lca预处理，注意mx1,mx2的处理
void lca_init() {
for (int j = 1; j <= 20; j++)
for (int i = 1; i <= n; i++) {
f[i][j] = f[f[i][j - 1]][j - 1];
//分成两段！！！mx1[i][j],mx2[i][j]此前都为更新，即为0
mx1[i][j] = max(mx1[i][j - 1], mx1[f[i][j - 1]][j - 1]);
if (mx1[i][j - 1] == mx1[f[i][j - 1]][j - 1]) { //两段相等
mx2[i][j] = max(mx2[i][j - 1], mx2[f[i][j - 1]][j - 1]);
} else {
//注意这里是小于，因为不能等于mx1[i][j]。总之要理解
mx2[i][j] = min(mx1[i][j - 1], mx1[f[i][j - 1]][j - 1]);
mx2[i][j] = max(mx2[i][j], mx2[i][j - 1]);
mx2[i][j] = max(mx2[i][j], mx2[f[i][j - 1]][j - 1]);
}
}
}
//点x向上2^i步，更新res——res为更新（指换一条边使x-y仍然连接）的代价。
void calc(int &res, int x, int i, int z) {
if (z == mx1[x][i])
res = min(res, z - mx2[x][i]);
else
res = min(res, z - mx1[x][i]);
}
// lca的基操。
int query(int x, int y, int z) {
int res = 9e18;
if (dep[x] < dep[y]) swap(x, y);
//使dep[x]=dep[y];
for (int i = 20; i >= 0; i--) {
if (dep[f[x][i]] >= dep[y]) {
calc(res, x, i, z);
x = f[x][i];
}
}
if (x == y) return res;
for (int i = 20; i >= 0; i--) {
if (f[x][i] != f[y][i]) {
calc(res, x, i, z), calc(res, y, i, z);
x = f[x][i], y = f[y][i];
}
}
calc(res, x, 0, z), calc(res, y, 0, z);
return res;
}
signed main() {
/*输入，以及建最小生成树，大小为ans*/
read(n), read(m);
for (int i = 1; i <= m; i++) {
read(x), read(y), read(z);
if (x == y) continue; //自环
s[++cnt] = node(x, y, z);
}
sort(s + 1, s + 1 + cnt); //别忘了
for (int i = 1; i <= n; i++) fa[i] = i;
for (int i = 1; i <= cnt && cx + 1 < n; i++) {
int fu = find(s[i].x), fv = find(s[i].y);
if (fu != fv) add(i);
}
//需要预处理dep以及mx1,mx2
memset(dep, 0, sizeof(dep)), dep[1] = 1, dfs(1, 0);
lca_init();
//更新ret
ret = 9e18;
for (int i = 1; i <= cnt; i++) {
if (vis[i] == 0) {
ret = min(ret, query(s[i].x, s[i].y, s[i].z));
}
}
ans += ret;
print(ans, '\n');
return 0;
}
/*
5 6
1 2 1
1 3 2
2 4 3
3 5 4
3 4 3
4 5 6
*/
6.最小瓶颈路
最小瓶颈路定义：见题意。
最小瓶颈路性质:无向图构建的最小生成树上的任意两点间的路径一定为无向图中这两点的最小瓶颈路。
题目：BZOJ-3732-Network
题意：给定n个点（n<=1.5e4）,m条边（m<=3e4）。q次询问，每次询问这个无向图上任意两个点的最小瓶颈路，即这两点之间的所有路径中最大值的最小值（最小生成树）。
题解：裸题
解决方法一：爆改一下上面次小生成树的代码。
解决方法二：kruskal重构树——貌似可以解决很多问题，这里先提一下。一下代码就用这个实现以下罢（试试建kruskal重构树）
代码：
#include
#define int long long
#define read(x) scanf("%lld", &x)
#define print(a, c) printf("%lld%c", a, c)
#define pb push_back
#define dbg(x) cout << #x << ">>>" << x << endl
using namespace std;
const int maxn = 3e4 + 10;
struct node {
int x, y, z;
node() {}
node(int _x, int _y, int _z) { x = _x, y = _y, z = _z; }
bool operator<(node b) const { return z < b.z; }
void out(int i) { cout << i << ":::" << x << " " << y << " " << z << endl; }
} s[maxn];
int n, m, q, x, y, z;
int fa[maxn], dep[maxn], cnt, cx;
int val[maxn], id; // kruskal重构树大小为2*n-1
vector g[maxn];
int f[maxn][25];
int find(int x) { return (x == fa[x]) ? x : fa[x] = find(fa[x]); }
void dfs(int x, int fa) {
for (auto i : g[x]) {
if (i == fa) continue;
dep[i] = dep[x] + 1, f[i][0] = x;
dfs(i, x);
}
}
int get_lca(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
for (int j = 20; j >= 0; j--)
if (dep[f[x][j]] >= dep[y]) x = f[x][j];
if (x == y) return x;
for (int j = 20; j >= 0; j--)
if (f[x][j] != f[y][j]) x = f[x][j], y = f[y][j];
x = f[x][0], y = f[y][0];
return x;
}
signed main() {
read(n), read(m), read(q);
for (int i = 1; i <= m; i++) {
read(x), read(y), read(z);
if (x == y) continue;
s[++cnt] = node(x, y, z);
}
sort(s + 1, s + 1 + cnt);
// for (int i = 1; i <= cnt; i++) s[i].out(i);
//注意初始化2*n-1个节点
for (int i = 1; i <= 2 * n - 1; i++) fa[i] = i;
for (int i = 1; i <= cnt && cx + 1 < n; i++) {
int fu = find(s[i].x), fv = find(s[i].y);
if (fu != fv) {
cx++;
id = n + cx; //新节点下标
val[id] = s[i].z; //不需要特别排序，就按照加入的顺序
fa[fu] = id, fa[fv] = id;
g[id].pb(fu), g[id].pb(fv);
}
}
//注意要以2*n-1为根节点
dep[2 * n - 1] = 1;
dfs(2 * n - 1, 0);
// lca_init:::尽量写在下面？？？？居然忘了调用
for (int j = 1; j <= 20; j++)
for (int i = 1; i <= 2 * n - 1; i++) f[i][j] = f[f[i][j - 1]][j - 1];
while (q--) {
read(x), read(y);
print(val[get_lca(x, y)], '\n');
}
return 0;
}
7.kruskal重构树
1.参考博客：Kruskal重构树 学习笔记
2.操作：每次在kruskal连边的时候，两个节点的连通块的根节点（路径压缩之后，任意时刻某个点的find()函数，即为该连通块的根节点）分别作为左右子树，新建一个节点，下标为n+cx，权值为连接两条边的权值（因为kruskal是从小到大加入边）。
3.性质：任意两点的最小瓶颈路中的最大边权即为他们在kruskal树中lca的点权。
4.能解决的问题：因为它的一些性质，在解决一些问题的时候有着天然的优势。
1）求最小瓶颈路
2）给一个无向图。每次询问给一个点v以及一个值p，问从v点出发，只能走<=p的线段，每次最多可以走多少个点。
ps_one：而且kruskal结构尤其特殊：深度越大，值越小（我们可以将所有的父亲节点都弄成>n的，这样解决这个问题的时候都可以弄个特定的数组直接查询——二分查询，因为顺序一定）
ps_two：不断理解一些算法思想！！！！！！
5.操作代码：看上面的最小瓶颈路实现。
****目前算是完结了罢。
目录
写在前面
３.然后才轮得到进阶的内容（待学）。
一、网络流基础概念
二、网络流中的常见问题
三、最大流
Ford-Fulkerson 增广路算法：该方法通过寻找增广路来更新最大流，有 EK,dinic,SAP,ISAP 主流算法。
Edmond-Karp 动能算法（EK 算法）
矩阵实现模板
链式前向星实现模板
Dinic 算法
模板
ISAP & HLPP(Push-Relabel 预流推进算法)
四、最小割
UVA1660 电视网络 Cable TV Network点转化为边，无代码
五、费用流
最小费用最大流
最大费用最大流——模板 - 费用流
（四）网络流
写在前面
１.感觉这部分知识特别多，繁凡さん 大佬写了很多这方面的博客。
２.先基础学习一下罢。0x6A.图论 - 网络流初步。网络流常见问题包括三种：最大流，最小割，费用流
３.然后才轮得到进阶的内容（待学）。
4.后面发现网络流就是全套模板，最多Dinic，偶尔卡（不知道正式赛会不会卡）那就ISAP。遇到的时候，难点就是如何建图（比较抽象）。
1.先行知识
1）网络流基础概念
ｐｓ：最开始还是看视频很快理解这些概念的。
网络流(理论详解)
0x6A.图论 - 网络流初步
oi-wiki
1）可行流 :
在容量网络G中满足以下条件的网络流f,称为可行流.
弧流量限制条件: 0 < = f ( u , v ) < = c ( u , v ) 0<=f(u,v)<=c(u,v) 0<=f(u,v)<=c(u,v);
平衡条件:即流入一个点的流量要等于流出这个点的流量,(源点和汇点除外).
2）最大流：
在所有的可行流中，流量最大的流。ps：可能不是唯一的。
3）最小割：
割其实就是删边的意思，当然最小割就是割掉 X 条边来让 S 跟 T 不互通。我们要求 X 条边加起来的流量综合最小。这就是最小割问题。
4）最小费用最大流：
每条边都有一个费用，代表单位流量流过这条边的开销。我们要在求出最大流的同时，要求花费的费用最小。
5）其他名词：
- 零流 ：若网络流上每条弧上的流量都为0,则该网络流称为零流.
- 伪流：如果一个网络流只满足弧流量限制条件,不满足平衡条件,则这种网络流为伪流,或称为容量可行流.(在预流推进优化算法中使用)
- 增广路：在原图 G 中若一条从源点到汇点的路径上所有边的 剩余容量都大于 0，这条路被称为增广路
- 残量网络：可以理解为，残量网络中包括了那些还剩了流量空间的边构成的图，也包括虚边（即反向边）。
- 网络流的流量：从源点出去或者进入汇点的总流量。
2）网络流中的常见问题
有以下三种：最大流，最小割，费用流 。
2.最大流
概述：
- 我们有一张图，要求从源点流向汇点的最大流量（可以有很多条路到达汇点），就是我们的最大流问题。
- 最大流算法可以解决很多实际的问题，比如二分图的最大匹配数就等于网络的最大流量。
Ford-Fulkerson 增广路算法：该方法通过寻找增广路来更新最大流，有 EK,dinic,SAP,ISAP 主流算法。
- 精华部分：利用反向边，使程序有了一个后悔和改正的机会。
（恕我直言，并不必过多纠结算法的正确性，先入门嘛！）。
1）Edmond-Karp 动能算法（EK 算法）
这个算法很简单，就是BFS找增广路，然后对其进行增广。
- 精髓：建反向边，给予后悔的机会。（理解这里很重要）
- 怎么实现后悔1：最开始建边的时候建立正向边，权值为w，反向边权值为0（注意如果矩阵就g[a][b]+=w,g[b][a]+=0，链式前向星的话就只需要每次add(a,b,w),add(b,a,0)即可——视作两点之间可以有很多条边）。
- 怎么后悔2：每次更新残余网络的时候增广路上的正方向+=minn，反方向-=minn。使某两点的正向边与反向边之和始终为两边的容量和，并且任意一边的值都是剩下的容量以及反向边通过的流量，所以也并不需要考虑最开始是否能够环形流动（正反边都有容量）。
- 如果使邻接矩阵的话，反向边就是从g[a][b]变为g[b][a]。如果是链式前向星，那就在加边的时候连续加入正向和反向边，然后在用的时候直接 i xor 1 就可以了（i为边的编号）。不过注意，cnt应该从0或2开始设置，否则就达不到这种效果，因为总是要 （某偶数,该偶数+1）才能互相异或1得到对方。
- 最后注意，链式前向星的时候，增广路的前一个节点的记录方式也与邻接矩阵有一点不一样：x的前一个点到x点这条边的序号记为id[x]=i。
- 感觉总结的挺好的，唯一不好的是没有图。可以再找博客参考，比如 oi-wiki。
- 题目：P2740 [USACO4.2]草地排水Drainage Ditches：EK增广路，最大流模板
- 题意：n(1~200)条水管m(1~200)个点，源点为1，汇点为m。（a,b,c）表示有a到b容量为c的水管。求最大流。说明，两点之间可能不止一条水管；可能会出现水环形流动的情形（好像没啥卵用）。
矩阵实现模板
#include
#define read(x) scanf("%d", &x)
#define print(a, c) printf("%d%c", a, c)
using namespace std;
const int M = 2e2 + 10;
const int INF = 2e9;
//这里还没被坑过emmm，但总感觉需要注意一下，万一最小值恰好可以比1e9大一点点
int n, m, a, b, c;
int g[M][M];
int s, t;
int vis[M], pre[M], mi[M];
bool bfs() {
memset(vis, 0, sizeof(vis));
// pre,mi不用初始话整个数组。而且注意，这里不应该只初始化1~n，因为m才是节点的总数
queue q;
q.push(s), vis[s] = 1, mi[s] = INF; // mi只需要初始这里，pre则啥都不必
while (!q.empty()) {
int x = q.front();
q.pop();
// 1~m才是节点！n只是边数
for (int i = 1; i <= m; i++) {
if (!vis[i] && g[x][i] > 0) {
pre[i] = x, mi[i] = min(mi[x], g[x][i]);
vis[i] = 1, q.push(i);
if (i == t) return true;
}
}
}
return false;
}
int EK() {
int maxflow = 0;
while (bfs()) {
int x = t;
while (x != s) {
g[pre[x]][x] -= mi[t];
g[x][pre[x]] += mi[t];
// g[a][b]+g[b][a]守恒。我们可以不考虑是否两个方向都有容量，只要满足守恒条件即可（很容易理解的：总之g[b][a]表示g[b][a]剩下的容量以及g[a][b]经过的流量之和，永远不会超过它们的和）
x = pre[x];
}
maxflow += mi[t];
}
return maxflow;
}
signed main() {
read(n), read(m);
s = 1, t = m;
for (int i = 1; i <= n; i++) {
read(a), read(b), read(c);
g[a][b] += c;
//残余网络中的g[b][a]表示使用的这个方向的流量，g[a][b]表示剩下的这个方向的流量
}
print(EK(), '\n');
return 0;
}
链式前向星实现模板
第一次学会使用链式前向星：建图之（链式）前向星。因为感觉这里没人使用vector（ｖｅｃｔｏｒ不是很方便改边的样子？）
#include
#define read(x) scanf("%d", &x)
#define print(a, c) printf("%d%c", a, c)
using namespace std;
const int N = 2e2 + 10;
const int M = 2e2 + 10;
const int INF = 1e9;
struct Edge {
int to, w, next;
Edge(int _to = 0, int _w = 0, int _next = 0)
: to(_to), w(_w), next(_next) {}
} edge[N << 1]; // n为边的数量
int head[M], cnt; // m才为点的数量
int n, m, a, b, c, s, t;
void add(int u, int v, int w) {
edge[cnt] = Edge(v, w, head[u]), head[u] = cnt++;
edge[cnt] = Edge(u, 0, head[v]), head[v] = cnt++; //反向边
}
int vis[M], id[M], mi[M];
bool bfs() {
memset(vis, 0, sizeof(vis));
queue q;
q.push(s), vis[s] = 1, mi[s] = INF;
while (!q.empty()) {
int x = q.front();
q.pop();
for (int i = head[x]; ~i; i = edge[i].next) {
if (edge[i].w > 0) {
int y = edge[i].to;
if (vis[y]) continue;
mi[y] = min(mi[x], edge[i].w);
id[y] = i;
q.push(y), vis[y] = 1;
if (y == t) return true;
}
}
}
return false;
}
int EK() {
int res = 0, x;
while (bfs()) {
x = t;
while (x != s) {
int i = id[x];
//增广路中x表示一个点，id[x]表示x_pre（增广路中x的前一个点）到x这条边的序号
edge[i].w -= mi[t];
edge[i ^ 1].w += mi[t];
//反正正向边和反向边之和不大于容量。（环形咋办？？？）
x = edge[i ^ 1].to;
}
res += mi[t];
}
return res;
}
signed main() {
read(n), read(m);
// init
s = 1, t = m;
memset(head, -1, sizeof(head));
for (int i = 1; i <= n; i++) {
read(a), read(b), read(c);
add(a, b, c); //, add(b, a, 0); //不是邻接矩阵的话是不用考虑重边的
}
print(EK(), '\n');
return 0;
}
/*
5 4
1 2 40
1 4 20
2 4 20
2 3 30
3 4 10
*/
2）Dinic 算法
最大流（Edmonds-Karp，Dinic，ISAP，Push-Relabel 预流推进算法）
EK不够快？再学个Dinic吧
个人ACM模板总结（模板基于此）
实现过程：
1）每次增广前，通过bfs分层。这源点层数为0，其他点的层数为离源点的最近距离（前提条件：路径容量全大于0）；
2）然后bfs找最短增广路（基于bfs处理的dep一层一层增广（也要满足容量条件），增广路长度都为dep[t]）。每次dfs最大流答案加上流过点s的最大流量（具体操作见代码——递归实现）！！
3）重复1，2操作直到不存在到汇点的增广路。
Dinic的两个优化：
多路增广：每次找到一条增广路的时候，如果残余流量没有用完怎么办呢？我们可以利用残余部分流量，再找出一条增广路。这样就可以在一次 DFS 中找出多条增广路，大大提高了算法的效率。
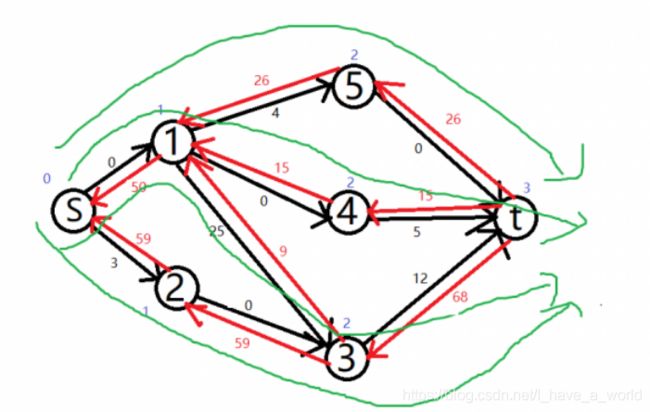
具体说明：蓝色表示点的深度dep。dfs的时候我们一下子找到四条增广路：s->1->4->t，s->1->2->t，s->2->3->t，s->1->3->t
当前弧优化：如果一条边已经被增广过，那么它就没有可能被增广第二次。那么，我们下一次进行增广的时候，就可以不必再走那些已经被增广过的边。
（具体证明看不懂，操作就简单了——bfs时预处理(now[v]=head[v])，dfs时now[v]=i 即可）
注意！踩过坑！当前弧优化建议放在bfs里面，虽然也可以放在Dinic中的循环里面（需要整体赋值），但是一是时间复杂度显然会变高一点，二是最开始的bfs之前也要整体赋值一下，否则bfs中i的开头要用head[i]才行。（网络流中首先注意到这个问题，做了kuangbin专题的第一题之后才全然搞明白这个是干什么的，优化在哪里——只优化在dfs中，不能优化在bfs中，用于替代head作为一个节点的链式前向星的结尾。一条边增广过，就没有可能再增广了（原来这里了解的也还是不够。总之知道怎么使用了！！）。bfs中只是可以初始化罢了，一定注意每次多路增广的时候都要初始化！）
复杂度：
1）具体时间复杂度
，事实上，往往达不到这个复杂度。据oi大佬博客EK不够快？再学个Dinic吧所说，学会Dinic就足够了。
2）在求解二分图最大匹配问题是，Ｄｉｎｉｃ算法的时间复杂度是
（学到二分图的时候再来看，应该是很简单的）。
ps：以下题目与上面EK的一样
- 题目：P2740 [USACO4.2]草地排水Drainage Ditches：EK增广路，最大流模板
- 题意：n(1~200)条水管m(1~200)个点，源点为1，汇点为m。（a,b,c）表示有a到b容量为c的水管。求最大流。说明，两点之间可能不止一条水管；可能会出现水环形流动的情形（好像没啥卵用）。
模板
#include
// #define int long long
#define read(x) scanf("%d", &x)
#define print(a, c) printf("%d%c", a, c)
#define pb push_back
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
const int M = 2e2 + 10;
const int INF = 1e9 + 10;
struct Edge {
int to, w, next;
Edge(int to = 0, int w = 0, int next = 0) : to(to), w(w), next(next) {}
} e[M << 1];
int n, m, a, b, c;
int s, t;
int head[M], cnt;
void add(int u, int v, int w) {
e[cnt] = Edge(v, w, head[u]), head[u] = cnt++;
e[cnt] = Edge(u, 0, head[v]), head[v] = cnt++;
}
int dep[M], now[M];
// bfs使dfs按照dep来增广，得到优化（具体证明就看不太懂了）。
bool bfs() {
memset(dep, -1, sizeof(dep));
queue q;
q.push(s), dep[s] = 0;
now[s] = head[s]; //当前弧优化（初始化）
while (!q.empty()) {
int x = q.front();
q.pop();
for (int i = now[x]; ~i; i = e[i].next) {
int v = e[i].to;
if (dep[v] == -1 && e[i].w > 0) {
dep[v] = dep[x] + 1;
now[v] = head[v]; //当前弧优化（初始化）。
q.push(v);
if (v == t) return true;
//遇到v==t即退出，因为=dep[v]的点
}
}
}
return false;
}
//一次dfs可能有几条增广路：见图
int dfs(int x, int flow) {
if (x == t) return flow;
int ans = 0;
// flow表示x点还能操作的流量，ans表示增广的这几路后流出x总最大流
// flow不剩下了，就没必要增广了
for (int i = now[x]; ~i && flow; i = e[i].next) {
int v = e[i].to;
now[x] = i;
//当前弧优化（这里才能得到优化，bfs中的只是初始化：另now[x]=head[x]）
if (dep[v] == dep[x] + 1 && e[i].w > 0) {
int tmp = dfs(v, min(flow, e[i].w));
// tmp为流过点v的最大流量
if (tmp == 0) dep[v] = -1; //剪枝，去掉增广完毕的点
e[i].w -= tmp;
e[i ^ 1].w += tmp;
ans += tmp;
flow -= tmp; //流过当前点（x）的流量累加（回溯）
}
}
return ans; //最后返回的是这几路增广的流量和
}
int Dinic() {
int maxflow = 0;
// bfs为真就一直dfs多路增广
while (bfs()) maxflow += dfs(s, INF);
return maxflow;
}
signed main() {
read(n), read(m);
memset(head, -1, sizeof(head));
s = 1, t = m;
for (int i = 1; i <= n; i++) {
read(a), read(b), read(c);
add(a, b, c);
}
print(Dinic(), '\n');
return 0;
}
3）ISAP
总结就是在Dinic上的优化（而且优化还挺多）。每次分层变为只分层一次（只bfs一次），其他分层在dfs中完成
参考博文
理解算法思想：oi-wiki、究级的最大流算法：ISAP与HLPP
代码实现：最大流（Edmonds-Karp，Dinic，ISAP，Push-Relabel 预流推进算法）、究级的最大流算法：ISAP与HLPP
复杂度：ISAP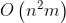 
一般达不到这个复杂度。该算法复杂度比Dinic略优越（一般来说会更快）
ps:增广路算法，玄学复杂度。
ISAP与dinic的两点不同：跑反图，不同的分层操作
1.跑反图
2.并不会每次都跑bfs
具体操作：
1.分层具体操作
（终止）
优化：当前弧优化和GAP优化
ps:增广路算法，玄学复杂度。
具体操作2：没想到这么简单，写起来比Dinic都还简单的既视感
1.bfs只需要一次，bfs只需要分层整个图（反向图），不需要考虑权值，也不用特意判断是否s，t连通（dep[s]=0即不连通）
2.dfs种前面部分与Dinic几乎完全一样（ISAP没有剪枝）
3.只是在遍历完x之后，才dep[x]++，使x与相连的深度为dep[x]-1的分割开（开始考虑深度为dep[x]的，同时dep[x]+=1）
4.注意初始化条件，dep[x]=0，是有实际意义的（到不了）
模板
// Luogu _P2740 [USACO4.2]草地排水Drainage Ditches
#include
// #define int long long
#define read(x) scanf("%d", &x)
#define print(a, c) printf("%d%c", a, c)
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
const int N = 2e2 + 10;
const int M = 4e2 + 10; //还是直接放在这里操作更舒服 M<<1多少容易弄错
const int INF = 1e9 + 7;
int n, m, s, t, a, b, c;
struct Edge {
int v, w, next;
Edge(int v = 0, int w = 0, int next = 0) : v(v), w(w), next(next) {}
} e[M];
int head[N], cnt, now[N];
void add(int u, int v, int w) {
e[cnt] = Edge(v, w, head[u]), head[u] = cnt++;
e[cnt] = Edge(u, 0, head[v]), head[v] = cnt++;
}
int dep[N], gap[N]; // gap优化：貌似优化力度挺大的
void bfs() {
for (int i = 0; i <= n; i++) dep[i] = gap[i] = 0, now[i] = head[i];
queue q;
q.push(t), dep[t] = 1, gap[dep[t]]++;
while (!q.empty()) {
int x = q.front();
q.pop();
for (int i = head[x]; ~i; i = e[i].next) {
int v = e[i].v;
if (!dep[v]) dep[v] = dep[x] + 1, q.push(v), gap[dep[v]]++;
}
}
}
int dfs(int x, int flow) {
if (x == t) return flow;
int ans = 0;
for (int i = now[x]; ~i; i = e[i].next) {
int v = e[i].v;
now[x] =
i; //怎么总是忘了弧优化的操作？甚至i=head[i]都来了？唉，还是太菜了
if (dep[x] == dep[v] + 1) {
int tmp = dfs(v, min(flow, e[i].w));
//对比Dinic，这里没有tmp==0则dep[v]=INF。如果有这里的剪枝，很明显就破坏了dep的值。就需要从新bfs更新dep了
e[i].w -= tmp;
e[i ^ 1].w += tmp;
ans += tmp;
flow -= tmp;
if (!flow) return ans;
// x没有跑完，不能够像Dinic一样直接跳出去返回ans，v点是跑完了，但是上一层dfs已经修改了dep[v]
// Dinic是~i&&flow。其实Dinic也可以像这里一样写
}
}
//上面的操作与Dinic几乎一模一样（与Dinic还是有一点差别的，没有剪枝！！）
//以下理解来源于https://www.luogu.com.cn/blog/ONE-PIECE/jiu-ji-di-zui-tai-liu-suan-fa-isap-yu-hlpp
//到这里的时候，x流出去的点已经全部流过了
//但是从前面流过的点还有剩余。更改dep使x与x流出的点分开
// emmm，虽然没有完全理解，但是知道怎么操作，虽然知道怎么操作，但是没有完全理解
//过一段时间再来看看
gap[dep[x]]--; //为什莫是这个地方dep[x]++？
if (gap[dep[x]] == 0) dep[s] = n + 1;
++gap[++dep[x]], now[x] = head[x]; //当前弧优化，在每次分层之后都要回到head
return ans;
}
int ISAP() {
int res = 0;
bfs();
// dbg(dep[s]);bfs有没有错误
while (dep[s] <= n && dep[s]) res += dfs(s, INF);
return res;
}
void init() {
memset(head, -1, sizeof(head)), cnt = 0;
read(m), read(n); // m为边数，n为点数
s = 1, t = n;
for (int i = 1; i <= m; i++) {
read(a), read(b), read(c);
add(a, b, c);
}
}
signed main() {
init();
int maxflow = ISAP();
print(maxflow, '\n');
return 0;
}
4）& HLPP(Push-Relabel 预流推进算法)
这两种算法目前了解一下即可。一般来说Dinic就已经足够了。究级的最大流算法：ISAP与HLPP（ISAP已补充）
复杂度：ISA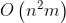P ，HLPP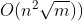 
Push-Relabel 预流推进算法（感觉暂时没必要）
ps：ｏｉ－ｗｉｋｉ这一部分没有看，感觉各路大佬也都没有学这个内容。
3.最小割
概述：将某s，t分为两部分需要切除的边的权值的最小值。
解法：最小割在数值上与最大流相等，但在本身性质上与网络流无任何关系。
所以将题目转化为最小割问题之后，Dinic一下即可。
模板：先略了，与Dinic一样。
UVA1660 电视网络 Cable TV Network点转化为边，无代码
- 这一题也算是最小割裸题，但是不够裸，做模板还是不太方便。
- 题意：去掉一些点使整个图不连通。问最少去掉多少个点。点的个数不超过50
- 题解（点一下）：点转化为边，无向图变有向图，权值为1，原边为INF，然后跑一下Dinic即可。如图：x'->y,y'->x转化为原边中的x->y,y->x@！
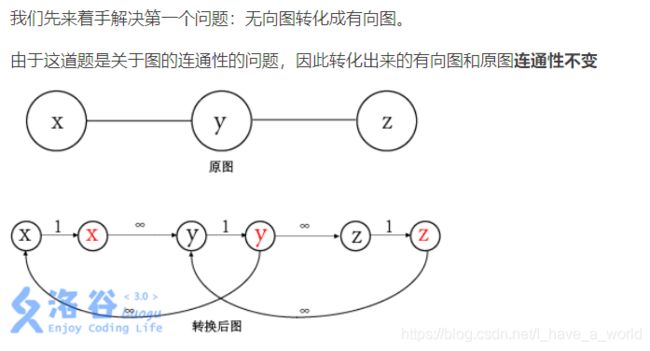
繁凡さん大佬总结的确实好，太全了吧：模板 - 最小割（常见最小割题型技巧总结）
4.费用流
1）最小费用最大流
概述：最小费用最大流——费用最小的最大流
操作：
- 只需要在EK/Dinic的操作中改一下增广路的顺序就ok了——每次增广花费最短的路。具体操作可以spfa，dijkstra。
- 一般不带负权，spfa，dijkstra都可以解决。带负权，就不知道怎么解决了emm（等遇到题目再说）
- Dinic也可以多路增广，按层数改为按最短路。注意当前弧优化不能想Dinic求最大流一样，因为这里的当前弧优化不想求最大流，它只会增，不会减（这里是凭记忆，具体也没太了解，甚至不知道说的对不对，总之注意）。
时间复杂度：（下面的代码就是基于此——类dinic模板）
模板：基于模板 - 费用流、最小费用最大流问题与算法实现（Bellman-Ford、SPFA、Dijkstra）（待修改、完善。因为还没有试过题目）
——修改1：基于个人ACM模板总结、Minimum Cost POJ - 2516 （费用流+EK+模板+分别建图）。还是EK模板香，方便操作，不容易出错。
ps：下一次学习基础知识，我可能会过的快一点了，甚至不在乎模板对不对，在正式使用中不断完善就ok了。
郑州大学铜牌大佬只学了EK_MCMF（最小费用流EK()），所以甚至金牌都不用所有算法都会，都够深入。我先拉进度，学最重要的，然后进行下一轮的突破（这一轮关于算法思想的积累，刷完kuangbin算完）
题目：传送门
#include
#include
#include
#include
#include
2）最大费用最大流——模板 - 费用流
边权改为负，然后跑最小费用最大流。这里应该就要注意spfa判负环了。
、、、、待完善。kuangbin专题，建议一题一题总结
