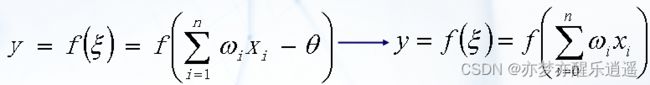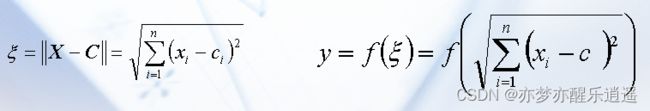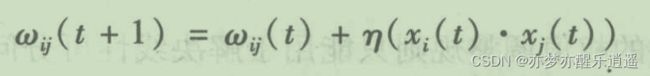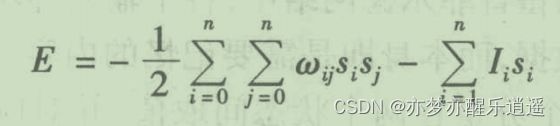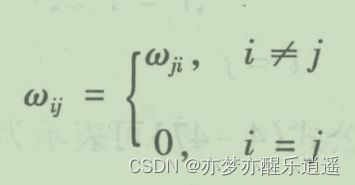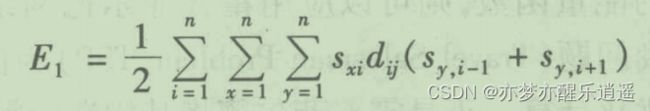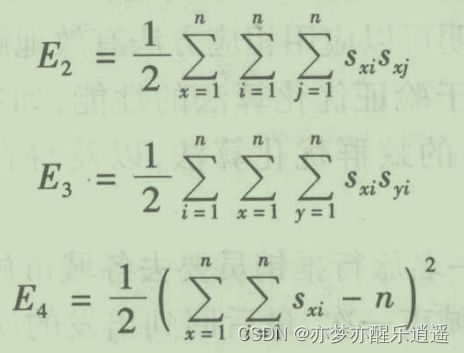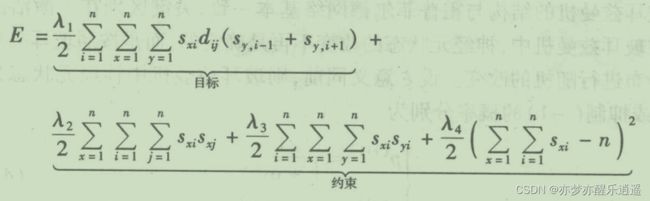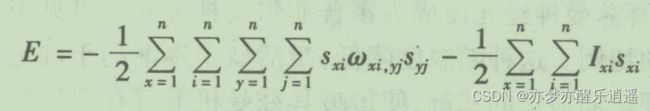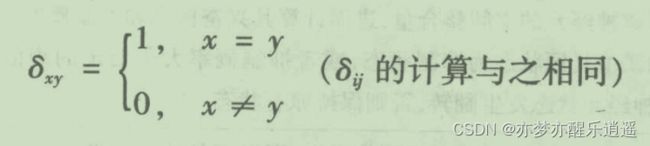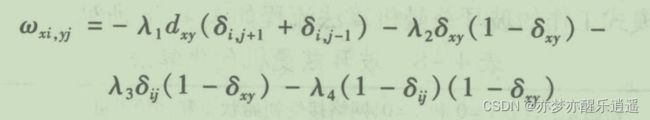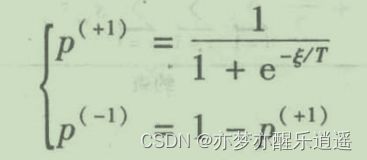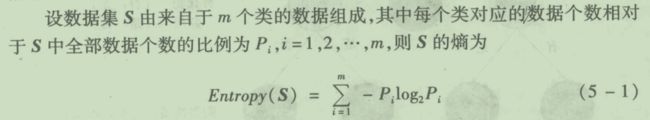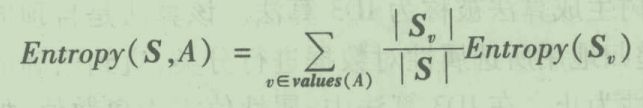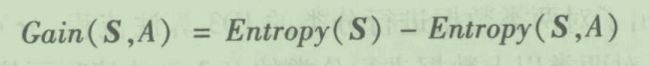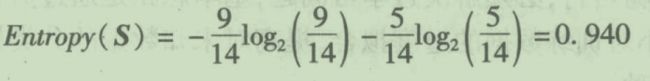人工智能导论笔记(持续更新)
文章目录
- 前言
- 人工智能概览
-
- 人工智能的概念
-
- 人工智能能做什么
- 强人工智能与弱人工智能
- 涉及领域
- 人工智能方法论
-
- 模拟层面
- 三大理念
-
- 符号主义
- 连结主义
- 行为主义
- AI研究领域全貌
- 人工智能主要理念浅析
-
- Learning(学习)
- 连结主义
- 符号主义AI
- 进化计算
- 群体智能
- 新兴智能
- 人工智能发展历程(待补)
- 搜索算法与问题求解
-
- 搜索概述
- 问题表示(表征)——状态空间/与或图
- 搜索——图(树)搜索
-
- 基本算法——以BFS举例
- 经典图搜索算法
- 盲目/启发式图搜索
- 对抗搜索(博弈搜索)
-
- Game Tree(博弈树)
- MiniMax algorithm
- α − β p r u n i n g \alpha-\beta \ pruning α−β pruning(剪枝)
- 蒙特卡洛树搜索(MCTS——Monte Carlo Tree Search)
- 知识与推理
-
- 推理概述
-
- 推理方式
- 推理控制策略——推理策略
-
- 推理方向
- 冲突消解
- 知识表示
-
- 知识的定义
- 知识的表示与推理
- 知识表示方法
-
- 一阶谓词逻辑表示方法
- 产生式规则表示法
- 语义网络表示法(知识图谱)
-
- 事物与概念的关系
- 用语义网络表示事实
- 情况与动作的表示
- 知识推理方法
-
- 经典逻辑推理
-
- 自然演绎推理
- 归结演绎推理
- 不确定性推理
- 模糊推理
- 人工神经网络
-
- 人工神经元模型
-
- 生物神经元
-
- 生物神经元的结构
- 生物神经元的功能
- 人工神经元
-
- 整合函数
- 激活函数
- 人工神经元互连模型
- 人工神经网络的拓扑结构
-
- 前馈神经网络
- 反馈神经网络
- 人工神经网络的学习方式
-
- 赫布(Hebb)学习
- 误差修正型学习
- 竞争型学习
- 随机性学习
- 多层感知机(误差修正型学习)
-
- 感知机阶段
- BP网络阶段
- 自适应线性神经元网络
- 径向基函数网络
- 霍普菲尔德网络与玻尔兹曼机(随机性学习)
-
- 霍普菲尔德网络——网络结构
- 联想记忆——训练算法
- 优化计算——解决最优化问题
- 玻尔兹曼机
- 自组织特征映射网(竞争型学习)
-
- 灵感来源
- 网络结构
- 训练方法
- 理解与总结
- 机器学习
-
- 主要策略
-
- 机械式学习
- 指导式学习
- 类比学习
- 解释学习
- 归纳学习
- 类比学习方法
-
- 属性类比学习
- 转换类比学习
- 基于解释的学习
- 规则集的归纳学习
- 决策树学习
-
- 决策树
- 决策树构建(ID3算法)
-
- 宏观思路
- 信息熵与属性选择
- 例子
- 决策树剪枝
- 贝叶斯学习
- 聚类分析
前言
初学者往往对人工智能的认识不够广泛,往往就集中于深度学习这一块,在学习一段时间后再回头重新学习导论,用高屋建瓴的视角俯瞰自己曾经学习的领域,对以后的研究方向有很大的好处。
本文脱胎于 刘峡壁的《人工智能:方法与系统》,这本书比较老,但是我们要的就是这种有年代的书,因为现在的书大部分都是以深度学习为主的,而如果要全方位认识人工智能,致力于搞科研,这种古老的体系化知识是很有必要的,毕竟要触类旁通还得广泛学习。
人工智能概览
人工智能的概念
严格来说,要给人工智能下定义不是一件容易的事情,毕竟人类自己都没有认清自己的智慧,所以人工智能更多的是各种假说,没有统一的严格定义。
人工智能能做什么
人工智能并非无所不能,事实上,从最开始人们通用人工智能的宏图伟业开始,人们不断受到打击,最终将注意力集中于模式识别上。模式识别专注于一个特定的任务,比如图像识别等。
从小到大来说,人工智能可以完成如下任务,或者说,有如下能力的就可以成为智能:
- 感知。深度学习有一个巨大的领域就是CV,计算机视觉有三大顶会,CVPR,ICCV,ECCV。另一个领域就是NLP,自然语言处理,也同样有顶会ACL。
- 行动。行动其实也可以理解为决策。
- 推理。推理是一种高级的智慧,现在没有任何一种人工智能能够实现真正的推理,尤其是因果推理。
- 通用任务。这一点是一个质变,也是现在人们着力解决的
- 真正的学习能力。
- 社会性。
- 创造力。
现在的人工智能还很笨,随着未来不断研究至创造力,人工智能就真的和人一样了。说实话,我感觉达到推理和通用任务的地步就行了,否则我真的怀疑人类是否会被人工智能推翻。
强人工智能与弱人工智能
说实话,现在的人工智能识别个猫猫狗狗都费劲,很明显都是弱人工智能。

图灵设计了图灵机架构,是当之无愧的计算机之父。而图灵奖也是当今计算机最高奖项,类比于诺贝尔奖,菲尔兹奖。
关于人工智能的定义,图灵在《Computing Machinery and intelligence》中给出一个假设,如果通过了图灵测试,那么计算机就可以被认为是具有人类智能。
这种观点,注重人工智能的实用性,表现。
只要表现得和人一样就行,不需要管背后是否由推理逻辑支持。因此被称作“弱人工智能”
由此,中文房间的观点被提出,如果房间里的智能体对知识并没有理解,只不过通过各种资料进行key:value的比对做出响应,那并不是真正的智能,即使是和人表现一样。这就像一个只会背答案的考生,虽然他把所有答案背会了,每次都能100分,但是他没有学会知识。
这种观点更关注智能的内核:逻辑推理,是“强人工智能”
两种观点我觉得不冲突吧,并没有争议,只是注重的点不同,人们最先实现的肯定是图灵智能,之后发展的更好才能实现中文房间级别的智能。
涉及领域
人工智能是一个广泛的领域,交叉的领域。
偏向生物的,有认知科学,脑科学。
偏向控制的,有机器人,模式识别,智能控制。
其他的,包括但不限于NLP,CV,计算机博弈,自动定理证明,人工神经网络,专家系统,等。
人工智能方法论
模拟层面
本质上,人工智能就是用人工制造的智能体去模拟实际的智能。
那模拟的方面就有很多:
- 神经层面。用生物的方法去真正地模拟神经元。
- 神经模型层面。将神经元模型简化为数学模型,从而构建神经网络。现在最流行的深度学习就是使用 σ ( w T x + b ) \sigma(w^Tx+b) σ(wTx+b)这种线性模型+激活函数的简化思路,更复杂的有脉冲神经网络的LIF模型,对神经元的模拟程度更高。
- 认知层面。这一层面对人的思考过程进行假设,抽象,和符号主义联系较大。
- 行为层面。这一层面只要保证智能体表现出像人一样的行为即可。
- 目标层面。这一层面只要能完成任务就好,什么方法都可以用,比如最优化,线性规划之类的非人方法。
三大理念
符号主义
用符号表达式表达知识,并且通过符号实现推理,认知。
符号主义认为,将物理模式或者符号转化为其他模式或者符号,这样的系统就有可能产生智能。
符号主义中的专家系统,其核心就是离散数学中的一阶逻辑,想想你当年学离散数学时看过多少符号吧,叫符号主义似乎也很合理了。
符号主义是最开始人们的理念,也是一个非常宏观的理念,后来发现走不通,于是开始走神经网络,现在神经网络这块又块走到头了,于是就又把视线投向了符号主义,其中脉冲神经网络也和符号主义有比较大的关系。
连结主义
现在主流的深度学习就是连结主义。
关键在于,节点模型,连接模型,训练算法。
行为主义
行为主义发源于控制论,强化学习就是行为主义的体现。
行为主义着重于行为,智能体做出行为,影响环境,智能体收到反馈,调整状态,进行下一步行动。如此将经验积累下来,构成最终的智能体。
在维基百科中是这样介绍强化学习的:强化学习(RL)作为机器学习的一个子领域,其灵感来源于心理学中的行为主义理论,即智能体如何在环境给予的奖励或惩罚的刺激下(即与环境的交互中),逐步形成对刺激的预期,产生能获得最大利益的习惯性行为。它强调如何基于环境而行动,以取得最大化的预期利益。通俗的讲:就是根据环境学习一套策略,能够最大化期望奖励。由于它具有普适性而被很多领域进行研究,例如自动驾驶,博弈论、控制论、运筹学、信息论、仿真优化、多主体系统学习、群体智能、统计学以及遗传算法。
AI研究领域全貌
这个图稍微有点老,现在有很多新东西了。
人工智能主要理念浅析
Learning(学习)
学习意味着变化。虽然这句话听起来像废话,但是至少说明了学习是一种积累的过程,而非直接灌输。
这张图并不全面,实际上只是强化学习的学习流程,而深度学习之类的梯度下降学习和这个还是有很大差别的。
- 学习更多的任务
- 把已经学会的任务变得更好(比如提高准确率)
- 加速已有任务
之后就是产生,这个可以理解为创造。
学习还可以分为监督学习,非监督学习,半监督学习,强化学习。
监督学习其实是合理的,因为平时我们学东西也是有老师的,但是这样的代价比较大,能取得好的效果也是应该的。
非监督学习更多的是自发寻找分类,自发进行聚类,本质上,就是我即使不知道你是什么,但是我明白你们和他们并不一样,只需要能认识到区别,那就可以聚类。
半监督学习是折中。半监督学习采用大量的低成本的无标签数据+少量高成本标签数据,先用标签数据训练模型,再用模型在无标签数据上跑,其中必然有把握大的数据( P → 1 P\rightarrow 1 P→1),把这些无标签数据放到标签数据中,然后用新的标签数据训练新的模型,如此循环,直到无标签数据消耗完毕,标注+训练的任务就都完成了。
强化学习的经典过程如下图。
评估机器学习的效果,涉及到过拟合欠拟合,偏差,方差,鲁棒性,可解释性,计算复杂度(训练成本)。
连结主义
发展模型:
- M-P模型
- 感知机
- Hopfield Model,B-P学习方法
- 深度学习(Jeoffrey Hinton)
现在深度学习是连结主义最流行的方法,核心的主题有两个:
- 拓扑。这个可以理解为网络模型
- 算法。这个可以理解为建立在网络之上的训练算法
我研究的领域是以脉冲神经网络为代表的类脑智能。类脑智能的前景我觉得还是不错的,是一个很有意思的领域,其最佳的运行平台是类脑芯片。
符号主义AI
符号主义是人工智能最初的主流,大家刚开始的志向是很远大的,直接干通用人工智能。后来发现干不动。
符号主义最开始是特定问题解决,之后发展专家系统,然后是知识工程,最后就是常识。
进化计算
进化计算的思路来源于达尔文进化论,最优化中的遗传算法就是这种思路。
群体智能
蚂蚁和鸟类,其单体的智能很有限,但是其群体可以体现出一种较高的智慧。
群体内部的成员相互影响,最后表现出智能,和连结主义是有一点隐晦的联系的。
群体智能的领域如下:
- 多智能体系统(Multi-agent)
- 蚁群算法(ant colony)
- 粒子群算法(particle swarm)
新兴智能
这里的新兴是相对于传统的符号主义的。
比如行为主义,强化学习。
人工智能发展历程(待补)
搜索算法与问题求解
人工智能最开始是为了通用问题设计的。通用的问题没有具体的步骤,但是一般来说都是有一个可能性的解空间的,所以人们最开始是以搜索算法来实现人工智能的。
搜索概述
学人工智能之前,一般都已经学过算法了,经典的迷宫问题,BFS,DFS,都是搜索的范畴。
搜索需要考虑两个点:完备/有效(Completeness/Effectiveness),效率(Efficiency),然而这两个点是冲突的,想要好的结果,往往效率较低(效果最好的必然是遍历),效率高的,往往容易漏过很多搜索空间。
基于这两个点,产生很多概念:
- 完备性(Completeness)。如果问题有解,算法必然能找出解
- 最优性(Optimality)。必然找出最优解
- 复杂性(Complexity)。时间复杂度和空间复杂度。
- 盲目搜索(Blind search)与启发式搜索(Heuristic search)。盲目搜索算法与问题本身无关,而启发式搜索利用问题本身的信息制导搜索的方向。
- 局部搜索(Local search)与全局搜索(Global search)。局部搜索不会考虑全局信息。
- 可行解(Feasible solution)与最优解(Optimal solution)。
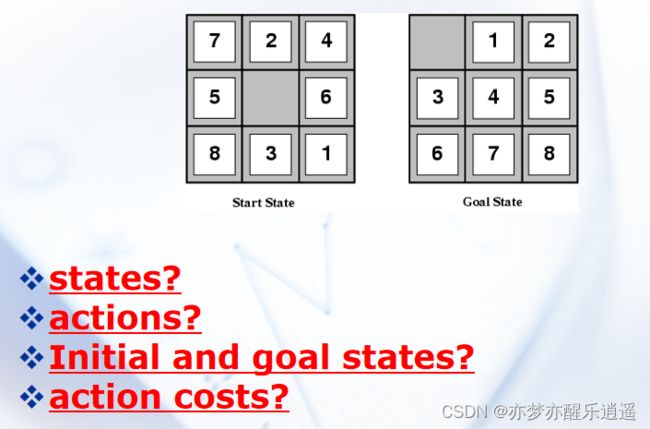
问题的求解一般分为如下几步:
- 表示问题。比如思考如何表示问题的状态,起始状态,最终状态
- 构思搜索方式与状态转移公式。
- 表达状态空间,进行搜索。
问题表示(表征)——状态空间/与或图
问题表征是求解的第一步。有两种求解思路:
- 状态空间表示法。将所有状态表示为节点,通过状态转移找到从起点到终点的路径
- 与或图法。与或图的每一个节点都是一个问题,把问题表示为节点,通过与/或关系拆分简化问题(这和解空间完全是不同的概念,虽然两者都可以用树表示)。与节点,其子节点全部成立,根节点才成立。或节点,其子节点成立一个,根节点就成立。
拿汉诺塔问题举例,通过与节点解题。
首先用三元组表示问题状态,之后给出第一个问题:(111)->(333)
之后将这个问题拆分成三个步骤,如果这三个步骤全部可以实现,那么问题就能解决。
之后继续递归拆分问题,直到所有叶节点都可以解决,则最大的根节点就可以。
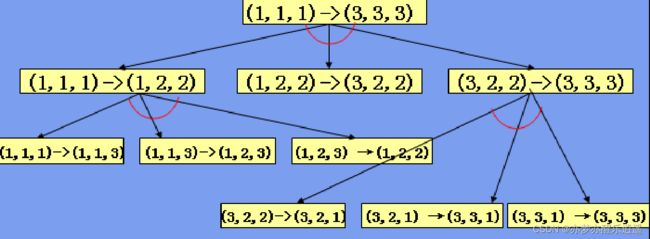
搜索——图(树)搜索
无论是状态空间还是与或图,都是图形式,所以解决问题的算法可以统称为图搜索。
基本算法——以BFS举例
BFS是典型的搜索算法。
Open表就是那个队列
Close表可以用vis数组来标记访问
之后每次取出一个节点,进行访问,之后把周围的节点放到队列(Open表)里。
下图给出一个BFS的执行过程。
经典图搜索算法
在图搜索中,盲目搜索与启发式搜索的区别在于选择节点放入Open表的一步。选择什么样的节点,选择策略就决定了算法属于盲目还是启发式。
盲目/启发式图搜索
广度优先和深度优先,以及这两者的折中——深度有限算法,都是盲目搜索,盲目搜索不利用问题本身的特征
解决所有问题都是用一模一样的步骤。
而启发式搜索,在扩展节点的时候会用一个函数进行节点评估,选择最有利的或者损失最小的一部分节点进行扩展。
启发式搜索的评估函数有两种,A*算法以及AO*算法。
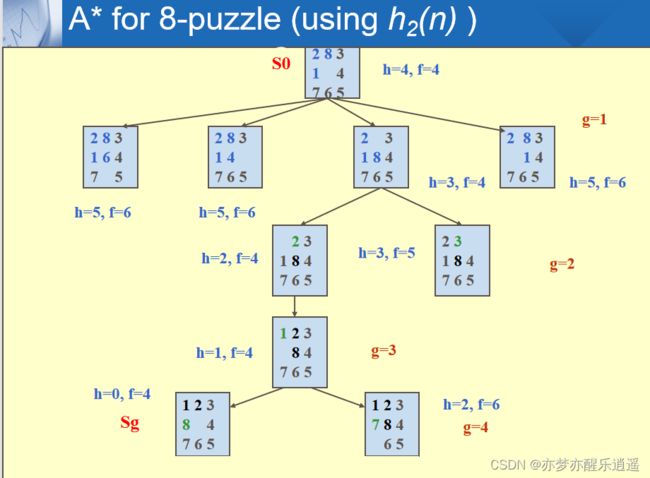
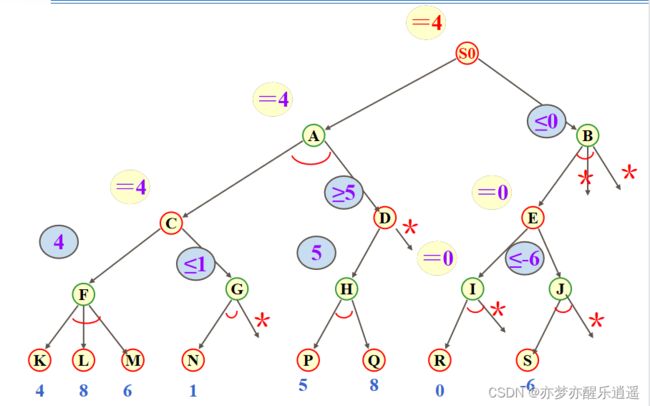
下图是A*算法,这个算法中 f(n)=g(n)+h(n)
g(n)是从0走到n步已经付出的成本,h(n)是从n步走到目标需要付出的成本,两个成本加起来就是从头到尾的成本。
很明显,h(n)是一个启发式函数。

进一步举例S0是当前,Sg是目标。有两种启发式函数:
h1是当前状态和目标状态之间的差异,图中为128三个块。
h2计算曼哈顿距离,同样是利用差异,但是考虑到了差异的大小,对128三个块进行求解,8这一块的曼哈顿距离为2,所以综合为4。
对抗搜索(博弈搜索)
通常指2人零和博弈,所谓零和,就是两个人,一个叫Max,一个叫Min,他们的数值和固定,一方赢另一方必然输。
Game Tree(博弈树)
零和博弈假定两人是理性的,每一步只采取最当前有利的措施,即贪心。
因为信息完备(双方没有隐瞒),所以一个博弈从一开始就可以预测到结果,因为每一步都可以推理出来。推理过程就可以用博弈树。
用分硬币游戏举例。
两人轮流将一堆硬币分成大小不等两堆。最后无堆可分者输
这里只是简单给出所有可能的发展方向,不涉及到分支的贪心选择。不过如果下棋的时候,对面的人拿着一个博弈树对比你的步骤,那你基本是赢不了了。
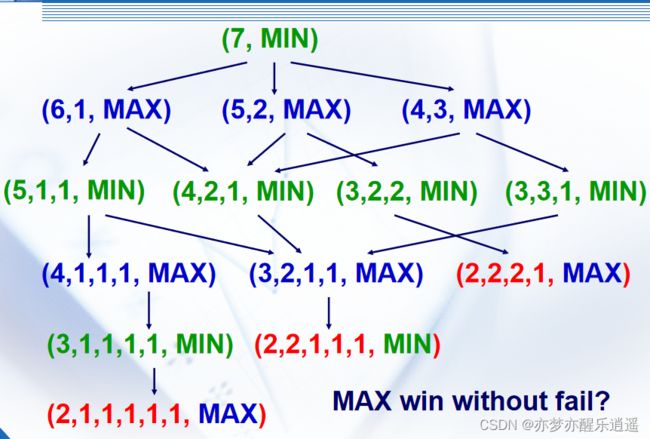
回头看,博弈树实际上也是与或图。在自己的分支上,只要有一个分支成功就可以走,但是考虑另一方分支,需要让所有分支都失败。(存疑)
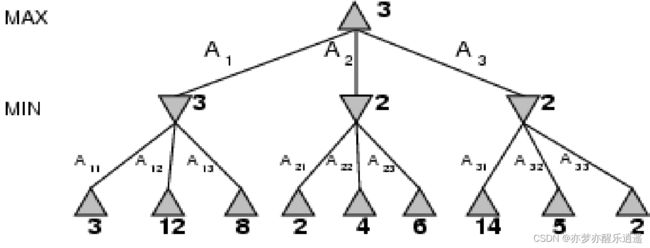
MiniMax algorithm
虽然博弈树可以直接推到结果,但是搜索空间太多,需要限制深度,选择次优策略。
次优策略中,选择步骤需要用到评估函数,
子节点值是会向上传播的,但传播原则对Max和Min来说是相反的。
对Min来说,需要选择子节点中最小的值,Max选择子节点中最大的值。
评估函数暂且不谈,先说对称状态冗余,下面的四种情况实际是一种情况,在博弈树中就只保留一种考虑。

下图是第一步决策,叶节点的评估函数如何计算我也不太清楚,但是从叶节点向中层的传播是Min传播,所以都选择最小的传,从中层像根节点传播的时候是Max传播,所以用最大的传。
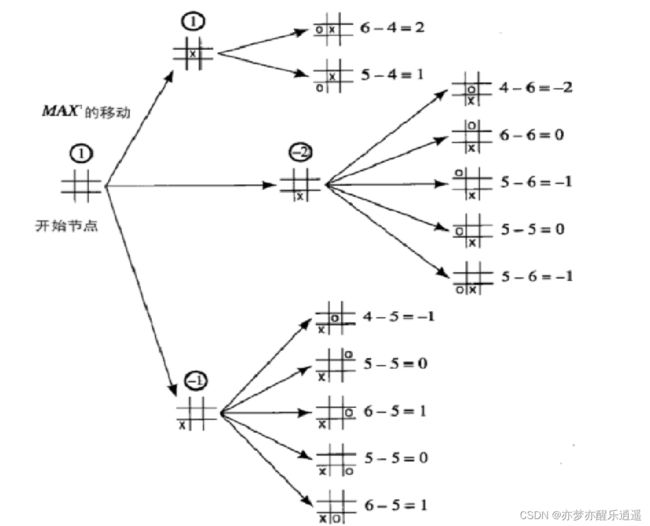
之后就是走两步,具体是以什么原则走的我也不太清楚,但是走了两步以后,又是一轮新的博弈,传播原则还是这样。继续走两步,走两步,结果就出来了。
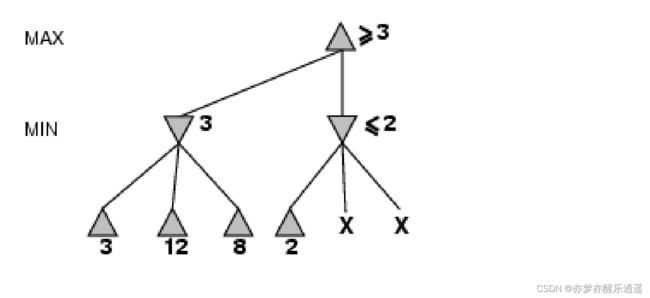
α − β p r u n i n g \alpha-\beta \ pruning α−β pruning(剪枝)
在博弈树的判断中,因为要选择最大最小,所以是可以剪枝的。
下图中,Min节点中有3,说明Max节点至少是3。
另一个Min节点的叶节点出现2,说明Min节点最大就是2,那么Max节点不可能选择这个Min节点了,所以没必要去扩展这个Min节点了。
上面的例子只有两层,这里多看两层,剪枝的力度是更大的。我按照12345层来叙说,第四层出现4节点,又因为G节点最大1,所以C就是4,因为A节点是Min节点,所以A最大是4。这时跳到另一个节点,发现D节点最小是5,所以A就是4。同理,B节点最大是0。S0节点是Max节点,所以B直接剪枝。
我讲的思路比较随意,真正执行起来必然是有一个顺序的。但是剪枝的思想如此。
蒙特卡洛树搜索(MCTS——Monte Carlo Tree Search)
蒙特卡洛树搜索是一种启发式搜索。
核心在于,如何从待扩展节点中,找出最有潜力的节点,从而让树朝着好的方向生长?
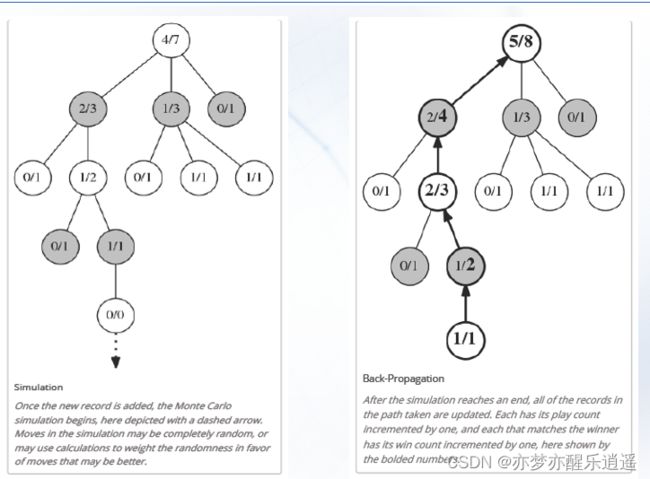
这就涉及到模拟,所谓模拟就是从这个节点开始,按照某种原则一条路走到终点,路上不进行分叉,到终点以后回传信息,更新节点状态。这样做的成本很低,因为不分叉。
节点状态中的信息代表了节点的潜力,潜力实际上可以理解为节点能成功的概率,选择的时候就可以根据潜力进行选择。

举个例子,首先从上往下找成功率最高的节点,找到了第四层的1/1节点,从此开始生成子节点,进行模拟。
来到第二幅图,模拟的结果进行回传,更新路径上所有的考察值。
后续进行下次选择时,如果这条路上成功率增加,后面会继续选择这条。反过来,如果反复失败,成功率就会下降,直到不选择这条路为止。
知识与推理
知识表示与逻辑推理是符号主义的重点。
推理概述
推理方式
按照推理的逻辑基础分:
- 演绎推理。三段论严格推理,本质上只是现有知识的挖掘。
- 归纳推理。从个体到一般,虽然不一定准确,但是和人的推理机制有共同之处,可以创造新知识。
- 默认推理。又叫缺省推理,在条件不足(知识集不完备)的情况下,对条件进行假设,再加以推理。
按照确定程度分:
- 确定性推理。结果只能是真/假(0,1)
- 不确定性推理。结果是概率
按照推理过程的单调性分:
- 非单调推理。有时候推着推着会发现结论错误,这时会选择回滚,删除,否定前面的推理,重新来过。
- 单调推理。结论只增加不减少
推理控制策略——推理策略
推理控制分为推理策略+搜索策略。推理策略控制推理方向,搜索策略负责具体求解。由于知识表示可以用图来表示,所以搜索策略可以用前面的搜索技术,所以这里只解释搜索策略
推理方向
- 正向推理。正向推理,不管我要什么,反正先全部推出来,最后从结果里找。
这样往往容易得出大量结论,但不够精准 - 逆向推理。构建假设集,刚开始只有结果一个,然后逆向找条件,加入假设集,重复直到所有需要的知识都可以在知识库里找到。
- 双向推理。结合
冲突消解
同时有多个选项可以选择,选择哪个就是冲突消解的范畴。
冲突消解有一大堆原则与算法,但是总的来说,最终目的是提高推理效率。
知识表示
知识的定义
知识如何定义还没有一个定论。
知识和信息的区别,我认为是是否经过加工,是否能用于推理。你学到的东西就是知识,是加工过的,而你知道的,或者简单背会的,是信息,很多信息不可以直接利用。
AI知识的概念从何而来?早期符号主义AI致力于解决通用问题,但是能力很差,所以AI着眼于专业问题,专家系统与知识的概念应运而生。
随着知识领域的研究加深,知识工程这个大领域形成
这个系统包含了从表示到获取,推理,利用,储存等一系列过程。
知识的表示与推理
知识的表示应该具有如下特征:
- 表征能力。能不能表示好知识的含义
- 可利用性。方不方便计算机推理
- 可组织性与可维护性。这一点主要考虑到了知识增长的过程
- 可实现性。
- 自然性与可理解性。前面主要是针对机器的,这一点要针对人。
知识表示与推理大致有三种:
- 逻辑表示与推理
- 规则表示与推理
- 基于语义网络的概念表示
知识表示方法
一阶谓词逻辑表示方法
这个参考离散数学中的一阶逻辑。
相关概念:
- 命题与谓词
- 连接词(非 析取 合取 蕴含 等价)与量词
- 谓词公式
用一阶逻辑表示现实世界中的各种信息,之后的推理反而是很好做的,就是离散数学,难点在于表示。
优点:
- 自然,人可以看懂
- 明确,精确,模块化,便于推理(这是离散数学的优势)
- 灵活。把知识表示与逻辑推理分离(我个人感觉,把记忆和推理分开或许不是一个好的思路,人脑很明显就不是这样的,而且看现在的冯诺依曼架构,分的很开,但是反而没有那么灵活,只是便于开发罢了)
缺点:
- 僵硬。离散数学相比于人类的语言,表达能力还是差很多。
- 知识库难以管理。命题逻辑不容易组织
- 组合爆炸。逻辑推理没有好的启发式算法,所以多是盲目推理,当基础知识增加,结论就会爆炸
- 系统效率低。推理的过程仅仅是用命题演算,不会考虑知识本身的含义。
产生式规则表示法
发源于博斯特机模型。
产生式表示法可以表示事实+规则。可以描述确定性事实,也可以描述不确定性事实。
- 事物属性。(对象,属性,值)三元组
- 事物之间相互关系。(关系,对象1,对象2)三元组
- 不确定事实。增加一元概率,比如(对象,属性,值,概率)
产生式规则也很简单,仍然是IF P THEN Q,满足条件就得出结论。
产生式规则的推理方法和命题逻辑是一样的,都是前提与结论,但是还是有一个重大区别:不确定性
产生式规则的前提和结论都可以附加概率,而命题逻辑就是完全精准。
优点:
- 语言接近自然语言
- 表达的能力较强,兼顾概率
- 表达的形式较为固定(三元组,四元组),可以统一处理
缺点:
- 效率低。推理的前提是匹配条件,匹配本身就是一种搜索,涉及到遍历,效率就低。
- 不能表示结构性知识。因为三元组表示格式固定,而且三元组之间不能相互调用,就没办法产生结构型网络型,有层次的知识。
这里举一个产生式系统的例子。
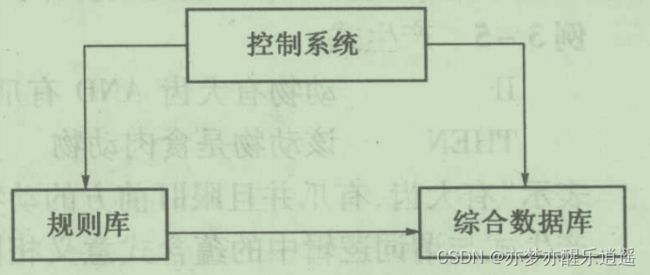
Mycin是第一个比较清晰的专家系统。
规则数据库储存知识,全局数据库储存动态的中间结果。
推理的过程类似于广度优先搜索,或者说是离散数学里的命题推演。
首先用已知条件推理一些结论,然后用新的结论+已知条件重新推理
推理的过程中处于效率考虑,推理过的就不推了
直到最终所有结论都无法推理出新的结论
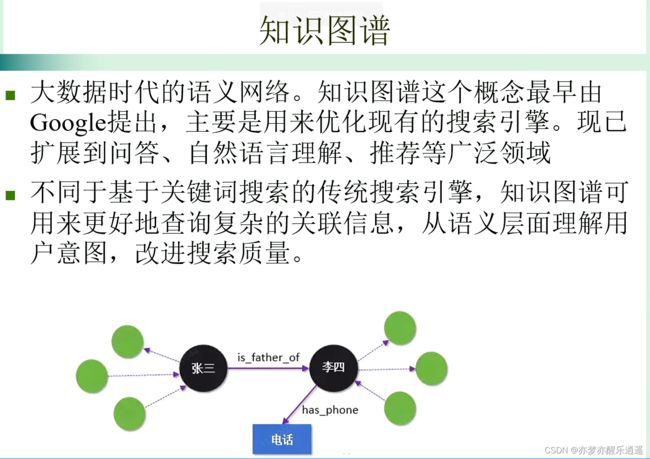
语义网络表示法(知识图谱)
前两种表示方法,其实和人类的记忆与推理还是有比较大的出入的,人类的下意识推理更多的是一种联想,前两种并没有表示出知识之间的连接关系。
语义网络是基于人类联想记忆的心理学模型,认为记忆是由概念间的联系实现的,比如睹物思人的感觉。之后这个模型就被用于nlp中。现在语义网络被广泛运用。
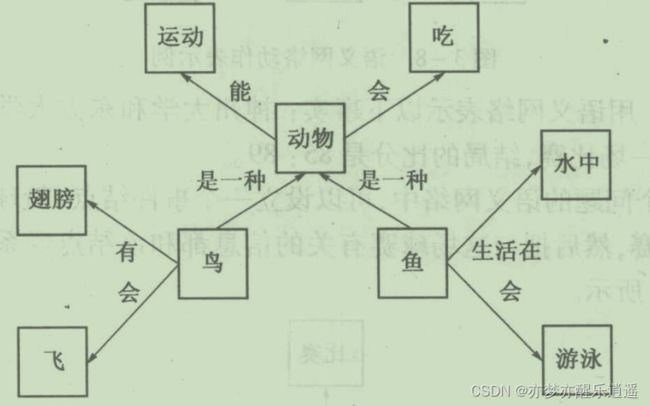
语义网络是一个有向图。节点是实体,可以表示事物,概念,情况,属性,状态,事件,动作等,连接弧代表实体之间的语义联系。
语义网络从另一个角度看,也可以看做由一系列语义单元构成,两个节点+一个弧就是一个单元,一个单元是一个三元组(顶点1,边,顶点2)

语义网络可以描述任意复杂关系,但是复杂关系本身是由一系列基础的语义单元组合而成。而常用的基本语义关系包括亲属,包含,属性,时间,位置,相近,推论等。
语义网络的优点:
- 结构性。把事物之间的联系显示地表示出来,而且节点还可以进行继承之类的操作,实现信息共享。
- 联想性。便于进行联想
- 自索引性。不需要遍历就可以找到与节点相关的关系,有效避免组合爆炸问题。
- 自然性。符合自然知识结构
缺点:
- 非严格性。推理不能保证正确性。说实话我觉得不是缺点,人的推理本身也不能保证此次正确,不确定性正式人的智慧来源(个人拙见)
- 复杂性。灵活,同时带来复杂。
接下来举一些语义网络表示复杂关系的例子:
事物与概念的关系
(事物,边,属性),这种语义单元常用于表示属性,特性。
用语义网络表示事实
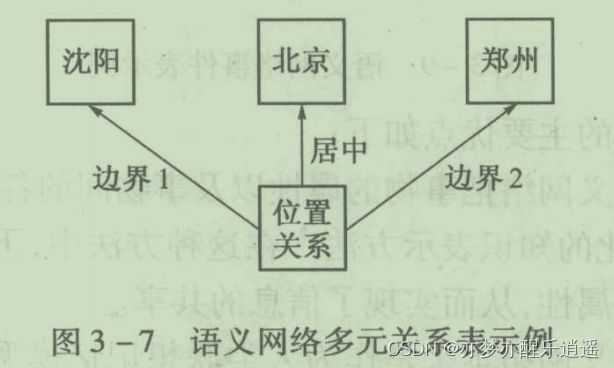
北京位于沈阳和郑州之间。这是一个多元关系,需要引入位置关系的顶点,然后加上三条边就可以表示一个相对位置的事实。
情况与动作的表示
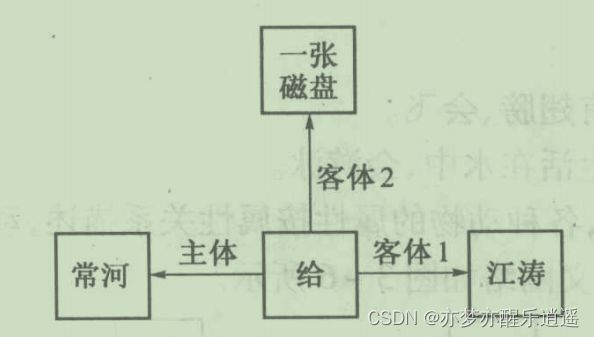
引入情况节点和动作节点,可以更好的表示情况与动作。
长河给江涛一张磁盘。给节点就是一个动作节点。
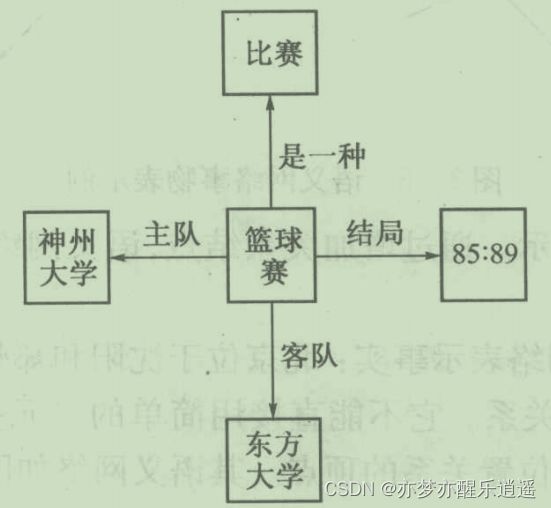
神州大学和东方大学两校篮球队在东方大学进行一场比赛,比分是85:89。篮球赛节点是一个事件节点。
知识推理方法
经典逻辑推理
经典逻辑推理基于离散数学的一阶逻辑。
自然演绎推理
自然演绎推理就是经典的命题演算,正向推理,优点是过程自然,逻辑简单,缺点在于容易产生大量的中间结果,导致知识爆炸(参考BFS)。
归结演绎推理
归结法就是反证法。鲁滨逊归结原理也叫消解原理。
人工智能的很多问题可以转化为定理证明问题,要想证明 P → Q P\rightarrow Q P→Q是永真,只需要证明 ¬ ( P → Q ) \lnot(P\rightarrow Q) ¬(P→Q)即 P ∧ ¬ Q P\land \lnot Q P∧¬Q不存在即可。
海博伦理论提供了理论基础,鲁滨逊归结原理提供了实现条件。
具体过程比较复杂,姑且当消解看就行了。
不确定性推理
不确定性的五大基本问题:
- 不确定性的表示与度量
- 不确定性知识的匹配
- 不确定性的传递
- 组合证据的不确定性
- 结论不确定性的合成
其中,不确定性的传递是不确定性推理的本质和核心问题,而不确定行的表示与度量则确定了基本的推理方法。
模糊推理
未写
人工神经网络
人工神经网络隶属于连结主义。因为我是搞SNN的,所以我会着重描述这一章。
人工神经网络是在神经元的级别上模拟,试图从结构上的模拟实现功能上的模拟。
连结主义和符号主义区别还是很大的,符号主义基于人类研究出的逻辑学,自顶向下,连结主义先构建底层结构,试图模拟出智能。
连结主义的两个核心问题:
- 网络模型。构建网络结构,并且实现输入到结果的输出。
- 学习算法。如何自动确认或者调整神经元之间的权值使得效果提升。
这两个方面是紧密连接的,网络模型基本决定了学习方法的大方向。
人工神经元模型
生物神经元
生物神经系统包括神经元和胶质细胞。胶质细胞数量远大于神经细胞,但是人们认为神经细胞发挥了主要作用,胶质细胞仅仅是起到了辅助作用。关于胶质细胞,我分享过一篇论文:
【论文分享】脉冲神经网络之间的信息传递与类比学习,基于星形胶质细胞
为了区分,通常把物理上的神经元叫做生物神经元,人造的叫人工神经元。
生物神经元已经表现出了兴奋,传导,整合的能力,因此人工神经元也在模仿这些已经被观察到的能力。
神经元的个数与智能水平是正相关的,比如海马是2000个神经元,人则有 1 0 12 10^{12} 1012个神经元。我们常常说现在的神经网络太过庞大,训练成本太高,但是人脑中也有这么多神经元,所以网络做大肯定是没有问题的。
目前的SNN可以用更少的神经元表示出与ANN不遑多让的性能,并且能耗更低。未来SNN的方向,肯定是要把网络做大,脑区分开,协作,形成一个整体。但是有一个问题就是学习算法太匮乏了,STDP虽然有效,但是可能并不一定是最好的,切不可迷信STDP,要有自己的想法,未来说不定会出现新的学习方法,说不定就是你自己亲手创造出来的呢,现在才大学本科,一切皆有可能。
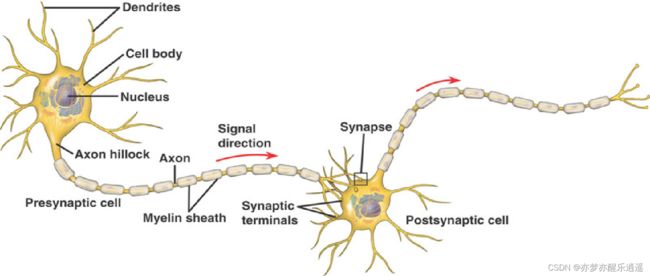
生物神经元的结构
生物神经元在形状和大小上多种多样,但是在组织结构上具有共性。
总的来说,基本就是树突(输入)+胞体(处理)+输出(轴突)
- 树突。胞体向外延伸的,除轴突以外的所有分支。长度短,但是数量多,用于接受其他神经元的输入。
- 胞体。本身是一个细胞,主要表现就是膜电位的变化。
- 轴突。轴突是向外延伸的,最长的神经纤维中的一支(只有一支吗?),轴突末端分叉(可以与多个神经元相连吗?),与树突连接,连接部位就叫突触。
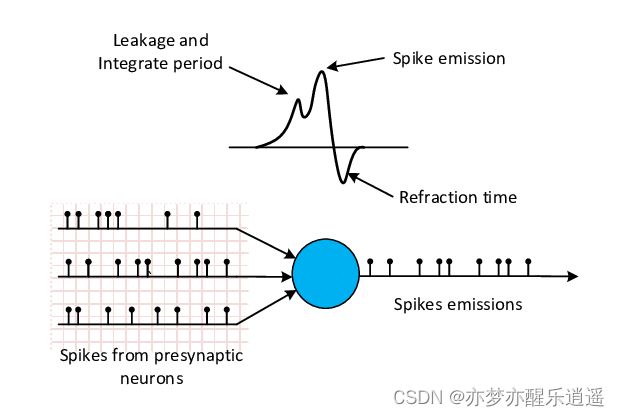
生物神经元的胞体工作原理:
回顾一下高中生物,细胞体一般内部电位低于外部电位,电位之差称作膜电位。
没有信号输入的时候是静息电位,信号的输入会使电位提升,但是膜上的电位也在逐渐泄露,如果长时间不输入,最后又会跌回到静息电位。
如果信号持续输入,随着信号的输入,整合,积累,膜电位越来越高,直到突破阈值电位。
突破阈值电位后,膜电位会急剧上升,然后快速放电,生成一个电脉冲,将信息通过轴突输出到其他神经元。
生物神经元的功能
目前已有的研究,已经发现了神经元有如下表现:
- 时空整合功能。时间指的是 ,神经元可以接受来自于同一突触但是不同时间的脉冲。空间指的是,神经元可以接受来自于同一时间不同突触的脉冲。时空的整合为神经元处理时空信息的能力打下基础。
- 兴奋和抑制。神经脉冲并不是直接传导的,而是类似于神经递质,通过权值或者是其他方式传导的,所以既有兴奋,又有抑制,就如同神经递质一样。
- 脉冲与电位转换。电脉冲可以通过神经递质转化为膜电位,膜电位可以通过激发产生脉冲。膜电位代表连续信息,电脉冲代表离散信息,连续和离散的转换有点像模数转换。本质上是量子级别的转换,关键在于神经递质的效果就是量子化学效果。(怎么扯到了量子了)
- 神经纤维传导速率。神经脉冲在轴突上传导是有速度的,如果髓磷脂比较多,传导速度可以达到100m/s,没有髓磷脂的可能只有5m/s
- 突触延时与不应期。不应期看起来是没什么用的,但是或许有用呢?
人工神经元
最开始的人工神经元是M-P神经元,M指神经生物学家McCulloch(麦克洛奇)P指数学家Pitts(皮茨)。
他俩构建了MP模型,写了篇论文《McCulloch, Warren S., and Walter Pitts. “A logical calculus of the ideas immanent in nervous activity.” The bulletin of mathematical biophysics 5.4 (1943): 115-133.》,这个论文可以说是连结主义的开山之作。
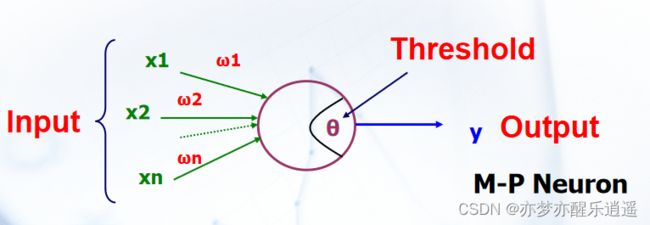
M-P模型其实就是现在深度学习用的基本结构,输入一个向量,通过权值整合后激活(激活函数又被称作转移函数和信号函数)。
整合函数
最经典的就是加权求和,现在用的也是。为了简化公式,把 θ \theta θ超参数作为 x 0 x_0 x0。
但是整合不仅仅有这一种,还有一种径向距离函数。
前面的超参数向量是作为加权了,这里的超参数向量被用作欧氏距离比较,X与C偏离越大,整合后值就越大。
相比于前面的X越大,整合后值越大,感觉还是有共通之处的。
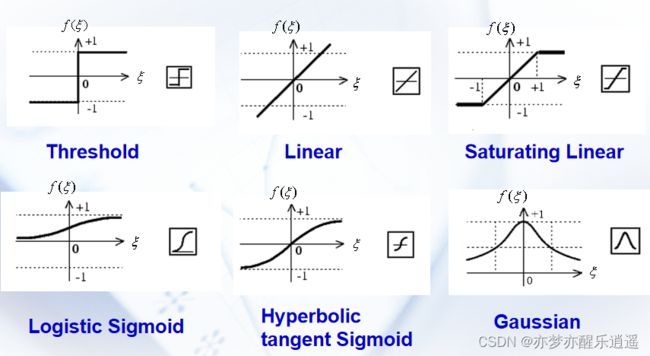
激活函数
激活函数一定是非线性的。如果用线性激活,那么无论堆多少层,和一层的效果都是一样的。当然,这个是后话了。
线性在这里也被列出来了,我猜测是因为径向距离好像还不是线性的,所以应该也能配套。但是需要明确的是,整合与激活中,一定要有一个非线性。
这些激活函数中,sigmoid,ReLU(以及Leaky ReLU),tanh用的比较多,其他的较少。
不过阈值函数比较有意思,这个就有点激发,脉冲的感觉了。
人工神经元互连模型
生物中,一个轴突可以连到多个神经元,一个神经元也可以接受多个轴突的输入。计算机中模拟会做一些简化,比如全连接之类的。
这种输入输出的数量反映到到计算机中就是输入向量与输出向量的长度。比如一个神经元接收n个输入,同时输出到m个神经元,那么输入向量长度就有n,输出向量长度为m。
人工神经网络的拓扑结构
全连接只是一种基本的连接方式,实际上,在大脑中,神经元的连接方式是千变万化的,所以就产生了各种网络拓扑结构。
大致分类:
- 前馈神经网络(静态网络)。没有回路
- 反馈神经网络(又叫动态神经网络或者循环神经网络)。有回路
- 侧抑制型网络。同层神经元有侧抑制连接
- 反馈型网络。不同层神经元之间存在反馈连接
前馈神经网络
如左图,最开始学的神经网络就是前馈神经网络,不存在回路,只是从前往后传。
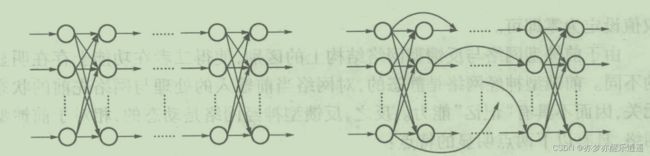
虽说没有回路,但是信息跨层传输也是OK的,如右图。大名鼎鼎的ResNet就是采取跨层传递的思路实现的。
反馈神经网络
因为回路的存在,反馈神经网络可以表现出时间特性,动态特性。
右图中任意两个神经元都有连接,这是比全连接更狠的全互联。左图就比较一般,更加常用点。
在反馈神经网络中,X输入不一定是必须的,因为内部回路的输出可以当做输入。
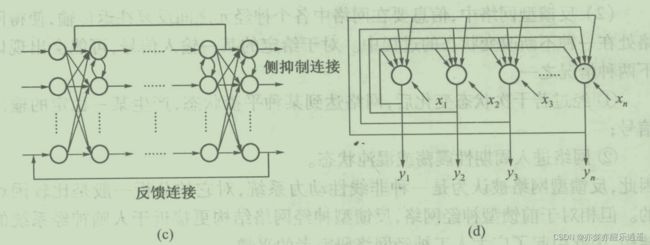
反馈型网络和前馈型网络的具体区别如下:
- 反馈网络的输入由当前输入与之前的输出有关,所以具有记忆性(此处感觉和RNN很像,但是我不确定RNN的网络结构是否有回路)
- 自己的输出影响输入,这种结构让反馈网络成为一种非线性动力系统,给定一个输入,基本是两个结果:
- 迭代到平衡
- 迭代到混沌或者周期态
虽然反馈型网络很复杂,但是更接近人脑网络,实际上,有学者就认为,人的记忆和脑回路有巨大关系。
人工神经网络的学习方式
学习方式大概分为:
- 权值学习。自动调整权值,现在主流方法
- 结构学习。自动调整结构,比较困难,但是可能是未来的突破口
不同的思想大概有四种:
- Hebb学习
- 误差修正型学习
- 竞争性学习
- 随机性学习
赫布(Hebb)学习
生物神经系统中存在自组织机制。
Hebb给出猜想:如果两个神经元同时处于兴奋状态(最好是前一个先兴奋,后一个紧接着兴奋),这说明两个神经元之间具有紧密联系,那么就应该加大连接强度,即权重。
w w w是权重, η \eta η是学习率,x是神经元的输出。如果输出同时为正或者同时为负,乘积就是正的,就会加强连接。
Hebb学习规则影响力还是比较大的,但是一些神经生理学的研究表明,Hebb学习对突触变化规律表达的还是不够准确,一方面没有赫布突触特性的直接证据,另一方面,赫布学习无法解释反复刺激之下的麻木情况(按照赫布理论,应该是越刺激越敏感)。
所以赫布规则需要进一步发展。
误差修正型学习
平常的神经网络(以及下面的多层感知机)就是这种训练方式,不多赘述。
竞争型学习
一种无监督学习方法,自组织特征映射网是竞争型网络的代表。
只需要给输入作为训练集,网络会自行组织训练数据,分类。
具体流程为,给定某个刺激模式,令一组神经元相互竞争(加强自己,抑制其他),选出输出最大的那一组神经元,加强其对刺激的响应能力(权重)。
不同的模式对应不同组的神经元,这就可以对数据进行分类了。
随机性学习
典型是玻尔兹曼机。
随机性学习很像模拟退火。网络变量(比如权重或者结构)随机变化,至于变化的好坏,由网络能量函数评估。一种简单的评估方法就是计算期望输出与当前输出的差距。
对于结果,有好也有坏,对于好的,直接接受,对于坏的,也应该有一定概率接受。因为如果一味地接受好的,可能陷入局部最优解情况(但是实际上对于超高维向量来说,几乎不可能陷入局部最优解情况)
多层感知机(误差修正型学习)
MLP,Multi-layer perception
感知机阶段
感知机我不打算细说,默认读者已经学过神经网络。
神经网络基础
最开始的感知机没有非线性激活函数,即,输入与输出是线性变换(仿射变换)关系,所以能解决的问题很有限,问题必须是线性可分的,比如实现与运算。
所以这个缺陷被发现了,有人写了本书《Perception》,指出感知机只能解决有限的问题,而XOR(异或)这种简单的问题可能都解决不了。


后面有人提出了多层感知机,解决了异或问题。其第一层与第二层之间采用阈值函数(非线性)。

此后,虽然有人证明了任何连续映射可以由一个三层前馈神经网络精确实现,但是人们仍然不能对多层感知机进行有效利用,研究陷入低谷。
BP网络阶段
时隔20多年,到了1986年,终于有人给出了BP算法,这是神经网络的里程碑。
其实之前就有人写了,只不过被忽略了,直到BP出现在了《Nature》上。
前面解决XOR问题的双层网络,用了阈值函数作为激活函数,这只是个巧合,到了BP阶段,终于有人意识到加深神经网络的关键:
通过在层之间加非线性激活函数,就可以不断提高网络对复杂函数的拟合能力。如果不加激活函数,再多层神经网络也只会是一个线性变换。
到这里,神经网络又一次进入高峰
自适应线性神经元网络
有人提出了这种网络,实际上这种网络没什么亮点,亮点在于损失函数用了LMS(Least Mean Square)最小均方误差。
现在这个也有很多人用。
径向基函数网络
因为迭代实际上就是函数逼近,而这又和插值有联系,所以这个网络是采用径向基函数实现这种联系。
具体我也懒得看了,我个人认为这项研究数学成分太大,我觉得重点应该放在网络架构和学习算法上,不需要用太精巧的数学方法。
霍普菲尔德网络与玻尔兹曼机(随机性学习)
霍普菲尔德网络是一个物理学家提出的,是一种动力系统,带有浓厚的传统工科色彩。这种网络通过让能量函数最小化来达成系统稳定态。但是这种容易出现局部最优现象,所以导入了概率,克服局部最优解,变成了玻尔兹曼机。
霍普菲尔德网络还和赫布学习有关系,所以在类脑研究中,会出现玻尔兹曼机之类的名词。
霍普菲尔德网络——网络结构
霍普菲尔德网络是全互联网络(前面说到过),用 I I I表示网络输入信号,w表示权重,s表示状态, ξ \xi ξ表示整合后的输出值。
霍普菲尔德网络中,神经元的输出和状态是一个概念。离散霍普菲尔德网络的状态就只有0/1或者-1/1。
以离散霍普菲尔德网络举例。
霍普菲尔德网络是一个动力系统。所谓动力系统,就是随着时间不断变化的系统。比如有一个霍普菲尔德网络,我给一个输入,这个网络就会不断变化,直到稳定(理论证明必然稳定)
也就是说,在输入与输出之间,不是马上就输出,而是是要经过一系列迭代变化的,在迭代过程中,权值不会发生变化,只是神经元的状态在不断更新,更新的原则就是加权和+阈值激活函数,以输出作为新的状态值:
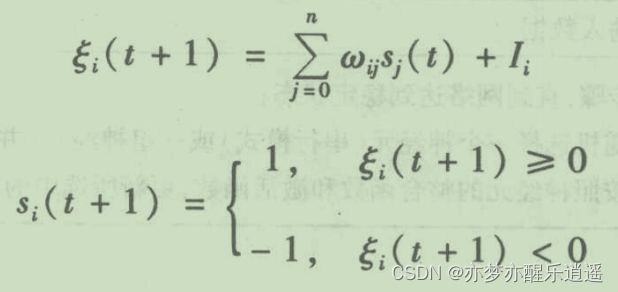
到这里还有很多没有解决的问题,比如权值w如何确定,如何更新,网络怎么训练。不过在此之前,先证明一下为什么系统一定会趋向于稳定:
能量函数简化后变成了这样。
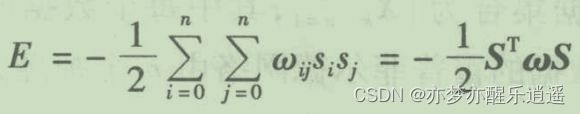
因为权重矩阵是下图形式,所以根据一个神奇的李雅普诺夫定理,就可以确定S的迭代是趋向于稳定的。也就是说,只要给定一个输入,网络必然会趋向于一个稳定的最终状态。
本节介绍了霍普菲尔德网络的结构,以及从输入到输出的过程,最后还补充了稳定输出的必然性证明。
联想记忆——训练算法
霍普菲尔德可以将一些类似的输入转换成相同的输出,这些输出统称为吸引子,因为其可以让附近的状态趋近于自己的状态。
这种机制从效果上说,有点像人类的联想记忆机制。即使是输入有残缺,也可以通过相似性,被吸引子吸引回原来的稳定状态。
在本章,我会讲一下霍普菲尔德网络的权值确定方法(仅用于联想记忆,其他任务的w可能不用这种方法确定)
在联想记忆网络中,假设你要记住k个样本,一个样本长为n。
那么权值就如下,可以看出,W是固定的:
在这个公式里,无论K如何变化,计算出的W矩阵的尺寸都是固定的,不信的可以试一试,所以网络理论上可以记住很多样本。
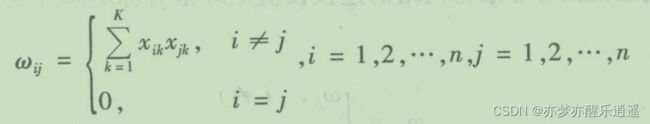
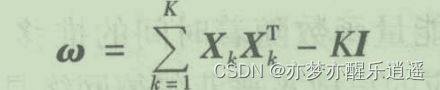
W是固定的,是用我们要记忆的样本计算出来的,所以W就隐含着这些样本的信息,对应k个吸引子。
当网络构建好后,只要输入和记忆的样本类似的样本,最终就会被吸引到记忆样本上去:
比如我们记住了第一行第一个图片,输入第一行第二个图片,网络就会开始迭代,迭代过程是第二行的三个图片,最终输出记忆中的样本。
除了残缺的样本,给一个噪声样本也可以实现回忆,比如第三行第一个图,输进去也可以被吸引到结果状态。
优化计算——解决最优化问题
经过理论证明,霍普菲尔德网络在迭代过程中,能量是递减的,那如果把能量当做目标函数,不就能实现我们平常最熟悉的最优化任务了吗?
以TSP(Travle Salse Problem)举例,说明霍普菲尔德网络如何实现最优化。
旅行商问题要求给出一个最佳路径,让人不重复地一次性走完所有节点,同时走的路程尽量短。
下图横轴代表城市,纵轴代表步数,维度均为n,所以该网络总的神经元个数为n×n。
i行j列为1代表第i步走到j城,为0代表不走j城。
最终的图像应该是,每一行只有一个是1,每一列也只有一个是1,从上到下按顺序拿出为1的节点,排列起来就是结果路径。
既然确定能量是必然减少的,那首先应该让某个能量和总路程正相关,如下式,实际上,E1就是总路程。
其中,s为状态,d为从一个城市到另一个城市的距离,这个式子的j从何而来我也不确定,姑且不细究了,直接当做总路程即可。
- 一行最多只有一个为1
- 一列最多只有一个为1所
- 有为1的节点总共有n个
这三个表述,综合起来就是:每行每列有且只有一个节点为1
那把这4个能量加权和形成一个新的能量E,当E最小的时候,也就意味着这些E1,E2,3,4都是最小的。
这里有一个E可以当做目标函数了,但是这个E不是构建霍普菲尔德网络的标准格式,所以要转换一下:
这个式子里多出了w和I,w是可以根据城市间举例矩阵和能量权重计算出来的。而I也是可以计算的。所以,根据问题给出数值的不同,E的形式和数值会有所不同。

构建好霍普菲尔德网络(E和W)后,求解问题就很简单了,随机喂进去一个I,然后迭代输出一个结果,取出为1的节点顺序排列后,就是比较优秀的解。
总结,在优化问题中,关键在于构建E函数,然后转化为霍普菲尔德网络标准能量函数+权重。
最后吐槽一下,霍普菲尔德的W是固定的,我个人感觉这是一个死物,不具备进化的能力,更像是一种初始化。
玻尔兹曼机
[Hinton G E. Boltzmann machine[J]. Scholarpedia, 2007, 2(5): 1668.]
没想到玻尔兹曼机也是大名鼎鼎的Hinton提出的。
霍普菲尔德网络的E一定会减少,这并不是一个好现象,因为这意味着这是一种贪心。既然是贪心,那就有可能陷入局部最优状态,所以引入了类似于模拟退火的概率机制,以一定概率接受较差结果。
具体引入模拟退火机制的地方,是激活函数。
以前的激活函数,根据 ξ \xi ξ的值,就可以确定结果是+1还是-1,但是现在的状态不再是确定的,而是概率。越大的 ξ \xi ξ,对应越大的+1概率。同时引入T温度常数,随着T逐渐减少,网络的迭代从随机过程变成了贪心过程。
具体分析,刚开始T很大,限制了 ξ \xi ξ的发挥,让+1的概率没有那么大,随着T不断降低,该过程回归到了霍普菲尔德网络。这和模拟退火几乎是一模一样的。
自组织特征映射网(竞争型学习)
灵感来源
以上的各种学习方式都属于监督学习,这个自组织特征映射网则是非监督学习方法。
无监督学习方法其实就是分类,每一个类别都可用少量的点来表达特征,这些点就叫做范型或者中心点。传统的无监督学习方法有矢量量化和聚类技术。自组织特征映射网兼顾了这两个技术,同时引入了降维的能力。
自组织特征映射网灵感来源于大脑皮层。大脑皮层,既然是皮层,那其实就是一个二维的结构。实际上,大脑皮层不完全是二维的,因为每个单元都是柱状的(皮层柱 cotrical column),一个柱内有6层细胞,不过这6层相对于广大的面积就微不足道了,所以我们姑且认为大脑皮层是二维的。
大脑皮层是二维,但是我们平时输入的数据可不仅仅是二维的,可以说是高维的,而大脑皮层就实现高维数据到二维数据的转换。自组织特征映射网就是模拟了这个特征。
网络结构
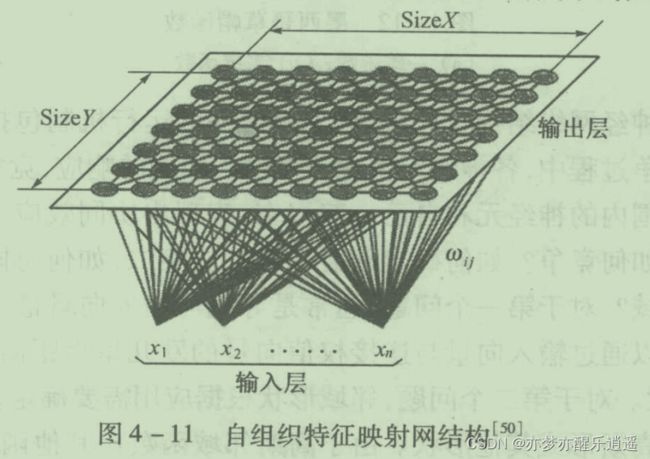
自组织特征映射网结构有两层,一层输入层,维度不限,一层输出层,逻辑上我们把这一层看做是二维的,节点之间具有相邻关系。
网中存在两种连接:
- 输入到输出的前向连接(这里用全连接),通过权值提取特征
- 输出层神经元之间的侧连接,用于影响特定距离范围输出层神经元的兴奋性
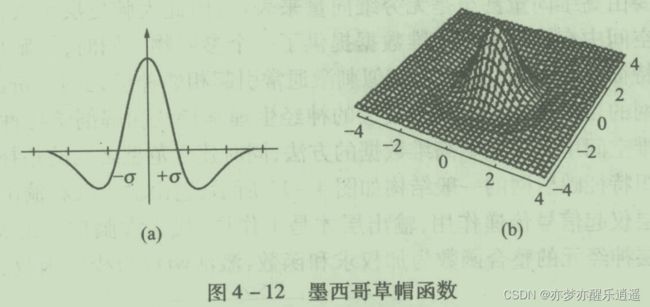
前向链接简单用全连接,而侧连接采用墨西哥草帽的方式连接:
- 最近的,协同区,激活
- 稍微远一些,侧抑制区,抑制
- 很远,弱激励区,微弱的激活
虽说是分三种,但是一般来说就只会注意协同区,所以又把协同区叫做激活气泡,其他的区域一概视为抑制区。
说到这里,其实你已经明白不需要显式地给出侧连接了,因为逻辑距离已经把节点之间的连接表示出来了。
训练方法
说完结构了,可以说一说如何训练了。两个过程:
- 竞争,从输入到输出的前向传播。
- 协同,在输出层的侧向传播。
先说竞争。
所谓竞争,就是通过一个x输入,来激活某一个获胜神经元。如何选择?找出与x最接近的权值对应的神经元即可。
有人听到这里就迷糊了,我们从维度来解释一下。因为是全连接,所以一个输出层神经元必然和n个输入层节点连接,所以一个输出神经元对应一个n维权重向量w,而给定的输入也是n维的x,所以这俩维度一样。我们需要遍历所有输出层神经元,找出 w i j w_{ij} wij与x最接近的神经元。
至于接近,可以用欧氏距离衡量。
再说协同。
协同的第一步是确定邻域,领域形状很多,但墨西哥草帽最常用。
此外,邻域还会随着时间逐渐收缩,从刚开始的全局,到最后的一个。
确定了邻域以后,就要对领域中的每一个神经元进行权值更新操作了,具体更新规则如下:
领域中的更新,领域外的不变。
注意,w是n维向量。理论上w应该是双下标,毕竟是二维的,但是估计是为了好编程,就写成了单下标,毕竟二维只是逻辑上的,实际就是个数组。
![]()
理解与总结
这么个调整过程宏观上有啥效果呢?
对于一类x1,每次激活,都会调整该区域神经元对x1的响应权重,从公式来看,是让w1趋近于x1,那下一次再来个x1,就更容易响应了(因为w1和x1的欧氏距离更小了)。
但是对于另一类x2,只要和x1有一定差距,就永远不会被w1响应。虽然不会被w1响应,但是总有属于x2的w2响应他啊,那w2就会越来越趋近于x2,x2也就不需要理会w1了。
就这样,随着训练,不同区域的神经元都会将其权重调节,对应不同类别的x。那最后不同类别的x就会通过不同区域的w,激活不同区域的神经元。把区域分类,就可以实现聚类,同时把高维数据降维到二维。
这里给出训练流程,对照上面的描述,回顾一下。
这个网络总的来说,就是把高维的分类变量降维到二维的节点群,这就是一种映射。而所谓的自组织,就是指w的自动调节。
网络有如下特性:
- 拓扑排序特性。在映射过程中,空间关系保持不变,在高维空间中相近的数据,映射到二维空间也会在同一个区域中。
- 密度匹配特性。在映射过程中,类别的密度保持不变,在高维空间中分布比较密集,区域比较小的数据,映射到二维空间对应的神经元区域也比较小。
- 输入空间逼近特性。维度的转换其实是一种近似的表达,实现了数据压缩(指聚类,用一类代表无限的数据)和维度压缩(二维代替n维)
- 特征选择特性。看不懂。

机器学习
学习没有明确的定义,目前也不应该被他人的理念拘束。
简单来说,学习的核心就是知识积累,知识提炼,在下一次行动中有更好的表现。下图给出常见的学习体系,不过仅供参考,毕竟大脑中真实的学习是否如此并不确定,不要拘泥于别人的想法。
主要策略
大致上,有机械式学习,指导式学习,类比学习,归纳学习,解释学习,这些学习理论上都是有用的,只是人们不见得能利用好这些规律。发现与利用这些规律的就是科研的意义。
机械式学习
将知识直接记忆,碰到问题就搜索X,如果以前见过一样的X,就输出一个对应的Y。就好比一个只会背答案的学生一样。
当然,机械式学习系统也不一定只有记忆,也会搭配一些计算,每次来了新的X,系统会评估一下,是计算Y速度快还是搜索Y速度快,哪个快就用哪个。总的来说,机械式学习要关注三个点:
- 储存结构。随着记忆的知识越来越多,即使你用二分法排列X,你的搜索效率也不会很大。而人脑,即使是死记硬背,搜索到对应X的速度也是很快的,而且具有一定的模糊搜索能力,可见人脑在大量数据的搜索能力上,是强过电脑的。
- 环境稳定性。机械式学习的X是固定的,精确的,稍微有一点变化就搜不到了,如果环境变化太剧烈,只是体系就无法适应了。相比之下,人脑的模糊搜索能力对环境的适应性是很强的
- 记忆与计算的平衡。前面说了,搜索和计算,谁比谁快还不一定呢,所以要用算法评估这两个哪个快,如果这个知识你储存以后,下次搜索的速度会很慢,那还不如不记忆,下次重新计算就是了。另一种就是,很久没用的老内容可以删掉,减少了知识量也就可以维持一定的搜索速度了。
这里给出一个记忆与计算结合的智能系统:A.L.Samuel的西洋跳棋
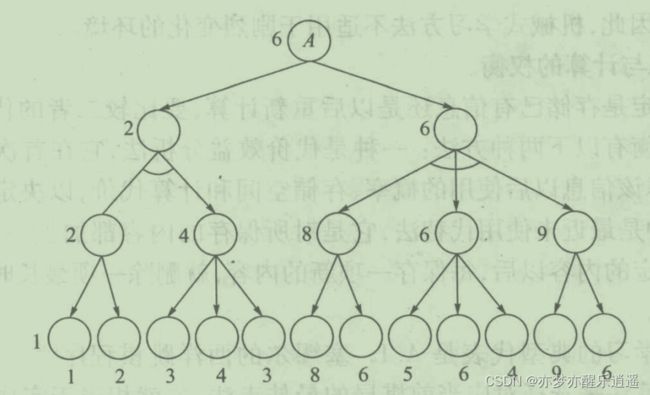
西洋跳棋采用博弈树搜索,步长为3。下面第一个图,根节点为A,计算可得A的倒推值为6。假设经过评估,系统决定把A记忆下来。当以后走到A节点的时候,就不需要重新计算了,直接用记忆好的倒推值即可。
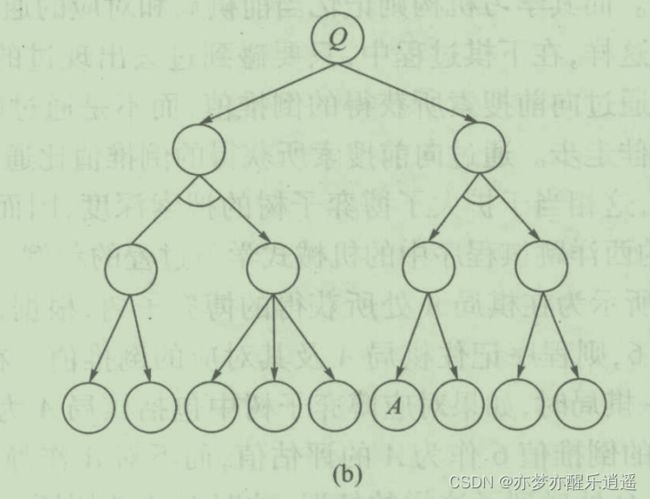
下图给出了另一盘棋局,前面已经记忆了A节点,假设图中像A节点一样,已经把最下层的节点都记忆过了,那么从Q节点就可以通过三步搜索得到6步搜索的效果。因为到最底层节点就不需要再搜索三层了,直接调取记忆即可。
宏观上来说,记忆加快了推导的速度,让我们用3层的时间实现了6层的效果,代价就是要花费空间记忆。就像我们平时做题,也是记忆+推导配合的,记住了现成的定理,而我们用定理去推导计算。
IDEA:
其实机械式学习也不是一无是处,人在学习的时候,其实并不完全是归纳概括,在最开始就是死记硬背,但是在后面不断的行动中不断整合,加深理解,形成了自己的逻辑。那可以用机械式学习做一个缓冲,新来的知识如果能快速理解那最好,不能就先记着,然后拉长时间线不断地去思考(我本人就是这么干的)
还有就是,在进行一个回合决策的时候,可以计算和记忆一起上,能用记忆就用记忆,用不了记忆就计算,就像我们平时做题,也是记忆+推导配合的,记住了现成的定理,而我们用定理去推导计算。事后还要对这一回合进行总结,对记忆中没有的东西进行提炼,提升下一次的表现,就好比我们虽然可以用背答案的方式做题,但是还是希望能有自己的想法,亲手做出一道题。
指导式学习
指导式学习,在下图的前提下,又增加了指导者角色。就好比我们可以通过做题,实践学习,但是也可以通过老师直接传授知识来学习。这种过程,本质上来说就是把老师说的话经过自己的加工后再记忆。
具体流程有5步:
- 请求,即智能体向指导者请求教导(但是我感觉更像是指导者教导智能体,注意主次的关系)。分为简单请求,复杂请求,也可以分成被动请求,主动请求。
简单请求,即老师说什么,我就学什么,老师给出一个一般性的结论,我经过加工,得到一个适合我的具体结论。复杂请求,在简单请求的基础上,还要求指导者根据智能体知识库的情况,给出修改意见。这就好比学生基于老师的教导,简单加工后根据自己已经掌握的知识再次追问老师,老师就可以更加针对性地给出建议。
被动请求,老师说什么我就学什么,不做反馈。主动请求,智能体还可以主动问老师问题,让老师的教导注意力集中在一定范围内,更有针对性。 - 解释,智能体将老师的教导加工成便于自己理解的知识。比如机器比较喜欢精准,无二义性的东西,但是教导者的自然语言比较模糊,从自然语言转到机器语言就是解释。当然,你也可以限制指导者的语言,但是者不利于提高系统的适应性(你不行别怪老师不行)
- 实用化,把解释后的知识转换成具体的知识。解释只是让智能体听懂指导者的语言,但是还没有理解加工,实用化就是把老师给出的一般性的结论细化成自己的结论。可以说,解释是实用化前的预处理。
- 归并,把新的结论加入知识库。老师的教导转化成你自己的结论后,就要记忆,储存。此时会出现两个问题:重叠使用问题,结论冲突问题。重叠使用问题就是你新学到的知识比之前的某条知识更具有一般性,那要么就把以前的知识抛弃了,用这条更好的,要么就把这条细化了。结论冲突问题就是相同的前提,不同的结论,很明显有一条知识是错的,这就需要排除错结论。
- 评价,新知识好不好。结论可对可错,对系统有可能有坏处。一种是直接让系统去在实际问题上测试,如果表现更好,那就是好,不好就说明那条知识没加对。另一种方法是预测,通过算法去评估。
指导式学习也是有用的,符合平时我们在学校的部分学习场景。
类比学习
类比学习就是通过场景的相似性,甚至是场景在本质上的相似性,来讲经验迁移的学习。
所谓场景的相似性,就是你在做两道很像的题的时候,你可以做出微小的适应。而有的场景虽然看起来不一样,但是在本质上是相似的,这也能迁移,比如你可以从一个小群体中的利益争斗,推广到社会集体,国际上的利益争斗,这就是所谓的“道”。但是这个对机器来说难度还太高,人类中能参悟大道的尚且少之又少,机器又怎么能做到?
不过,因为类比学习太重要了,所以机器学习中很多人都在研究类比学习,类比推理。详见后文。
解释学习
解释学习着眼于如何将知识分析,分解。在已有的领域知识支持下,通过对单个例子的分析,抽取出解决问题的因果链条,获得控制性知识。
貌似因果学习就是搞这个的,但是看起来着实不太好做,毕竟人做到这个都不容易,目前应该只是在探索基本的因果学习。详见后文。
归纳学习
归纳学习有点像因果学习,都是从局部推广,但是因果学习是直接推导出链条,而归纳学习更多的是对规律的发现,挖掘,就比如现在的深度学习,更多的是拟合,而不是发现内在逻辑。
总的来说,归纳学习可以分成监督学习,非监督学习,以及强化学习。
监督学习的输入是(X,Label),每一个X都有一个期望的值。监督学习的效果往往很好,但是人类平时也有很多学习不需要监督,而且监督学习需要人去标注样本,工作量比较大。
非监督学习不需要你有具体的期望,智能体对样本进行分类,分类过程就是在发现样本内部的规律,差异。
强化学习介于监督学习和非监督学习之间,输入也是样本+标签(比如state,action),但是标签是在探索环境的过程中产生的(reward)。通过大量的探索,相当于自动生成了大量的样本+标签。
本文后面会简要介绍几种机器学习方法:
监督学习有:规则集的归纳学习,决策树学习,贝叶斯学习。
规则集的归纳学习和决策树学习都是类似于IF-ELSE的分支结构,只不过规则集是直接学一阶逻辑,而决策树是先获得分类树,再转换成一阶逻辑。贝叶斯学习是基于贝叶斯规则的统计学习方法,其中关键问题是进行条件概率分类。具体的贝叶斯学习有朴素贝叶斯分类器与贝叶斯信念网,两者都可以说是条件概率分类的简化版本。
非监督学习其实就是聚类,主要有划分聚类和层次聚类。
其实前面讲的神经网络也可以划分为监督学习和非监督学习两种,感知器,BP之类的误差修正模型都是监督学习,霍普菲尔德网络也有一些监督特性。而自组织特征映射网这种竞争性学习,是典型的非监督学习,而自组织特征映射网本身的目的就是聚类。脉冲神经网络领域也有一些非监督学习。
类比学习方法
类比学习的核心就是相似性,但是,比较那一个层面的相似性,如何比较相似性,是区分不同类比学习的重点。
属性类比学习
TODO
转换类比学习
TODO
基于解释的学习
TODO
规则集的归纳学习
TODO
决策树学习
决策树可以看做if-then的分支结构,针对离散数据(连续数据需要进行分割离散化)
决策树
决策树如下图,比较直观。其中,非叶节点代表属性,叶节点代表决策结果,一条路径就代表一个决策过程(规则)。
决策树构建(ID3算法)
如何通过输入的问题构建决策树?
宏观思路
下面的算法描述比较刻板,其实就是一个递归。首先明白,Example就是训练数据,Attributes是属性,有很多项,而Targets是结果,只有一项(假设两类):
- 如果Target全部一样,那说明不用分割了,递归结束,直接返回单节点树
- 如果Target不完全一样,但是没有可用的属性了,没法分类,那就给他划归到最大的类别里就行,类似于默认了
- 1和2都不符合,也就是正常情况,这才会进行分割。
- 从若干属性里选出最好的属性。就是让整体的分支尽可能少,深度尽可能浅。更加直观的说,就是用一个属性就可以将一个分类干掉。比如满足某一个属性后,直接就能决定一个分类,那肯定要先把这一个类排除出去更有利于后面的分类。具体会用信息熵计算。
- 把根节点设为这个属性,而且以后更深层的分类就不需要用这项属性了
- 从根节点延伸分支,每一个分支对应这个属性的一个类别,如果这个类别里有Example,就用用这些Example+去除这一项属性作为参数,递归调用ID3算法(其实就是让这个子集再一次分类)。如果这个类别里没Example了,那就没办法继续分类训练了,就默认认为这一个分支属于最大的类别了。
信息熵与属性选择
上面的算法其实比较朴素,就是不能分支就结束,能分支就继续递归分支。关键在于,如何选出最好的属性?
首先给出样本整体信息熵的定义。相比于交叉熵,信息熵是概率向量内部的计算。
拿分类来举例,P是一个类别的概率,总和为1。如果所有P都相等,熵是最大的(因为你完全不能通过概率确定你的结果),如果有一个P=1,其他P=0,那熵就是0(结果就是那个P=1对应的类别)。
如果使用一个Attribute将数据集分割,分割后的熵如何计算?加权就好了。
那分类前-分类后,是不是就是熵减少的值,熵减少的越多,类别就越有序,代表对信息增益的越多,决策目标就越清晰。
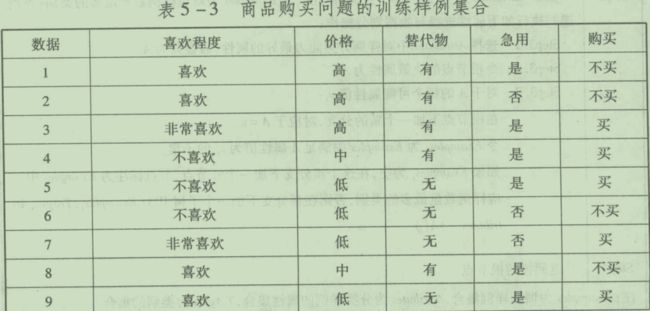
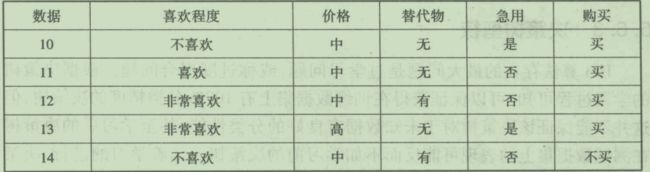
例子
首先计算S的整体熵。5个不买,9个买。
之后遍历所有Attribute项,分别计算Entropy(S,A),对于急用属性,计算如下:
有8个急用,6个不急用。对于急用的8个,与6个不急用,在各自的内部计算整体Entropy,然后加权。
遍历完后,就可以计算出所有Attribute的信息增益
选择最大信息增益,所以就用喜欢程度作为当前的分类节点。喜欢程度有3类,所以产生3个分支,对于每个分支,检查一些特殊情况:
- 非常喜欢里,类别一致,对应Step2,成为叶节点。
- 另外两个子集类别不一致,继续递归调用,直到类别单一(归为对应类叶节点)或者没属性可分(归为默认叶节点)
- 有的属性没有用到,就已经把决策树分完,说明不是所有属性都要用到,就好像你自己做决定的时候,会忽略很多东西。
决策树剪枝
学到这里,你就可以明白,决策树对于训练集的利用率是100%的,所以完整跑下来,训练准确率一定是100%,很容易就会过拟合,导致测试集效果差很多,面对未知数据更是不堪。
减小过拟合的方法就是剪枝:
- 预先剪枝。在决策树生长过程中选择性停止生长
- 后剪枝。生成决策树后剪枝
剪枝需要的评估依据为最小描述长度(bit位)=决策树编码长度+例外情况编码长度
具体计算暂且略过,TODO。
总的来说,就是用这个最小描述长度替代信息增益,来决定决策树生长的方向,使得每次扩展决策树后,最小描述长度增长量最小(预先剪枝)。待生成一颗完整的决策树以后,自下而上剪枝,直到不能减少最小描述长度为止(后剪枝)。