机器学习 多变量线性回归

一、前言

前面一系列文章介绍了单变量线性回归：
机器学习 单变量线性回归 (1)背景介绍
梯度下降法解单元函数
向量微积分——理解梯度
机器学习 单变量线性回归 (2)梯度下降法
机器学习 单变量线性回归 (3)代码实现

通过上述方法，我们可以通过房子面积$x$、简单地预测房价$y$。但实际情况是，房价不仅仅是由面积决定，还有房间数、楼层、朝向等一系列因素变量决定。那么怎么解决呢？

二、特征描述

现在影响房价的特征因素有很多（房间数、楼层、朝向等），我们使用$(x_1,x_2,...,x_n)$表示。

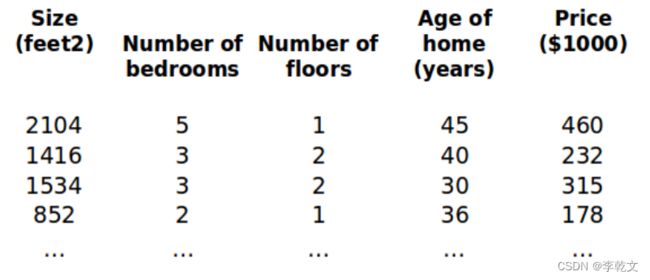
变量约定如下：
代表训练集中实例的数量
n 代表特征的数量
$x$是包括所有实例特征向量的矩阵，为了方便计算，一列为一个实例，m个实例有m列：
$x=\left[\begin{array}{cccc}{x}_1^{(1)}& x_1^{(2)}& ...& x_1^{(m)}\\ x_2^{(1)}& x_2^{(2)}& ...& x_2^{(m)}\\ ⋮& ⋮& ...& ⋮\\ x_n^{(1)}& x_n^{(2)}& ...& x_n^{(m)}\end{array}\right]$
$(x^{(i)},y^{(i)})$代表训练集中第 个实例
比方说，上图的
$x^{(2)}=\left[\begin{array}{c}1416\\ 3\\ 2\\ 40\end{array}\right]$
$x_j^{(i)}$代表特征矩阵中第 个实例的第 个特征，如上图的$x_2^{(2)}=3,x_3^{(2)}=2$

三、假设函数

$x^{(i)}$表示第$i$个实例，支持多变量的假设函数 ℎ 表示为：$$h(x^{(i)})=w_0+w_1{x}_1^{(i)}+w_2{x}_2^{(i)}+...+w_n{x}_n^{(i)}$$

为了便于后续的矩阵运算，我们引入$x_0^{(i)}=1$，则

设 $w=\left[\begin{array}{ccccc}{w}_0& w_1& w_2& \dots & w_n\end{array}\right]$，$x^{(i)}=\left[\begin{array}{c}{x}_0^{(i)}\\ x_1^{(i)}\\ x_2^{(i)}\\ ⋮\\ x_n^{(i)}\end{array}\right]$，那么$$h(x^{(i)})=w{x}^{(i)}=w_0{x}_0^{(i)}+w_1{x}_1^{(i)}+w_2{x}_2^{(i)}+\cdots +w_n{x}_n^{(i)}$$

注意：为了方便计算，与网上大部分资料的$h(x^{(i)})=w^T{x}^{(i)}$有点不同，我们直接设$w$为1行n列的矩阵，而不是n行1列。
还有一点要注意的是，大部分数据集的$x$是一行一个实例，与这里的一列一个实例不同，训练样本前需要注意转置。

矩阵向量乘法：
$\left[\begin{array}{ccc}1& 2& 3\end{array}\right]\ast \left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]=\left[\begin{array}{c}1\ast 1+2\ast 2+3\ast 3\end{array}\right]=14$
$\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]\ast \left[\begin{array}{ccc}1& 2& 3\end{array}\right]=\left[\begin{array}{ccc}1\ast 1& 1\ast 2& 1\ast 3\\ 2\ast 1& 2\ast 2& 2\ast 3\\ 3\ast 1& 3\ast 2& 3\ast 3\end{array}\right]=\left[\begin{array}{ccc}1& 2& 3\\ 2& 4& 6\\ 3& 6& 9\end{array}\right]$

四、代价函数

通过《机器学习 单变量线性回归 (1)背景介绍》可以知道，代价函数表示为
$$\begin{array}{rl}J(w_0,w_1,\dots ,w_n)& =\sum _{i=1}^m[h(x^{(i)})-y^{(i)}{]}^2\\ & =[w_0{x}_0^{(1)}+w_1{x}_1^{(1)}+\cdots +w_n{x}_n^{(1)}-y^{(1)}{]}^2+[w_0{x}_0^{(2)}+w_1{x}_1^{(2)}+\cdots +w_n{x}_n^{(2)}-y^{(2)}{]}^2+\cdots +[w_0{x}_0^{(m)}+w_1{x}_1^{(m)}+...+w_n{x}_n^{(m)}-y^{(m)}{]}^2\end{array}$$
同样为了方便后面的计算，我们用$J=\frac{1}{2m}{\sum }_{i=1}^m[h(x^{(i)})-y^{(i)}{]}^2$来表示代价函数。
在多特征变量时，$x^{(i)}$是一个包含多个特征数值的向量。

五、梯度下降

对$J(w)$中的$w_0,w_1,\dots ,w_n$分别求偏导，求导相关知识可参考《导数与偏导》。
重复以下计算：
$\begin{array}{rl}{w}_0& =w_0-\eta \ast \frac{\partial }{\partial w_0}J(w)\\ & =w_0-\eta \ast \frac{\partial }{\partial w_0}\frac{1}{2m}\sum _{i=1}^m[w_0{x}_0^{(i)}+w_1{x}_1^{(i)}+\cdots +w_n{x}_n^{(i)}-y^{(i)}{]}^2\\ & =w_0-\eta \ast \frac{1}{m}\sum _{i=1}^m[w_0{x}_0^{(i)}+w_1{x}_1^{(i)}+\cdots +w_n{x}_n^{(i)}-y^{(i)}]x_0^{(i)}\\ & =w_0-\eta \ast \frac{1}{m}\sum _{i=1}^m[h(x^{(i)})-y^{(i)}]x_0^{(i)}\end{array}$

$\begin{array}{rl}{w}_1& =w_1-\eta \ast \frac{\partial }{\partial w_1}J(w)\\ & =w_1-\eta \ast \frac{\partial }{\partial w_1}\frac{1}{2m}\sum _{i=1}^m[w_0{x}_0^{(i)}+w_1{x}_1^{(i)}+\cdots +w_n{x}_n^{(i)}-y^{(i)}{]}^2\\ & =w_1-\eta \ast \frac{1}{m}\sum _{i=1}^m[w_0{x}_0^{(i)}+w_1{x}_1^{(i)}+\cdots +w_n{x}_n^{(i)}-y^{(i)}]x_1^{(i)}\\ & =w_0-\eta \ast \frac{1}{m}\sum _{i=1}^m[h(x^{(i)})-y^{(i)}]x_1^{(i)}\end{array}$

$⋮$

$\begin{array}{rl}{w}_n& =w_n-\eta \ast \frac{\partial }{\partial w_n}J(w)\\ & =w_n-\eta \ast \frac{\partial }{\partial w_n}\frac{1}{2m}\sum _{i=1}^m[w_0{x}_0^{(i)}+w_1{x}_1^{(i)}+\cdots +w_n{x}_n^{(i)}-y^{(i)}{]}^2\\ & =w_n-\eta \ast \frac{1}{m}\sum _{i=1}^m[w_0{x}_0^{(i)}+w_1{x}_1^{(i)}+\cdots +w_n{x}_n^{(i)}-y^{(i)}]x_n^{(i)}\\ & =w_0-\eta \ast \frac{1}{m}\sum _{i=1}^m[h(x^{(i)})-y^{(i)}]x_n^{(i)}\end{array}$

$\eta$称之为学习率，控制梯度下降时每一段走的距离。
一直迭代计算，直到$w_0,w_1,\dots ,w_n$变化很小为止，代表已经达到最小值或者局部最小值了，此时$w$确定下来。

最终批量梯度下降的矩阵运算写法是$w=w-\frac{\eta }{m}(wx-y)x^T$，代码实现时可以返回来查看这个公式。下面我们来推导一下矩阵运算公式。

在本文，包括后续的逻辑回归文章中：

$w=\left[\begin{array}{ccccc}{w}_0& w_1& w_2& \dots & w_n\end{array}\right]$，是1行、n+1列的矩阵

加入前置$x_0$的特征矩阵$x$，是n+1行、m列的矩阵：
$x=\left[\begin{array}{cccc}{x}_0^{(1)}& x_0^{(2)}& ...& x_0^{(m)}\\ x_1^{(1)}& x_1^{(2)}& ...& x_1^{(m)}\\ x_2^{(1)}& x_2^{(2)}& ...& x_2^{(m)}\\ ⋮& ⋮& ...& ⋮\\ x_n^{(1)}& x_n^{(2)}& ...& x_n^{(m)}\end{array}\right]$

$x^T=\left[\begin{array}{ccccc}{x}_0^{(1)}& x_1^{(1)}& x_2^{(1)}& ...& x_n^{(1)}\\ x_0^{(2)}& x_1^{(2)}& x_2^{(2)}& ...& x_n^{(2)}\\ ...& ...& ...& ...& ...\\ x_0^{(m)}& x_1^{(m)}& x_2^{(m)}& ...& x_n^{(m)}\end{array}\right]$

$y$为数据集结果，是1行m列的矩阵：
$y=\left[\begin{array}{cccc}{y}^{(1)}& y^{(2)}& \dots & y^{(m)}\end{array}\right]$

小提示：若A、B两个矩阵可以相乘，则结果的行数为A的行数，列数为B的列数

$wx=\left[\begin{array}{ccccc}h(x^{(1)})& h(x^{(2)})& \dots & & h(x^{(m)})\end{array}\right]$，表示m个实例的预测值，($w$ 有1行，$x$有m列，结果是1行m列)

$wx-y=\left[\begin{array}{cccc}h(x^{(1)})-y^{(1)}& h(x^{(2)})-y^{(2)}& \dots & h(x^{(m)})-y^{(m)}\end{array}\right]$

$(wx-y)x^T=\left[\begin{array}{cccc}{\sum }_{i=1}^m[h(x^{(i)})-y^{(i)}]x_0^{(i)}& {\sum }_{i=1}^m[h(x^{(i)})-y^{(i)}]x_1^{(i)}& \dots & {\sum }_{i=1}^m[h(x^{(i)})-y^{(i)}]x_n^{(i)}\end{array}\right]$
结果是1行n+1列，正好等于w矩阵的维度。引入学习率以及m，就得到公式$w=w-\frac{\eta }{m}(wx-y)x^T$

六、原生代码实现

生成40组有5个特征变量的模拟数据，并将其拆分为训练数据和验证数据。我们在训练模型的时候使用训练数据，训练好后用验证数据验证模型效果。

from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np

#生成模拟数据
X,Y=make_regression(n_samples=40, n_features=5,n_targets=1,noise=1.5,random_state=1)

#添加前置 x0=1
temp = np.ones([X.shape[0],X.shape[1]+1])
temp[:,1:] = X #第[0]行到最后一行的(第[1]列到最后一列)赋值为X
X = temp

# 将数据分割为训练和验证数据，都有特征和预测目标值
# 分割基于随机数生成器。为random_state参数提供一个数值可以保证每次得到相同的分割
train_X, val_X, train_y, val_y = train_test_split(X, Y, random_state = 0)
print(train_X.shape, val_X.shape, train_y.shape, val_y.shape)

运行结果可以看到30组用于训练，10组用于验证：

(30, 6) (10, 6) (30,) (10,)

训练模型，此处用到了矩阵的dot运算，批量对$w_0,w_1,\dots ,w_n$进行梯度更新，将其展开即是第五节中的梯度下降公式：

#损失函数
def loss(preY,trainY):
    return ((preY-trainY)**2).sum()/(2*m)

learn_rate=0.5 #学习率
m=train_X.shape[0]
n=train_X.shape[1] #由于添加了前置，这里的n等于文章中的n+1

w=np.zeros([1,n]) #初始化参数w，1行n列
# train_y=train_y.reshape([1,m])

count=0 #迭代次数

#迭代
for i in range(1000):
    count+=1

    preY=w.dot(train_X.T) #预测值，1行m列，由于数据集是m行n列，这里的train_X.T就是文章中的x

    w_C=(learn_rate/m)*(preY-train_y).dot(train_X)
    if count%10==0:
        #每迭代10次则输出误差值
        print('epoch:',count,'loss:',loss(preY,train_y))

    #若w变化不大，则暂停迭代，模型训练完成
    if (np.abs(w_C)<0.001).all():
        print(w_C)
        break

    w-=w_C

print(count,w)

运行效果：

epoch: 10 loss: 38.342743157775985
epoch: 20 loss: 4.604601047469489
epoch: 30 loss: 1.2497710697935083
epoch: 40 loss: 0.7707107129364879
epoch: 50 loss: 0.700164695596168
epoch: 60 loss: 0.6897533892651387
epoch: 70 loss: 0.688216635124676
epoch: 80 loss: 0.6879898011002854
[[ 0.00065135 -0.00056317  0.00010236 -0.00058119 -0.00093601  0.00022956]]
83 [[-0.18016153 32.3837453  86.79018232 45.36247886 38.46956237 67.18053038]]

迭代了83次，最后确定了$w$。

验证模型效果：

print(w.dot(val_X.T))#由于数据集是m行n列，这里的val_X.T就是文章中的x
for i in range(val_X.shape[0]):
    x=np.array(val_X[i])
    print(f'预测值:{w.dot(x.T)}  \t实际值:{val_y[i]}  \t误差:{w.dot(x.T)-val_y[i]}')

运行效果：

[[  64.53517884   70.12258273   92.63818859 -189.68663318  -63.66320335
   -36.38921406   75.9091532   133.12284219  -90.22772668   59.38660621]]
预测值:[64.53517884]  	实际值:65.80873452422097  	误差:[-1.27355569]
预测值:[70.12258273]  	实际值:67.38192779493849  	误差:[2.74065494]
预测值:[92.63818859]  	实际值:91.73158736991597  	误差:[0.90660122]
预测值:[-189.68663318]  	实际值:-191.18391678049176  	误差:[1.4972836]
预测值:[-63.66320335]  	实际值:-62.01267481049975  	误差:[-1.65052854]
预测值:[-36.38921406]  	实际值:-33.58486580135441  	误差:[-2.80434826]
预测值:[75.9091532]  	实际值:72.87828417172948  	误差:[3.03086902]
预测值:[133.12284219]  	实际值:130.07435549898284  	误差:[3.04848669]
预测值:[-90.22772668]  	实际值:-90.94287343001048  	误差:[0.71514675]
预测值:[59.38660621]  	实际值:59.96376003207172  	误差:[-0.57715382]

七、sklearn代码实现

from sklearn.linear_model import LinearRegression
import joblib

#初始化模型
lr_model = LinearRegression()
#训练
lr_model.fit(train_X, train_y)

#保持模型
joblib.dump(lr_model, './LinearRegression.model')

#加载模型，在实际应用中直接加载已训练好的模型
lr_model = joblib.load('./LinearRegression.model')
 
#预测
y_pred = lr_model.predict(val_X)

print("Prediction on test set:", y_pred)
print("Score on test set:", lr_model.score(val_X, val_y))

运行结果

Prediction on test set: [  64.52367709   70.11321556   92.6383027  -189.67902945  -63.6821749
  -36.39093426   75.88751915  133.11449579  -90.2272863    59.39794385]
Score on test set: 0.9995420735156715