概率论与数理统计学习：随机事件（一）——知识总结与C语言实现案例

大家好，我将用这个专题来记录我学习概率论与数理统计的过程，希望大家多多支持。

这一篇呢主要是了解一下随机事件的基本概念、事件的概念和古典概率模型。首先，我们先介绍随机事件的一些相关概念。

基本概念

试验：我们把对某种现象的一次观察、测量或进行一次科学实验，统称为一个试验。

随机试验：如果试验在相同的条件下可以重复进行，且每次试验的结果是事前不可预知的，则称此试验为随机试验，也简称为试验，记为$E$。

样本空间：称试验的所有可能结果组成的集合为样本空间，记为$\Omega$。

样本点：样本空间中的一个元素，也就是随机试验的单个结果。

说了这么多，是不是该举一个例子来说明一下上面的几个概念呀？那么就拿我们日常生活中最常见的扔骰子来说吧！
一般来说，掷一颗骰（tou）子，它的点数有6种可能，咳咳，上面的是个例外。那么每掷一次我们会观察它的点数，所以掷一次骰子可以称之为一次试验，而每次掷骰子的时候条件都相同，且结果不可预知，那么这一次试验也可以称之为随机试验，而掷一次骰子共有6种结果，把这6种结果放在一个集合里，那么这个集合就是它的样本空间，每一次掷骰子的结果也就是一个样本点。

那么继续我们的概念了解

随机事件：样本空间中的任意一个子集。简称事件。

基本事件：一个随机事件中只含一个样本点，就称为基本事件。

必然事件：由于样本空间$\Omega$包含了所有的样本点，且是$\Omega$自身的一个子集，每次试验它必定发生，所以称为必然事件。

不可能事件：空集$\varphi$不包含任何样本点，它也是样本空间的一个子集，且在每次试验中总不发生，所以称为不可能事件。

☁️ 事件的关系

因为事件是一个集合，因此有关事件的关系、运算等也按照集合的相关规则来处理。根据事件发生的含义，我们就可以给出事件的关系与运算的含义。那么什么是“事件发生”呢？

简单来说就是一次试验的结果在事件所包含的结果中。例如，将事件A表示我明天上课会迟到，如果我确实迟到了，那么事件A就发生了，如果美迟到，那么就没有发生。下面一一介绍。

假设$\Omega$是试验$E$的样本空间，进行一次试验。

$A\subset B$：若事件A发生，必有事件B发生。

对于这种情况，一般只考虑事件A就行了。

$A\cup B$：事件A与事件B的和。

对于这种情况，只要满足事件A或事件B有一个发生即可。

$A\cap B$或（$AB$）：事件A与事件B的积或交。

对于这种情况，必须要满足事件A和事件B同时发生才行。

$A-B$：事件A与事件B的差。

对于这种情况，假设事件$A=\{1,2,3\}$，事件$B=\{3,4,5\}$，$A-B=\{1,2\}$，也就是如果事件A中有样本点与事件B中的样本点相同，则将此样本点从A中删去。注意，事件A和事件B都含有空集。

$\Omega -A$与$A$：事件$\Omega -A$与事件$A$为对立事件，记为$\overline{A}$。

❗️ 重点：分清对立和互斥事件的概念。对立事件一定是互斥事件，而互斥事件不一定是对立事件。

☁️ 事件的运算

交换律：$A\cup B=B\cup A$，$AB=BA$

结合律：$A\cup (B\cup C)=(A\cup B)\cup C$，$A(BC)=AB(C)$

分配律：$A(B\cup C)=(AB)\cup (AC)$，$A\cup (BC)=(A\cup B)(A\cup C)$

对偶律：$\overline{A\cup B}=\overline{A}\overline{B}$，$\overline{AB}=\overline{A}\cup \overline{B}$

其它：$A-B=A\overline{B}$，$A=(AB)\cup (A\overline{B})$

关于$A$与$\overline{A}$，其实很好地理解的！如果这两个事件都发生，我们可以用以下语言来描述，$A$：事件A发生。$\overline{A}$：事件A不发生（也就是事件$\overline{A}$发生）。

事件的概率

首先开设！设$E$是随机试验，$\Omega$是其样本空间。

对每个事件$A$，定义一个实数$P(A)$与之对应（注意，此时的$P(A)$还不能算作概率，需满足下面条件才行），若$P(A)$满足下面条件：

对于每个事件$A$，均有$P(A)\ge 0$。（概率总不可能为负的吧）

$P(\Omega )=1$

若任意不相同的两事件$A_1,A_2$互斥，均有$P(A_1\cup A_2)=P(A_1)+P(A_2)$

则称$P(A)$为事件$A$的概率。

☁️ 概率的性质

$P(\varnothing )=0$

两两互斥事件之和的概率等于它们各自的概率之和，即上面的条件3

对任意事件$A$，均有$P(\overline{A})=1-P(A)$

对两个事件$A$和$B$，❗️若$A\subset B$，则有$P(B-A)=P(B)-P(A)$

对任意两个事件$A$和$B$，有$P(A\cup B)=P(A)+P(B)-P(AB)$

PS：一定要注意第4、5条两个事件$A$、$B$的限制不同！！！

古典概率模型

关于“古典”这俩字啊，我一直都很好奇为啥叫古典，通过度娘加上我自己的理解应该是因为年代久远吧。嗯，就是这样。

那么继续总结概念，后面还有案例等着我用C语言实现呢！

何为古典概率模型？

如果试验$E$的结果只有有限种，且每种结果发生的可能性相同，则称这样的试验模型为等可能概率模型或古典概率模型，简称等可能概型或古典模型。

假设试验$E$的样本空间$\Omega =\{w_1,..,w_n\}$，根据上述概念，则有$P(w_1)=...=P(w_n)=\frac{1}{n}$

在前面的基本概念中，我们提到了基本事件，假设事件$A$包含了若干个基本事件，$P(A)=\frac{A包含的基本事件数}{基本事件总数}$。

ok，知识点大致已经记录清楚了。进一步就根据案例用C语言来学习吧！

C语言案例实现

先从简单的开始。（以下都是建立在古典概率模型的前提下），其中n为基本事件总数，需要先求出来。

1. 掷一颗匀称骰子，设A表示所掷结果为“四点或五点”，B表示所掷结果为“偶数点”。求$P(A)$和$P(B)$.

#include 
int main()
{
	//基本事件总数
	int n = 6;
	//给事件A、B赋初值
	//当找到满足条件的基本事件的时候A、B就加1
	int A = 0,B = 0;			
	for(int i = 1 ; i <= 6 ; i++)
	{
		if(i % 2 == 0)
			B++;
		if(i == 4 || i == 5)
			A++;
	}
	printf("The probability of incident A is :%d/%d.\n",A,n);
	printf("The probability of incident B is :%d/%d.\n",B,n);
	return 0;
}

2. 将一枚均匀硬币抛掷三次，设事件A表示“恰有两次出现正面”，事件B表示“至少有一次出现正面”，求$P(A)$和$P(B)$.

#include 
int main()
{
	//基本事件总数
	int n = 8;
	//初始化事件A、B的概率
	int A = 0,B = 0;
	//pos表示出现正面的次数
	int pos = 0;
	//用0表示反面，1表示正面
	for(int i = 0 ; i <= 1 ; i++)
	{
		//第一次如果是正面则加1
		if(i == 1)
			pos++;
		for(int j = 0 ; j <= 1 ; j++)
		{
			//第二次如果是正面则加1
			if(j == 1)
				pos++;
			for(int k = 0 ; k <= 1 ; k++)
			{
				//第三次如果是正面则加1
				if(k == 1)
					pos++;
				//我们只有在三次抛硬币的结果都确定了，才能判断事件是否发生
				if(pos >= 1)
					B++;
				if(pos == 2)
					A++;
			}
			//第三层循环（第三次抛硬币）结束后，将pos置为0
			//为什么要置pos为0？
			//因为第三次抛硬币是在第二次确定了的情况下
			//如果第二次的结果改变，则第三次的结果又要重新考虑
			//相当于是控制变量法，否则pos会出现大于3的情况
			pos = 0;
		}
		//第二层循环（第二次抛硬币）结束后，将pos置为0
		//理由同上
		pos = 0;
	}
	printf("The probability of incident A is : %d/%d\n",A,n);
	printf("The probability of incident B is : %d/%d",B,n);
	return 0 ;
}

其中，事件B发生的概率为$\frac{7}{8}$，满足事件B的结果太多了。那么它剩下的$\frac{1}{8}$表示的是什么事件呢？

它表示的是“三次抛硬币三次都是反面”，也就是$\overline{B}$，意思是事件B不发生的概率。那么$P(B)=1-P(\overline{B})$，排除了B不发生的概率，那么剩下的一定就是B发生的概率了。同样，每一事件的概率的算法都有多种，我们呢就需要尽量去用最简便的方法。go on！

插播一个知识点~~~

☁️ 排列组合

排列：从n个不同元素中，任取m（m≤n）个不同的元素按照一定的顺序排成一列，有$A_n^m$种排法。规定$!0=1$$$A_n^m=n(n-1)(n-2)\cdot \cdot \cdot (n-m+1)=\frac{n!}{(n-m)!}$$
这个其实也很好理解，加上n，这个乘法算式一共有m个数。例如$A_5^3=5\times 4\times 3=60$，就有m=3个数。

用C语言来实现就是（可自行代入数据测试）：

#include 
int Arrange(int n,int m)
{
	int sum = 1;
	for( ; m > 0 ; m--)
	{
		sum *= n--;
	}
	return sum;
}

int main()
{
	int a = arrange(6,0);
	printf("%d",a);
	return 0;	
}

组合：从n个不同元素中，任取m(m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合，有$C_n^m$种组合。$$C_n^m=\frac{A_n^m}{m!}=\frac{n!}{m!(n-m)!}$$

用C语言来实现就是：

#include 
int Combination(int n,int m)
{
	int sum = 1,p = 1;
	for( ; m > 0 ; m--)
	{
		sum *= n--;
		p *= m;
	}
	
	return sum/p;
}

int main()
{
	int a = Combination(15,2);
	printf("%d",a);
	return 0;	
}

好了，知识预备完毕，继续做例题。

❗️当基本事件总数较小时，我们还可以列出全部可能性来进行筛查，但当基本事件总数很大的时候，我们列出全部可能性就很麻烦，计算量很大。那么这时，我们就会用到排列组合了。它也是建立在古典概型的基础上的。

3. 货架上有外观相同的商品15件，其中12件来自甲地，3件来自乙地，现从15件商品中随机地抽取两件，求这两件商品来自同一地的概率。

#include 
int Combination(int n,int m)
{
	int sum = 1,p = 1;
	for( ; m > 0 ; m--)
	{
		sum *= n--;
		p *= m;
	}
	
	return sum/p;
}
int main()
{
	//基本事件总数n
	int n = Combination(15,2);
	//a代表两件商品出自甲地，b代表两件商品出自乙地
	int a = Combination(12,2);
	int b = Combination(3,2);
	//a,b互斥，所以它们的概率能相加
	printf("The probability of the incident is : %d/%d",a + b,n);
	return 0;
}

4. 有白色乒乓球12只，黄色乒乓球3只，现将它们随机地分装在3个盒中，每盒装5只。设事件A表示“每盒中恰有一只黄色球”，事件B表示三只黄色球都在同一盒中“，求$P(A)$和$P(B)$.

其中基本事件总数为$C_{15}^5{C}_{10}^5{C}_5^5$。

int main()
{
	//基本事件总数
	int n = Combination(15,5) * Combination(10,5) * Combination(5,5);
	//三个黄色球先分别装入三个盒子中
	int A = Arrange(3,3) * Combination(12,4) * Combination(8,4) * Combination(4,4);
	//三个黄色球先装入一个盒子，再装入两个，剩下的再装到另外两个盒子里
	int B = 3 * Combination(12,2) * Combination(10,5) * Combination(5,5);
	printf("The probability of the incident is : %d/%d.\n",A,n);
	printf("The probability of the incident is : %d/%d.",B,n);
	return 0;	
}

什么！！！这个结果居然如此之大，看着就不舒服。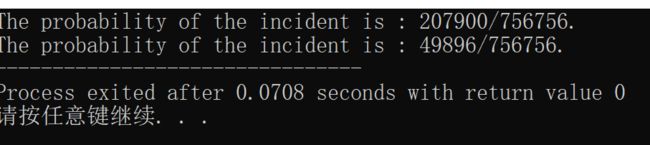
这个我当然不能忍了，赶紧又写了一个约分函数。

约分函数：

#include 

void Abbreviation(long int *a)
{
	while(a[0] % 2 == 0 && a[1] % 2 == 0)
	{
		a[0] /= 2;
		a[1] /= 2;
	}
	
	for(int i = 3 ;i <= a[1] / 2 ; i += 2)
	{
		while(a[0] % i == 0 && a[1] % i == 0)
		{
			a[0] /= i;
			a[1] /= i;
		}
	}
}

int main()
{
	long int a[2] = {207900,756756};
	Abbreviation(a);
	printf("%d/%d",a[0],a[1]);
	return 0;
}

然后我们在原函数调用这个这个函数就可以了。

这一次的学习就到这里，如有不足之处还请各位斧正。