神经网络笔记1-三层BP神经网络
神经网络笔记1-三层BP神经网络
-
- 神经网络性质简介
- 信息正向传输
- 预期神经网络的获得
-
- 误差反向更新(输出层→隐藏层)
- 误差反向更新(隐藏层→输入层)
- 伪代码实现
-
-
- 训练函数
- 测试函数,用训练好的神经网络预测
-
- 手写数字识别举例
-
- 识别单个数字举例
- 识别全部数字举例
- 主程序框架搭建
神经网络性质简介
神经网络是用几个层之间建立联系,正像一个黑匣子一样,例如有一个机器,带皮的苹果进到这个黑匣子里,输出变成一个削完皮的苹果,带皮的香蕉进去自动变成剥完皮的香蕉。那么这个黑匣子就是一个剥皮的“网络”。在代码中我们也有类似的神经网络,这个神经网络就类似于我们大脑的神经元,神经网络包含很多层,每一层都有很多神经元,神经元的输入可能和之前很多神经元的输出都有联系。这个联系的紧密程度我们可以用一个权重值来表示。每两层之间的所有权重值可以构成一个矩阵,叫它传输矩阵,它建立了两层神经元之间的联系。
神经网络包含多个层:输入层、隐藏层、输出层。一般来讲它们之间的数据是逐次传输的。
例如我们希望有一个神经网络,输入一张图片,这个神经网络就能够输出这张图片上写着什么。那么这个神经网络就是我们要寻找的识别网络。我们可以将图片转化成一个向量,将向量的每一个元素作为输入层的不同神经元的输入,这样在输入层和隐藏层的传输矩阵的作用下,图片的数据经过变换来到了隐含层。同理,隐含层将数据通过隐藏层和输出层的传输矩阵作用到输出层的不同神经元上,这样我们期待的输出就是图片上写的内容。
下文将详细阐述神经网络的数据传输过程和如何构造预期的神经网络。
输入层的层数要与输入一致,输出层的层数要与期望输出个数一致。理论上隐藏层可以设置多个,并且单元数没有限制。但是本文只讨论三层的神经网络,三层BP神经网络可以逼近任意连续的函数,简单易行,可靠性好,故只选择一个隐含层。
设隐藏层单元个数为 p p p,输入层单元个数为 m m m,输出层单元个数为 n n n,隐藏层数不是越多越好,在用神经网络逼近函数的时候,保证准确率高,有经验公式:
p = 5 + m + n ± 5 p=5+\sqrt{m+n}\pm 5 p=5+m+n±5
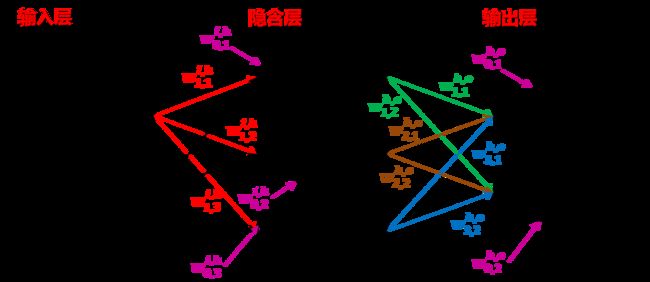
为了方便统一表述,我们用1,2,3来分别代表输入层、隐藏层、输出层。
设第 k k k层的输入为向量 r k \mathbf{r}^{k} rk,其第 i i i个单元的值为 r i k r_{i}^{k} rik
第 k k k层的输出为向量 a k \mathbf{a}^{k} ak,其第 i i i个单元的值为 a i k a_{i}^{k} aik
第 k k k层第 i i i个输出单元到第 k + 1 k+1 k+1层第 j j j个输入单元的传输常数为 w i , j k w_{i,j}^{k} wi,jk,构成矩阵 W k = [ w i , j k ] T \mathbf{W}^{k}=[ w_{i,j}^{k} ]^{T} Wk=[wi,jk]T,其中 i i i从 0 0 0开始,有一个常数项输入,第一列就是常数项偏置列。
注意矩阵 W k \mathbf{W}^{k} Wk是按照角标转置后排列的。
信息正向传输
传输过程可以写成如下表达:
r j k + 1 = ∑ i = 0 w i , j k a i k r_{j}^{k+1} =\sum_{i=0} w_{i,j}^{k} a_{i}^{k} rjk+1=i=0∑wi,jkaik
这个式子的意义是某一层的某一个单元与前一层的所有单元都有关,而其中的权重值为 w i , j k w_{i,j}^{k} wi,jk
矩阵写法为:
r k + 1 = W k [ 1 . . . a k ] \mathbf{r} ^{k+1}=\mathbf{W} ^{k} \begin{bmatrix} 1\\ ...\\ \mathbf{a} ^{k} \end{bmatrix} rk+1=Wk⎣⎡1...ak⎦⎤
其中 a 0 k = 1 a_{0}^{k}=1 a0k=1这一项说明传输矩阵有一列作为常数项偏置作为某一个单元的输入。
在每层的输入和输出中间有一个传递关系:
采用核函数
g ( x ) = 1 1 + e − x g(x)=\frac{1}{1+e^{-x} } g(x)=1+e−x1
该函数为LOGISTIC函数,其具有微分性质:
g ′ ( x ) = g ( x ) ( 1 − g ( x ) ) g'(x)=g(x)(1-g(x)) g′(x)=g(x)(1−g(x))
这个函数就是每个单元对输入的数据都进行了一次归一化处理,这使得每层的输出都是 ( 0 , 1 ) (0,1) (0,1)的概率数。故有
a k = g ( r k ) \mathbf{a} ^{k} =g(\mathbf{r} ^{k} ) ak=g(rk)
设输入向量为 x = [ x 1 , x 2 , . . . , x m ] T \mathbf{x} =[x_{1} ,x_{2} ,...,x_{m} ]^{T} x=[x1,x2,...,xm]T,输出向量为 y = [ y 1 , y 2 , . . . , y n ] T \mathbf{y} =[y_{1} ,y_{2} ,...,y_{n} ]^{T} y=[y1,y2,...,yn]T输出向量与最后一层的输出同阶数
有:
r 1 = x \mathbf{r}^{1}=\mathbf{x} r1=x
我们的目标就是通过神经网络的输出 a 3 \mathbf{a} ^{3} a3去逼近输出 y \mathbf{y} y
预期神经网络的获得
误差反向更新(输出层→隐藏层)
定义损失函数
L = ∥ y − a 3 ∥ 2 = ∑ i ( y i − a i 3 ) 2 L=\left \| \mathbf{y}- \mathbf{a} ^{3} \right \| ^{2} =\sum_{i} (y_{i} -a_{i}^{3} )^{2} L=∥∥y−a3∥∥2=i∑(yi−ai3)2
这个函数就表示训练前的网络在对输入数据处理得到的输出与期望输出的偏离程度。我们希望这个损失函数越小越好。因此理论上我们想逼近损失函数的极小值(也就是0)。损失函数内部有很多参数,我们需要更新的参数就是 w i , j k w_{i,j}^{k} wi,jk
这就需要梯度下降法来不断更新这些权重值。
梯度下降法可以参考我之前写的文章:梯度下降法线性回归模拟:https://blog.csdn.net/m0_53253879/article/details/123811100?spm=1001.2014.3001.5501
设迭代次数为 l l l,由梯度下降法公式
w i , j k ← w i , j k − α ∂ L ∂ w i , j k w_{i,j}^{k} ←w_{i,j}^{k} -\alpha \frac{\partial L}{\partial w_{i,j}^{k}} wi,jk←wi,jk−α∂wi,jk∂L
先更新第 2 2 2层到第 3 3 3层的 w i , j 2 w_{i,j}^{2} wi,j2:
∂ L ∂ w α , β 2 = ∂ ∑ i ( y i − a i 3 ) 2 ∂ w α , β 2 = ∂ ∑ i ( y i − g ( r i 3 ) ) 2 ∂ w α , β 2 { \frac{\partial L}{\partial w_{\alpha, \beta }^{2}}= \frac{\partial \sum_{i} (y_{i} -a_{i}^{3} )^{2}}{\partial w_{\alpha, \beta}^{2}}= \frac{\partial \sum_{i} (y_{i} -g(r_{i}^{3}) )^{2}}{\partial w_{\alpha, \beta}^{2}}} ∂wα,β2∂L=∂wα,β2∂∑i(yi−ai3)2=∂wα,β2∂∑i(yi−g(ri3))2
= ∂ ∑ i ( y i − g ( ∑ j = 0 w j , i 2 a j 2 ) ) 2 ∂ w α , β 2 = ∂ ( y α − g ( ∑ j = 0 w j , β 2 a j 2 ) ) 2 ∂ w α , β 2 {= \frac{\partial \sum_{i} (y_{i} -g(\sum_{j = 0} w_{j,i}^{2} a_{j}^{2}) )^{2}}{\partial w_{\alpha, \beta}^{2}}= \frac{\partial(y_{\alpha } -g(\sum_{j = 0} w_{j ,\beta}^{2} a_{j}^{2}) )^{2}}{\partial w_{\alpha, \beta}^{2}}} =∂wα,β2∂∑i(yi−g(∑j=0wj,i2aj2))2=∂wα,β2∂(yα−g(∑j=0wj,β2aj2))2
= − 2 ( y α − g ( ∑ j = 0 w j , β 2 a j 2 ) ) g ′ ( ∑ j = 0 w α , j 2 a j 2 ) ) a α 2 \small =-2(y_{\alpha } -g(\sum_{j = 0} w_{j ,\beta}^{2} a_{j}^{2}) )g'(\sum_{j = 0} w_{\alpha ,j}^{2} a_{j}^{2}) )a_{\alpha }^{2} =−2(yα−g(∑j=0wj,β2aj2))g′(∑j=0wα,j2aj2))aα2
= − 2 ( y α − g ( ∑ j = 0 w j , β 2 a j 2 ) ) g ( ∑ j = 0 w j , β 2 a j 2 ) ) ( 1 − g ( ∑ j = 0 w j , β 2 a j 2 ) ) ) a α 2 \small =-2(y_{\alpha } -g(\sum_{j = 0} w_{j ,\beta}^{2} a_{j}^{2}) )g(\sum_{j = 0} w_{j ,\beta}^{2} a_{j}^{2}) )(1-g(\sum_{j = 0} w_{j ,\beta}^{2} a_{j}^{2}) ))a_{\alpha }^{2} =−2(yα−g(∑j=0wj,β2aj2))g(∑j=0wj,β2aj2))(1−g(∑j=0wj,β2aj2)))aα2
因此:
− 1 2 ∂ L ∂ w i , j 2 = ( y j − a j 3 ) a j 3 ( 1 − a j 3 ) a i 2 {\normalsize -\frac{1}{2} \frac{\partial L}{\partial w_{i, j }^{2}}=(y_{j } -a_{j}^{3})a_{j}^{3}(1-a_{j}^{3}) a_{i }^{2}} −21∂wi,j2∂L=(yj−aj3)aj3(1−aj3)ai2
记:
Δ i 2 = ( y i − a i 3 ) a i 3 ( 1 − a i 3 ) Δ k = [ Δ 0 k , Δ 1 k , . . . Δ n k ] T A 3 = d i a g ( a 1 3 , a 2 3 , . . . , a n 3 ) a ~ 2 = [ 1 . . . a 2 ] \begin{matrix} \Delta _{i}^{2}=(y_{i } -a_{i}^{3})a_{i}^{3}(1-a_{i}^{3})\\ \mathbf{\Delta }^{k}=[\Delta _{0}^{k} ,\Delta _{1}^{k},...\Delta _{n}^{k} ]^{T} \\ \mathbf{A} ^{3} =diag(a_{1}^{3} ,a_{2}^{3},...,a_{n}^{3})\\ \tilde{\mathbf{a}} ^{2} = \begin{bmatrix} 1\\ ...\\ \mathbf{a} ^{2} \end{bmatrix} \end{matrix} Δi2=(yi−ai3)ai3(1−ai3)Δk=[Δ0k,Δ1k,...Δnk]TA3=diag(a13,a23,...,an3)a~2=⎣⎡1...a2⎦⎤
故有:
− 1 2 ∂ L ∂ w i , j 2 = Δ j 2 a i 2 -\frac{1}{2} \frac{\partial L}{\partial w_{i, j }^{2}}=\Delta _{j}^{2}a_{i }^{2} −21∂wi,j2∂L=Δj2ai2
Δ 2 = A 3 ( I − A 3 ) ( y − a 3 ) w i , j 2 ← w i , j 2 − α Δ j 2 a i 2 \begin{matrix} \mathbf{\Delta }^{2}=\mathbf{A} ^{3}(\mathbf{I}-\mathbf{A} ^{3})(\mathbf{y}- \mathbf{a} ^{3} ) \\ w_{i,j}^{2} ←w_{i,j}^{2} -\alpha \Delta _{j}^{2}a_{i }^{2} \end{matrix} Δ2=A3(I−A3)(y−a3)wi,j2←wi,j2−αΔj2ai2
写成矩阵形式有
W 2 ← W 2 − α Δ 2 ( a ~ 2 ) T \mathbf{W} ^{2} ←\mathbf{W} ^{2} -\alpha \mathbf{\Delta }^{2}(\tilde{\mathbf{a}} ^{2})^{T} W2←W2−αΔ2(a~2)T
这里需要注意的是 − 1 2 ∂ L ∂ w i , j 2 -\frac{1}{2} \frac{\partial L}{\partial w_{i, j }^{2}} −21∂wi,j2∂L中的 − 1 2 -\frac{1}{2} −21被学习率 α \alpha α吸收了,因为学习率是一个可变参数
误差反向更新(隐藏层→输入层)
− 1 2 ∂ L ∂ w α , β 1 = ∑ i ( y j − a j 3 ) a j 3 ( 1 − a j 3 ) a i 2 w j , i 2 ∑ j ∂ a j 2 ∂ w α , β 1 -\frac{1}{2} \frac{\partial L}{\partial w_{\alpha ,\beta }^{1}}= \sum_{i} (y_{j } -a_{j}^{3})a_{j}^{3}(1-a_{j}^{3}) a_{i }^{2}w_{j,i}^{2}\sum_{j}\frac{\partial a_{j}^{2} }{\partial w_{\alpha ,\beta }^{1} } −21∂wα,β1∂L=i∑(yj−aj3)aj3(1−aj3)ai2wj,i2j∑∂wα,β1∂aj2
上面这个求导式子相当繁琐,根据链式法则,我们只给出结果如下:
− 1 2 ∂ L ∂ w i , j 1 = a j 2 ( 1 − a j 2 ) a i 1 ∑ k w j k 2 Δ k 2 -\frac{1}{2} \frac{\partial L}{\partial w_{i, j }^{1}}=a_{j}^{2}(1-a_{j}^{2}) a_{i }^{1}\sum_{k} w_{jk}^{2} \Delta _{k}^{2} −21∂wi,j1∂L=aj2(1−aj2)ai1k∑wjk2Δk2
设
Δ j 1 = a j 2 ( 1 − a j 2 ) ∑ k w j k 2 Δ k 2 A 2 = d i a g ( a 1 2 , a 2 2 , . . . , a n 2 ) a ~ 1 = [ 1 . . . a 1 ] \begin{matrix} \Delta _{j}^{1} =a_{j}^{2}(1-a_{j}^{2})\sum_{k} w_{jk}^{2} \Delta _{k}^{2} \\ \mathbf{A} ^{2} =diag(a_{1}^{2} ,a_{2}^{2},...,a_{n}^{2}) \end{matrix}\\ \tilde{\mathbf{a}} ^{1} = \begin{bmatrix} 1\\ ...\\ \mathbf{a} ^{1} \end{bmatrix} Δj1=aj2(1−aj2)∑kwjk2Δk2A2=diag(a12,a22,...,an2)a~1=⎣⎡1...a1⎦⎤
在上面几个式子中, W 2 \mathbf{W} ^{2} W2的常数偏置列在求导中消失了,我们定义矩阵 W ~ 2 \tilde{\mathbf{W}} ^{2} W~2为 W 2 \mathbf{W} ^{2} W2删除偏置列(第一列)并取转置之后的矩阵。
故有:
Δ 1 = A 2 ( I − A 2 ) W ~ 2 Δ 2 \mathbf{\Delta } ^{1} =\mathbf{A} ^{2} (\mathbf{I}- \mathbf{A} ^{2})\tilde{\mathbf{W}} ^{2} \mathbf{\Delta }^{2} Δ1=A2(I−A2)W~2Δ2
W 1 ← W 1 − α Δ 1 ( a ~ 1 ) T \mathbf{W} ^{1} ←\mathbf{W} ^{1} -\alpha \mathbf{\Delta }^{1}(\tilde{\mathbf{a}} ^{1})^{T} W1←W1−αΔ1(a~1)T
再经过不断的更新, w i , j k w_{i,j}^{k} wi,jk逐渐变成我们期待的网络,进而对于每个输入,都可以达到我们预期的输出。
但是这里需要强调的是,该神经网络不是对某一个样本输入一直进行训练达到损失函数的收敛,而是大量的数据作为输入样本依次通过神经网络,每个样本输入都会对神经网络进行一次训练。在大量样本都对该神经网络进行训练之后,神经网络对于某个样本的输出就能有一个大体的判断。所有样本也可以对神经网络进行多次训练,但是损失函数不会收敛到0,而是会在一定范围内进行波动。
伪代码实现
训练函数
从文件获取 x = [ x 1 , x 2 , . . . , x m ] T \mathbf{x} =[x_{1} ,x_{2} ,...,x_{m} ]^{T} x=[x1,x2,...,xm]T
从文件获取 y = [ y 1 , y 2 , . . . , y n ] T \mathbf{y} =[y_{1} ,y_{2} ,...,y_{n} ]^{T} y=[y1,y2,...,yn]T
中间隐藏层层数 p = 5 + m + n p=5+\sqrt{m+n} p=5+m+n
第一层输入 r 1 = x ∈ R m × 1 \mathbf{r}^{1}=\mathbf{x}\in R^{m\times 1} r1=x∈Rm×1
第一层输出 a 1 ∈ R m × 1 \mathbf{a}^{1}\in R^{m\times 1} a1∈Rm×1
第二层输入 r 2 ∈ R p × 1 \mathbf{r}^{2}\in R^{p\times 1} r2∈Rp×1
第二层输出 a 2 ∈ R p × 1 \mathbf{a}^{2}\in R^{p\times 1} a2∈Rp×1
第三层输入 r 3 ∈ R n × 1 \mathbf{r}^{3}\in R^{n\times 1} r3∈Rn×1
第三层输出 a 3 ∈ R n × 1 \mathbf{a}^{3}\in R^{n\times 1} a3∈Rn×1
第一层到第二层传递矩阵 W 1 ∈ R p × ( m + 1 ) \mathbf{W} ^{1}\in R^{p\times (m+1)} W1∈Rp×(m+1)
第二层到第三层传递矩阵 W 2 ∈ R n × ( p + 1 ) \mathbf{W} ^{2}\in R^{n\times (p+1)} W2∈Rn×(p+1)
增广向量 a ~ 1 = [ 1 . . . a 1 ] ∈ R ( m + 1 ) × 1 \tilde{\mathbf{a}} ^{1} = \begin{bmatrix} 1\\ ...\\ \mathbf{a} ^{1} \end{bmatrix}\in R^{(m+1)\times 1} a~1=⎣⎡1...a1⎦⎤∈R(m+1)×1
增广向量 a ~ 2 = [ 1 . . . a 2 ] ∈ R ( p + 1 ) × 1 \tilde{\mathbf{a}} ^{2} = \begin{bmatrix} 1\\ ...\\ \mathbf{a} ^{2} \end{bmatrix}\in R^{(p+1)\times 1} a~2=⎣⎡1...a2⎦⎤∈R(p+1)×1
定义函数 g ( x ) = 1 1 + e − x g(x)=\frac{1}{1+e^{-x} } g(x)=1+e−x1
定义学习参数 α = \alpha= α=
定义迭代次数 k = 0 k=0 k=0
损失函数赋初值 L ( 0 ) = ∥ y − ( a 3 ) ∥ 2 L^{(0)}=\left \| \mathbf{y}- (\mathbf{a} ^{3}) \right \| ^{2} L(0)=∥∥y−(a3)∥∥2
第一层到第二层传递矩阵赋初值 ( W 1 ) (\mathbf{W} ^{1}) (W1)
第二层到第三层传递矩阵赋初值 ( W 2 ) (\mathbf{W} ^{2}) (W2)
(正向更新)
a 1 = g ( r 1 ) \mathbf{a} ^{1} =g(\mathbf{r} ^{1} ) a1=g(r1)
( r 2 ) ( 0 ) = ( W 1 ) ( 0 ) a ~ 1 (\mathbf{r} ^{2})^{(0)}=(\mathbf{W} ^{1})^{(0)}\tilde{\mathbf{a}} ^{1} (r2)(0)=(W1)(0)a~1
( a 2 ) ( 0 ) = g ( r 2 ) ( 0 ) (\mathbf{a} ^{2})^{(0)} =g(\mathbf{r} ^{2} )^{(0)} (a2)(0)=g(r2)(0)
( a ~ 2 ) ( 0 ) = [ 1 . . . ( a 2 ) ( 0 ) ] (\tilde{\mathbf{a}} ^{2})^{(0)} = \begin{bmatrix} 1\\ ...\\ \mathbf(\mathbf{a} ^{2})^{(0)} \end{bmatrix} (a~2)(0)=⎣⎡1...(a2)(0)⎦⎤
( r 3 ) ( 0 ) = ( W 2 ) ( 0 ) a ~ 2 (\mathbf{r} ^{3})^{(0)}=(\mathbf{W} ^{2})^{(0)}\tilde{\mathbf{a}} ^{2} (r3)(0)=(W2)(0)a~2
( a 3 ) ( 0 ) = g ( r 3 ) ( 0 ) (\mathbf{a} ^{3})^{(0)} =g(\mathbf{r} ^{3} )^{(0)} (a3)(0)=g(r3)(0)
( a ~ 3 ) ( 0 ) = [ 1 . . . ( a 3 ) ( 0 ) ] (\tilde{\mathbf{a}} ^{3})^{(0)} = \begin{bmatrix} 1\\ ...\\ \mathbf(\mathbf{a} ^{3})^{(0)} \end{bmatrix} (a~3)(0)=⎣⎡1...(a3)(0)⎦⎤
( A 2 ) ( 0 ) = d i a g ( ( a ~ 2 ) ( 0 ) ) (\mathbf{A} ^{2})^{(0)} =diag((\tilde{\mathbf{a}} ^{2})^{(0)}) (A2)(0)=diag((a~2)(0))
( A 3 ) ( 0 ) = d i a g ( ( a ~ 3 ) ( 0 ) ) (\mathbf{A} ^{3})^{(0)} =diag((\tilde{\mathbf{a}} ^{3})^{(0)}) (A3)(0)=diag((a~3)(0))
( Δ 2 ) ( 0 ) = ( A 3 ) ( 0 ) ( I − ( A 3 ) ( 0 ) ) ( y − ( a 3 ) ( 0 ) ) (\mathbf{\Delta }^{2})^{(0)}=(\mathbf{A} ^{3})^{(0)}(\mathbf{I}-(\mathbf{A} ^{3})^{(0)})(\mathbf{y}- (\mathbf{a} ^{3})^{(0)} ) (Δ2)(0)=(A3)(0)(I−(A3)(0))(y−(a3)(0))
( Δ 1 ) ( 0 ) = ( A 2 ) ( 0 ) ( I − ( A 2 ) ( 0 ) ) W ~ 2 ( Δ 2 ) ( 0 ) (\mathbf{\Delta }^{1})^{(0)}=(\mathbf{A} ^{2})^{(0)} (\mathbf{I}- (\mathbf{A} ^{2})^{(0)})\tilde{\mathbf{W}} ^{2}(\mathbf{\Delta }^{2})^{(0)} (Δ1)(0)=(A2)(0)(I−(A2)(0))W~2(Δ2)(0)
损失函数赋初值 L ( 0 ) = ∥ y − ( a 3 ) ( 0 ) ∥ 2 L^{(0)}=\left \| \mathbf{y}- (\mathbf{a} ^{3})^{(0)} \right \| ^{2} L(0)=∥∥y−(a3)(0)∥∥2
循环,按样本数对每个样本执行如下操作
(误差反向更新)
W 2 ← W 2 − α Δ 2 ( a ~ 2 ) T \mathbf{W} ^{2} ←\mathbf{W} ^{2} -\alpha \mathbf{\Delta }^{2}(\tilde{\mathbf{a}} ^{2})^{T} W2←W2−αΔ2(a~2)T
W 1 ← W 1 − α Δ 1 ( a ~ 1 ) T \mathbf{W} ^{1} ←\mathbf{W} ^{1} -\alpha \mathbf{\Delta }^{1}(\tilde{\mathbf{a}} ^{1})^{T} W1←W1−αΔ1(a~1)T
(正向传递)
r 2 = W 1 a ~ 1 \mathbf{r} ^{2}=\mathbf{W} ^{1}\tilde{\mathbf{a}} ^{1} r2=W1a~1
a 2 = g ( r 2 ) \mathbf{a} ^{2} =g(\mathbf{r} ^{2} ) a2=g(r2)
a ~ 2 = [ 1 . . . a 2 ] \tilde{\mathbf{a}} ^{2}= \begin{bmatrix} 1\\ ...\\ \mathbf{a} ^{2} \end{bmatrix} a~2=⎣⎡1...a2⎦⎤
r 3 = W 2 a ~ 2 \mathbf{r} ^{3}=\mathbf{W} ^{2}\tilde{\mathbf{a}} ^{2} r3=W2a~2
a 3 = g ( r 3 ) \mathbf{a} ^{3} =g(\mathbf{r} ^{3} ) a3=g(r3)
a ~ 3 = [ 1 . . . a 3 ] \tilde{\mathbf{a}} ^{3} = \begin{bmatrix} 1\\ ...\\ \mathbf{a} ^{3} \end{bmatrix} a~3=⎣⎡1...a3⎦⎤
A 2 = d i a g ( a 2 ) \mathbf{A} ^{2} =diag(\mathbf{a} ^{2}) A2=diag(a2)
A 3 = d i a g ( a 3 ) \mathbf{A} ^{3} =diag(\mathbf{a} ^{3}) A3=diag(a3)
Δ 2 = A 3 ( I − A 3 ) ( y − a 3 ) \mathbf{\Delta }^{2}=\mathbf{A} ^{3}(\mathbf{I}-\mathbf{A} ^{3})(\mathbf{y}- \mathbf{a} ^{3}) Δ2=A3(I−A3)(y−a3)
Δ 1 = A 2 ( I − A 2 ) W ~ 2 Δ 2 \mathbf{\Delta }^{1}=\mathbf{A} ^{2}(\mathbf{I}- \mathbf{A} ^{2})\tilde{\mathbf{W}} ^{2} \mathbf{\Delta }^{2} Δ1=A2(I−A2)W~2Δ2
L = ∥ y − a 3 ∥ 2 L=\left \| \mathbf{y}- \mathbf{a} ^{3} \right \| ^{2} L=∥∥y−a3∥∥2
测试函数,用训练好的神经网络预测
a 1 = g ( x ) \mathbf{a} ^{1} =g(\mathbf{x} ) a1=g(x)
a ~ 1 = [ 1 . . . a 1 ] \tilde{\mathbf{a}} ^{1} = \begin{bmatrix} 1\\ ...\\ \mathbf{a} ^{1} \end{bmatrix} a~1=⎣⎡1...a1⎦⎤
a 2 = g ( W 1 a ~ 1 ) \mathbf{a} ^{2}=g(\mathbf{W} ^{1} \tilde{\mathbf{a}} ^{1}) a2=g(W1a~1)
a ~ 2 = [ 1 . . . a 2 ] \tilde{\mathbf{a}} ^{2} = \begin{bmatrix} 1\\ ...\\ \mathbf{a} ^{2} \end{bmatrix} a~2=⎣⎡1...a2⎦⎤
y = g ( W 2 a ~ 2 ) \mathbf{y}=g(\mathbf{W} ^{2} \tilde{\mathbf{a}} ^{2}) y=g(W2a~2)
(总公式: y = g ( W 2 [ 1 . . . g ( W 1 [ 1 . . . g ( x ) ] ) ] \mathbf{y}=g(\mathbf{W} ^{2} \begin{bmatrix} 1\\ ...\\ g(\mathbf{W} ^{1} \begin{bmatrix} 1\\ ...\\ \mathbf g(\mathbf{x} ) \end{bmatrix}) \end{bmatrix} y=g(W2⎣⎢⎢⎢⎢⎡1...g(W1⎣⎡1...g(x)⎦⎤)⎦⎥⎥⎥⎥⎤)
返回 y \mathbf{y} y
手写数字识别举例
手写数字的训练集下载链接如下:
手写数字识别训练集:百度网盘分享https://pan.baidu.com/s/1A61uqPB_TTfyJ8sT4OqKIw?pwd=8f7a
每张图片是个 28 × 28 28\times 28 28×28像素的图片,
![]()
将这个图片作为输入需要将图片导入Python并形成归一化灰度矩阵
新建文件NeuralClass.py,在该文件中编写我们所需要的函数
把数据集放置到Python文件夹里,读取数据的函数如下:
from PIL import Image
# 输入图片,生成归一化灰度矩阵(黑色为1)
def get_gray_mt(pic_root):
img = Image.open(pic_root) # 读取图片
img = img.convert('L') # 灰度化
cols, rows = img.size # 图像大小
Value = [[0] * cols for i in range(rows)] # 创建一个大小与图片相同的二维数组
for x in range(0, rows):
for y in range(0, cols):
img_array = np.array(img)
v = img_array[x, y] # 获取该点像素值
Value[x][y] = 255 - v # 取反色,存入数组
Value = np.array(Value)/255
return Value
该函数对于输入图片地址可以转化成一个矩阵。但对于神经网络的输入必须是一个列向量,因此还需要以下函数把矩阵转化成列向量,读取方式是按行读取,把输入矩阵的每一行首尾相连形成一个矩阵。
from math import *
import numpy as np
# 将矩阵转化为列向量
def vector_c(A):
cols, rows = A.shape
vec = A.reshape(1, cols * rows)
return np.array(vec[0])
Python提供的numpy库所提供的矩阵函数有限,因此我们需要手动编写某些特定需要的函数:
为了实现与有偏置项的 W 1 \mathbf{W} ^{1} W1和 W 2 \mathbf{W} ^{2} W2矩阵相乘,在每层的输出向量需要提供一个函数在向量头部加1形成增广向量:
# 求增广向量,头部添加1
def enlarge_vec(x):
a = np.ones((1, len(x) + 1))
for i in range(len(x)):
a[0][i+1] = x[i]
return a
# 将向量转化成对角矩阵
def vec_diag(x):
A = np.eye(len(x))
for i in range(len(x)):
A[i][i] = x[i]
return A
矩阵 W ~ 2 \tilde{\mathbf{W}} ^{2} W~2为 W 2 \mathbf{W} ^{2} W2删除偏置列(第一列)并取转置之后的矩阵,因此我们写出下面这个函数用来删除矩阵的某一列。
# 删除矩阵某一列的函数(输入矩阵, 需要删除的列数)
def dlt_c(A, c0):
r, c = A.shape
B = np.zeros((r, c - 1))
for i in range(r):
for j in range(c-1):
if j < c0:
B[i][j] = A[i][j]
elif j > c0:
B[i][j - 1] = A[i][j]
return B
最重要的每层的输入输出之间核函数LOGISTIC函数,可以对整个向量或矩阵中的每一个元素均取一遍函数。
# 核函数(LOGISTIC)
def sigmoid_vec(x):
return 1/(1+np.exp(-x))
识别单个数字举例
有了以上基础,我们可以定义如下神经网络类:
# 神经网络类
class Neural_NetWork3:
(下面的代码为逐次书写)
这个网络里面初始化包含输入的训练集,输入层,隐藏层,输出层的层数,还有传输矩阵的初始化,损失函数列表。当给定某个训练样本时可以更新传输矩阵训练网络
# 初始化
def __init__(self, input_x, Input_lyout):
self.x = input_x # 输入所有数据
self.ly_in = int(len(input_x[0][0])) # 输入层层数(784)
self.ly_out = Input_lyout # 输出层层数
self.ly_hid = int(sqrt(self.ly_in + self.ly_out) + 5) # 隐藏层层数
self.samplenum = int(len(input_x[0])) # 每个数字选取的样本数
self.Loss = [] # 损失函数列表(在训练中会存入变化情况)
# 输入层到隐藏层的传输矩阵,设置初值,在第一列设置偏置列
self.W1 = np.random.normal(0.0, 1 / sqrt(self.ly_in), (self.ly_hid, self.ly_in + 1))
# 隐藏层到输出层的传输矩阵,设置初值,在第一列设置偏置列
self.W2 = np.random.normal(0.0, 1 / sqrt(self.ly_hid), (self.ly_out, self.ly_hid + 1))
pass
为了保证迭代的稳定性,给出的 W 1 \mathbf{W} ^{1} W1和 W 2 \mathbf{W} ^{2} W2初值设定在 ( 0 , 1 m ) (0,\frac{1}{\sqrt{m} } ) (0,m1)和 ( 0 , 1 p ) (0,\frac{1}{\sqrt{p} } ) (0,p1)区间内的随机数。初值设定有时不能过大或者全为零,这样有可能导致训练时出现发散。
这里的 x \mathbf{x} x是一个三阶张量,其按次序的两个索引分别为[样本所表示数字的第几个样本] [样本表示的数字]
在训练单个数字的判断网络时,输出向量为一标量,当需要训练的目标数字样本进入神经网络时,目标输出量为 1 1 1,当其他样本通过该网络时,目标输出量为 0 0 0。在经过大量的样本训练后,网络就能够对某一个数字样本进行识别,在输出就会比较靠近1,当其他样本经过神经网络时,输出就会比较靠近 0 0 0。因此可以通过输出标量的值来判断是某个训练数字的概率。
- 单个数字判断
- 输出向量大于 0.5 0.5 0.5(判定预测“是”该数字)
- 输出向量小于 0.5 0.5 0.5(判定预测“不是”该数字)
将样本逐次通过该神经网络
参考伪代码可以写出训练函数如下:
# 神经网络的训练函数,训练某个数字的函数
def Neural_Train_num(self, pre_num, alpha=0.2):
for j in range(self.samplenum):
for i in range(10):
y = np.zeros((self.ly_out, 1))
y[0][0] = (i == pre_num)
W2_conv = dlt_c(self.W2, 0) # W2删除第一列
a1 = self.x[i][j]
a1_en = enlarge_vec(a1) # a1的增广向量,头部加1
r2 = np.dot(self.W1, a1_en.T) # 隐藏层输入向量
a2 = sigmoid_vec(r2) # 隐藏层输出向量
a2_en = enlarge_vec(a2) # a2的增广向量,头部加1
r3 = np.dot(self.W2, a2_en.T) # 输出层输入向量
a3 = sigmoid_vec(r3) # 输出层输出向量
A2 = vec_diag(a2) # 由a2生成对角矩阵
A3 = vec_diag(a3) # 由a3生成对角矩阵
self.Loss.append(abs(np.linalg.norm(y - a3)))
# 反向传递
Delta2 = np.dot(A3 - np.dot(A3, A3), y - a3)
Delta1 = np.dot(A2 - np.dot(A2, A2), W2_conv.T)
Delta1 = np.dot(Delta1, Delta2)
Del_W2 = np.dot(Delta2, a2_en)
Del_W1 = np.dot(Delta1, a1_en)
self.W2 = self.W2 + alpha * Del_W2
self.W1 = self.W1 + alpha * Del_W1
预测神经网络的正确性时,有如下逻辑:
在给定图片输入时:
- 若输出大于 0.5 0.5 0.5,且该图片表示的数字正好是之前给定的数字则表示预测成功
- 若输出小于 0.5 0.5 0.5,且该图片表示的数字不是之前给定的数字则表示预测成功
- 否则为预测失败
将所有样本通过该网络可以给出预测的正确率,这是衡量该神经网络优良性的重要指标。
写出如下函数:
# 预测某个数字的正确率,输入为某个想要预测的图片上显示的数字
def Neural_Rate_num(self, Predict_num):
ra = 0 # 预测正确样本数
rn = 0 # 计算样本总数
for i in range(self.samplenum):
for j in range(10):
rn += 1
a1 = self.x[j][i]
a1_en = enlarge_vec(a1) # a1的增广向量,头部加1
r2 = np.dot(self.W1, a1_en.T) # 隐藏层输入向量
a2 = sigmoid_vec(r2) # 隐藏层输出向量
a2_en = enlarge_vec(a2) # a2的增广向量,头部加1
r3 = np.dot(self.W2, a2_en.T) # 输出层输入向量
a3 = sigmoid_vec(r3) # 输出层输出向量
if j == Predict_num and np.linalg.norm(a3) > 0.5:
ra += 1
if j != Predict_num and np.linalg.norm(a3) < 0.5:
ra += 1
return ra / rn
下面这个函数用来判断单独某张图片的预测结果
# 测试单独某张图片预测结果,输出为是或否
def Neural_Predict_num(self, x_Pre):
a1 = x_Pre
a1_en = enlarge_vec(a1)
r2 = np.dot(self.W1, a1_en.T)
a2 = sigmoid_vec(r2)
a2_en = enlarge_vec(a2)
r3 = np.dot(self.W2, a2_en.T)
a3 = sigmoid_vec(r3)
print(a3)
if a3[0] > 0.5:
return True
else:
return False
识别全部数字举例
识别全部数字时只需要把输出向量的阶数改为 10 10 10即可,每一行表示某一个数字的期望输出列。当需要训练的目标数字样本进入神经网络时,目标输出量对应的行为 1 1 1,例如一个表示0的图片输入时,目标输出的第一行为1,其余为0;一个表示1的图片输入时,目标输出的第二行为1,其余为0,以此类推。
写出预测全部数字的训练函数如下:
# 神经网络的训练函数,训练全部数字的函数
def Neural_Train_0_9(self, alpha=0.2):
for j in range(self.samplenum):
for i in range(10):
y = np.zeros((self.ly_out, 1))
y[i][0] = 1
W2_conv = dlt_c(self.W2, 0) # W2删除第一列并取转置
a1 = self.x[i][j]
a1_en = enlarge_vec(a1) # a1的增广向量,头部加1
r2 = np.dot(self.W1, a1_en.T) # 隐藏层输入向量
a2 = sigmoid_vec(r2) # 隐藏层输出向量
a2_en = enlarge_vec(a2) # a2的增广向量,头部加1
r3 = np.dot(self.W2, a2_en.T) # 输出层输入向量
a3 = sigmoid_vec(r3) # 输出层输出向量
A2 = vec_diag(a2) # 由a2生成对角矩阵
A3 = vec_diag(a3) # 由a3生成对角矩阵
self.Loss.append(abs(np.linalg.norm(y - a3)))
# 反向传递
Delta2 = np.dot(A3 - np.dot(A3, A3), y - a3)
Delta1 = np.dot(A2 - np.dot(A2, A2), W2_conv.T)
Delta1 = np.dot(Delta1, Delta2)
Del_W2 = np.dot(Delta2, a2_en)
Del_W1 = np.dot(Delta1, a1_en)
self.W2 = self.W2 + alpha * Del_W2
self.W1 = self.W1 + alpha * Del_W1
当预测某一张图片时,就用其输出向量中最大的值所在的行数表示其预测结果。根据之前的设定,正好从python计数向量第0行到第9行表示数字1~9,参照前面的函数可以写出预测全部数字的预测函数如下:
# 预测所有数字的正确率
def Neural_Rate_0_9(self):
ra = 0 # 预测正确样本数
rn = 0 # 计算样本总数
for i in range(self.samplenum):
for j in range(10):
rn += 1
a1 = self.x[j][i]
a1_en = enlarge_vec(a1) # a1的增广向量,头部加1
r2 = np.dot(self.W1, a1_en.T) # 隐藏层输入向量
a2 = sigmoid_vec(r2) # 隐藏层输出向量
a2_en = enlarge_vec(a2) # a2的增广向量,头部加1
r3 = np.dot(self.W2, a2_en.T) # 输出层输入向量
a3 = sigmoid_vec(r3) # 输出层输出向量
if np.argmax(a3) == j:
ra += 1
return ra / rn
# 测试单独某张图片预测结果,输出为0~9中的某一个数
def Neural_Predict_0_9(self, x_Pre):
a1 = x_Pre
a1_en = enlarge_vec(a1)
r2 = np.dot(self.W1, a1_en.T)
a2 = sigmoid_vec(r2)
a2_en = enlarge_vec(a2)
r3 = np.dot(self.W2, a2_en.T)
a3 = sigmoid_vec(r3)
return np.argmax(a3)
主程序框架搭建
创建文件main.py写入主程序框架
- 导入库函数
- 调整matplotlib函数中文显示
- 导入数据
数据只需要把上文下载的压缩包直接解压到项目路径即可:
(在“手写”文件夹中,读者也可以自行修改路径并从如下代码中完善:)
from tqdm import tqdm
import matplotlib.pyplot as plt
import random
from NeuralClass import *
# matplotlib画图中中文显示会有问题,需要这两行设置默认字体可以显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
samplenum = int(input('请输入每个数字图片所取的样本数(0~500):')) # 每个数字图片所取的样本数
# x[样本所表示数字的第几个样本][样本表示的数字]
x = [list() for i in range(10)]
print('数据读取中...')
for i in tqdm(range(samplenum)):
for j in range(10):
x[j].append(vector_c(get_gray_mt('手写\\'+str(j)+'\\'+str(j)+'_' + str(i+1) + '.bmp')))
print('读取完成!')
导入数据引入库函数tqdm为数据导入过程添加进度条,导入全部5000个图片数据需要1~2分钟。
生成的三阶张量 x \mathbf{x} x就是训练集,其按次序的两个索引分别为[样本所表示数字的第几个样本] [样本表示的数字]。
需要注意的是,在选择好需要学习的网络对网络进行训练的时候可能将所有样本只从网络中训练一次不能达到很高的正确率,因此需要对网络继续进行训练,调整学习参数,将所有样本再次经过网络…
将神经网络写到主程序中搭建如下框架:
写出代码如下:
while 1:
bool_form = int(input('选择训练全部数字的网络输入”1“,选择训练某个数字的网络输入”0”:'))
if bool_form == 1:
# 构建初始网络
Net1 = Neural_NetWork3(x, 10)
while 1:
alpha = float(input('请输入学习率(建议输入0~1):'))
print('开始训练神经网络...')
Net1.Neural_Train_0_9(alpha)
rate1 = Net1.Neural_Rate_0_9()
print('判断0~9数字正确率为:' + str(round(rate1, 3) * 100) + '%')
bool1 = float(input('是否继续训练?继续请输入1,退出请输入其他数字:'))
if bool1 != 1:
break
plt.figure('损失函数变化图象')
plt.plot(Net1.Loss)
plt.xlabel('迭代次数')
plt.ylabel('损失函数$L =||\\mathbf{y}-\\mathbf{a}_{output}||^{2}$')
plt.show()
while 1:
pre_num1 = int(input('请输入需要预测的图片(用图片上的数字表示):'))
# 从选择的数字中随机抽取一张图片
pre_spnum = random.randint(0, samplenum - 1)
pre_result = Net1.Neural_Predict_0_9(x[pre_num1][pre_spnum])
print('预测结果为:' + str(pre_result))
if pre_result == pre_num1:
print('预测成功!')
else:
print('预测失败!')
img = Image.open('手写\\' + str(pre_num1) + '\\' + str(pre_num1) + '_' + str(pre_spnum + 1) + '.bmp')
img.show()
bool2 = float(input('是否继续预测?继续请输入1,退出请输入其他数字:'))
if bool2 != 1:
break
elif bool_form == 0:
# 构建初始网络
Net2 = Neural_NetWork3(x, 1)
pre_num = int(input('请输入需要预测的数字(0~9):'))
while 1:
alpha = float(input('请输入学习率(建议输入0~1):'))
print('开始训练神经网络...')
Net2.Neural_Train_num(pre_num, alpha)
rate1 = Net2.Neural_Rate_num(pre_num)
print('判断数字' + str(pre_num) + '数字正确率为:' + str(round(rate1, 3) * 100) + '%')
bool1 = float(input('是否继续训练?继续请输入1,退出请输入其他数字:'))
if bool1 != 1:
break
plt.figure('损失函数变化图象')
plt.plot(Net2.Loss)
plt.xlabel('迭代次数')
plt.ylabel('损失函数$L =||\\mathbf{y}-\\mathbf{a}_{output}||^{2}$')
plt.show()
while 1:
pre_num1 = int(input('请输入需要预测的图片(用图片上的数字表示):'))
# 从选择的数字中随机抽取一张图片
pre_spnum = random.randint(0, samplenum - 1)
pre_result = Net2.Neural_Predict_num(x[pre_num1][pre_spnum])
print(pre_result)
if pre_result == True:
print('预测结果为:是' + str(pre_num))
if pre_num1 == pre_num:
print('预测成功!')
else:
print('预测失败!')
else:
print('预测结果为:非' + str(pre_num))
if pre_num1 != pre_num:
print('预测成功!')
else:
print('预测失败!')
img = Image.open('手写\\' + str(pre_num1) + '\\' + str(pre_num1) + '_' + str(pre_spnum + 1) + '.bmp')
img.show()
bool2 = float(input('是否继续预测?继续请输入1,退出请输入其他数字:'))
if bool2 != 1:
break
bool_all = int(input('是否重新选择网络训练?“是”请输入“1”,退出请输入“0”:'))
if bool_all == 0:
break
画图显示时用到了LaTeX编码,网址如下:
https://www.latexlive.com/
执行以上main.py文件过程示例如下:
C:\ProgramData\Anaconda3\python.exe C:/TJUcmj/学科/Python/NeuralNetwork3/Neural_main.py
请输入每个数字图片所取的样本数(0~500):500
数据读取中…
100%|██████████| 500/500 [01:33<00:00, 5.37it/s]
读取完成!
选择训练全部数字的网络输入”1“,选择训练某个数字的网络输入”0”:0
请输入需要预测的数字(0~9):5
请输入学习率(建议输入0~1):0.2
开始训练神经网络…
判断数字5数字正确率为:96.1%
是否继续训练?继续请输入1,退出请输入其他数字:1
请输入学习率(建议输入0~1):0.2
开始训练神经网络…
判断数字5数字正确率为:96.89999999999999%
是否继续训练?继续请输入1,退出请输入其他数字:1
请输入学习率(建议输入0~1):0.5
开始训练神经网络…
判断数字5数字正确率为:97.2%
是否继续训练?继续请输入1,退出请输入其他数字:0
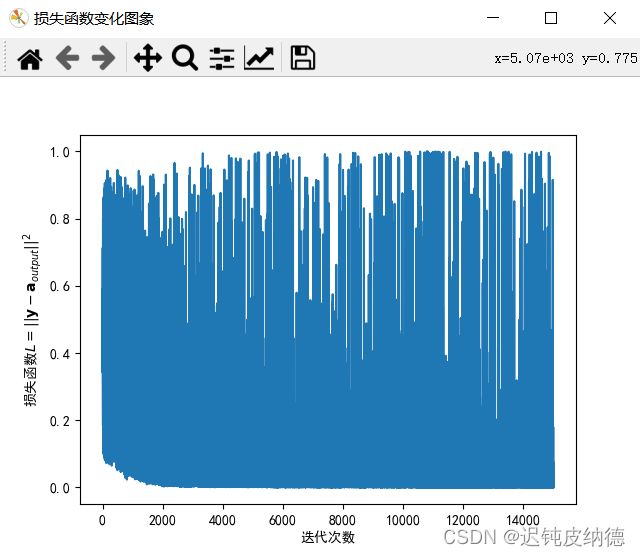
请输入需要预测的图片(用图片上的数字表示):8
[[0.00016551]]
False
预测结果为:非5
预测成功!
![]()
是否继续预测?继续请输入1,退出请输入其他数字:1
请输入需要预测的图片(用图片上的数字表示):5
[[0.0074179]]
False
预测结果为:非5
预测失败!
![]()
是否继续预测?继续请输入1,退出请输入其他数字:1
请输入需要预测的图片(用图片上的数字表示):5
[[0.96203601]]
True
预测结果为:是5
预测成功!
![]()
是否继续预测?继续请输入1,退出请输入其他数字:0
是否重新选择网络训练?“是”请输入“1”,退出请输入“0”:1
选择训练全部数字的网络输入”1“,选择训练某个数字的网络输入”0”:1
请输入学习率(建议输入0~1):0.5
开始训练神经网络…
判断0~9数字正确率为:91.5%
是否继续训练?继续请输入1,退出请输入其他数字:1
请输入学习率(建议输入0~1):0.2
开始训练神经网络…
判断0~9数字正确率为:94.5%
是否继续训练?继续请输入1,退出请输入其他数字:1
请输入学习率(建议输入0~1):0.2
开始训练神经网络…
判断0~9数字正确率为:95.1%
是否继续训练?继续请输入1,退出请输入其他数字:1
请输入学习率(建议输入0~1):0.3
开始训练神经网络…
判断0~9数字正确率为:95.6%
是否继续训练?继续请输入1,退出请输入其他数字:1
请输入学习率(建议输入0~1):0.8
开始训练神经网络…
判断0~9数字正确率为:94.39999999999999%
是否继续训练?继续请输入1,退出请输入其他数字:1
请输入学习率(建议输入0~1):0.1
开始训练神经网络…
判断0~9数字正确率为:96.5%
是否继续训练?继续请输入1,退出请输入其他数字:0
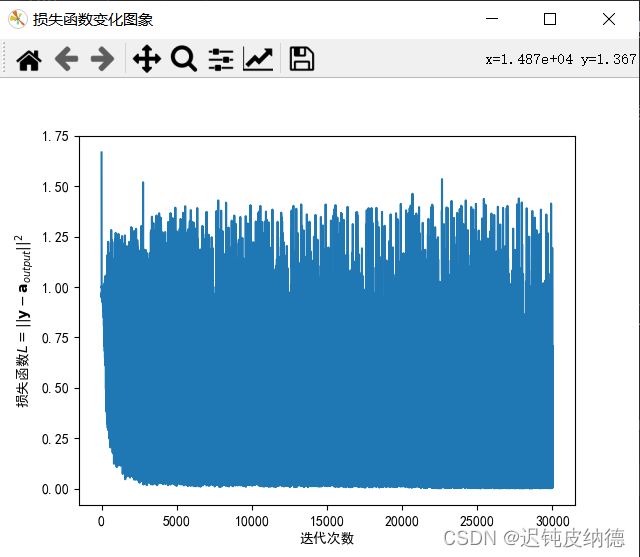
请输入需要预测的图片(用图片上的数字表示):0
预测结果为:0
预测成功!
![]()
是否继续预测?继续请输入1,退出请输入其他数字:1
请输入需要预测的图片(用图片上的数字表示):7
预测结果为:7
预测成功!
![]()
是否继续预测?继续请输入1,退出请输入其他数字:1
请输入需要预测的图片(用图片上的数字表示):4
预测结果为:4
预测成功!
![]()
是否继续预测?继续请输入1,退出请输入其他数字:0
是否重新选择网络训练?“是”请输入“1”,退出请输入“0”:0
进程已结束,退出代码 0
以上是本项目全部内容,自己开发的开源代码供大家学习使用,如有问题请不吝斧正。
本项目存在的问题:在训练某个数字的神经网络时,正样本数和负样本数应该相等,而本项目中为了两个训练网络的连续性,负样本数是正样本数的9倍。因此在训练完整个神经网络之后虽然整体正确率很高,但是在判断本数字时正确率可能比较低。
提供思路如下:
将样本循环训练提出到神经网络类之外在主程序进行,在训练某个数字的神经网络时可以调节负样本的数量。
读者可以自行修改。