机器学习笔记04-梯度下降算法中的学习率(步长)
1、回顾
之前所说的梯度下降算法中有几个细节,求导部分已经在上一节进行说明,接下来主要对公式当中的 α \alpha α,即就是学习率(步长)进行说明。
θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) , f o r ( j = 1 a n d j = 0 ) \theta_{j}:=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J_{\left(\theta_{0}, \theta_{1}\right)},for(j=1 and j=0) θj:=θj−α∂θj∂J(θ0,θ1),for(j=1andj=0)其中 ∂ ∂ θ j J ( θ 0 , θ 1 ) \frac{\partial}{\partial \theta_{j}} J_{\left(\theta_{0}, \theta_{1}\right)} ∂θj∂J(θ0,θ1)其实就是计算的梯度, : = := :=表示赋值, α \alpha α表示学习率(步长)。
梯度下降算法的主要目的是为了求解最优的参数,也就是使得代价函数值最小。假设代价函数为:
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J_{\left(\theta_{0}, \theta_{1}\right)}=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}(x^{(i)})-y^{(i)}\right)^{2} J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
梯度下降算法就是通过不断更新 θ 0 和 θ 1 \theta_{0}和\theta_{1} θ0和θ1的值来达到求取最优的模型,模型表示为:
h θ ( x ) = θ 0 + θ 1 x h_{\theta(x)}=\theta_{0}+\theta_{1} x hθ(x)=θ0+θ1x
2、说明
α \alpha α其实就是就是一个实数,在数学中很好理解。为什么称它为学习率或者步长呢?举个简单的例子:
(1)三个人分别为小孩、青少年和中年,同时要走100m,假设小孩一步走0.5m,青少年一步走1m,中年一步走1.5m(每步都一样),那么谁先到达终点呢?答案肯定是中年,很简单,因为中年一步走的多,所有能更快到达终点,青少年次之,最慢的为小孩。
这就和公式中的 α \alpha α是一样滴,它也是这个用途,用来控制算法每次移动的距离。正常来说, α \alpha α越大,算法每次移动的就越大,越小,每次移动的也就越小。
(2)在之前的例子上再加一条规定,就是必须刚好走100m。计算一下发现,小孩在200步后会恰好走到终点,青少年会在100步后恰好走到终点,而中年会在第67步后走过终点(100.5m),他永远不可能恰好走到100m处。
这也印证了 α \alpha α选值的重要性,理论来说,当 α \alpha α足够小时,总是能得到最优解,但是需要迭代很多次(对应小孩),当 α \alpha α太大时,很容易直接跳过最优值,导致无法收敛(对应中年),只有当选择合适的 α \alpha α时,才能更好更快的收敛(对应青少年)。
总结:当 α \alpha α太小时,可能会需要多次迭代才能收敛,当 α \alpha α太大时,可能导致无法收敛或者会发散,只有选择合适的 α \alpha α时,才能更好的收敛。

3、为什么 α \alpha α太大时会导致无法收敛?
可以自己举个例子带入计算一下,其实就能得到结果。为了方便计算,我以第二节中讲的为基础进行计算。我们的样本为 ( x ( 1 ) , y ( 1 ) ) = ( 1 , 1 ) , ( x ( 2 ) , y ( 2 ) ) = ( 2 , 2 ) , ( x ( 3 ) , y ( 3 ) ) = ( 3 , 3 ) (x^{(1)},y^{(1)})=(1,1),(x^{(2)},y^{(2)}) =(2,2),(x^{(3)},y^{(3)})=(3,3) (x(1),y(1))=(1,1),(x(2),y(2))=(2,2),(x(3),y(3))=(3,3),得到的代价函数如图所示。在此基础上,使用梯度下降算法来求解最优参数。
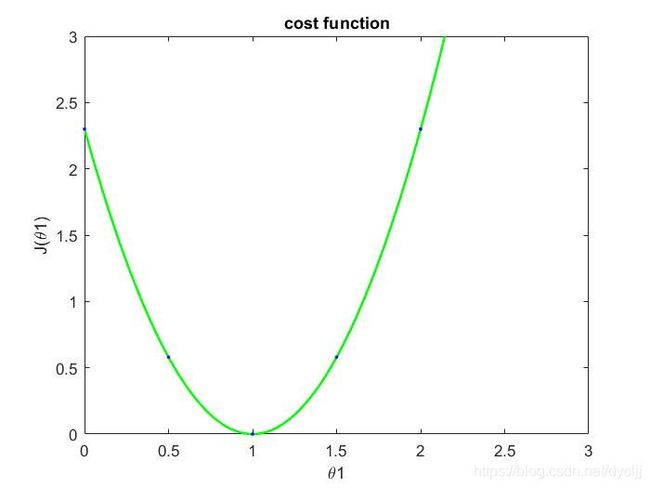
(1)首先,我们都会有一个初始 θ \theta θ值,假设为 θ 0 = 0 , θ 1 = 0 \theta_{0}=0,\theta_{1}=0 θ0=0,θ1=0(此处可以不更新 θ 0 的 值 , 因 为 模 型 为 h θ ( x ) = θ 1 x , θ 0 为 0 \theta_{0}的值,因为模型为h_{\theta(x)}=\theta_{1} x,\theta_{0}为0 θ0的值,因为模型为hθ(x)=θ1x,θ0为0)。
(2)假设 α \alpha α为0.5,更新 θ \theta θ值。
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) \begin{aligned} \theta_{0} &:=\theta_{0}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}(x^{(i)})-y^{(i)}\right) \\ \theta_{1} &:=\theta_{1}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}(x^{(i)})-y^{(i)}\right) \cdot x^{(i)} \end{aligned} θ0θ1:=θ0−αm1i=1∑m(hθ(x(i))−y(i)):=θ1−αm1i=1∑m(hθ(x(i))−y(i))⋅x(i)
当 θ 1 = 0 \theta_{1}=0 θ1=0时,模型为 h θ ( x ) = 0 + 0 ∗ x h_{\theta(x)}=0+0*x hθ(x)=0+0∗x,所以:
h θ ( 1 ) = 0 + 0 ∗ 1 = 0 , h θ ( 2 ) = 0 + 0 ∗ 2 = 0 , h θ ( 3 ) = 0 + 0 ∗ 3 = 0 h_{\theta(1)}=0+0*1 = 0,h_{\theta(2)}=0+0*2 = 0,h_{\theta(3)}=0+0*3 = 0 hθ(1)=0+0∗1=0,hθ(2)=0+0∗2=0,hθ(3)=0+0∗3=0,
①第一次更新:
θ 0 : = 0 − 0.5 ∗ 1 3 ∗ [ ( 0 − 1 ) + ( 0 − 2 ) + ( 0 − 3 ) ] = 1 \theta_{0} := 0 -0.5*\frac{1}{3}*[(0-1)+(0-2)+(0-3)]=1 θ0:=0−0.5∗31∗[(0−1)+(0−2)+(0−3)]=1
θ 1 : = 0 − 0.5 ∗ 1 3 ∗ [ ( 0 − 1 ) ∗ 1 + ( 0 − 2 ) ∗ 2 + ( 0 − 3 ) ∗ 3 ] = 7 3 \theta_{1} := 0 -0.5*\frac{1}{3}*[(0-1)*1+(0-2)*2+(0-3)*3]= \frac{7}{3} θ1:=0−0.5∗31∗[(0−1)∗1+(0−2)∗2+(0−3)∗3]=37
可以看出, θ 1 \theta_{1} θ1的值直接从0到了2.3,跳过了最低点。
②第二更新:此时模型为 h θ ( x ) = 1 + 7 3 x \begin{array}{l}h_{\theta(x)}=1+ \frac{7}{3}x \end{array} hθ(x)=1+37x
θ 0 : = 1 − 0.5 ∗ 1 3 ∗ [ ( 10 3 − 1 ) + ( 17 3 − 2 ) + ( 8 − 3 ) ] = − 5 6 \theta_{0} := 1 -0.5*\frac{1}{3}*[(\frac{10}{3}-1)+(\frac{17}{3}-2)+(8-3)]=-\frac{5}{6} θ0:=1−0.5∗31∗[(310−1)+(317−2)+(8−3)]=−65
θ 1 : = 7 3 − 0.5 ∗ 1 3 ∗ [ ( 10 3 − 1 ) ∗ 1 + ( 17 3 − 2 ) ∗ 2 + ( 8 − 3 ) ∗ 3 ] = − 16 9 \theta_{1} := \frac{7}{3}-0.5*\frac{1}{3}*[(\frac{10}{3}-1)*1+(\frac{17}{3}-2)*2+(8-3)*3]=- \frac{16}{9} θ1:=37−0.5∗31∗[(310−1)∗1+(317−2)∗2+(8−3)∗3]=−916
可以看出, θ 1 \theta_{1} θ1的值又直接从2.3到了-1.8。
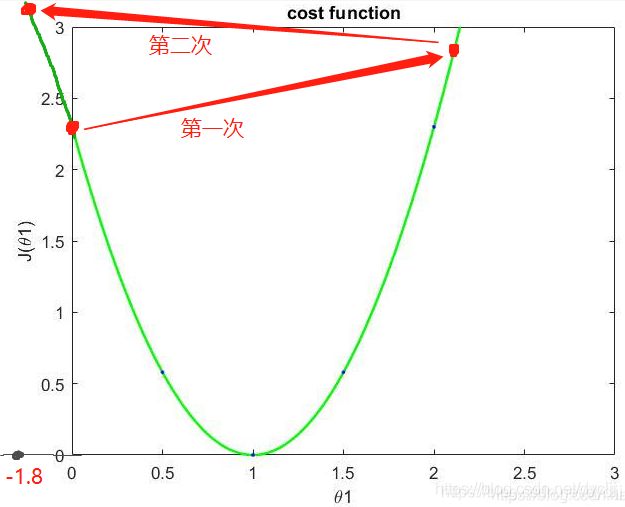
所以说,当 α \alpha α值较大时,将会导致无法收敛,或者会导致发散。
推荐的学习率值:
