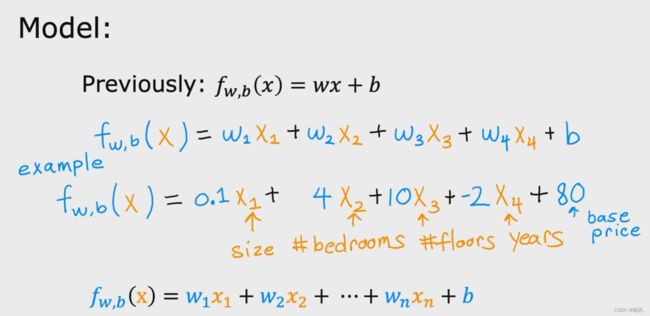【机器学习】多元特征线性回归与向量化
系列文章目录
第六章 Python 机器学习入门之多元特征线性回归与向量化
目录
系列文章目录
文章目录
一、什么是多类特征
二、向量化
三 、多元线性回归的梯度下降法
总结
一、什么是多类特征
顾名思义,多类特征就是指有多个特征值,回想一下我们前面学习的线性回归模型,其中只有一个特征w, 它是房子的大小。
但是我们在实际预测价格的时候,使用一个特征可能预测的并不会很准。因为价格不仅仅是跟房子的大小有关,像房子的年份,有多少房间等等,都会影响到房子的价格。所以这些都可以作为特征值,这样一来,就有了多类特征了。
有了多类特征值,会使线性回归学习的更快,更强大,因为它不仅着眼于一个特征。下面来具体看看。

在线性回归的原始版本中,我们有一个房子大小的特征x,并且可以预测房子的价格y ,所以线性回归模型就是f(x) = w * x + b
但是现在,我们不仅有房子的大小作为预测价格的特征,而且还有卧室的数量,楼层的数量和房子的年代,这会给我们更多的信息来预测价格
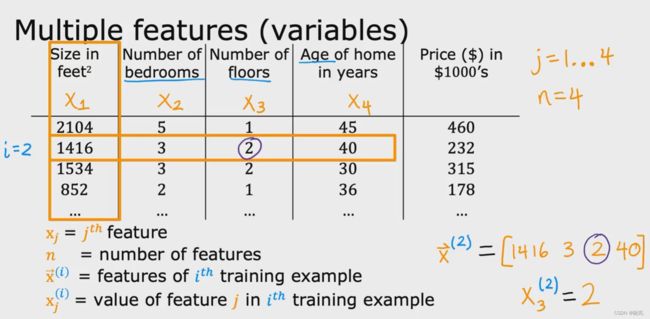
我们可以使用x1, x2, x3, x4 来表示这些特征,如果引入更多符号,就使用x_j 或 xj 来表示特征列表,
这里的j 就是从1到4,一般使用n 表示特征的数量,用x 上标 i 来表示第 i 个训练的例子,
比如x 上标2 ,就表示第二个训练例子的特征向量, 它是一个向量的数字列表,
x 上标2下标3,表示第二个训练例子的特征向量中的第三个特征的值,它是一个具体的数
之前我们是这样定义模型的,x 是一个单一的特征,所以是一个数字
但是现在我们有了多个特征,我们将使用不同的方式定义它,
现在,模型将写成 f(x) = w1*x1 + w2*x2 + w3*x3 + w4*x4 + b
将w 写成向量的数字列表,将x 也写成向量模式,这样就可以简化模型了,如图,可以直接使用点乘,很简单的就写出了模型。
使用点向量表示法 可以让我们用更少的字符写出更加紧凑的模型,
这种类型的线性回归,具有多种改进特征的模型 被称为多元线性回归模型,与一元线性回归不同,一元线性回归只有一个特征
注意,这个模型被称为多元特征线性回归,也叫多元线性回归,而不是线性回归,线性回归指的是其它的东西
二、向量化
向量化 vectorization
在我们实现学习算法时,使用矢量化可以使我们的代码更短,也可以使其运行的速率更高
学习如何编写矢量化代码,将使我们可以利用现代数值线性代数库,甚至可以代表图形处理单元的GPU 硬件,这是客观设计用于加速计算机中的计算机图形的硬件
但是事实证明,可以在我们编写矢量化代码时使用,以帮助我们更快的执行代码
下面,来举例说明向量化的含义:
参数和特征 parameters and features
这是一个带有参数w 和 b 的示例,其中w 是一个包含3个数字的向量,x 是一个包含3个数字的特征向量,这里n = 3
注意,在线性代数中,索引或计数都是从1开始的,因此第一个值的下标为w1 和 x1,
在Python代码中,我们可以使用这样的数组定义这些变量w,b和x,
在这里,使用了Python中的一个名为NumPy 的数值线性代数库,它是迄今为止Python 和机器学习中使用最广泛的数值线性代数库了,
因为在Python中,在数组中计数时 数组的索引 都是从0开始的,我们将使用w[0] 访问w 的第一个值,使用w[1] 访问w 的第二个值...
包括Python在内的许多编程语言都是从0而不是1开始计数的
下面,我们来看看没有矢量化的模型 如何来实现计算模型的预测,
可以看见我们需要将每个参数都乘以它的相关特征,这样写很繁琐,这只是 n = 3 时的代码,如果n = 300呢,所以这样写代码时非常低效的。
如果不使用矢量化,我们还有另一种方法,使用for循环,在数学中,我们可以求和运算符,将w_j 和 x_j 的所有乘积相加,j从1 到 n, 再加上b
注意,range(0,n) 表示范围是从0到 n-1,并不包括n , 也可以直接写range(n) ,
虽然这个实现比第一个好一点,但是仍然没有使用分解,效率还不够高,
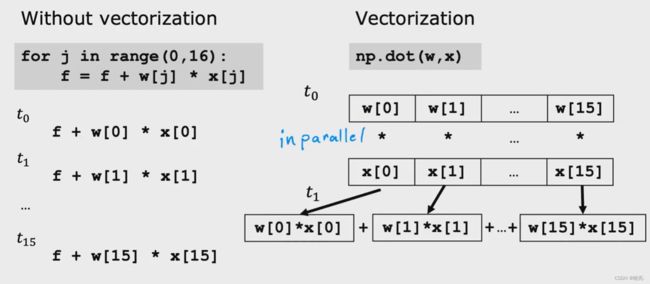
现在让我们来看看如何使用矢量化来做到这一点,只需要一行代码就可以实现它,dot 是点函数
这个NumPy 点函数是两个向量之间的点积运算的向量化实现,尤其是当n 很大时,只要dot函数运行速度都比前面两个方法都快很多,
我们可以发现,使用矢量化会使得我们的代码更短,而且运行速度更快。
矢量化实现更快的原因是在幕后,NumPy dot 函数能够在我们的计算机中使用并行硬件。
使用矢量化,NumPy dot 函在计算机中使用并行硬件,它可以将每对w 和 x 同时并行相乘,然后计算机将这16个数字使用专门的硬件,
可以非常有效的将题目相加,而不需要一个一个的相加。这意味着使用向量化的代码执行计算时间比不使用向量化的代码要短得多。
下面,来看一个具体的例子,它是如何帮助实现多元特征线性回归的,也就是具有多个特征的线性回归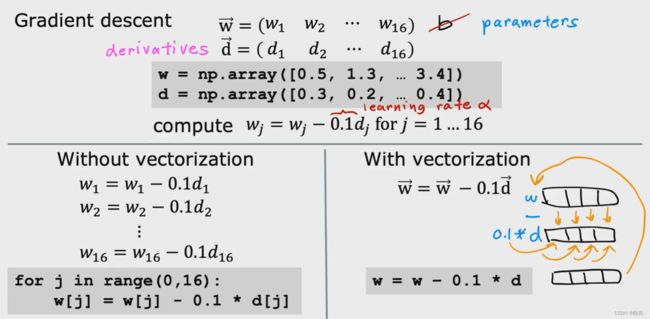
假设我们有16个特征和16个参数的问题 从w1 到 w16,除了参数b, 我们计算了16个权重的16个导数项,
在这个例子中,我们将忽略参数b ,学习速率α 取0.1,
采用for 循环也是一步步的更新,使用矢量化化,它不用一个一个的乘,它取向量w 中的所有的16个值 并行减去0.1乘以向量d 中的所有16个值,并将计算出来的16个结果返回给w
所有的这些都是在同一时间,同一步骤中完成的。
例子中只有16个特征,运行速度可能相差不大,但是有成千上万个特征时,向量化实现程序的速度将会比for 循环实现要快得多。
三 、多元线性回归的梯度下降法
多元线性回归的梯度下降法 gradient descent for multiple regression
我们已经学习了梯度下降,多元线性回归和矢量化,把这些放在一起,我们就可以实现梯度下降的多元线性回归与矢量化。
使用向量表现法来简洁的写出多元线性回归
我们有参数 w1 到 wn ,还有b 。 w1 到 wn并不是单独的数字,而是单独的参数
把所有的w 集合写成向量w ,n 为 向量w 的长度,
我们把这个模型想象成一个向量w 和 b ,b 是一个数字,
在此之前我们要找到多元线性回归,然后使用向量表示法,来简化它,我们可以把这个模型写成 向量w 与向量x 的 点乘 + b
代价函数可以定义为 j( w1, ..... wn ,b),但是不要把 j 看成是这些n 个不同参数的函数,如图,这个写法也可以使用向量简化
让我们来看看实现梯度下降时会是什么样子,我们来看一下导数项
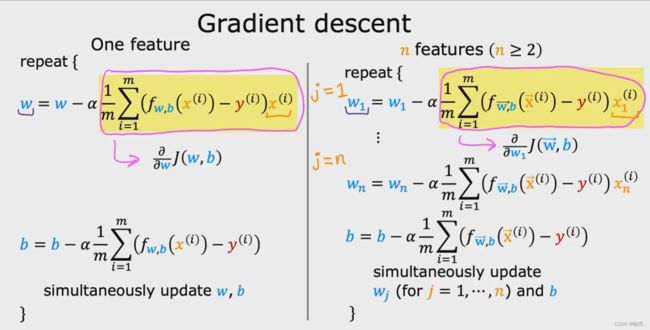
我们会看到梯度下降在多个特征中变得有点不同,而不是一个特征,
当我们只有一个特征时,如图左边 one feature ,我们对w 有一个更新的公式,对b有一个单独的更新公式,
当我们只有n个特征时,如图右边,与一个特征时计算相似
an alternative gradient descent 另一种梯度下降的方法
关于线性回归的w 和 b 的另一种方法
这个方法叫做 normal equation 正规方程,梯度下降时使代价函数最小化的一个很好的方法,来找到 w 和 b,
具体的可以参考一下下面的博文:
(45条消息) 梯度下降与正规方程_QEcode的博客-CSDN博客_正规方程和梯度下降
这一种算法只适用于线性回归,它并不需要进行迭代梯度下降
事实证明,使用高级线性代数库来一次求解w 和 b 是可能的,而不需要迭代,
算法的 disadvantages 缺点
不像梯度下降,正规方程不能推广到其他学习算法,比如回归算法和神经网络等其他的算法,
正规方程运行的也很慢,如果特征 n 的数量很大时,运行会很慢,
总结
只有一个特征变量的线性模型叫做一元线性回归模型,
含有多个特征变量的线性模型叫做多元特征线性回归模型,也叫做多元线性回归模型,而不是线性回归,线性回归指的是其它的东西
对于多元线性回归模型,我们在实现代码时,使用矢量化可以使我们的代码更短,也可以使其运行的速率更高
多元线性回归模型求代价函数的最小值有两个方法,一个是梯度下降算法,另一个方法叫 normal equation 正规方程
正规方程虽然可以找到多元线性回归模型代价函数的最小值,但是有不少缺点
1. 不像梯度下降,正规方程不能推广到其他学习算法,比如回归算法和神经网络等其他的算法,只适用于线性回归,它并不需要进行迭代梯度下降
2.正规方程运行的很慢,如果特征 n 的数量很大时,运行会很慢