MASS | 广义线性模型(四)——负二项回归
本篇是“广义线性模型”系列推文的最后一篇,来介绍另外一种重要的广义线性模型:负二项回归。
同泊松回归一样,负二项回归也是计数模型。由于泊松回归的内在要求是因变量的数学期望和方差相等,而当数据序列出现“过度离散”(方差比理论值大)时,可有两种方式进行模型修正:
使用准泊松分布族;
改用负二项回归。
前者已经介绍过了,本篇来介绍后者——负二项回归。
模型形式
负二项回归的模型形式与泊松回归十分相似。
泊松回归:
负二项回归:
泊松分布与负二项分布有着内在的联系。当泊松分布的参数 不再是一个确定的数值,而是服从伽马分布进行变化时,此时的分布形式称为伽马-泊松混合分布,负二项分布是伽马-泊松混合分布的特例。
《Modern Applied Statistics with S-PLUS》[1]上有关于负二项分布与泊松分布关系的描述:
负二项分布的方差恒大于数学期望,并受参数 的影响。从模型形式上看,负二项回归比泊松回归多了一个随机项 :
为伽马分布的记号。
负二项分布
泊松分布的概率函数如下:
伽马分布 的概率密度函数如下:
为形状参数, 为逆尺度参数。数学期望 ,方差 。
伽马-泊松混合分布的概率密度函数如下:
负二项分布的概率函数如下:
对比伽马-泊松混合分布和负二项分布的概率(密度)函数,令 , ,则二者相等。
负二项分布的意义:随机事件刚好第 次发生(不发生)时所经历的不发生(发生)的次数。
模型的R代码
负二项回归虽然属于广义线性模型,但在stats工具包中并没有定义负二项分布族函数。
MASS工具包的glm.nb函数可以进行负二项回归,并自动确定 参数的取值。
glm.nb(formula, data, weights,
subset, na.action,
start = NULL, etastart, mustart,
control = glm.control(...),
method = "glm.fit",
model = TRUE, x = FALSE, y = TRUE,
contrasts = NULL, ...,
init.theta, link = log)
MASS工具包的名称即上面提到的《Modern Applied Statistics with S-PLUS》的首字母缩写;
glm.nb函数专门用于负二项回归,因此无需family参数。
library(MASS)
model.nb <- glm.nb(Days ~ Eth + Sex + Age+ Lrn,
data = quine)
summary(model.nb)
##
## Call:
## glm.nb(formula = Days ~ Eth + Sex + Age + Lrn, data = quine,
## init.theta = 1.274892646, link = log)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.7918 -0.8892 -0.2778 0.3797 2.1949
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.89458 0.22842 12.672 < 2e-16 ***
## EthN -0.56937 0.15333 -3.713 0.000205 ***
## SexM 0.08232 0.15992 0.515 0.606710
## AgeF1 -0.44843 0.23975 -1.870 0.061425 .
## AgeF2 0.08808 0.23619 0.373 0.709211
## AgeF3 0.35690 0.24832 1.437 0.150651
## LrnSL 0.29211 0.18647 1.566 0.117236
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for Negative Binomial(1.2749) family taken to be 1)
##
## Null deviance: 195.29 on 145 degrees of freedom
## Residual deviance: 167.95 on 139 degrees of freedom
## AIC: 1109.2
##
## Number of Fisher Scoring iterations: 1
##
##
## Theta: 1.275
## Std. Err.: 0.161
##
## 2 x log-likelihood: -1093.151
MASS工具包还定义可以在glm函数中使用的负二项分布族函数negative.binomial:
negative.binomial(theta = stop("'theta' must be specified"),
link = "log")
使用negative.binomial函数时需指定 参数。根据《Modern Applied Statistics with S-PLUS》中的方法,可以使用MASS工具包中的logtrans函数大致确定 的取值:
logtrans(Days ~ Eth + Sex + Age+ Lrn,
data = quine)
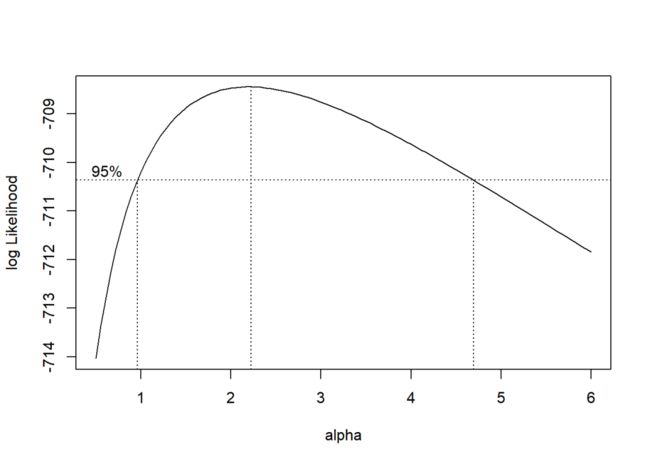
根据上图, 的最佳取值约等于2。
model.nb2 <- glm(Days ~ Eth + Sex + Age+ Lrn,
family = negative.binomial(2),
data = quine)
summary(model.nb2)
##
## Call:
## glm(formula = Days ~ Eth + Sex + Age + Lrn, family = negative.binomial(2),
## data = quine)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.2421 -1.0864 -0.3369 0.4767 2.7006
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.88658 0.22715 12.708 < 2e-16 ***
## EthN -0.56765 0.15245 -3.724 0.000285 ***
## SexM 0.08699 0.15903 0.547 0.585268
## AgeF1 -0.44501 0.23909 -1.861 0.064820 .
## AgeF2 0.09283 0.23451 0.396 0.692819
## AgeF3 0.35938 0.24659 1.457 0.147260
## LrnSL 0.29671 0.18594 1.596 0.112812
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for Negative Binomial(2) family taken to be 1.483669)
##
## Null deviance: 280.18 on 145 degrees of freedom
## Residual deviance: 239.11 on 139 degrees of freedom
## AIC: 1120.5
##
## Number of Fisher Scoring iterations: 7
相关阅读:
stats | 概率分布与随机数生成(一)——离散型分布
stats | 广义线性模型(二)——泊松回归
参考资料
[1]
Venables, W. N. and Ripley, B. D. (1999) Modern Applied Statistics with S-PLUS. Third Edition. Springer .
