MATLAB Appdesigner实用技巧（四）：在APP坐标区实时观察模型姿态信息

1.四元数（或角度）显示姿态

在此项目中，笔者需要实时观测到设备的姿态信息。在学习了旋转相关的数学知识后，我决定采用四元数来实现姿态显示。当然读者也可以基于欧拉表示法来编写代码实现该功能，不过要重点考虑一下在项目的使用场景中是否存在奇异值，防止欧拉表示法定义所导致的万向结死锁现象。关于旋转的数学原理，我推荐读者阅读大神Krasjet*的文章。相关资料和参考文献均在他的Github网站上：GitHub - Krasjet/quaternion: A brief introduction to the quaternions and its applications in 3D geometry.，读者可自行学习。对于四元数的可视化理解，推荐读者观看B站用户3Blue1Brow的视频讲解：四元数的可视化_哔哩哔哩_bilibili，相当详细、直观，便于理解。原理性的东西笔者在此不再阐述，仅介绍如何基于四元数在MATLAB App中实现模型姿态的实时显示。

在此处，我使用.m文件来阐述如何完整地跑通整个流程，然后讲解如何将其移植入App。

我们需要准备一组角度数据（或者四元数数据，笔者当初的程序只保存了角度数据）和模型的.mat文件。.mat文件中以元胞数组的形式存储Patch类型的“Faces”属性和“Vertices”属性。

1.1 打开Excel文件和.mat文件并绘制模型

1.首先我们需要将存储角度数据的Excel文件和存储模型数据的.mat文件打开，并利用模型文件中的数据将模型的初始位置绘制出来。在脚本中输入如下代码：

clc; clear; close all

%%
[filename,pathname] = uigetfile("*.xlsx"); % 使用Windows的文件管理器获得Excel文件的路径和文件名
Matrix = readmatrix([pathname,filename]); % 打开Excel文件并将表格转化为double矩阵
[modelfile,modelpath] = uigetfile("*.mat"); % 同理，使用文件资源管理器获取模型.mat文件的路径和文件名
%%
model = load([modelpath,modelfile]); % 打开模型文件。这里强烈推荐读者使用load函数，因为open函数在App打包成.exe文件后不可用
%%
F = model.modelData{2}; % .mat文件中存储的模型Faces属性
V = model.modelData{1}; % .mat文件中存储的模型Vertices属性
f = figure(1);
p = patch("Faces",F,"Vertices",V); % 使用patch绘制模型
view(3); % 将坐标区视角设置为三维视角
set(p,"FaceColor",[1 0 0]); % 设置模型面的颜色
set(gca,"XLim",[-1 1],"YLim",[-1 1],"ZLim",[-1 1]) % 指定三个坐标轴的显示范围

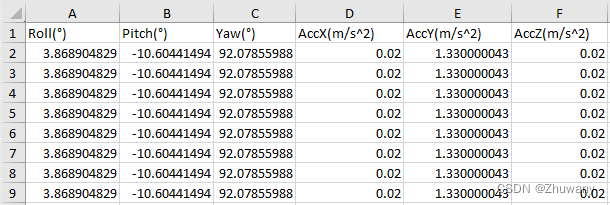
2.笔者保存的数据格式为Roll、Pitch、Yaw并列，如下图所示：

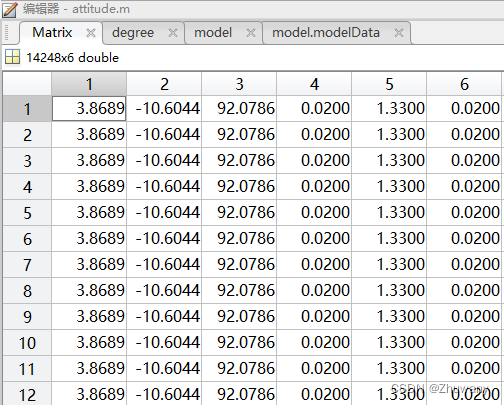
使用“readmatrix”函数打开后，“Matrix”变量的数据类型如下：

可以看到，该函数隐去了第一行的文字，只显示数字信息。并且该变量的类型是double类型，也就是说，我们可以直接对这个矩阵进行操作。

3.在MATLAB Appdesigner实用技巧（一）：在App的坐标区显示自己建模的三维模型，笔者已经详细叙述了如何保存模型的数据用于在坐标区绘制三维模型，这里不再赘述。但是要重复说明一点：使用load函数打开.mat文件后，上文代码中的model变量是一个struct类型的变量：

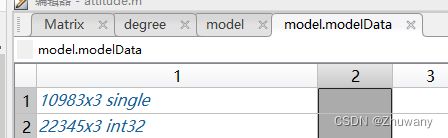
因此调用时要使用“.”来调用。“modelData”是struct变量“model”的一个属性，它是一个元胞数组，两个元胞分别存储了模型的Faces和Vertices数据：

上图为Patch变量的属性列表。可见，其中single类型为Vertices数据，int32类型为Faces数据。为简化代码起见，我使用“F”、“V”来分别存储这两个数据：

F = model.modelData{2}; % .mat文件中存储的模型Faces属性
V = model.modelData{1}; % .mat文件中存储的模型Vertices属性

4.得到上面两个属性后，就可以使用patch函数绘制模型了。

f = figure(1);
p = patch("Faces",F,"Vertices",V); % 使用patch绘制模型
view(3); % 将坐标区视角设置为三维视角
set(p,"FaceColor",[1 0 0]); % 设置模型面的颜色
set(gca,"XLim",[-1 1],"YLim",[-1 1],"ZLim",[-1 1]) % 指定三个坐标轴的显示范围

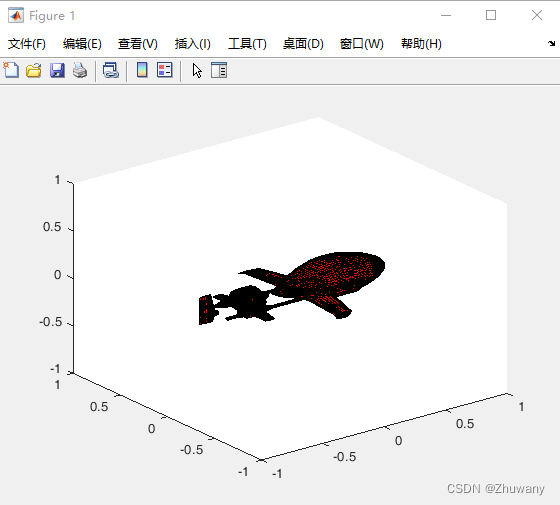
至此，打开文件并绘制模型这一步，我们就完成了。运行上述代码，效果如下：

1.2 将角度转化为四元数，再转化为旋转矩阵

在上一节，我们通过“readmatrix”函数读取Excel文件得到了double类型的矩阵。

其中前三列为Roll（X）、Pitch（Y）、Yaw（Z）角，旋转顺序为“ZYX”，且为角度制。

1.首先我们将前三列数据提取并保存起来：

degree = Matrix(:,1:3)/180*pi;

这里我们需要将角度变为弧度制，然后再转化为四元数。（因为接收到下位机的四元数数据后，quat2angle函数转化来的三个角度值均为弧度制，而保存时我将其改为了角度制）

2.将“degree”变量的每一行转化为四元数，然后转化为旋转矩阵（以第一行为例）：

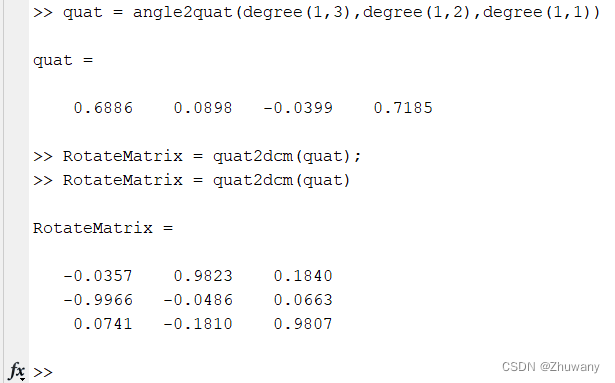
quat = angle2quat(degree(1,3),degree(1,2),degree(1,1)); % Z(Yaw) Y(Pitch) X(Roll)
RotateMatrix = quat2dcm(quat);

运行上述代码，结果如下：

我们就得到了相应的旋转矩阵。

注意：angle2quat函数实际上可以输入四个参数，第四个参数是旋转顺序，默认为“ZYX”。如果读者使用了其他的旋转顺序，则需要输入旋转顺序，语法如下：

quat = angle2quat(degree(1,3),degree(1,1),degree(1,2),"ZXY");

再注意**：angle2quat函数中前三个角度值的顺序一定要和最后一个输入参数，也就是旋转顺序相同。以本项目为例，Yaw为Z轴，Pitch为Y轴，Roll为X轴，旋转顺序为ZYX。则在将角度转化为四元数时，在函数angle2quat中输入角度的顺序也必须是Z$\to$Y$\to$X。这是由该系列函数的语法决定的。读者可以在命令行中输入如下指令：

help quat2angle

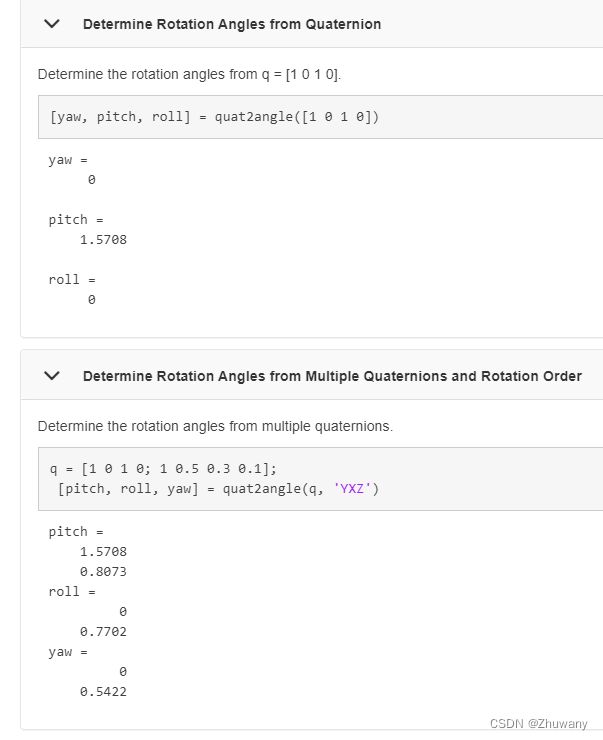
打开函数的帮助文档，找到如下示例：

可以看到，输出的角度的顺序和指定的旋转顺序是一一对应的。第一个示例中，旋转顺序是默认的“ZYX”

1.3 更新模型位置信息

1.得到旋转矩阵后，我们就可以将旋转矩阵与Vertices矩阵右乘，得到新的位置信息。然后，使用set函数将新的Vertices赋给Patch句柄：

newV = V*RotateMatrix;
set(p,"Vertices",newV);

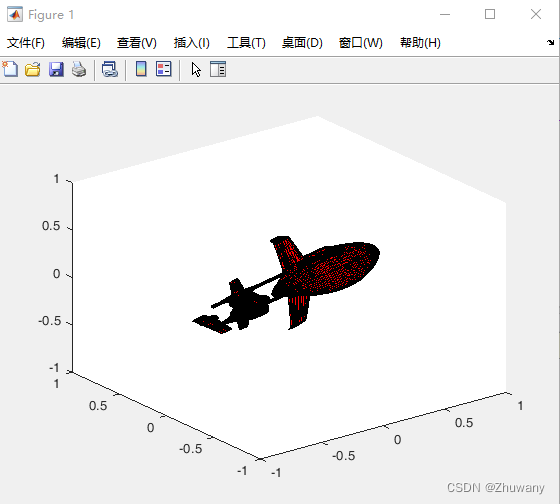
运行上述代码，结果如下：

可以看到，与初始位置相比，模型的姿态发生了变化。至此，我们就可以根据角度数据，实时观看模型的姿态信息了。

2.将所有的数据连续进行上述过程。在笔者的下位机程序中，回传频率设置的为50Hz，即0.02s一帧数据。所以使用表格数据测试时，要设置延时0.02s。代码如下：

for i = 1:length(degree)
    quat = angle2quat(degree(i,3),degree(i,2),degree(i,1));
    RotateMatrix = quat2dcm(quat);
    newV = V*RotateMatrix;
    set(p,"Vertices",newV);
    pause(0.02);
end

运行代码，效果如下。可以看到模型的姿态在持续变化。

至此，整个流程我们就走通了。完整代码（上面的各小节是将该代码拆开讲解，若有不理解的地方可回看上面的分节讲解。此处为方便读者直接移植，重新贴一遍完整代码）：

clc; clear; close all

%%
[filename,pathname] = uigetfile("*.xlsx");
Matrix = readmatrix([pathname,filename]);
[modelfile,modelpath] = uigetfile("*.mat");
%%
f = figure(1);
model = load([modelpath,modelfile]);
%
F = model.modelData{2};
V = model.modelData{1};
p = patch("Faces",F,"Vertices",V);
view(3);
set(p,"FaceColor",[1 0 0]);
set(gca,"XLim",[-1 1],"YLim",[-1 1],"ZLim",[-1 1])
%%
degree = Matrix(:,1:3)/180*pi;

for i = 1:length(degree)
    quat = angle2quat(degree(i,3),degree(i,2),degree(i,1));
    RotateMatrix = quat2dcm(quat);
    newV = V*RotateMatrix;
    set(p,"Vertices",newV);
    pause(0.02);
end

1.4 在App中实现上述功能

功能实现方法介绍完毕，现在我们需要该功能移植到appdesigner中。

我们使用按钮控件来实现上述功能。注意，该例子仅适用于已经有成型的角度数据的情况。如果读者接入了下位机，则需要将代码写入通信组件的回调函数中。关于这方面，可以参考MATLAB Appdesigner开发独立桌面App全流程（一）：以打开串口功能为例介绍Appdesigner的基本使用、MATLAB Appdesigner实用技巧（二）：MATLAB App建立TCP服务端和下位机通信、MATLAB Appdesigner实用技巧（三）：在App中实现示波器效果/动态波形效果的相关内容。

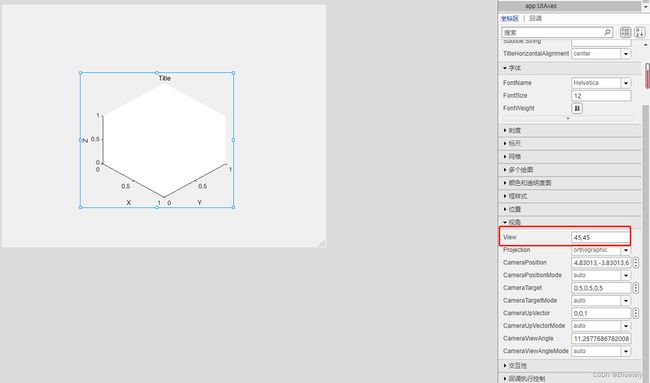
1.新建坐标区并调整视角为[45,45]，将其变为三维显示的坐标区。将其命名为“ModelUIAxes”

2.新建按钮并添加回调函数。将其命名为“run”。

3.转到代码视图，将1.3节中的代码移植到按钮回调函数中，但是有几个位置需要做修改。修改的地方我在下面代码的注释当中进行解释。

% Button pushed function: runButton
function runButtonPushed(app, event)
   	%%
	[filename,pathname] = uigetfile("*.xlsx");
   	Matrix = readmatrix([pathname,filename]);
   	[modelfile,modelpath] = uigetfile("*.mat");
   	%%
   	%%% 此处的f = figure(1)已删除，否则会和软件图窗冲突
  	model = load([modelpath,modelfile]);
   	%
  	F = model.modelData{2};
    V = model.modelData{1};
    %%% 绘制模型时，要指定模型绘制的坐标区
   	p = patch(app.ModelUIAxes,"Faces",F,"Vertices",V);
   	%%% 此处的view(3)要删除，否则会多出来一个figure
   	set(p,"FaceColor",[1 0 0]);
   	%%% 此时我们不再需要在代码中指定坐标区的显示范围，直接在设计视图中修改控件属性即可。
   	%%
 	degree = Matrix(:,1:3)/180*pi;

   	for i = 1:length(degree)
 		quat = angle2quat(degree(i,3),degree(i,2),degree(i,1));
   		RotateMatrix = quat2dcm(quat);
    	newV = V*RotateMatrix;
       	set(p,"Vertices",newV);
     	pause(0.02);
   	end
end

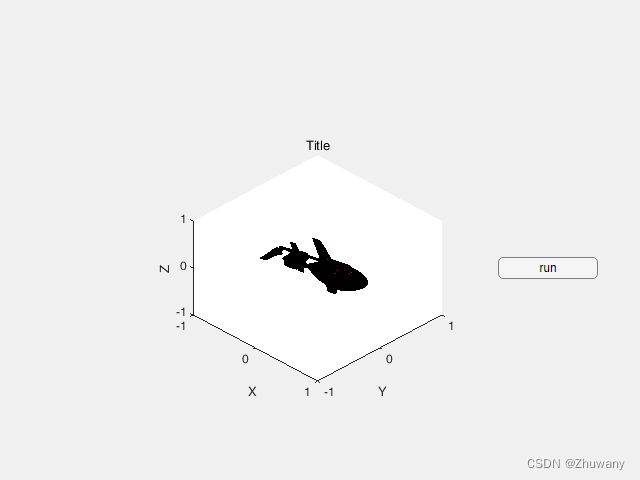
4.运行App，效果如下：

至此，我们就完成了在App中实现了姿态显示的功能。