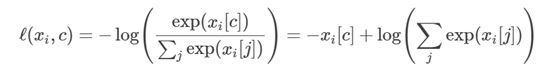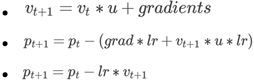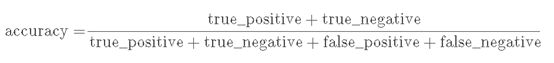使用LeNet实现图像分类任务

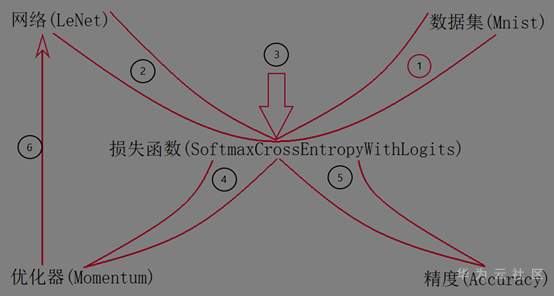
本篇的主要内容是解析一下使用MindSpore深度学习框架训练LeNet网络对Mnist数据集进行分类。首先我给大家展示出本篇内容的一个示意图，帮助大家更直观的看到训练过程的一个重要步骤，如图所示，其中1、2、3…表示训练过程中的次序，下面我们也将从这些次序进行解析。

训练导图

1. 数据集(Mnist)

Mnist数据集来自美国国家标准与技术研究所, National Institute of Standards and Technology (NIST). 训练集 (training set) 由来自 250 个不同人手写的数字构成，其中 50% 是高中学生，50% 来自人口普查局（the Census Bureau）的工作人员，测试集（test set）也是同样比例的手写数字数据。

• Mnist数据集结构

它包含了以下四个部分，数据集中，训练样本：共60000个，其中55000个用于训练，另外5000个用于验证。测试样本：共10000个，验证数据比例相同。MNIST数据集下载页面：http://yann.lecun.com/exdb/mnist/。

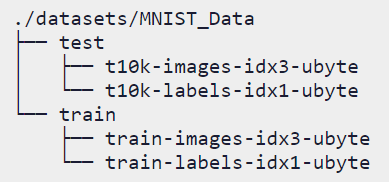
请按照图1中位置的关系进行存放。

图1：数据集结构图

• Training set images: train-images-idx3-ubyte.gz (9.9 MB, 解压后 47 MB, 包含 60,000 个样本)
• Training set labels: train-labels-idx1-ubyte.gz (29 KB, 解压后 60 KB, 包含 60,000 个标签)
• Test set images: t10k-images-idx3-ubyte.gz (1.6 MB, 解压后 7.8 MB,包含 10,000 个样本)
• Test set labels: t10k-labels-idx1-ubyte.gz (5KB, 解压后 10 KB, 包含 10,000 个标签)

MNIST 数据集已经成为一个“典范”，很多教程都会选择从它下手。本次我们使用MindSpore深度学习框架进行加载。

• 检查数据集

在我们将Mnist数据集下载存放好之后，我们需要检查一下数据集的完整性和质量，使用MindSpore深度学习框架撸它，上代码：

1.   import matplotlib.pyplot as plt  

2.   import matplotlib  

3.   import numpy as np  

4.   import mindspore.dataset as ds  

5.     

6.   train_data_path = "./datasets/MNIST_Data/train"  

7.   test_data_path = "./datasets/MNIST_Data/test"  

8.   mnist_ds = ds.MnistDataset(train_data_path)  

9.   print('The type of mnist_ds:', type(mnist_ds))  

10.  print("Number of pictures contained in the mnist_ds：", mnist_ds.get_dataset_size())  

11.    

12.  dic_ds = mnist_ds.create_dict_iterator()  

13.  item = next(dic_ds)  

14.  img = item["image"].asnumpy()  

15.  label = item["label"].asnumpy()  

16.    

17.  print("The item of mnist_ds:", item.keys())  

18.  print("Tensor of image in item:", img.shape)  

19.  print("The label of item:", label)  

20.    

21.  plt.imshow(np.squeeze(img))  

22.  plt.title("number:%s"% item["label"].asnumpy())  

23.  plt.show()  

• 数据增强

以上我们检查了数据集的正确性，但是想要这样使用还是不行的，我们还需要将数据集处理成可以喂入网络模型的规格，该过程也可以称为数据预处理，对应于训练导图中的步骤1。

这里还可以再详细的分为：读入数据集；定义操作并作用到数据集；进行shuffle、batch操作。我们使用MindSpore深度学习框架撸它，上代码：

1.   #首先导入MindSpore中mindspore.dataset和其他相应的模块。  

2.   import mindspore.dataset as ds  

3.   import mindspore.dataset.transforms.c_transforms as C  

4.   import mindspore.dataset.vision.c_transforms as CV  

5.   from mindspore.dataset.vision import Inter  

6.   from mindspore import dtype as mstype  

7.     

8.     

9.   #定义预处理操作  

10.  def create_dataset(data_path, batch_size=32, repeat_size=1,  

11.                     num_parallel_workers=1):  

12.      # 定义数据集  

13.      mnist_ds = ds.MnistDataset(data_path)  

14.      resize_height, resize_width = 32, 32  

15.      rescale = 1.0 / 255.0  

16.      shift = 0.0  

17.      rescale_nml = 1 / 0.3081  

18.      shift_nml = -1 * 0.1307 / 0.3081  

19.    

20.      # 定义所需要操作的map映射  

21.      resize_op = CV.Resize((resize_height, resize_width), interpolation=Inter.LINEAR)  

22.      rescale_nml_op = CV.Rescale(rescale_nml, shift_nml)  

23.      rescale_op = CV.Rescale(rescale, shift)  

24.      hwc2chw_op = CV.HWC2CHW()  

25.      type_cast_op = C.TypeCast(mstype.int32)  

26.        

27.      # 使用map映射函数，将数据操作应用到数据集  

28.     mnist_ds = mnist_ds.map(operations=type_cast_op, input_columns="label", num_parallel_workers=num_parallel_workers)  

29.     mnist_ds = mnist_ds.map(operations=resize_op, input_columns="image", num_parallel_workers=num_parallel_workers)  

30.     mnist_ds = mnist_ds.map(operations=rescale_op, input_columns="image", num_parallel_workers=num_parallel_workers)  

31.     mnist_ds = mnist_ds.map(operations=rescale_nml_op, input_columns="image", num_parallel_workers=num_parallel_workers)  

32.     mnist_ds = mnist_ds.map(operations=hwc2chw_op, input_columns="image", num_parallel_workers=num_parallel_workers)  

33.        

34.      # 进行shuffle、batch操作  

35.      buffer_size = 10000  

36.      mnist_ds = mnist_ds.shuffle(buffer_size=buffer_size)  

37.      mnist_ds = mnist_ds.batch(batch_size, drop_remainder=True)  

38.    

39.      return mnist_ds  

通过运行上例代码就可以完成我们的第1步了，预备好我们的数据集，现在准备我们的主角LeNet网络。

1. 网络(LeNet5)

LeNet 诞生于1994年，是最早的卷积神经网络之一，并且推动了深度学习领域的发展。自从1988年开始，在许多次成功的迭代后，这项由 Yann LeCun完成的开拓性成果被命名为 LeNet5。LeNet5是一种用于手写体字符识别的非常高效的卷积神经网络，这与Mnist数据集正好匹配。

• LeNet5结构

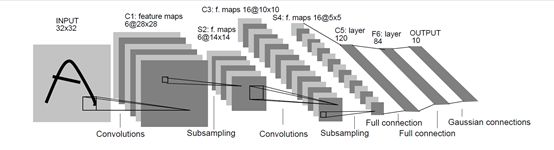
首先是最最具有代表性的LeNet5网络结构图，从图中我们可以看到每层之间的变换，包括卷积、池化和全连接三种变换方式。这里我们简单介绍下三种变换方式对图像的作用。

卷积：首先卷积需要一个卷积核，卷积核的卷积计算过程就相当于一个滤波器，可以让图像的边缘更加明显。

池化：通常图像中相邻的像素具有很大相似性，因此通过卷积后输出的像素值也依然有此特性，这意味着卷积输出的信息中存在冗余，池化可以做到减少图像中的信息冗余。

全连接：全连接在整个卷积神经网络中起到分类器的作用，卷积和池化是将原始数据映射到隐层特征空间中，全连接层就是把学到的特征映射到样本空间中，以此实现分类。

图2：LeNet5结构图

介绍了不同变换方式，下面我们通过数值计算，看一下图像的变化。

• LeNet5的数值计算

如图2中所示，是LeNet卷积网络的整体流程图，整体包含8个网络层，下面我们将了解每一层的计算。

输入层：我们使用的数据集是MNIST数据集，该数据集中的样本数据都是规格为32×32的灰度图，我们以1个样本图片为例。那么我们输入的图片规格就是1×1×32×32，表示一个通道输入1个32×32的数组。

C1层：C1层中数组规格为6×1×28×28，从1×1×32×32卷积得到。首先需要6个批次的卷积数组，每一个批次中都有1个规格为5×5的卷积数组，卷积步幅默认为1。即卷积数组规格为6×1×5×5。

该卷积层共有6+1×5×5×6=156个参数，其中6个偏置参数。这一层网络**有6×1×28×28=4704个节点，每个节点和当前层5×5=25个节点相连，所以本层卷积层共有6×(1×28×28)×(1×5×5+1)=122304个全连接。

S2层：S2层的数组规格为6×1×14×14，从1×1×28×28卷积得到。使用的是2×2，步幅为1的最大池化操作，所以并不改变批次数，只是将每一个输入数组从28×28降到14×14的输出数组。

该池化层共有6×2=12个可训练参数，以及6×(1×14×14)×(2×2+1)=5880个全连接。

C3层：C3层的数组规格为16×1×10×10，从6×1×14×14卷积得到。输出通道数数改变，所以卷积数组需要16批卷积数组，每一批中有6个卷积核与输入通道对应，每一个卷积数组规格都是5×5，步幅为1。即卷积数组规格为16×6×5×5。

该卷积层共有16+1×5×5×16=2416个参数，其中16个偏置参数。这一层网络**有16×1×10×10=1600个节点，每个节点和当前层5×5=25个节点相连，所以本层卷积层共有16×(1×10×10)×(1×5×5+1)=41600个全连接。

S4层：S4层的数组规格为16×1×5×5，这一层池化与S2层池化设置相同。所以输出数组只改变每一个数组的规格，不改变数量。

该池化层共有16×2=32个可训练参数，以及16×(1×5×5)×(2×2+1)=2000个全连接。

C5层：C5层是规格为120×1的一维向量，那么需要将S4层数组转换成一维向量，输入的数组规格是1×（16×1×5×）=1×400。使用全连接层将1×400转为1×120的向量。在全连接层中，每一个节点计算处结果后，都需要再经过激活函数计算，得出的值为输出的值。

该连接层共有5×5×16=400个输入节点，参数个数为5×5×16×120+120=48120个，输出节点120个。

F6层：F6层是规格为84×1的一维向量，与C5层计算相同，也是通过全连接层计算得到。为什么要转成84个神经元向量呢，如下图中所示，是所有字符标准格式，规格为12×7.所以有84个像素点，然后使用F6层的向量与这些标准图计算相似度。

该连接层共有120个输入节点，参数个数为120×84+84=10164个，输出节点84个。

图3：字符标准图

输出层：该连接层共有84个输入节点，参数个数为84×10+10=850个，输出节点10个。

输出层使用Softmax函数做多分类，在Softmax用于多分类过程中，它将多个神经元的输出，映射到（0，1）区间中，可以看作是每一个类别的概率值，从而实现多分类。Softmax从字面上来看，可以分成Soft和max两部分。Softmax的核心是Soft，对于图片分类来说，一张图片或多或少都会包含其它类别的信息，我们更期待得到图片对于每个类别的概率值，可以简单理解为每一个类别的可信度；max就是最大值的意思，选择概率值最大的当作分类的类别。

• LeNet5的创建

上面我们通过图片和每层的计算解析了LeNet的结构和计算，下面我们开始用MindSpore撸它，上代码：

1.   import mindspore.nn as nn  

2.   from mindspore.common.initializer import Normal  

3.     

4.   class LeNet5(nn.Cell):  

5.       """ 

6.       Lenet网络结构 

7.       """  

8.       def __init__(self, num_class=10, num_channel=1):  

9.           super(LeNet5, self).__init__()  

10.          # 定义所需要的运算  

11.          self.conv1 = nn.Conv2d(num_channel, 6, 5, pad_mode='valid')  

12.          self.conv2 = nn.Conv2d(6, 16, 5, pad_mode='valid')  

13.          self.fc1 = nn.Dense(16 * 5 * 5, 120, weight_init=Normal(0.02))  

14.          self.fc2 = nn.Dense(120, 84, weight_init=Normal(0.02))  

15.          self.fc3 = nn.Dense(84, num_class, weight_init=Normal(0.02))  

16.          self.relu = nn.ReLU()  

17.          self.max_pool2d = nn.MaxPool2d(kernel_size=2, stride=2)  

18.          self.flatten = nn.Flatten()  

19.    

20.      def construct(self, x):  

21.          # 使用定义好的运算构建前向网络  

22.          x = self.conv1(x)  

23.          x = self.relu(x)  

24.          x = self.max_pool2d(x)  

25.          x = self.conv2(x)  

26.          x = self.relu(x)  

27.          x = self.max_pool2d(x)  

28.          x = self.flatten(x)  

29.          x = self.fc1(x)  

30.          x = self.relu(x)  

31.          x = self.fc2(x)  

32.          x = self.relu(x)  

33.          x = self.fc3(x)  

34.          return x  

35.    

36.  # 实例化网络  

37.  net = LeNet5()  

通过运行上例代码就可以完成我们的第2步了，构建出了我们的模型，现在最主要的两大部件准备就绪，继续向下走。

1. 损失函数

如果就此开始训练，也就是执行第3步，通过初始的模型分类之后会存在分类错误的情况，为了提升模型的分类能力，我们需要能够调整模型参数，那么损失函数就出现了，损失函数可以通过数值很直观的展示模型此刻的性能，损失值越大表示模型性能越差。

• 损失函数原理

损失函数也有很多，为什么是SoftmaxCrossEntropyWithLogits损失函数呢？我们再来了解一下本次项目的目的：图像分类。那么分类中的损失函数是怎么计算的，它是计算logits和标签之间的softmax交叉熵。使用交叉熵损失测量输入概率（使用softmax函数计算）与类别互斥（只有一个类别为正）的目标之间的分布误差，具体公式可以表示成图4。

图4：SoftmaxCrossEntropyWithLogits表达式

参数说明：

• logits (Tensor) - Tensor of shape (N, C). Data type must be float16 or float32.
• labels (Tensor) - Tensor of shape (N, ). If sparse is True, The type of labels is int32 or int64. Otherwise, the type of labels is the same as the type of logits.

第一个参数logits：就是神经网络最后一层的输出，如果有batch的话，它的大小就是[batchsize，num_classes]，单样本的话，大小就是num_classes；第二个参数labels：实际的标签，大小同上。

• 损失函数的调用

上面是解释了该类型损失函数的基本计算过程，但在我们需要使用进行调用的时候还是相当简便的，使用MindSpore撸它，上代码：

1.   from mindspore import nn  

2.   loss = nn.SoftmaxCrossEntropyWithLogits(sparse=True, reduction='mean')  

这里参考官网API我们对做了如上的设置：选择使用稀疏格式为`True`，损失函数的减少类型选择为`mean`。

1. 优化器

上面损失函数的作用是可以计算出模型的性能，我们也需要明确一点，Loss值是我们要最小化的值。那么如何才能够让Loss值最小化呢？就需要我们调整网络模型中的参数，让模型更适应所训练的数据集，这也是模型的训练过程，在其中调整参数的就是优化器。

• 优化器原理

本次训练中我们使用的是Momentum，也叫动量优化器。为什么是它？下面我们了解下它的工作原理，表达式如图5所示

图5：Momentum表达式

上面表达式中的grad、lr、p、v 和 u 分别表示梯度、learning_rate、参数、矩和动量。其中的梯度是通过损失函数求导得出的，在训练过程中得到的Loss是一个连续值，那么它就有梯度可求，并反向传播给每个参数。Momentum优化器的主要思想就是利用了类似移动指数加权平均的方法来对网络的参数进行平滑处理的，让梯度的摆动幅度变得更小。

参数说明：

• params (Union [list [Parameter], list [dict]]) - 当params是一个dict列表时，“params”、“lr”、“weight_decay”和“order_params”是可以解析的键。lr：可选。如果键中有“lr”，将使用相应学习率的值。如果没有，将使用 API 中的learning_rate；weight_decay：可选。如果键中有“weight_decay”，将使用相应的权重衰减值。如果没有，将使用 API中的weight_decay；order_params：可选。如果键中有“order_params”，则该值必须是参数的顺序，并且在优化器中将遵循该顺序。dict中没有其他键，并且 'order_params' 值中的参数必须在组参数之一中； grad_centralization：可选。“grad_centralization”的数据类型是 Bool。如果“grad_centralization”在键中，将使用设置的值。如果不是，则grad_centralization默认为 False。该参数仅适用于卷积层。
• learning_rate (Union [float, Tensor, Iterable, LearningRateSchedule ] ) – 学习率的值或图表。当 learning_rate是一个 Iterable 或者一维的 Tensor 时，使用动态学习率，那么第 i步将取第 i 个值作为学习率。当 learning_rate 为LearningRateSchedule 时，使用动态学习率，训练过程中会根据LearningRateSchedule 的公式计算第 i 个学习率。当 learning_rate是零维的浮点数或张量时，使用固定学习率。不支持其他情况。浮点学习率必须等于或大于 0。如果类型learning_rate是 int，它将被转换为float。
• 动量(float) – float类型的超参数，表示移动平均线的动量。它必须至少为 0.0。
• weight_decay (int, float) – 权重衰减（L2 惩罚）。它必须等于或大于 0.0。默认值：0.0。
• loss_scale (float) – 损失比例的浮点值。它必须大于 0.0。一般情况下，使用默认值。仅当使用FixedLossScaleManager进行训练并且FixedLossScaleManager中的 drop_overflow_update设置为 False 时，该值需要与FixedLossScaleManager中的 loss_scale相同。默认值：1.0。
• use_nesterov (bool) - 图5中的2和3公式和参数use_nesterov相关，如果设置`use_nesterov = True`，则按照公式2计算，如果设置`use_nesterov = False`，则按照公式3计算。
• 优化器的调用

废话不多说，直接使用MindSpore撸它，上代码：

1.   from mindspore import nn  

2.   lr = 0.01  

3.   momentum = 0.9  

4.   net_opt = nn.Momentum(network.trainable_params(), lr, momentum)  

参考以上的参数解析，我们对Momentum优化器的使用如上面代码。此时我们完成了首图中的`2->4->6`的训练过程，该过程就是重复网络分类图片、计算损失函数、梯度反向传播、参数调整的过程。

1. 精度

虽然损失函数值可以衡量网络的性能，对于图片分类的任务，使用精度可以更加准确的表示最终的分类结果。

• 精度表达式

精度表达式比较简单，也好理解。分母是总样本数，分子是分类正确的样本总数，对应于首图中5。

图6：Accuracy表达式

• 精度调用

精度值也会随着训练过程实时更新，使用MindSpore撸他，上代码：

1.   from mindspore import nn  

2.   metrics = nn. Accuracy()

3.   model = Model(net, net_loss, net_opt, metrics={"Accuracy": Accuracy()})  

基于上面代码，可以使用Accuracy功能。Acc也是我们需要最大化的值。

本篇内容中每一段代码为了展示不同接口的调用做了调整，完整的图像分类任务脚本可以参考：docs/sample_code/lenet/lenet.py · MindSpore/docs - Gitee.com

总结

本次内容是以图像分类任务为例，对于任务首先要明白数据集的内容和结构，以及要完成的目标，然后根据目标选择基本网络、损失函数、优化器和精度这几部分，这些的选择和设置是非常重要的，会直接影响到模型的训练和最终的性能。其他任务也都可以基于本示例进行扩展升级，谢谢赏读。