机器学习笔记1——决策树算法(上)
一、概述
决策树是机器学习中比较经典的算法,跟我们日常使用的if-else的思想有些相似。
而决定分到哪一类则是根据哪个属性用于分类最明显为依据。(可以用信息熵Entropy、信息增益Gain或基尼系数Gini等来度量。)
例如,我们一般看一个人的身份可以根据性别,年龄,长相,身材等等因素。在这个例子里,性别显然是最明显的区分要素,因此我们会首先根据性别这一属性将样本分为“男”,“女”,“中性”。
随后可能较为明显的是身高,身高理论上是连续的值,在我们的常规思维中是难以进行分类的,所以我们要主动地进行转换。比如,把原本连续的150~190的身高分布转换成“高(175以上)”,“中等(160到175)”和“矮(160以下)”三类。
然后再依次按照越来越不明显的原则往下设计。
二、如何选择优先分类的属性?
上文中提到了三个指标,我们一一来分析。
1.信息熵(Entropy)
熵的概念我们在高中化学中已经接触过(1947年由香农提出),用来衡量某成分的不稳定度,成分越混乱,熵值越高。因此,信息熵则是用来衡量数据的不稳定度。
H(X) = −∑ Pilog(Pi)*
例如,在第一组样本中,100人中,男女各占50人;第二组样本中,男生90人,女生10人,我们从两个样本中各抽取一人来判断性别。
| 组别 | 男生 | 女生 |
|---|---|---|
| A | 50 | 50 |
| B | 90 | 10 |
很显然,当我们预测从第二组中拿出的样本时,预测成功的信心更大,因为这里有90%的男生,所以随机抽取一人是男生的概率就非常大,因此我们认为这个样本就不是很混乱,对应的熵值也就越低。而对于第一组来说,男女各占50%,所以随机抽取一人,在没有别的判断依据时,我们难以预测。
我们可以计算两组的信息熵,组A的信息熵是:
H(Xa) = − Pmalelog(Pmale) - Pfemalelog(Pfemale)
= -log(0.5)
≈ 0.693
H(Xb) = − Pmalelog(Pmale) - Pfemalelog(Pfemale)
= -0.9log(0.9) + -0.1log(0.1)
≈ 0.325
所以第一组的信息熵更大,信息更混乱。
从这个例子中我们还可以看出,二元分类中如果样本是50%对50%的,那时是最难判断的,理论上信息熵应该会是最大的,这也就意味着H(X)在0.5处取值会最大,我们来看看这个函数的图示。
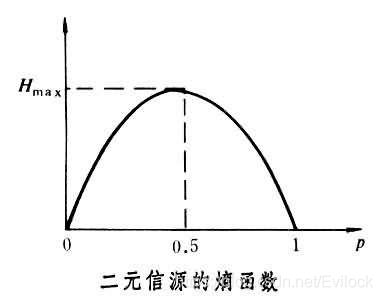
实时证明确实在0.5处取值最大,而且当p = 0或者1时,我们知道样本中只有一种可能,也就是肯定是男生或者女生,此时信息熵应该一点都不混乱,也就是H(X) = 0。由图可知确实是如此。
2.信息增益(Gain)
信息增益意思是我们挑选的属性使得实际上也是使用信息熵。信息增益意味着我们选择了某一属性后,使得原来的集合混乱度有多少的改善。我们先来看公式
Gain(S,A) = H(S) - H(A)
H(S) = H(S-all)
H(A) = H(S-1) + H(S-2) + H(S-3) + …
H(S)代表结果的混乱程度
H(A)表示某条件明确了之后的混乱程度
所以,Gain代表的就是某条件确定了之后,集合的混乱程度改善了多少
如果Gain很大,说明在A条件确定了之后,集合的混乱度大大减小,使我们期望得到的结果;如果Gain很小,说明对混乱程度没有什么改善,所以就无所谓了。
其中前者表示的就是我们之前求得信息熵;后者则表示我们以某一个分类为前提条件,对以该条件得到的分类下的每一项求信息熵。即信息熵-条件熵,举例来说
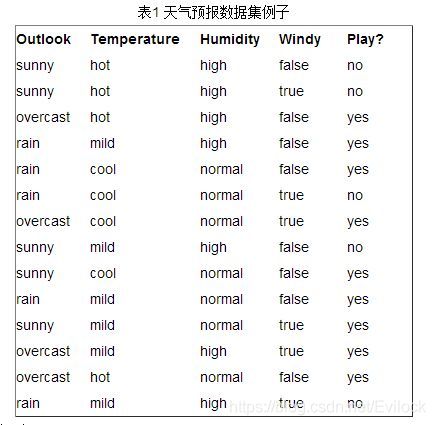
我们以Humidity为前提条件,求Temperature的信息增益
H(Humidity) = -5/14log(5/14) - 9/14log(9/14)
H(A) = 4/14H(H-hot) + 6/14H(H-mild) + 4/14H(H-cool)
=4/14 (-log(0.5)) + 6/14 (1/3log(1/3)+2/3log(2/3))
+ 4/14(1/4og(1/4 + 3/4log(3/4)))**
所以ID3采用的就是判断信息增益大小的方法来进行特征提取
信息增益发生的问题有:
1)回到公式本身来

当极限情况下A将每一个样本都分到一个节点当中去的时候,后面的括号部分为0.也就是条件熵部分为0,而条件熵的最小值为0,这意味着该情况下的信息增益达到了最大值,一定会选择特征A。然而,我们知道这个特征A显然不是最佳选择。
2)C4.5不能用于回归
3)模型容易过拟合
4)模型计算复杂度太高了
5)有一个严重的问题,样本分类多的值比样本少的值更容易有更大的信息熵。比如说,现在有12个人,6个男生,6个女生;4个中国人,4个日本人,4个韩国人。性别和国籍的判别都是完全不确定的变量,但是两者的信息熵就不相同。更偏向与取值特征更丰富的选项。通常遇到这种情况,我们就有必要为这种不公平的特征设置权重了。此时就需要使用信息增益比来衡量。
3.信息增益比
信息增益比 = 惩罚参数 * 信息增益
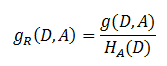
其中
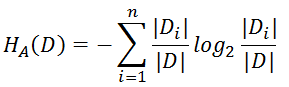
这个虽然解决了之前的问题,但其实信息增益比还是有点偏向于取值较少的情况。这是C4.5采用的方法,本质与ID3差不多,但效果确实有提升。
接下来我们介绍CART方法,这个方法非常高级,解决了大部分之前存在的问题,而且既可以做回归又可以做分类。
3.基尼系数(Gini)
用基尼系数提取特征,基尼系数的公式如下
Gini§=∑Pk(1−Pk)=1−∑Pk^2
而CART使用的是二叉树,所以每次计算的时候其实只需要:
Gini§ = 2p(1-p)
*不是而分类的话,有D个样本,K个类别,则Gini(D) = 1-∑(|Ck|/|D|)^2
所以Gini(D,A)=|D1|/|D|Gini(D1)+|D2|/|D|Gini(D2)
而CART是二叉树,当遇到多分类的时候,就通过二叉树的叠加即可。
对于连续特征的离散化,CART树采用基尼系数
CART分类树建立算法
输入:阈值 最少样本量 训练数据集
输出:CART分类树
STEP 1:构件空树
STEP 2:递归构建树——按照最优切分点来分类
递归终止条件::
1)子数据及少于最少样本量
2)基尼系数下降到小于阈值
CART回归树建立算法
核心思想:区分为若干子空间,取各个空间中的均值作为输出值
其他的都和分类树差不多
三、决策树的剪枝(C4.5/CART)
1.预剪枝
为熵设置一个阈值,低于这个阈值就停止剪枝,直接进行分类
2.后剪枝
删除子树,用叶子结点替代
3.CART剪枝
简单的说就是,在原本生成的树一点点剪掉子树,然后看看怎么剪成什么样的时候准确度最高
