Python机器学习--分类\回归--决策树算法
决策树算法类型
决策树是一系列算法,而不是一个算法。
决策树包含了 ID3分类算法,C4.5分类算法,Cart分类树算法,Cart回归树算法。
决策树既可以做分类算法,也可以做回归算法。因此决策树既可以解决分类问题,也可以解决回归问题。
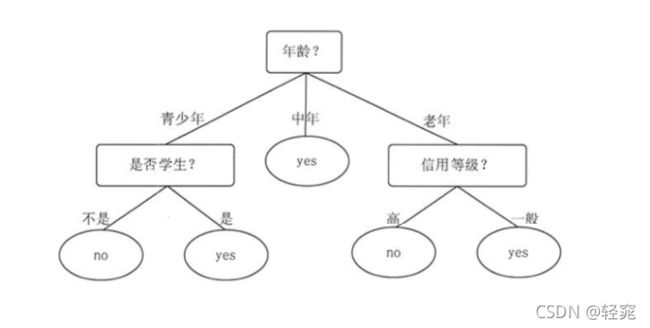
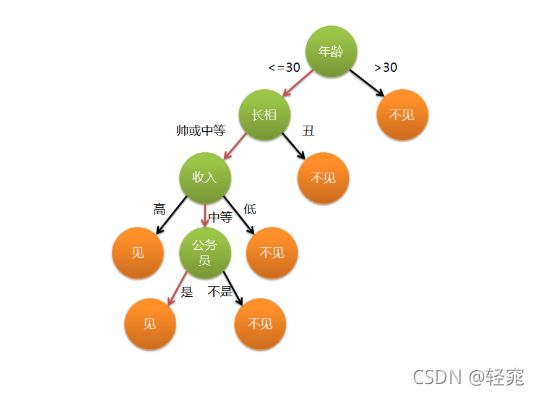
一般来讲,在决策树中,根节点和分节点使用方块表示,而叶子节点使用椭圆表示。
决策树的关键点在于如何取建立出一个树,如何建立出一个在可以达成目标的前提下深度最浅的树
决策树中不同算法的介绍
CLS、ID3、C4.5、CART四种,其中ID3、C4.5、CART都采用贪心方法,其中决策树以自顶向下递归的分治方法构造,并且大多数决策树算法都采用这种自顶向下的方法。所谓贪心方法,通俗的讲就是在选取根节点时把所有的都计算一遍,使用穷举的方法找到最优
CLS算法简介
CLS是最早期的决策树算法,它并没有给出怎样确定根节点,只是给出了创建决策树的具体方法,其他三种算法是对CLS的优化和延伸。
CLS的基本流程:
- 生成一棵空的决策树和一个训练集样本属性集。
- 若训练集中所有样本都属于同一类,则生成一个叶子节点,终止算法。
- 根据某种策略从训练集样本的属性中选择属性作为分裂属性,生成测试节点。
- 根据测试节点的取值不同分为不同的的分支。
- 从训练样本的属性中删除已经分裂过的属性。
- 辗转至步骤 2 重复操作,直到分裂出所有的数据都属于同一类停止。
通俗点讲:
CLS就是从数据集中随机选择一列(等意于一个特征或一个属性),如果他所有的取值都属于同一类别,就终止,否则删除该列,再根据删除的列的取值分支进行分裂,直至所有的分裂都属于同一类别。
ID3分类算法简介
ID3主要针对于属性选择问题,使用信息增益来选择分裂属性的评断标准
ID3分类算法特点:
- 只能实现分类算法
- 特征必须是离散数据
- 树是可以多分支(多叉树)---一个特征属性 有多个取值,每个取值是一个分支
- 是多分类算法[标签数量可以大于2 活动的结果:进行 or 取消 or 暂定 ]
ID3分类算法缺点:
优先选择属性取值多的特征进行分裂
什么是信息增益熵?
信息量的计算公式:![]()
信息出现的概率越大,表示它信息量就越少,即出现概率越小,信息量越大。比如当概率等于1时,信息量就等于 -log(1)
![]()
在信息论中,通常指数是以2为底,因此只需考虑图中的红色线即可。
![]()
对于熵的理解可以简化为 加权平均信息量。特征S的取值有N种,而每种可能出现的概率乘以他的信息量并相加就是加权平均信息量。
条件熵
相当于条件概率
1.先计算结果的熵值。
2.在计算已知某特征条件下的结果结果的熵值。
举例:
假设某 特征存在三个取值,标签有两个取值。
1.先计算出该特征三个取值的概率:p1,p2,p3.
2.计算每一个取值下结果的熵值。
3.条件熵=三个取值结果下的三个熵值的加权平均。
ID3分类算法信息增益
信息增益的作用就是确定作为根节点的特征,用结果的熵值减去已知特征的情况下结果的条件熵计算公式:
Gain(特征) = H(结果) - H( 结果 | 特征 )
结论:选择信息增益最大的作为根节点
总结:
1.假设存在一个包含若干特征,一个标签的数据集。
2.对标签计算出结果熵值。
3.对所有特征中的取值计算出对应结果的条件熵。
4.计算每个特征的信息增益,选出最大值作为根节点。
5.将分裂完成的特征列删除,如果结果为同一类,结束算法。
6.如果不是同一类,则继续计算剩下的特征的信息增益,选取最大的作为下一次分裂的特征。
7.重复计算信息增益,选择特征进行分裂,直到所有叶子节点为同一类结束。
ID3分类算法原理计算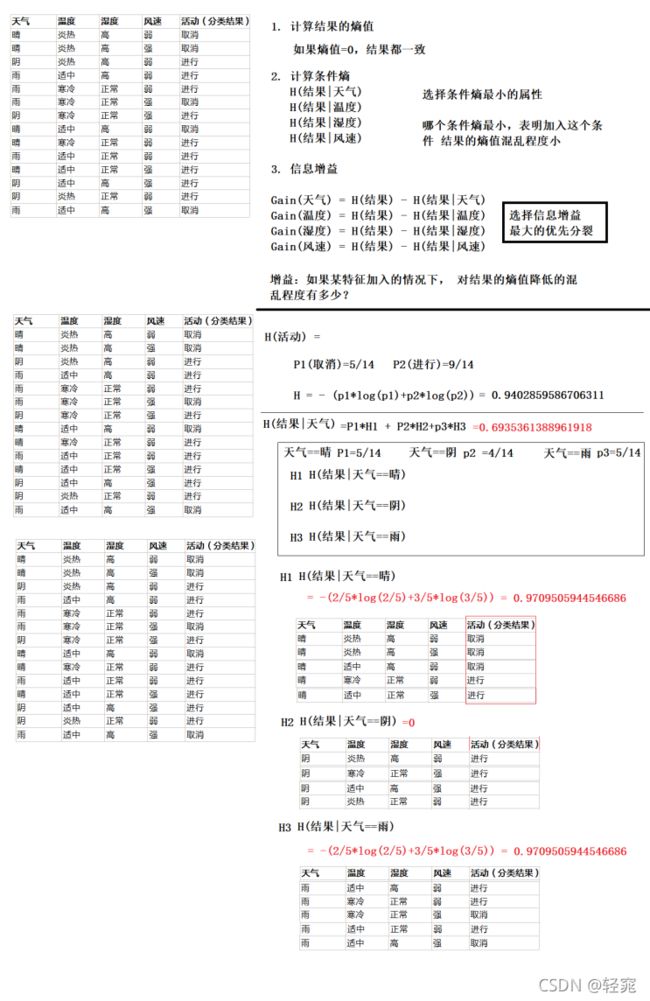
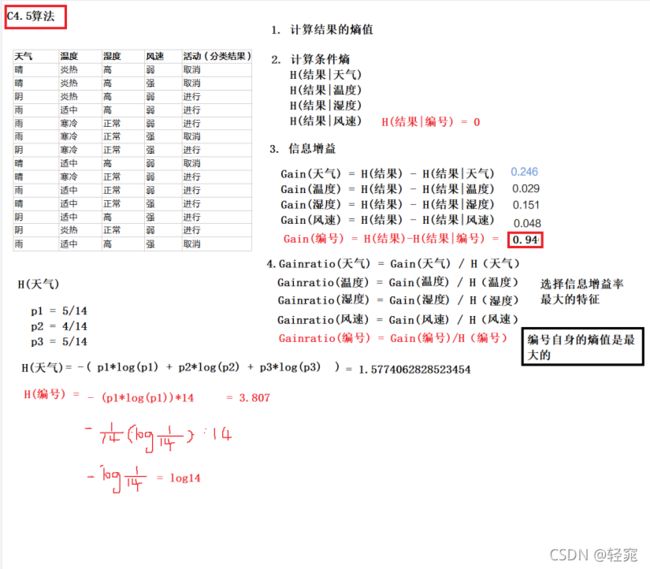
C4.5分类算法简介
在ID3的基础上做了一些优化,通过使用信息增益率选择分裂属性,克服了ID3算法中通过信息增益无法处理很多属性值的数据的缺陷,信息增益率能够处理离散数据和连续数据,还能处理有确实属性的训练数据。
C4.5分类算法的特点
- 使用 信息增益率 作为分裂属性的评断标准
- 只能实现分类算法
- 能够处理连续数据的特征
- 树是可以多分支(多叉树)
- 是多分类算法
C4.5分类算法信息增益率(Gainratio)
信息增益率能够有效避免倾向于选择拥有多个属性值的样本
信息增益率公式:
Gainratio(特征) = Gain(特征) / H(特征)
选择增益率最大的特征作为根节点,使用流程和使用信息增益的流程一样
C4.5分类算法连续值处理
对于连续型数据的处理,不再使用信息增益率处理,而使用下面的这种方式:
- 假设某一特征中存在N个连续型数据。
- 将这一列数据去重后升序排序。
- 求出相邻两个值的均值,这样可以得到N-1个数据。
- 先使用第一个数据,计算小于第一个数据的值的条件熵和大于第一个数据的条件熵,在计算出该数据的信息增益。
- 以此计算剩下N-2个数据的信息增益。
- 当比较信息增益,选择最大的信息增益对应的属性值作为分裂点(比如有一列为密度的特征,当密度=0.318时信息增益是最大的,选择这个点为分裂点,这是它的取值就变成了小于0.318的和大于等于0.318的两类,再进行分裂)

C4.5分类算法缺点
通过上述处理,只能将连续特征进行二分处理,依然是只能实现分类算法,下面的算法又进行了改进,可以实现处理分类算法和回归算法。
C4.5分类算法原理计算
C4.5分类算法总结
信息增益率可以处理属性值特别多的特征;离散数据在经过分裂后会被删除,但是经过连续值处理后的数据分裂后不会被删除,后续还能作为属性划分。
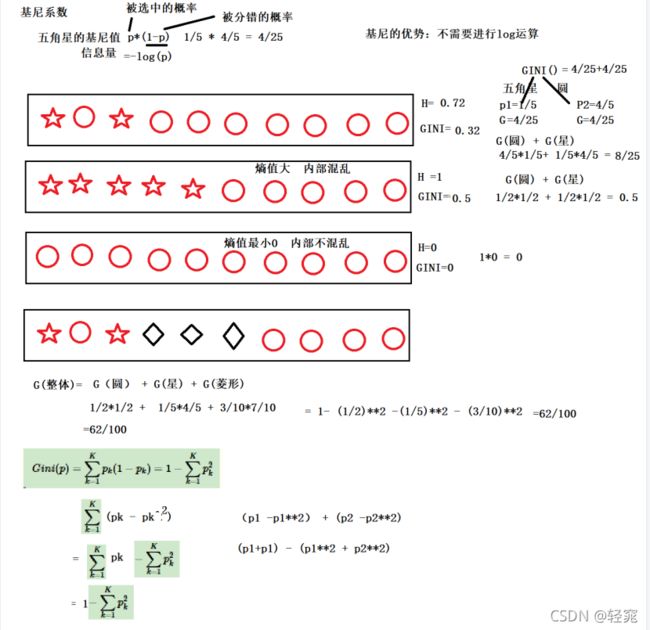
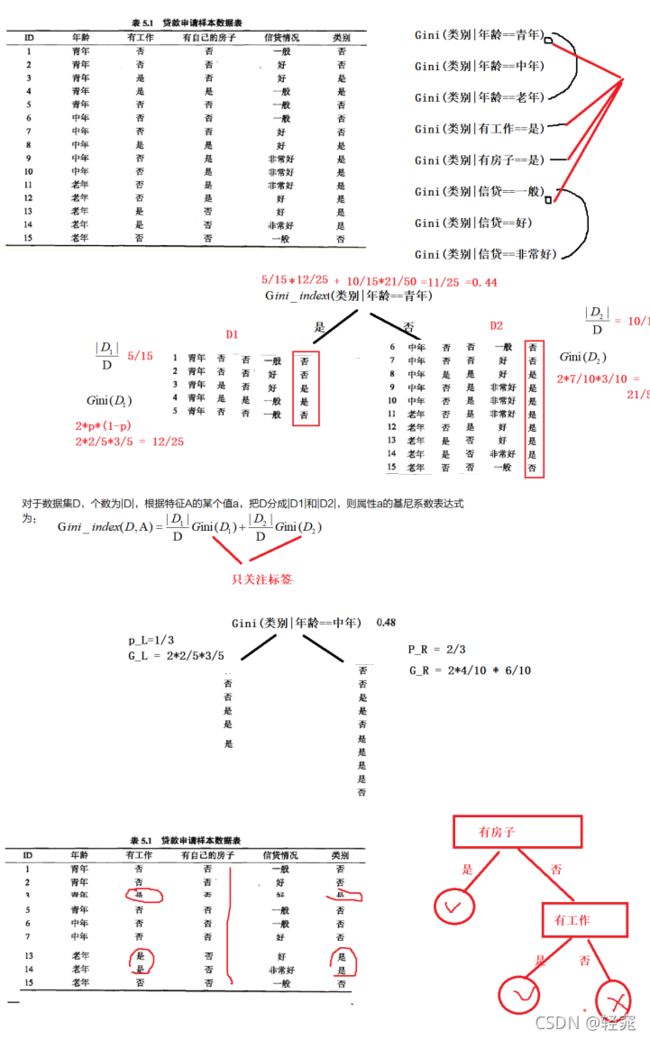
CART分类算法基尼系数
基尼系数公式:![]()
基尼值代表了模型的不纯度,基尼值越小,则不纯度越低,特征越好。基尼值=样本被选中的概率-样本被分错的概率,用公式表示为 ![]()
基尼系数针对的是二分类,只会分为是或否。对于某一个特征,特征里面的所有取值都要计算一下对应结果的基尼值,然后计算基尼系数,选取最小的作为分裂节点
基尼系数只能在分类算法中使用
CART回归算法简介
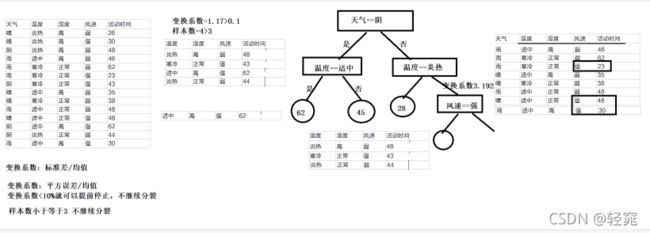
CART回归算法平方误差
使用平方误差计算的是二分类回归算法,对连续性的标签进行处理,具体步骤为:
- 先选取某一个特征的若干个取值进行计算,类似于条件熵,在已知取值的情况下结果的平均误差。
- 选取平均误差小的作为分裂节点。
- 在判断左节点如果小于等于三条,则终止左子树的分裂,如果大于3,就继续判断该节点的变换系数,如果小于0.1就停止左子树分裂,否则继续分裂,右子树同理。
- 删除分裂过的特征,继续判断剩下的特征哪个取值平均误差最小。
- 直到变换系数小于0.1或行数小于3时停止,如果停止时标签仍然有两个以上的值,那么就取其均值作为结果。
CART回归算法原理计算
平方误差计算流程:
变换系数计算流程:
- 变换系数也称为离散系数或者变化系数,离散系数等于标准差除以均值,但是在平均误差中使用的是平均误差除以均值。
CART回归算法缺失值处理
在缺失值处理中使用最多的就是权重,下面以信息增益为例:
- 比如某一特征有缺失值,在计算该列的信息增益时要先把有缺失值的行去掉,计算剩下的行信息增益
- 其余特征有缺失值也是这样计算
- 通过对比计算出的信息增益,选择最大的作为根节点,但是这只是选择根节点的方法
- 选择出根节点后,根据取值进行分裂
- 比如根节点列有两个缺失值,分了三个分支,每个分支上的数据数目分别为7,5,3;这个时候要把缺失值加回来,因为缺失值对应的行还有结果信息,后续选择还需要使用,每个分支都要加上两个缺失值,三个分支上的数据就变成了9,7,5;
- 数据每一行的权重都是1,但是有缺失值就不一样了,由于每个分支上的无缺失数据有7,5,3;两个缺失值的权重就变成了:分支数据个数/(7+5+3+2),也就是7/15,5/15,3/15,无缺值的权重还是1
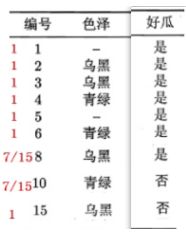
- 在根据权重分别计算剩余特征的信息增益,去除要计算特征的缺失值,首先计算结果的熵,H(结果) = -p1log(p1) - p2log(p2),公式中的概率p需要根据权重来计算,p = 非缺失值权重 / 总权重 ,p1 = (4 + 7/15) / (5 + 2 * 7/15),条件熵的计算同理,再选择信息增益最大的进行分裂,重复加权计算的过程
缺失值的处理还是比较麻烦的,在数据量足够多的情况下,还是建议直接删除有缺失的行
决策树基于sklearn实现
决策树特点
使用垂直于特征值进行分裂
可以产生树结构,可视化效果好【0基础人可以理解算法预测过程】
不需要标准化
可以自动忽略掉对目标没有贡献的属性
CART分类\回归算法区别
CART可以实现分类和回归算法,sklearn中分别为Classification 和Regression Tree
CART算法特点
分类算法中使用基尼系数,作为分裂属性的评断标准。
回归算法中使用平法误差,作为分裂属性的评断标准。
树是二叉树。
是多分类算法
基尼与熵的关系:基尼与熵的趋势一致,基尼也成为熵之半,因此基尼的运算更加简单。
决策树-分类树基于sklearn实现
import pandas as pd
from sklearn.model_selection import train_test_split
#分类树
from sklearn.tree import DecisionTreeClassifier
#数据集的读取
work_data=pd.read_csv('./HR_comma_sep.csv')
work_data['department1']=work_data['department'].astype('category').cat.codes
work_data['salary1']=work_data['salary'].astype('category').cat.codes
x=work_data[['satisfaction_level', 'last_evaluation', 'number_project','average_montly_hours', 'time_spend_company', 'Work_accident','promotion_last_5years', 'department1','salary1']]
y=work_data['left']
#数据拆分
X_train, X_test, y_train, y_test = train_test_split(
x, # 特征
y, # 标签
test_size=0.2, # 给测试集分配多少数据
random_state=1,
stratify=y, # 分层 保证拆分前后各类别的比例一致
)
#决策树
start_time=time.time()
dt = DecisionTreeClassifier()
dt.fit(X_train,y_train)
print("决策树预测准确率", dt.score(X_test, y_test))
end_time=time.time()
print("决策树用时", end_time-start_time)
决策树-回归树基于sklearn实现
import pandas as pd
from sklearn.model_selection import train_test_split
#回归树
from sklearn.tree import DecisionTreeRegressor
#数据的获取
selery_data=pd.read_excel('./job.xlsx',sheet_name=1)
name = selery_data['语言'].astype("category").cat.categories
selery_data['语言1']=selery_data['语言'].astype("category").cat.codes
selery_data['学历1']=selery_data['学历'].astype("category").cat.codes
x1=selery_data[['语言1','工作经验(年)','学历1']].values
y1=selery_data['最高薪资(元)'].values
#数据的拆分
X_train1, X_test1, y_train1, y_test1 = train_test_split(
x1, # 特征
y1, # 标签
test_size=0.2, # 给测试集分配多少数据
random_state=1,
# stratify=y1, # 分层 保证拆分前后各类别的比例一致
)
#回归树
dt=DecisionTreeRegressor()
alg.fit(X_train1, y_train1)
print("回归树准确率", alg.score(X_test1, y_test1))
决策树最优参数的寻找
import pandas as pd
from sklearn.model_selection import train_test_split
#分类树
from sklearn.tree import DecisionTreeClassifier
#网格搜索
from sklearn.model_selection import GridSearchCV
#数据集的读取
work_data=pd.read_csv('./HR_comma_sep.csv')
work_data['department1']=work_data['department'].astype('category').cat.codes
work_data['salary1']=work_data['salary'].astype('category').cat.codes
x=work_data[['satisfaction_level', 'last_evaluation', 'number_project','average_montly_hours', 'time_spend_company', 'Work_accident','promotion_last_5years', 'department1','salary1']]
y=work_data['left']
#数据拆分
X_train, X_test, y_train, y_test = train_test_split(
x, # 特征
y, # 标签
test_size=0.2, # 给测试集分配多少数据
random_state=1,
stratify=y, # 分层 保证拆分前后各类别的比例一致
)
#网格搜索最优参数探索
dt = DecisionTreeClassifier()
param_grid = {"criterion": ["gini", "entropy"], "max_depth": [3, 5, 6, 7, 9]}
gird = GridSearchCV(dt, param_grid)
gird.fit(X_train, y_train)
print("最好的参数", gird.best_params_)
#交叉验证探索最优参数
from sklearn.model_selection import cross_val_score
for max_depth in [3, 5, 6, 7, 9]:
for criterion in ["gini", "entropy"]:
dt = DecisionTreeClassifier(max_depth=max_depth, criterion=criterion)
score = cross_val_score(dt, X_train, y_train, cv=5).mean()
# print(score)
print("深度是{} 准则{} 得分是{}".format(max_depth, criterion, score))
#分类树
start_time=time.time()
dt = DecisionTreeClassifier()
dt.fit(X_train,y_train)
print("决策树预测准确率", dt.score(X_test, y_test))
end_time=time.time()
print("决策树用时", end_time-start_time))
决策树输出树
# 将算法模型dt 导出到 dot文件中
from sklearn.tree import export_graphviz
export_graphviz(dt, 'titanic.dot',
feature_names=["pclass", "age", "sex"],
feature_names=["舱位", "年龄", "性别"],
max_depth=5, # 树的深度
class_names=['死亡', '生存'] # 类别名称
)
#使用以下命令将生成的 titanic.dot转为图片格式
# dot -Tpng tree.dot -o tree.png