作品集：基于 CNN 卷积神经网络的图像分析（运用python）

摘要：图像处理 (image processing) 又称为影像处理，是用计算机对图像进 行达到所需结果的技术。常见的处理有图像数字化、图像编码、图像增强、图像复原、图像分割和图像分析等。而图像作为人类感知世界的视觉基础，是人 类获取信息、表达信息和传递信息的重要手段，因此，图像处理技术对于现代 生活有着不可或缺的作用。提供的训练数据集给出了 1990 张 32X32=1024 像素的 RGB 图片，同时有着对应图片的标签；测试集包括499张图片数据，可是没有对应的标签。本文通过 python 语言，对如下两个问题进行分析处理。

第一个问题是简单指标的统计，由数据集可知，共 5 类，计算每一类图片 的 R、G、B 均值，标准差及其方差共 45 个指标。

第二个问题是建立图片判别模型，通过卷积神经网络，判别得出 499 张图 片中属于 5 类中哪个类别，通过图片判别模型得出来的效果为训练集准度为 0.9542，测试集拟合准度为 0.7839，采取了 adam 算法,早停法等来提高模型的 泛化能力，将训练集和验证集比例分为 9:1，其中训练集的准度为 0.9542，说 明模型已经训练得比较好，同时验证集准度为 0.7839 说明模型具有一定的泛化 能力，最后将模型代入对测试集 499 张图片生成标签，进行判别。

关键词：卷积神经网络，准度，图像判别

目录

1.问题一的求解

1.1 问题分析

1.2 数据处理结果

2. 问题 2 的建模与求解

2.1 问题分析

2.2 数据预处理

2.3 模型建立

2.3. 1 卷积神经网络

2.3.2 Adam 算法

2.3.3 数据增强

2.4 训练和判别结果

2.4.1 超参数的设置

2.4.2 模型设置

2.4.3 训练结果

2.4.4 判别结果

3.总结

4.附件

5.源码

---

1.问题一的求解

1.1 问题分析

问题一为求每类图片的 R、G、B 均值及标准差，同时本文选定自定义指标为方差，故 需要求每类图片的 R、G、B 均值，方差及标准差。

1.2 数据处理结果

通过 python 语言将文件进行提取分析处理，得出每一类图片的 R、G、B 均值，标准差 及其方差 (保留了两位小数) 如表 1,2 和 3 所示：

表 1 每类图片R 均值、方差及标准差

标签	R  mean _	R  var _	R  std
0	135.29	4007.71	63.31
1	122.68	4772.69	69.08
2	123.66	3315.48	57.58
3	127.58	4158.66	64.49
4	118.45	2972.93	54.52

表 2 每类图片G 均值、方差及标准差

标签	G  mean _	G  var _	G  std
0	143.65	3723.21	61.02
1	116.69	4723.56	68.73
2	125.33	3183.45	56.42
3	116.62	4068.28	63.78
4	116.51	2668.93	51.66

表 3 每类图片 B 均值、方差及标准差

标签	B  mean _	B  var _	B  std
0	149.83	4510. 18	67. 16
1	114.2	4983.24	70.59
2	107. 16	3943.93	62.8
3	105.7	4270.66	65.35
4	94.3	2807. 1	52.98

2. 问题 2 的建模与求解

2.1 问题分析

提供的训练数据集给出了 1990 张 32X32=1024 像素的 RGB 图片，同时给出了对应的标签， 目前卷积神经网络在图像识别具有比较大的优势，故本文采用卷积神经网络，将图片 数据作为输入数据训练卷积神经网络，从而得出对应的模型参数来判别测试集 499 张图片 的序号，建立起图片的判别模型。

2.2 数据预处理

观察数据可知，没有缺失值，故不需要进行缺失值处理。

对训练集数据的处理：对训练集的数据进行 0-1 标准化，再转换成 4 维张量； 对测试集数据的处理：对测试集数据进行独热编码。

上述步骤完成后，分离出训练集和验证集数据，训练集和验证集比例为 9 :1，用于后 续评估模型是否准确和是否发生过拟合。

通过数据集生成图片可知，标签 0 为飞机，标签 1 为汽车，标签 2 为鸟，标签 3 为猫， 标签 4 为鹿。

2.3 模型建立

2.3. 1 卷积神经网络

卷积神经网络由三部分构成。第一部分是输入层。第二部分由n 个卷积层和池化层的 组合组成。第三部分由一个全连结的多层感知机分类器构成。

卷积神经网络与普通神经网络的区别在于，卷积神经网络包含了一个由卷积层和子采 样层构成的特征抽取器。在卷积神经网络的卷积层中，一个神经元只与部分邻层神经元连 接。在 CNN 的一个卷积层中，通常包含若干个特征平面，每个特征平面由一些矩形排列的 神经元组成，同一特征平面的神经元共享权值，这里共享的权值就是卷积核。卷积核一般 以随机小数矩阵的形式初始化，在网络的训练过程中卷积核将学习得到合理的权值。共享 权值 (卷积核) 带来的直接好处是减少网络各层之间的连接，同时又降低了过拟合的风险。 子采样也叫做池化，通常有均值子采样和最大值子采样两种形式。子采样可以看作一种特殊的卷积过程。卷积和子采样大大简化了模型复杂度，减少了模型的参数。因此卷积神经 网络在图像识别中得到广泛应用。

本问题中，涉及到图像识别分类，故选择卷积神经网络算法。

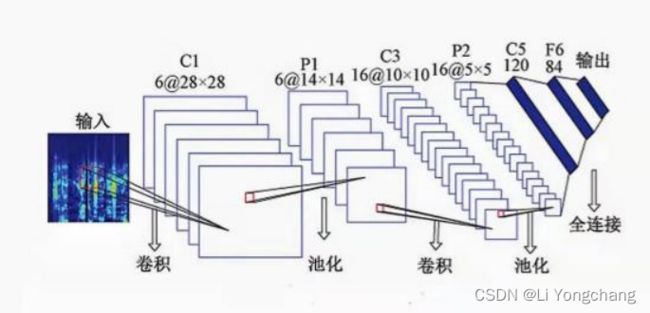
其中，通用的卷积网络求解如图一所示：

 

图一 通用的卷积网络图

2.3.2 Adam 算法

Adam 算法相对传统的随机梯度下降不同，通过计算梯度的一阶矩估计和二阶矩估计而 为不同的参数设计独立的自适应学习率。有着两大优点，第一个优点是为每一个参数保留 一个学习率以提升在稀疏梯度上的性能，能有效避开局部最小值和鞍点；第二个优点是基 于权重梯度最近量级的均值为每一个参数适应性地保留学习率。故本文用Adam 作为优化算 法。

2.3.3 数据增强

数据增强通过对训练图片进行变化可以得到泛化能力更强的神经网络，同时可以在一 定程度上增加训练集数量。本文采用数据增强，适当地增加训练集容量，同时在一定程度 上提高神经网络的泛化能力。本文中数据增强中设置垂直和水平随机转换图片的范围设置 为 0.2。

2.4 训练和判别结果

2.4.1 超参数的设置

超参数 Epoch (使用训练集的全部数据对模型进行一次完整训练) 为 200；Batch_size (批的大小) 为 64；loss(损失函数)选择交叉熵；选择 adam 算法作为优化算法； 同时为 了防止神经网络发生过拟合，即当网络在训练集表现得越来越好，但测试集已经开始变差， 设置了早停法。

卷积神经网络模型参数如表四所示：

表四 卷积神经网络的参数设置

Layer (type)	Output Shape	Param #
conv2d (Conv2D)	(None, 32, 32, 32)	896
batch_normalization (Batch Normalization)	(None, 32, 32, 32)	128
conv2d_ 1 (Conv2D)	(None, 32, 32, 32)	9248
batch_normalization_ 1 (Batch Normalization)	(None, 32, 32, 32)	128
max_pooling2d (Max Pooling2D)	(None, 16, 16, 32)	0
dropout (Dropout)	(None, 16, 16, 32)	0
conv2d_2 (Conv2D)	(None, 16, 16, 64)	18496
batch_normalization_2 (Batch Normalization)	(None, 16, 16, 64)	256
conv2d_3 (Conv2D)	(None, 16, 16, 64)	36928
batch_normalization_3 (Batch Normalization)	(None, 16, 16, 64)	256
max_pooling2d_ 1 (Max Pooling2D)	(None, 8, 8, 64)	0
dropout_ 1 (Dropout)	(None, 8, 8, 64)	0
conv2d_4 (Conv2D)	(None, 8, 8, 128)	73856
batch_normalization_4 (Batch Normalization)	(None, 8, 8, 128)	512
conv2d_5 (Conv2D)	(None, 8, 8, 128)	147584
batch_normalization_5 (Batch Normalization)	(None, 8, 8, 128)	512
max_pooling2d_2 (Max Pooling2D)	(None, 4, 4, 128)	0
dropout_2 (Dropout)	(None, 4, 4, 128)	0
flatten (Flatten)	(None, 2048)	0
dense (Dense)	(None, 5)	10245
Total params: 299,045 Trainable params: 298, 149 Non-trainable params: 896

2.4.2 模型设置

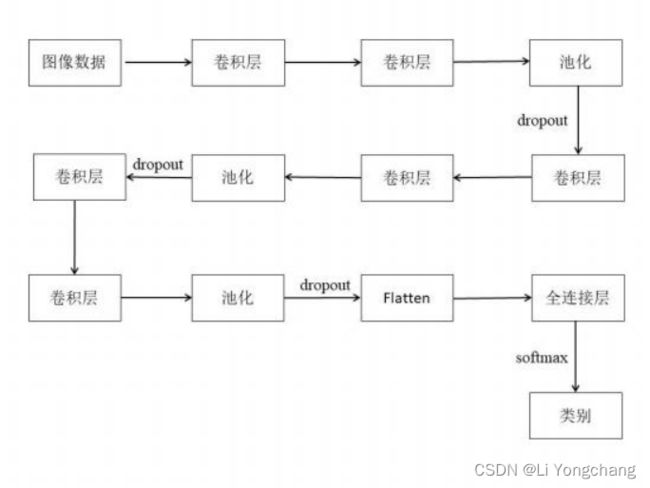
本文采取的卷积神经网络如图二所示：

 

图二 卷积神经网络层数设置

2.4.3 训练结果

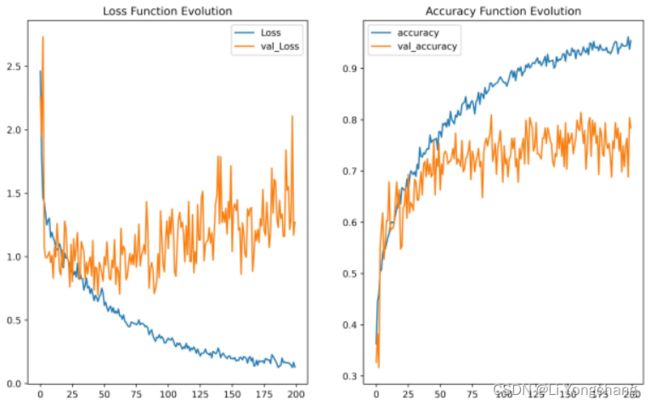
取训练最佳的模型，训练集拟合准度 0.9542，测试集拟合准度为 0.7839。如图三所示， 总体上在训练集的损失不断减少和精度不断提高的同时，验证集的损失函数也在降低，同时验证集的精度也在不断上升。没有出现明显的过拟合现象。

图三 训练和验证集损失函数和精度

模型判断出错的可能原因：

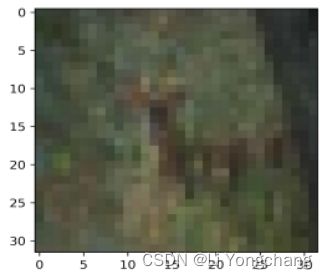
1.部分图片的像素非常模糊不清，即使是人观看，也会判别不清。如图四所示： 2.训练集的数据太少，模型训练得不够完善

3.受限于机身配置，没有对模型进行更深层数的设置

 

图四 模糊图片

2.4.4 判别结果

通过生成的模型，对 tedata.txt 文件的测试数据对 RGB 数据进行拟合，产生生成 499张图片的标签，并放置于 submission.csv 文件，详见附件。

3.总结

本文的模型基于卷积神经网络，模型优点在于大大简化了模型复杂度，减少了模型的 参数，同时相比全连接的神经网络分类图像，它能从训练数据中推断空间结构。本文采用 了 adam 算法、早停法来防止模型出现局部最小和鞍点；采用了数据增强来解决训练集过少 的问题，同时一定程度上提升了模型的泛化能力。通过图片判别模型得出来的效果为训练 集准度为 0.9542，测试集拟合准度为 0.7839，采取了 adam 算法,早停法等来提高模型的泛 化能力，将训练集和验证集比例分为 9 :1，其中训练集的准度为 0.9542，说明模型已经训 练得比较好，同时验证集准度为 0.7839 说明模型具有一定的泛化能力。

而模型缺点在于，受限于训练集数量集过少，同时受限于机身配置，没有对模型进行 更深层数的设置。

4.附件

1.submission.csv

2.pythonhw.ipynb (python 源码文件)

3.trdata.txt

4.tedata.txt

5.trlab.txt

6.teseqn.txt

5.源码

5.源码
#import module
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
import tensorflow as tf
from  tensorflow.keras   import  datasets,   layers,  models,  regularizers, optimizers,callbacks
from tensorflow.keras.preprocessing.image import ImageDataGenerator
import numpy as np
import matplotlib.image as mpimg
import seaborn as sns
%matplotlib inline
#load data and data cleaning
x = pd.read_table('trdata.txt',header=None)
x.loc[ :,0]
x = x.loc[ :,0].str.split(',',expand=True)
x[0] = x.loc[ :,0].str.replace('[','')
x[3071] = x.loc[ :,3071].str.replace(']','')
x = x.apply(pd.to_numeric)
r = np.array(x.loc[:,0:1023]).reshape(1990,32,32,1)
g = np.array(x.loc[ :,1024:2047]).reshape(1990,32,32,1)
b = np.array(x.loc[:,2048:3071]).reshape(1990,32,32,1)
x_train = np.concatenate((r,g,b),axis=3)
x_test = pd.read_table('tedata.txt',header=None)
x_test.loc[ :,0]
x_test = x_test.loc[:,0].str.split(',',expand=True)
x_test[0] = x_test.loc[ :,0].str.replace(' [','')





x_test[3071] = x_test.loc[ :,3071].str.replace(']','')
x_test = x_test.apply(pd.to_numeric)
r_1 = np.array(x_test.loc[:,0:1023]).reshape(499,32,32,1)
g_1 = np.array(x_test.loc[:,1024:2047]).reshape(499,32,32,1)
b_1 = np.array(x_test.loc[:,2048:3071]).reshape(499,32,32,1)
x_test = np.concatenate((r_1,g_1,b_1),axis=3)
a = pd.read_table('trlab.txt',header=None,sep=' ')
b = a.stack()
y= np.array(b)
y.reshape(1990,1)
# one-hot encoding
y_train = tf.keras.utils.to_categorical(y,5)
x['label'] = y
#第一小问,求每一类 RGB 的平均值
x['label'] = y
answer = []
for i in [0,1,2,3,4]:
df =  x[x['label'] == i]
for j in [0,1,2]:
A = df.loc[ :,1024*j:j*1024+1023]
A = np.array(A).flatten()
mean = round(np.mean(A),2)
answer.append(mean)
var = round(np.var(A),2)
answer.append(var)
std = round(np.std(A),2)
answer.append(std)
if j == 0 :
print('标签为 '+ str(i)+ f' 的 R 的平均值为{mean}.')





print('标签为 '+ str(i)+ f' 的 R 的方差为{var}.')
print('标签为 '+ str(i)+ f' 的 R 的标准差为{std}.')
elif j == 1 :
print('标签为 '+ str(i)+ f' 的 G 的平均值为{mean}.')
print('标签为 '+ str(i)+ f' 的 G 的方差为{var}.')
print('标签为 '+ str(i)+ f' 的 G 的标准差为{std}.')
else:
print('标签为 '+ str(i)+ f' 的 G 的平均值为{mean}.')
print('标签为 '+ str(i)+ f' 的 G 的方差为{var}.')
print('标签为 '+ str(i)+ f' 的 G 的标准差为{std}.')
answer_1                                                                        = pd.DataFrame(np.array(answer).reshape(5,9),columns= ['R_mean','R_var','R_std',' G_mean','G_var','G_std','B_mean','B_var','B_std'])
answer_1.to_csv ('answer_1.csv',index=True)
# Scale the data
X_train = x_train / 255.0
X_test = x_test / 255.0
#split the train and valid
x_train, x_val, y_train, y_val = train_test_split(x_train, y_train, test_size=0.1, random_state=0)
#constant
EPOCHS=200
NUM_CLASSES = 5
def build_model() :
model = models.Sequential()

#1st blocl
model.add(layers.Conv2D(32, (3,3), padding='same',
input_shape=x_train.shape[1:], activation='relu'))





model.add(layers.BatchNormalization())
model.add(layers.Conv2D(32, (3,3), padding='same', activation='relu')) model.add(layers.BatchNormalization())
model.add(layers.MaxPooling2D(pool_size= (2,2)))
model.add(layers.Dropout(0.2))

#2nd block
model.add(layers.Conv2D(64, (3,3), padding='same', activation='relu')) model.add(layers.BatchNormalization())
model.add(layers.Conv2D(64, (3,3), padding='same', activation='relu')) model.add(layers.BatchNormalization())
model.add(layers.MaxPooling2D(pool_size= (2,2)))
model.add(layers.Dropout(0.3))


#3d block
model.add(layers.Conv2D(128, (3,3), padding='same', activation='relu')) model.add(layers.BatchNormalization())
model.add(layers.Conv2D(128, (3,3), padding='same', activation='relu')) model.add(layers.BatchNormalization())
model.add(layers.MaxPooling2D(pool_size= (2,2)))
model.add(layers.Dropout(0.4))


#dense
model.add(layers.Flatten())
model.add(layers.Dense(NUM_CLASSES, activation='softmax'))
return model
model.summary()
early_stopping = callbacks.EarlyStopping(
min_delta=0.001, # minimium amount of change to count as an improvement





patience=20, # how many epochs to wait before stopping
restore_best_weights=True,
)
#image augmentation
datagen = ImageDataGenerator(
width_shift_range=0.2,
height_shift_range=0.2,
horizontal_flip=True,
)
datagen.fit (x_train)
model = build_model()
model.compile(loss='categorical_crossentropy',
optimizer='Adam',
metrics=['accuracy'])
#train
batch_size = 64
r       =       model.fit_generator(datagen.flow(x_train,       y_train,
batch_size=batch_size),
epochs=EPOCHS,
verbose=1,validation_data= (x_val,y_val) )
score = model.evaluate(x_val, y_val,
batch_size=batch_size)
print("\nTest score:", score[0])
print('Test accuracy:', score[1])
#data visualization
plt.figure(figsize= (12, 16))
plt.subplot(2, 2, 1)
plt.plot(r.history['loss'], label='Loss')





plt.plot(r.history['val_loss'], label='val_Loss')
plt.title('Loss Function Evolution')
plt.legend()


plt.subplot(2, 2, 2)
plt.plot(r.history['accuracy'], label='accuracy')
plt.plot(r.history['val_accuracy'], label='val_accuracy')
plt.title('Accuracy Function Evolution')
plt.legend()
plt.savefig('loss and accuracy',dpi=600, bbox_inches='tight') #predict
y_pred = model.predict(x_test)
classes_y=np.argmax(y_pred,axis=1)
h = pd.Series(classes_y)
df = pd.DataFrame(h,columns= ['类别'])
df.to_csv ('submission1.csv', index=True)
print("Your submission was successfully saved!")