通过深度学习偏微分方程模型估计剩余使用寿命：使用潜变量的 退化的动力学解释框架/PINN 在发动机寿命预测的应用 文献总结和内容概要

一、引言

  发动机的PHM就是基于传感器数据来研究和预测发动机的健康状态，只要任务是做RUL预测。目前有三种方法：数据驱动方法、纯物理模型方法和混合方法。
  本文中的混合方法受PINN的启发，是数据驱动和数据模型方法两者的结合。
  数据驱动方法的优点：在不知道背后的物理原理时，仅根据海量数据就可以找出隐含在数据中的数据和特征，就能得到很好的RUL预测模型；缺点：缺乏可解释性
  物理模型方法的优点：高度准确可靠，可解释性强；缺点：在一个系统上学到的模型不一样适合另一个模型，即模型的普适性很差，
  DL在发动机的PHM中应用的一大问题是缺乏模型的可解释性，即用户给DL提供数据，神经网络给出一个模型结果，用户不能对该模型结果进行解释，导致的结果就是不信任神经网络给出的模型，只能通过性能指标比如回归问题中的误差；分类问题的精确率、召回率等。现在已经有一些第三方的软件或包提供特征相关性的信息，即给出特征之间的相关性，从而更加有利于做特征选择，有利于提高所得模型的质量。但它们的适用范围有限，即只专注于自然语言或图像处理的分类模型，并且所给出的特性相关性对神经网络根据输入特征训练的这个过程无关。

特征选择的重要性：机器学习模型的好坏取决于你所拥有的数据。这就是为什么数据科学家可以花费数小时对数据进行预处理和清理。他们只选择对结果模型的质量贡献最大的特征。这个过程称为“特征选择”。特征选择是选择能够使预测变量更加准确的属性，或者剔除那些不相关的、会降低模型精度和质量的属性的过程。
数据与特征相关被认为是数据预处理中特征选择阶段的一个重要步骤，尤其是当特征的数据类型是连续的。那么，什么是数据相关性呢？
数据相关性：是一种理解数据集中多个变量和属性之间关系的方法。使用相关性，你可以得到一些见解，如：
一个或多个属性依赖于另一个属性或是另一个属性的原因。
一个或多个属性与其他属性相关联。

  要做混合模型，在DL-PHM模型的基础上，有两个因素使得模型的可解释性更加困难，一是模型要引入时间变量，二是引入系统退化的物理定律与输入特征之间的显式关系。
  根据PINN的启发，本文的框架将监测数据和时间变量映射为 与系统退化相关的隐变量，再将这一项引入损失函数来训练DNN模型。训练好的模型可以作为发动机健康状态的定量和定性的估计器。也就是说，类似于给定PDE方程和初始条件来求解PDE，该框架在给定初始特征值（相当于PDE的初始条件）后给出特定时间下的RUL值。
  目前大多数的DL模型只做单一任务，很少有能够同时执行预测和诊断两个任务的框架。虽然有一些这方面的工作，但各自有很大的局限性，比如网络会很复杂，对数据的质量要求很高以及缺乏结果的可解释性。
本文的贡献：

1. 提出了混合方法，旨在缩小纯数据方法和纯物理方法在PHM应用的差异（目的）
2. 显式地将监测数据和时间与退化过程关联，并使用类似于PDE的损失函数（创新点1-解决系统物理场与模型输入之间的显式关系）
3. 由于显式使用时间，使该框架可以直接反应出数据的时间特性。（创新点2-解决将时间作为显式变量）
4. 可同时执行诊断和预测任务（成果1-可同时完成诊断和预测的任务）
5. 通过可视化潜在变量（监测数据和时间变量的映射）来解释退化，提高模型的可解释性。（成果2-增加了DL模型的可解释性）

二、物理信息神经网络PINN

  PINN是2018年Raissi等人发表在《Journal of Computational Physics》期刊上的《Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations》即《物理信息神经网络：用于解决涉及非线性偏微分方程的正向和逆向问题的深度学习框架》，该框架可以在给定初始或边界条件下求解和发现PED。Raissi等人在文章中以Burgers方程为例，给出了3个可能的应用：

1. 在给定初始和边界条件下求解一个已知的PDE；
2. 根据来自目标空间的数据找到控制已知PDE的参数；
3. 仅根据目标空间的数据找到并求解一个未知的PDE。

  目前，将PINN应用于PHM的主要困难在于缺乏将数据与发动机退化关联起来的PDE，但从第三个应用中可以看出，无需有任何关于所研究系统的物理定律等先验知识，仅从数据本身恢复或创建一个PDE。这一点也是本文作者的灵感来源。

三、本文所提出的框架

3.1当前DL-PHM所面临的三个问题

  获得可同时产生 可解释的健康评估器和传统的预测指标的 DL-PHM模型面临的困难有以下几条：

1. 如果只是单纯的数据驱动方法，而不引入关于退化物理特性的数学模型，模型的可解释性依然是一个很大的问题；
2. DL-PHM方法一般不把数据作为输入变量，但发动机的退化一定是随时间而逐渐加剧的，因此在训练无时间输入变量的DL模型时，关于系统的退化信息很可能丢失；
3. 由于RUL预测是一个监督任务，需要为训练数据设置标签，即要设置 退化过程开始的时间点。一般有两种方式，一是故障前的固定时间，二是一个特定的性能变量超过预定的阈值。但无论哪一种方法，会有一个缺点那就是用这种标签训练的DL模型会将对应的行为的权重偏大，这样会在用新的测试数据时产生错误。

3.2 本文相应的解决方案

  针对问题一，引入潜变量，进而通过潜在空间表示来探索系统的退化物理特性，从而引入了物理定律，增强模型的可解释性；针对RUL，在惩罚函数中使用时间导数来添加有关退化率的信息；
  针对问题二，该框架将时间作为输入特征，更好地寻找模型的输入特征与退化之间的关系；
  针对第三个问题，该框架也是手动设置标签，但可以赋予所得到模型的可解释性来克服手动引入标签所带来的不确定性。

3.3 DNN框架

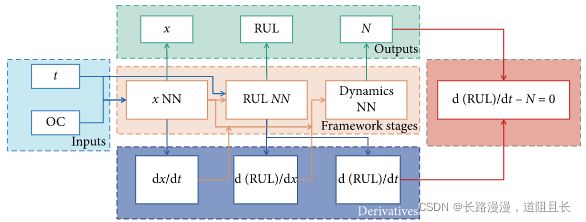
  上图是本文所提出的结合PDE的DNN框架。可以看到，中间浅粉色区域有3个网络，因此可以分为3个阶段来产生RUL估计。

1. 阶段一：$x-NN$：该网络的输入变量是OC（operational conditions运行条件）和时间 $t$ ，输出是潜变量 $x$ 上， $x$ 可能是多维的。该网络有5个隐藏层，每层3个神经元，输出层2个神经元（输出都是 $x$ ）。因此该网络有104个参数。网络所使用的激活函数是tanh。其中潜变量 $x$ 的维度是一个超参数，需要根据所研究的系统进行调整。
2. 阶段二：$RUL-NN$：该网络的输入变量是潜变量 $x$ 和时间 $t$ ，输出是系统的 $RUL$ 。该网络有5个隐藏层，每层10个神经元，输出层1个神经元。因此该网络有481个参数。网络所使用的激活函数是tanh。
3. 阶段三：$Dynamics-NN$动态网络： 该网络的输入变量是潜变量 $x$ 和导数 $dx/dt$、 $dRUL/dt$ ，输出是代表系统动力学的函数 $N$ ， $N$ 之后将进入类似于PDE的惩罚函数中。该网络有5个隐藏层，每层10个神经元，输出层1个神经元。因此该网络也有481个参数。网络所使用的激活函数是ReLu。

  通过自动微分，从第一阶段和第二阶段的NN中获取关于时间的导数 $dx/dt$、 $dRUL/dt$，将其结合形成类似于PDE的惩罚项。惩罚包括RUL的时间导数 $dRUL/dt$与第三阶段的输出 $N$。
惩罚函数如下式所示：$$f:\frac{d(RUL)}{dt}-N(x,\frac{dx}{xt},\frac{d(RUL)}{dx})$$
损失函数为：
$$Cost=\frac{1}{N}\sum _{i=1}^N(RU{L}_i-RU{L}_i{)}^2+\lambda \frac{1}{N}\sum _{j=1}^N{f}^2$$

3.4 所提框架的优势

3.4.1网络框架方面的优势

  通过惩罚函数 $f$ 可以看到，其在RUL和潜变量 $x$ 之间建立了动态关系，而潜变量 $x$ 是通过OC和 $t$ 通过第一阶段的网络得到的，即通过OC和变量 $t$ 得到隐变量 $x$ ，以PDE的形式引入RUL关于 $t$ 和 $x$ 的导数，从而找到未知的PDE，即发动机所遵循的物理特性，增强了模型的可解释性。

3.4.2输入变量方面的优势

1. 将系统的运行条件OC和时间 $t$ 作为输入变量。类比求解PDE，OC代表PDE的初始条件，而 $t$ 代表希望获得RUL值的未来的时间点。例如 $t=0$ 时，网络与普通的DL方法一样，只是根据当前的OC来预测的。
2. 引入潜变量的优势
   • 降低维度：将OC和 $t$ 融合为一个变量，有助于找到对结果影响更大的特征。
   • 作为Dynamic-NN的输入变量：若没有潜变量 $x$，根据OC可能有很多导数，引入潜变量后，就可以减少输入Dynamic-NN的导数数量，从而减少网络的参数和训练时间
   • 消除数据的冗余和噪音：降低数据之间的相关性

  需要注意的是，该框架中的第三个阶段即Dynamic-NN是直接从时间中发现未知的PDE，如果有已知的退化方程，可直接使用已知方程的形式构建Dynamic-NN。

3.5 模型训练步骤

1. 数据预处理：两个输入变量，一是OC（27个传感器中选14个，这14个才是对RUL建模有意义的）二是时间 $t$，为数据添加RUL标签。
2. 根据被研究系统的可用数据和信息，定义并建立框架。
3. 使用预处理过后的数据集训练模型
4. 根据 $x$ 的维度实现结果可视化

四、研究案例：数据集和硬件

  本文使用的是C-MAPSS的FD001和FD004进行模型的训练。其中每个数据集是由27个传感器变量组成，FD001有一种故障模型和一个运行条件，FD004有两种故障描述和六个运行条件。该数据集中收集到了每个发动机初始以随机未知的健康状态水平开始运行，直到其发生故障。

4.1数据预处理步骤

每个数据集中的27个传感器变量只有14个对系统的RUL建模有意义，因此本文做模型的训练时也只使用了这14个。
原始数据集的处理步骤为：

1. 选择一个发动机从初始点到其故障的完整的数据
2. 对发动机每一个运行周期，添加一列整数时间 $t$ ，取值范围是0-30
3. 为数据集中每一行的 运行数据和时间 创建标签，即从初始点开始的 $t$ 时刻的RUL值。
   例如，对发动机1，其数据集共有192个sample，如果选择周期编号100作为初始点，那么，对于 $t=0$ ，其对应的标签是 $RUL=92$ ；然后，对于 $t=1$ ，其标签是 $RUL=91$ ；以此类推，直到达到 $t=30$ 或直到 $RUL=1$ （即发动机发生故障）。
   其中 $t$ 的取值范围也是一个超参数，本文对0-100周期的预测范围进行了测试，发现模型的性能在时间跨度大于30个周期时明显下降。因此最终确定 $t$ 的上限为30。

五、结果和讨论

5.1对模型性能影响最大的三个超参数

潜变量维度、分配给PDE正则化函数的惩罚权重 $\lambda$ 以及训练步数epoch，对这三个超参数进行联合敏感度分析，


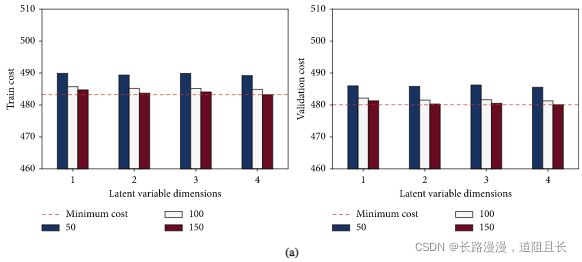
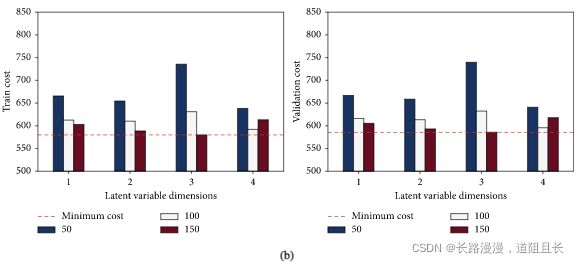
上图是 训练步数和潜变量维度 对代价函数的敏感性分析(a) FD001。(b) FD004。


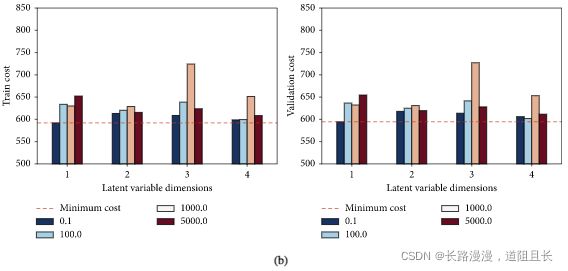
上图是 PDE惩罚权值 $\lambda$ 和潜变量维度对代价函数的联合敏感性分析

通过图中可看出，二维潜变量、150个epoch和惩罚权重 $\lambda$ 为100模型的效果最好。

5.2模型效果

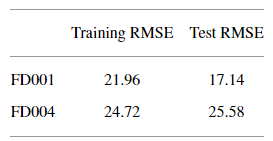
上表显示的是基于所提出的框架训练出的模型 训练和测试数据集的RUL RMSE值

FD001模型对其测试集的平均RMSE值为17.14个周期，而FD004的模型平均产生25.58个周期。 虽然获得的测试集的RMSE值没有 通过其他更复杂的架构获得的那么低，但这些都在本案例研究的可接受范围内。因为本框架的网络参数很少，模型不会过拟合，不需要太多的训练数据。

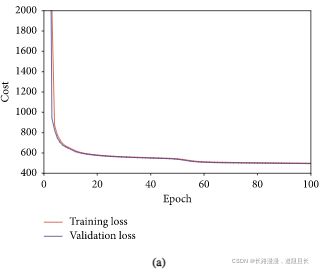
上图是FD001(a)和FD004(b)子数据集训练过程中每个epoch的训练和验证代价 值
从这张图可以看出训练集和验证集的值非常接近，并且最终收敛到一个值，可见模型的泛化能力很好。

5.3 潜在空间表示

由于潜变量的维度为2，根据 $x$ 与RUL的一一对应关系，可以在二维平面内绘制彩色图。

从上图可以看出，对只有一种故障模式的FD001，其RUL遵循一条从低到高的RUL直线路径；对两种故障模式的FD004，RUL值出现分岔也正好说明了这一点。因此可以使用潜在空间来作为系统健康状态的指标。

5.4引入退化开始的阈值和分类器

定义一个“退化开始”的阈值TH，依据所预测出的RUL值与TH的大小，将系统的健康状态分为“健康”和“退化”。依据这两个类别，使用ML的分类算法将系统的健康状态进行分类。这6个分类算法分别为1：nearest neighbors，最邻近算法、2：neural net神经网络、3：Linear SVM线性支持向量机、4：Adaptive Boost自适应增强、5：Random forest随机森林、6：Logistic regression逻辑回归。


由上图可以看到，各种算法的分类器的训练集和验证集的分类性能都随着TH值的提高而下降。其中，选择50周期的TH值作为最长的范围是最好的，且分类器的性能仍能达到90%，在RUL估计上较低的性能可以被看作是模型的预知性和可解释性之间的权衡。

表2 对FD001子数据集，TH=50时机器学习分类器性能

表3 对FD004子数据集，TH=50时机器学习分类器性能
表2和表3列出了TH=50时所有分类器的性能指标。可以看出，最邻近分类器的性能效果是最好的，但出现了过拟合。其余5种分类器中，随机森林的训练时间和false positive指标都很低，因此选择随机森林分类器作为最终的分类器。

5.5使用分类器将潜在空间表示分为健康区和退化区

依照模型输出的RUL预测值是否大于50将该飞行周期下的发动机判定为健康和退化。如下图所示。

FD001和FD004子数据集的基于训练好的随机森林模型的潜在变量分类器决策区: 降级状态(红色)和健康状态(蓝色) (a)FD001训练集 (b)FD001测试集 ©FD004训练集 (d)FD004测试集

六、总结

  本文提出了一个框架，首次将PINN应用于复杂系统中的PHM。所提出的框架允许通过潜在空间表示来解释退化动力学，因此，它是复杂系统中物理信息模型应用的一个有前途的选择。该框架包括总共有1066个参数的深度神经网络，这比更复杂的架构小得多，至少小两个数量级。这有助于减少训练和评估时间，同时防止过度拟合，并使其成为在线和移动设备上部署的合适方法。这个框架建立了时间和传感器变量与类似PDE惩罚函数的退化之间的关系。我们已经表明，获得的二维潜在空间可以作为系统退化过程的健康指标，也可以为工程目的进行直观的解释，以及通过ML模型作为健康状态分类器。此外，所提出的框架解决了应用于PHM的DL技术的两个主要挑战，即 使用时间作为输入变量和从工程角度解释运行条件。本文在 弥合基于统计的PHM和基于物理的PHM之间的差距方面 迈出了一步，它提供的模型不需要临时和第三方软件来解释其结果，并且与系统的退化过程直接相关。所提出的框架是灵活的，因为如果退化过程是可用的话，它可以将可用的退化过程整合到训练过程中。该框架为将这些算法应用于实际复杂系统打开了许多大门，特别是在维护和预防性评估方面。

原文链接： Remaining Useful Life Estimation through Deep Learning Partial Differential Equation Models: A Framework for Degradation Dynamics Interpretation Using Latent Variables