2022第十三届蓝桥杯国赛真题javaB组
文章目录
- 试题A: 重合次数
- 试题B: 数数
- 试题C: 左移右移
- 试题D: 窗口
- 试题E: 迷宫
- 试题F: 小球称重
- 试题G: 背包与魔法
- 试题H: 修路
- 试题I: 围栏
- 试题J: 好数之和
试题A: 重合次数
本题总分:5 分
【问题描述】 在同一天中,从上午6 点13 分22 秒到下午14 点36 分20 秒,钟表上的 分针和秒针一共重合了多少次? 注意时针、分针、秒针都围绕中心做匀速运动。
【答案提交】 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
这道题纯在纸上算的,502次,但是好像错了,关键就在于题目说时针、分针、秒针都围绕中心做匀速运动。那59分59秒的时候分针、秒针重合,0分0秒也重合,中间没有分开,不知道这两秒算1次还是2次,我是当2次计算结果是502。
试题B: 数数
本题总分:5 分
【问题描述】
任何一个大于1 的正整数都能被分解为若干个质数相乘,比如28 = 227
被分解为了三个质数相乘。请问在区间[2333333; 23333333] 中有多少个正整数可以被分解为12 个质数相乘?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
这道题起初代码是这样的,跑了3个半小时没跑出来,最后比赛结束了还在跑。。。
import java.util.Scanner;
public class Main1 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 2333333; 23333333
int n = 0;
for (int i = 2333333; i <= 23333333; i++) {
if (a(i))
n++;
}
System.out.println(n);
}
private static boolean a(int i) {
int n = 0, m = 2;
while (i != 1) {
while (i % m == 0) {
n++;
if (n > 12)
return false;
i /= m;
}
m++;
}
if (i != 1)
n++;
return n == 12;
}
}
然后受大佬启发,明白了一个数的质因数的平方必然小于这个数,如果分解质因数时质数平方已经大于这个数,那么这个数如果不是1就是他质因数中最后一个质数。
例如260分解质因数,首先会分解出两个2,260/2/2=65,再分解出一个5,剩余13,下一个是7,因为7^2大于13,所以13就是260的最后一个质数
所以再代码中a方法中while加上条件 m * m <= i 就可以变快很多。
private static boolean a(int i) {
int n = 0, m = 2;
while (i != 1 && m * m <= i) {
while (i % m == 0) {
n++;
if (n > 12)
return false;
i /= m;
}
m++;
}
if (i != 1)
n++;
return n == 12;
}
试题C: 左移右移
时间限制: 3.0s 内存限制: 512.0MB 本题总分:10 分
【问题描述】
小蓝有一个长度为N 的数组,初始时从左到右依次是1;2; 3; : : : N。 之后小蓝对这个数组进行了M 次操作,每次操作可能是以下2 种之一:
- 左移x,即把x 移动到最左边。
- 右移x,即把x 移动到最右边。
请你回答经过M 次操作之后,数组从左到右每个数是多少?
【输入格式】
第一行包含2 个整数,N 和M。 以下M 行每行一个操作,其中“L x”表示左移x,“R x”表示右移x。
【输出格式】
输出N 个数,代表操作后的数组。
【样例输入】
5 3
L 3
L 2
R 1
【样例输出】
2 3 4 5 1
【样例说明】
样例中的数组变化如下:
[1; 2; 3; 4; 5]
[3; 1; 2; 4; 5]
[2; 3; 1;4; 5]
[2; 3; 4; 5; 1]
【评测用例规模与约定】
对于50% 的评测用例,1<=N; M <= 10000:
对于100% 的评测用例,1 <= N; M <= 200000; 1 <= x <= N:
这道题用双向链表很好做,但是java中不熟悉如何继承linkedlist写一个查找到并删除,所以用了个数组模拟链表。因为n是小于等于20w的,所以假设20w个数全部左移或者全部右移,60w长度也够,题中开了70w,其实没有必要。
思路是从数组25w下标开始存放1-n,然后定义L、R索引,代表头尾指针,也就是数组当前用到了什么位置,如果某个数左移,将他原来下标位置值置为0(用于最后遍历输出),让L所在下标等于这个数,同时L–,右移同理,最终遍历L-R,输出不为0的数。
import java.util.Scanner;
public class Main3 {
public static void main(String[] args) {
int[] map = new int[700000];
int l = 250000, r = 250000;
Scanner sc = new Scanner(System.in);
String s = sc.nextLine();
String[] s1 = s.split(" ");
int n = Integer.parseInt(s1[0]);
int m = Integer.parseInt(s1[1]);
for (int i = 1; i <= n; i++) {
map[r++] = i;
}
String s2;
int nn;
for (int i = 0; i < m; i++) {
s2 = sc.nextLine();
String[] s3 = s2.split(" ");
nn = Integer.parseInt(s3[1]);
int j;
for (j = l - 5; j <= r + 5; j++) {
if (map[j] == nn) {
break;
}
}
if ("L".equals(s3[0])) {
map[--l] = map[j];
map[j] = 0;
} else {
map[r++] = map[j];
map[j] = 0;
}
}
boolean flag = true;
for (int i = l - 5; i <= r + 5; i++) {
if (map[i] != 0) {
if (flag) {
System.out.print(map[i]);
flag = false;
} else {
System.out.print(" " + map[i]);
}
}
}
}
}
试题D: 窗口
时间限制: 3.0s 内存限制: 512.0MB 本题总分:10 分
【问题描述】
在平时使用电脑的过程中,经常会打开各种各样的窗口,各个窗口会在桌 面上重叠,并按照一定的层次关系显示。有的窗口能够看到全部内容,而有的窗口只能看到局部。 现在给定一组操作桌面窗口的过程序列,请你通过ASCII 艺术图来绘制最 后桌面的状态。 已知桌面的大小为N * M,即桌面高度为N 个像素,宽度为M 个像素, 其中左上角坐标为(0; 0),右下角坐标为(N - 1; M - 1)。
对于窗口的操作有如下5 种:
- new 操作- 打开一个新窗口 new [PID] [top] [left] [height] [width] 如:new 12 20 30 80 100 表示打开一个PID 为12 的窗口,窗口左上角的坐标为(20; 30),该窗口宽 度为100 个像素,高度为80
个像素;新创建的窗口,其层级为顶层。- move 操作- 移动一个窗口 move [PID] [vertical] [horizontal] 如: move 12 -5 10 表示将PID 为12 的窗口在垂直方向上移动5 个像素,在水平方向上移 动10 个像素。若窗口左上角原位置为(20;
30),此时则在(15; 40);移动后的窗 口,其层级为顶层。- resize 操作- 改变窗口大小 resize [PID] [height] [width] 如:resize 12 90 110 表示保持左上角坐标不变的情况下,改变PID 为12 的窗口大小,调整为 试题D: 窗口6 第十三届蓝桥杯大赛软件赛决赛Java大学B组
高度90 像素,宽度110 像素;改变大小后的窗口,其层级为顶层。- close 操作- 关闭窗口 close [PID] 如:close 12 表示关闭PID 为12 的窗口;
- active 操作- 激活窗口 active [PID] 如:active 12 表示激活PID 为12 的窗口,此时该窗口的层级被置为顶层。
【输入格式】
第1 行:2 个正整数N; M,表示桌面大小;
第2 行:1个正整数K,表示操作序列的长度;
第3 - K + 2 行:每行一个操作,格式见题目描述。
【输出格式】
第1-N行:每行M 个字符,仅包含‘.’, ‘+’, ‘-’, ‘|’, ‘ ’ 五种字符。 ‘.’ 表示桌面背景,即该部分未被任何窗口覆盖,‘+’表示窗口的四个角,‘-’ 表示窗口的横边, ‘|’ 表示窗口的竖边,‘ ’ 表示窗口内部。
【样例输入】
7 10
8
new 1 0 3 2 5
new 2 4 4 2 5
new 3 3 3 4 6
resize 3 3 6
move 1 0 5
close 2
new 4 1 1 3 5
active 3
【样例输出】
【评测用例规模与约定】
对于100% 的数据,1 <= N; M <= 256; 1 <= K <= 10000:
输入数据保证:- 同一时间不会有两个相同PID 的窗口存在,可能存在关闭某个PID 的 窗口后,再新建一个同样PID 的窗口,PID 的取值范围为1 <= PID <= 100000;
- 同时存在的窗口数量不超过200 个;
- 窗口尺寸不会小于2 * 2,即窗口高度和宽度均不会小于2,不会大于 N * M;
- 窗口在移动过程中,可能有部分界面超出桌面显示范围;
- 所有输入的数值均不超过±100000。
- move resize close 只会对未关闭的窗口操作。
这道题好像在写业务一样,并不难,就是很复杂。
首先定义了一个Window类,类中有pid、top、left、height、width、active属性,active代表这个窗口的层级1位底层,越大越靠上,因为最后对窗口操作完后根据active对存放所有窗口的list排序,然后一次将窗口在屏幕上绘制就可以了。
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;
public class Main4 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s = sc.nextLine();
String[] s1 = s.split(" ");
int n = Integer.parseInt(s1[0]);
int m = Integer.parseInt(s1[1]);
s = sc.nextLine();
int k = Integer.parseInt(s);
ArrayList<Window> list = new ArrayList<>();
int active = 1;
for (int i = 0; i < k; i++) {
s = sc.nextLine();
s1 = s.split(" ");
switch (s1[0]) {
case "new":
list.add(new Window(Integer.parseInt(s1[1]), Integer.parseInt(s1[2]), Integer.parseInt(s1[3]), Integer.parseInt(s1[4]), Integer.parseInt(s1[5]), active++));
break;
case "move":
for (Window window : list) {
if (window.pid == Integer.parseInt(s1[1])) {
window.top += Integer.parseInt(s1[2]);
window.left += Integer.parseInt(s1[3]);
}
}
break;
case "resize":
for (Window window : list) {
if (window.pid == Integer.parseInt(s1[1])) {
window.height = Integer.parseInt(s1[2]);
window.width = Integer.parseInt(s1[3]);
}
}
break;
case "close":
for (int j = 0; j < list.size(); j++) {
if (list.get(j).pid == Integer.parseInt(s1[1]))
list.remove(j);
}
break;
case "active":
for (Window window : list) {
if (window.pid == Integer.parseInt(s1[1])) {
window.active = active++;
}
}
break;
}
}
// 根据窗口顺序排序
list.sort(new Comparator<Window>() {
@Override
public int compare(Window o1, Window o2) {
return o1.active - o2.active;
}
});
char[][] map = new char[n][m];
for (char[] chars : map) {
Arrays.fill(chars, '.');
}
// ,仅包含‘.’, ‘+’, ‘-’, ‘|’, ‘ ’ 五种字符。
// 根据窗口顺序从底向上绘制
for (Window window : list) {
setChar('+', map, window.top, window.left);
setChar('+', map, window.top + window.height - 1, window.left);
setChar('+', map, window.top, window.left + window.width - 1);
setChar('+', map, window.top + window.height - 1, window.left + window.width - 1);
for (int i = 0; i < window.height; i++) {
if (i == 0 || i == window.height - 1) {
for (int j = 1; j < window.width - 1; j++) {
setChar('-', map, i + window.top, j + window.left);
}
} else {
setChar('|', map, i + window.top, window.left);
setChar('|', map, i + window.top, window.width - 1 + window.left);
for (int j = 1; j < window.width - 1; j++) {
setChar(' ', map, i + window.top, j + window.left);
}
}
}
}
for (char[] chars : map) {
System.out.println(chars);
}
}
public static void setChar(char a, char[][] map, int x, int y) {
if (x < 0 || y < 0 || x >= map.length || y >= map[x].length) {
return;
}
map[x][y] = a;
}
}
class Window {
int pid;
int top;
int left;
int height;
int width;
int active;
public Window(int pid, int top, int left, int height, int width, int active) {
this.pid = pid;
this.top = top;
this.left = left;
this.height = height;
this.width = width;
this.active = active;
}
}
试题E: 迷宫
时间限制: 5.0s 内存限制: 1.0GB 本题总分:15 分
【问题描述】
这天,小明在玩迷宫游戏。 迷宫为一个n * n的网格图,小明可以在格子中移动,左上角为(1; 1),右 下角(n; n) 为终点。迷宫中除了可以向上下左右四个方向移动一格以外,还有 m个双向传送门可以使用,传送门可以连接两个任意格子。 假如小明处在格子(x1; y1),同时有一个传送门连接了格子(x1; y1) 和(x2; y2),那么小明既可以花费1 的步数向上下左右四个方向之一走一格(不能 越过边界),也可以花费1 的步数通过传送门走到格子(x2; y2) 去。而对于同一个迷宫,小明每次进入的初始格子是在这n * n 个格子中均匀随机的(当然运气好可以直接随机到终点),他想知道从初始格子走到终点的最短 步数的期望值是多少。
【输入格式】
输入共1 + m行,第一行为两个正整数n;m。 后面m 行,每行四个正整数xi1; yi1; xi2; yi2 表示第i 个传送门连接的两个格 子坐标。
【输出格式】
输出共一行,一个浮点数表示答案(请保留两位小数)。
【样例输入】
2 1
1 1 2 2
【样例输出】
0.75
【样例解释】
由于传送门的存在,从(1; 1) 出发到终点(2; 2) 只需要一步;而从(1; 2) 和 (2; 1) 出发也只需要向下/右走一步;从(2; 2) 出发需要0 步。所以步数期望为 (1+1+1+0)/ (2*2) = 0:75。
【评测用例规模与约定】
对于20% 的数据,保证n;m <= 20; 对于100% 的数据,保证n;m <= 2000; xi1; yi1; xi2; yi2 <= n。
这道题可以反过来想,就是求从终点去这个地图的每个点需要多少步,注意的是这样想传送门就需要反过来使用。然后就是一个广搜,不过走法除了上下左右还有传送门。
首先定义n * n的二维数组map用于存放走到这个位置需要的步数,然后用n * n的二维数组door存放传送门信息,例如题目输入,那么我们使倒退,所以就认为是(2,2)连接(1,1),让door[2][2]=1*n+1,代表此格可以传送至(1,1),其中特殊的是第二个坐标等于n的情况,所以在把数字还原为坐标时需要对第二个坐标特判。如果yy为0,就代表yy=n。
if (door[a.x][a.y] != 0) {
xx = door[a.x][a.y] / n;
yy = door[a.x][a.y] % n;
if (yy == 0) {
xx--;
yy = n;
}
if (map[xx][yy] == 0) {
list.add(new A(xx, yy, a.step + 1));
map[xx][yy] = a.step + 1;
}
}
完整代码:
import java.math.BigDecimal;
import java.util.LinkedList;
import java.util.Scanner;
public class Main5 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int x1, y1, x2, y2;
int[][] door = new int[n + 1][n + 1];
for (int i = 0; i < m; i++) {
x1 = sc.nextInt();
y1 = sc.nextInt();
x2 = sc.nextInt();
y2 = sc.nextInt();
door[x2][y2] = x1 * n + y1;
}
int[] cx = {-1, 1, 0, 0};
int[] cy = {0, 0, -1, 1};
int[][] map = new int[n + 1][n + 1];
map[n][n] = -1;
LinkedList<A> list = new LinkedList<>();
list.add(new A(n, n, 0));
while (!list.isEmpty()) {
A a = list.pop();
int xx, yy;
if (door[a.x][a.y] != 0) {
xx = door[a.x][a.y] / n;
yy = door[a.x][a.y] % n;
if (yy == 0) {
xx--;
yy = n;
}
if (map[xx][yy] == 0) {
list.add(new A(xx, yy, a.step + 1));
map[xx][yy] = a.step + 1;
}
}
for (int i = 0; i < 4; i++) {
xx = a.x + cx[i];
yy = a.y + cy[i];
if (xx > 0 && yy > 0 && xx <= n && yy <= n && map[xx][yy] == 0) {
list.add(new A(xx, yy, a.step + 1));
map[xx][yy] = a.step + 1;
}
}
}
map[n][n] = 0;
long sum = 0L;
for (int[] ints : map) {
for (int anInt : ints) {
sum += anInt;
}
}
BigDecimal bigDecimal = new BigDecimal(sum);
BigDecimal decimal = new BigDecimal(n * n);
bigDecimal = bigDecimal.divide(decimal, 2, BigDecimal.ROUND_HALF_UP);
System.out.println(bigDecimal);
}
}
class A {
int x;
int y;
int step;
public A(int x, int y, int step) {
this.x = x;
this.y = y;
this.step = step;
}
}
试题F: 小球称重
时间限制: 8.0s 内存限制: 512.0MB 本题总分:15 分
【问题描述】
小蓝有N 个小球,编号1 至N。其中N -1个是正品,重量相同;有1 个是 次品,重量比正品轻。 为了找出次品,小蓝已经用天平进行了M 次称重,并且记录下来每次两边放的小球编号,和称重结果。 请你根据记录,判断还剩下几个小球有次品的嫌疑。
【输入格式】
第一行包含2 个整数N 和M。 以下包含M次称重记录,每个记录占4 行。 第一行是一个整数K,表示天平两边各放了K 个小球。
第二行包含K 个整数,代表放在天平左边的小球编号。
第三行包含K 个整数,代表放在天平右边的小球编号。
第四行是一个字符,为‘>’, ‘<’, ‘=’ 之一。‘>’ 代表左边比右边重,‘<’代 表左边比右边轻,‘=’ 代表两边重量相等。 在一次称重中保证每个小球最多出现1 次。
【输出格式】
输出一个整数,代表答案。
【样例输入】
10 2
3
1 2 3
4 5 6
<
2
3 7
8 9
=’
【样例输出】
2
【样例说明】
{1, 2, 3} < {4, 5, 6} 能判断出次品在{1, 2, 3} 之中。
{3, 7} = {8, 9} 能判断出3 不可能是次品。
所以只剩下{1, 2} 可能是次品。
【评测用例规模与约定】
对于40% 的数据,1 <= N <= 10^6;
对于100% 的数据,1 <= N <= 10^9; 1 <= M <= 10^5, 参与M 次称重的小球总数 < 10^6.
这道题等于代表着两边的小球为正品,大于或小于,代表只要不是轻的天平上的小球,其余全部是正品(这个操作我是备份了一份小球当前正品次品判断状态,然后全部设为正品,再把轻的天平上的小球备份的状态复制过来,不知道还有没有别的操作办法)。
import java.util.Arrays;
import java.util.Scanner;
public class Main6 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String ss = sc.nextLine();
String[] s = ss.split(" ");
int n = Integer.parseInt(s[0]);
int m = Integer.parseInt(s[1]);
boolean[] map = new boolean[1000000010];
int k;
String[] a, b;
for (int i = 0; i < m; i++) {
ss = sc.nextLine();
k = Integer.parseInt(ss);
ss = sc.nextLine();
a = ss.split(" ");
ss = sc.nextLine();
b = ss.split(" ");
ss = sc.nextLine();
switch (ss) {
case ">":
j2(b, map);
break;
case "<":
j2(a, map);
break;
case "=":
j(a, map);
j(b, map);
break;
}
}
long sum = 0;
for (int i = 1; i <= n; i++) {
if (!map[i])
sum++;
}
System.out.println(sum);
}
public static void j(String[] s, boolean[] map) {
for (String s1 : s) {
map[Integer.parseInt(s1)] = true;
}
}
public static void j2(String[] s, boolean[] map) {
boolean[] map2 = Arrays.copyOf(map, 1000000010);
Arrays.fill(map, true);
int n;
for (String s1 : s) {
n = Integer.parseInt(s1);
map[n] = map2[n];
}
}
}
试题G: 背包与魔法
时间限制: 3.0s 内存限制: 1.0GB 本题总分:20 分
【问题描述】
小蓝面前有N 件物品,其中第i件重量是Wi,价值是Vi。她还有一个背 包,最大承重是M。 小蓝想知道在背包称重范围内,她最多能装总价值多少的物品?
特别值得一提的是,小蓝可以使用一个魔法,将一件物品的重量增加K, 同时价值翻倍。(当然小蓝也可以不使用魔法)
【输入格式】
第一行包含3个整数N、M 和K。 以下N 行,每行两个整数Wi 和Vi。
【输出格式】
一个整数代表答案。
【样例输入】
3 10 3
5 10
4 9
3 8
【样例输出】
26
【样例说明】
选择第二件和第三件物品,同时对第二件物品使用魔法。
【评测用例规模与约定】
对于30% 的数据,1 N; M; K 100.
对于100% 的数据,1 N 2000; 1 M; K 10000; 0 Wi; Vi 10000.
dp没有系统的学过,只是知道这个思想,不知道这个用01背包改的对不对。
import java.util.Scanner;
public class Main7 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int bag = sc.nextInt();
int k = sc.nextInt();
int[] v = new int[2010];
int[] w = new int[2010];
for (int i = 1; i <= n; i++) {
w[i] = sc.nextInt();
v[i] = sc.nextInt();
}
int[][][] map = new int[2][n + 1][bag + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= bag; j++) {
// 对第i件使用魔法
if (j >= w[i] + k) {
map[1][i][j] = Math.max(map[1][i][j], map[0][i - 1][j - w[i] - k] + v[i] * 2);
}
// 对第i件不使用魔法
if (j >= w[i]) {
map[0][i][j] = Math.max(map[0][i][j], map[0][i - 1][j - w[i]] + v[i]);
map[1][i][j] = Math.max(map[1][i][j], map[1][i - 1][j - w[i]] + v[i]);
}
}
}
System.out.println(Math.max(map[0][n][bag], map[1][n][bag]));
}
}
试题H: 修路
时间限制: 3.0s 内存限制: 512.0MB 本题总分:20 分
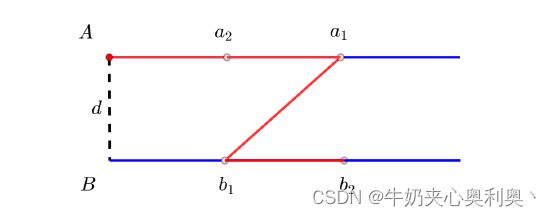
【问题描述】 这天,小明在修路。 他需要修理两条平行的道路A;B,两条路上面分别有n 个和m 个点需要 维修,它们相对于道路起点的距离分别为a1; a2…an 和b1; b2; b…bm。如图, 两条路之间的距离为d 且它们起点(最左端) 的连线和两条路都垂直。小明的起 点为道路A的起点,他需要尽可能快地遍历这些需要维修的n + m 个点,他既 可以沿着道路向右行走,也可以在两条道路之间的空地上随意行走。
小明想知道遍历这些点的最短路程是多少。
【输入格式】
输入共三行,
第一行为三个正整数n;m; d。
第二行为n 个由空格隔开的正整数a1;a2… an。
第三行为m 个由空格隔开的正整数b1; b2… bm。
【输出格式】
一行,一个浮点数,表示答案,保留两位小数。
【样例输入】
2 2 2
2 1
1 2
【样例输出】
5.24
【样例说明】
图中红线指出了样例的最短路线,1 + 1 + 5^(1/2) + 1 = 5.24。
【评测用例规模与约定】
对于30% 的数据,保证n + m 10;
对于100% 的数据,保证n;m 2000; d 4 106; ai; bi 106 。
试题I: 围栏
时间限制: 3.0s 内存限制: 512.0MB 本题总分:25 分
【问题描述】 这天,小明在造围栏。 他提前在地上(二维平面) 打好了n个洞,这n 个洞的位置形成了一个凸多 边形。当他准备把固定围栏的木杆插进去的时候,突然发现自己少准备了两根 木杆。
如图,他现在只能在这n个洞中选出n - 2 个来放置木杆,他想知道用这 n - 2 个木杆能围成的凸多边形的最大的面积是多少。
【输入格式】
输入共n + 1 行,第一行为一个正整数n。 后面n 行,每行两个整数xi; yi 表示第i 个洞的坐标。 保证按照逆时针的顺序输入这n 个点的坐标。
【输出格式】
一行,一个正整数,表示答案。 为了避免小数,请输出面积的两倍。
【样例输入】
5
0 0
1 0
2 1
0 3
-1 1
【样例输出】
6
【样例说明】
选择(-1; 1)(2; 1)(0; 3) 这三个点构成的多边形面积最大,为3,所以输出 6。
【评测用例规模与约定】
对于100% 的数据,保证5 n 100;jxij; jyij 106。
试题J: 好数之和
时间限制: 3.0s 内存限制: 512.0MB 本题总分:25 分
【问题描述】
一个整数如果包含连续的2022四个数字,我们就称之为“好数”。 例如2022、52022、20223、7020224 都是好数,而2202、20022、2222 都不是好数。 给定L 和R,请你计算在L 到R 之间(包含L 和R)所有好数的和是多 少?
【输入格式】
两个整数L 和R。
【输出格式】
一个整数代表答案。
【样例输入】
1 20000
【样例输出】
14044
【样例说明】
满足条件的好数有2022、12022,它们的和是14044。
【评测用例规模与约定】
对于60% 的评测用例,R - L < 10^8
对于100% 的评测用例,1 <= L <= R <= 10^9