智能优化算法:平衡优化器算法 -附代码
2020智能优化算法:平衡优化器算法
文章目录
- 2020智能优化算法:平衡优化器算法
-
- 1.算法背景
- 2.算法优化原理
- 3.实验结果
- 4.参考文献
- 5.Matlab代码
- 6.Python代码
摘要:平衡优化器(equilibrium optimizer, EO)是于2020年提出的一种全新的基于控制容积质量平衡物理现象启发的优化算法。具有寻优能力强,收敛速度快的特点。
1.算法背景
平衡优化器(equilibrium optimizer, EO) 主要是受控制容积强混合型动态质量平衡的物理启发式优化算法。质量平衡方程体现了控制容积内质量进入、离开及生成的物理过程,一般采用一阶微分方程来描述,如下:
V d C d t = Q C e q − Q C + G (1) V\frac{dC}{dt} = QC_{eq} - QC + G \tag{1} VdtdC=QCeq−QC+G(1)
式中 V V V 为控制容积; C C C 为控制容积内的浓度; Q Q Q 为流进或流出控制容积的容量流率; C e q C_{eq} Ceq表示控制容积内部在无质量生成(即平衡状态下)时的浓度; G G G 为控制容积内部的质量生成速率。
通过求解式(1)描述的微分方程,可求得:
C = C e q + ( C 0 − C e q ) F + G ( 1 − F ) / λ V (2) C =C_{eq}+(C_0-C_{eq})F + G(1-F)/\lambda V \tag{2} C=Ceq+(C0−Ceq)F+G(1−F)/λV(2)
F = e x p ( − λ ( t − t 0 ) ) (3) F = exp(-\lambda(t-t_0))\tag{3} F=exp(−λ(t−t0))(3)
式中 F F F为指数项系数; λ \lambda λ 为流动率; C 0 C_0 C0 为控制容积在时间 t 0 t_0 t0的初始浓度。
2.算法优化原理
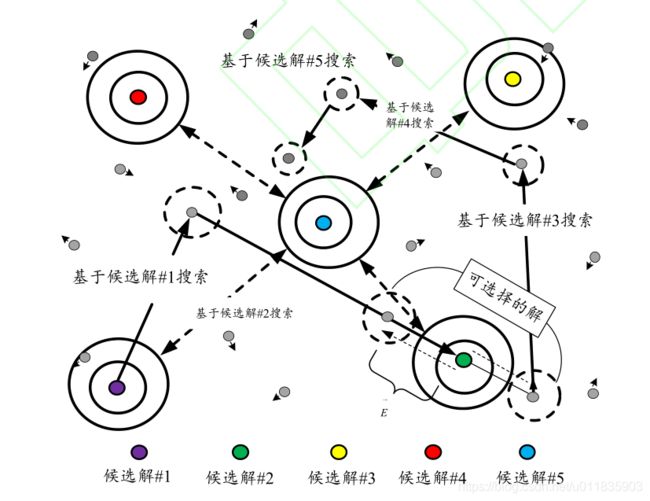
平衡优化器主要基于式(2)展开迭代寻优。对于一个优化问题,等式左边的浓度 C C C 代表新产生的当前解; C 0 C_0 C0代表上一次迭代得到的解; C e q C_{eq} Ceq 代表算法当前找到的最好的解。类似经典 PSO 算法速度更新方程,这里的浓度即代表个体的解,解的更新包括了当前最优解附近的局部搜索和寻优空间内的全局随机搜索,如图 1所示。为满足不同问题的优化需求,算法对具体的操作过程及参数设计如下:
- 初始化:算法在每个优化变量的上下界范围内进行随机初始化,如下:
C i 0 = C m i n + r i ( C m a x − C m i n ) , i = 1 , 2 , . . . , n (4) C_i^0 = C_{min}+r_i(C_{max}-C_{min}),i=1,2,...,n \tag{4} Ci0=Cmin+ri(Cmax−Cmin),i=1,2,...,n(4)
式中 C m i n , C m a x C_{min},C_{max} Cmin,Cmax分别为优化变量的下限和上限向量; r i r_i ri代表个体 i 的随机数向量,其维度跟优化空间维度一致,每个元素值均为 0 至 1 的随机数。
2)平衡状态池:为提高算法的全局搜索能力,避免陷入低质量的局部最优解,式(2)中的平衡状态(即最优个体)将从 5 个当前最优的候选解里面选择(见图 1),这些候选解构成的平衡状态池如下:
C e q , p o o l = { C e q , 1 , C e q , 2 , C e q , 3 , C e q , 4 , C e q , a v e } (5) C_{eq,pool}=\{C_{eq,1},C_{eq,2},C_{eq,3},C_{eq,4},C_{eq,ave}\} \tag{5} Ceq,pool={Ceq,1,Ceq,2,Ceq,3,Ceq,4,Ceq,ave}(5)
式中 C e q , 1 , C e q , 2 , C e q , 3 , C e q , 4 C_{eq,1},C_{eq,2},C_{eq,3},C_{eq,4} Ceq,1,Ceq,2,Ceq,3,Ceq,4分别为截止当前迭代找到的最好的四个解; C e q , 4 C_{eq,4} Ceq,4代表这四个解的平均状态。值得注意的是,这 5 个候选解被选择的概率是一样的,均为 0.2。
-
指数项系数 F:为更好平衡算法的局部搜索和全局搜索,式(3)改进如下:
F = a 1 ∗ s i g n ( r − 0.5 ) [ e − λ t − 1 ] (6) F = a_1*sign(r-0.5)[e^{-\lambda t}-1]\tag{6} F=a1∗sign(r−0.5)[e−λt−1](6)
式中 a 1 a_1 a1为全局搜索的权重常系数; s i g n sign sign 为符号函数; r , λ r,\lambda r,λ 均代表随机数向量,其维度跟优化空间维度一致,每个元素值均为 0 至 1 的随机数。 -
质量生成速率 G :为加强算法的局部寻优能力,生成速率设计如下:
G = G C P ( C e q − λ C ) (7) G = G_{CP}(C_{eq}-\lambda C)\tag{7} G=GCP(Ceq−λC)(7)
G C P = { 0.5 r i , i f r 2 ≥ 0.5 0 , o t h e r w i s e (8) G_{CP}=\begin{cases} 0.5r_i,if\,r_2\geq 0.5\\ 0,otherwise \end{cases}\tag{8} GCP={0.5ri,ifr2≥0.50,otherwise(8)
式中 G C P G_{CP} GCP为生成速率控制参数向量; r 1 r_1 r1为随机数向量,其维度跟优化空间维度一致,每个元素值均为 0 至 1 的随机数; r 2 r_2 r2为 0 至 1 范围内的随机数。
- 解更新:针对优化问题来说,基于式(2),个体的解可更新如下:
C = C e q + ( C − C e q ) F + G ( 1 − F ) / λ V (9) C = C_{eq}+(C-C_{eq})F+G(1-F)/\lambda V \tag{9} C=Ceq+(C−Ceq)F+G(1−F)/λV(9)
算法流程:
Step1.初始化算法参数
Step2.计算适应度值
Step3.根据式(5)确定当前平衡池状态。
Step4.根据式(6)更新指数项系数。
Step5.根据式(7)(8)更新质量生成系数
Step6.根据式(9)更新个体当前解
step7.判断是否满足停止条件,如果满足则输出最终结果,否则重复Step2-Step6。
3.实验结果
4.参考文献
[1]杨蕾,李胜男,黄伟,张丹,杨博,张孝顺.基于平衡优化器的含高比例风光新能源电网无功优化[J/OL].电力系统及其自动化学报:1-9[2020-12-18].https://doi.org/10.19635/j.cnki.csu-epsa.000555.
[1]Afshin Faramarzi,Mohammad Heidarinejad,Brent Stephens,Seyedali Mirjalili. Equilibrium optimizer: A novel optimization algorithm[J]. Knowledge-Based Systems,2020,191.
5.Matlab代码
6.Python代码
上述代码见个人资料介绍
