基于均衡优化算法的无线传感器网络三维覆盖优化
文章目录
- 一、理论基础
-
- 1、种群初始化
- 2、均衡池
- 3、浓度更新
- 4、EO算法伪代码
- 二、仿真实验与分析
-
- 1、函数测试与数值分析
- 2、WSN三维覆盖优化
- 三、参考文献
一、理论基础
均衡优化(Equilibrium Optimizer, EO)算法是Faramarzia等人2019年提出的一种新型启发式算法，其原理是控制体积-质量平衡模型中，粒子根据均衡候选解进行浓度更新，最终达到平衡状态，主要为种群初始化、均衡池及浓度更新三个阶段。
1、种群初始化
与大多数元启发是算法一样，标准EO算法采用随机方式生成初始种群： C → i = L B + R i ⋅ ( U B − L B ) (1) \overrightarrow{C}_i=LB+R_i\cdot(UB-LB)\tag{1} Ci=LB+Ri⋅(UB−LB)(1)其中， C → i \overrightarrow C_i Ci表示初始种群中第 i i i个粒子的初始位置， M M M为种群规模， R i R_i Ri是 [ 0 , 1 ] [0,1] [0,1]的随机向量， i = 1 , 2 , ⋯ , M i=1,2,\cdots,M i=1,2,⋯,M， U B UB UB和 L B LB LB分别是搜索空间的上界和下界。
2、均衡池
种群完成初始化后，粒子缺少达到平衡状态的依据。因此，计算种群中每个粒子适应度值，并根据适应度值的大小得到四个候选解 C → e q _ 1 ∼ C → e q _ 4 \overrightarrow C_{eq\_1}\sim \overrightarrow C_{eq\_4} Ceq_1∼Ceq_4，再由这些候选解求得平均候选解 C → e q _ a v e \overrightarrow C_{eq\_ave} Ceq_ave，五个候选解一起构成均衡池 C → p \overrightarrow C _p Cp。最后，在均衡池中随机选择一个候选解为种群提供判断平衡状态的依据，并参与粒子的浓度更新过程。 C → p = { C → e q _ 1 ∼ C → e q _ 4 , C → e q _ a v e } (2) \overrightarrow C_p=\{\overrightarrow C_{eq\_1}\sim\overrightarrow C_{eq\_4},\overrightarrow C_{eq\_ave}\}\tag{2} Cp={Ceq_1∼Ceq_4,Ceq_ave}(2) C → e q = R a n d ( C → p ) (3) \overrightarrow C_{eq}=Rand(\overrightarrow C_p)\tag{3} Ceq=Rand(Cp)(3)其中， C → e q \overrightarrow C_{eq} Ceq表示以相同概率从均衡池中随机选出的候选解。
3、浓度更新
浓度更新是粒子由当前位置向另一个位置进行寻优的体现，公式如下： C → = C → e q + ( C → − C → e q ) F → + G → λ → V ( 1 − F → ) (4) \overrightarrow C=\overrightarrow C_{eq}+(\overrightarrow C-\overrightarrow C_{eq})\overrightarrow F+\frac{\overrightarrow G}{\overrightarrow\lambda V}(1-\overrightarrow F)\tag{4} C=Ceq+(C−Ceq)F+λVG(1−F)(4)其中， C → \overrightarrow C C表示当前粒子， λ → \overrightarrow\lambda λ是 [ 0 , 1 ] [0,1] [0,1]之间的随机向量， V V V是单位体积， F → \overrightarrow F F为指数项主要用于平衡勘探与开发， G → \overrightarrow G G是生成率被用来提升开发能力。 F → \overrightarrow F F定义如下： F → = a 1 s i g n ( r → − 0.5 ) [ e − λ → t − 1 ] (5) \overrightarrow F=a_1sign(\overrightarrow r-0.5)\left[e^{-\overrightarrow\lambda t}-1\right]\tag{5} F=a1sign(r−0.5)[e−λt−1](5) t = ( 1 − I t e r M a x _ i t e r ) a 2 I t e r M a x _ i t e r (6) t=\left(1-\frac{Iter}{Max\_iter}\right)^{a_2\frac{Iter}{Max\_iter}}\tag{6} t=(1−Max_iterIter)a2Max_iterIter(6)其中， a 1 a_1 a1为常数被用来加速探索或开发，符号函数项 s i g n ( r → − 0.5 ) sign(\overrightarrow r-0.5) sign(r−0.5)用于控制探索或开发的方向， t t t是随着迭代增加而减小一个非线性因子， a 2 a_2 a2用来控制开发能力的常数。 G → \overrightarrow G G定义如下： G → = G → 0 e − λ → ( t − t 0 ) (7) \overrightarrow G=\overrightarrow G_0e^{-\overrightarrow\lambda(t-t_0)}\tag{7} G=G0e−λ(t−t0)(7) t → 0 = 1 λ → ln ( − a 1 s i g n ( r → − 0.5 ) [ 1 − e − λ → t ] ) + t (8) \overrightarrow t_0=\frac1{\overrightarrow\lambda}\ln(-a_1sign(\overrightarrow r-0.5)[1-e^{-\overrightarrow \lambda t}])+t\tag{8} t0=λ1ln(−a1sign(r−0.5)[1−e−λt])+t(8) G → 0 = G C P → ( C → e q − λ → C → ) (9) \overrightarrow G_0=\overrightarrow{GCP}(\overrightarrow C_{eq}-\overrightarrow\lambda\overrightarrow C)\tag{9} G0=GCP(Ceq−λC)(9) G C P → = { 0.5 r 1 r 2 ≥ G P 0 r 2 < G P (10) \overrightarrow{GCP}=\begin{dcases}0.5r_1\quad r_2\geq GP\\0\quad\quad\,\,\,\, r_2
4、EO算法伪代码
EO算法伪代码如图1所示。
二、仿真实验与分析
1、函数测试与数值分析
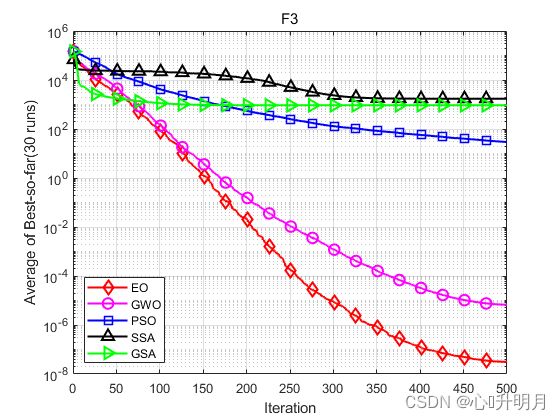
将EO与GWO、PSO、SSA和GSA进行对比，以文献[1]中的F2、F3(单峰函数/30维)、F8、F9(多峰函数/30维)、F18、F19(固定维度多峰函数/2维、3维)为例，种群规模设置为30，最大迭代次数设置为500，每个算法独立运算30次。结果显示如下：
函数：F2
EO：最差值: 6.9804e-22, 最优值: 5.0413e-24, 平均值: 7.8681e-23, 标准差: 1.2846e-22, 秩和检验: 1
GWO：最差值: 6.7034e-15, 最优值: 2.8475e-16, 平均值: 1.617e-15, 标准差: 1.4644e-15, 秩和检验: 3.0199e-11
PSO：最差值: 38557823.6803, 最优值: 51.7484, 平均值: 1285582.5201, 标准差: 7039602.5091, 秩和检验: 3.0199e-11
SSA：最差值: 3.785572212252239e+19, 最优值: 255.4632, 平均值: 1.801053368614618e+18, 标准差: 7.254832697712835e+18, 秩和检验: 3.0199e-11
GSA：最差值: 292.3582, 最优值: 105.4961, 平均值: 199.3335, 标准差: 38.3533, 秩和检验: 3.0199e-11
函数：F3
EO：最差值: 8.6223e-07, 最优值: 8.9116e-15, 平均值: 3.1466e-08, 标准差: 1.5732e-07, 秩和检验: 1
GWO：最差值: 5.8449e-05, 最优值: 8.3805e-09, 平均值: 6.7458e-06, 标准差: 1.3905e-05, 秩和检验: 1.0937e-10
PSO：最差值: 65.1303, 最优值: 12.5415, 平均值: 29.3898, 标准差: 13.4554, 秩和检验: 3.0199e-11
SSA：最差值: 4972.8619, 最优值: 461.0139, 平均值: 1718.2239, 标准差: 1037.0772, 秩和检验: 3.0199e-11
GSA：最差值: 2349.8397, 最优值: 454.9593, 平均值: 927.0963, 标准差: 438.6813, 秩和检验: 3.0199e-11
函数：F8
EO：最差值: -7683.1737, 最优值: -10064.2469, 平均值: -9005.8432, 标准差: 563.6799, 秩和检验: 1
GWO：最差值: -4812.3152, 最优值: -7980.6342, 平均值: -6144.041, 标准差: 777.1093, 秩和检验: 3.3384e-11
PSO：最差值: -2483.5038, 最优值: -4339.0005, 平均值: -3169.5558, 标准差: 412.2052, 秩和检验: 3.0199e-11
SSA：最差值: -4447.2049, 最优值: -9071.1191, 平均值: -7339.6934, 标准差: 868.2064, 秩和检验: 7.3803e-10
GSA：最差值: -1641.8023, 最优值: -3552.5105, 平均值: -2601.5628, 标准差: 458.0927, 秩和检验: 3.0199e-11
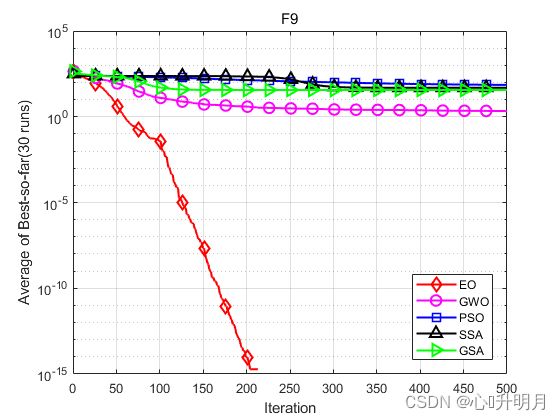
函数：F9
EO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
GWO：最差值: 6.9671, 最优值: 5.6843e-14, 平均值: 2.144, 标准差: 2.5254, 秩和检验: 1.1747e-12
PSO：最差值: 113.3229, 最优值: 47.5237, 平均值: 71.9033, 标准差: 16.861, 秩和检验: 1.2118e-12
SSA：最差值: 79.5965, 最优值: 13.9294, 平均值: 49.4162, 标准差: 18.6731, 秩和检验: 1.2118e-12
GSA：最差值: 57.7075, 最优值: 17.9093, 平均值: 36.5481, 标准差: 8.8682, 秩和检验: 1.2108e-12
函数：F18
EO：最差值: 3, 最优值: 3, 平均值: 3, 标准差: 1.639e-15, 秩和检验: 1
GWO：最差值: 3.0003, 最优值: 3, 平均值: 3, 标准差: 6.4571e-05, 秩和检验: 2.6437e-11
PSO：最差值: 3, 最优值: 3, 平均值: 3, 标准差: 9.231e-14, 秩和检验: 3.3234e-10
SSA：最差值: 3, 最优值: 3, 平均值: 3, 标准差: 2.0292e-13, 秩和检验: 2.6437e-11
GSA：最差值: 3, 最优值: 3, 平均值: 3, 标准差: 4.643e-15, 秩和检验: 6.0521e-09
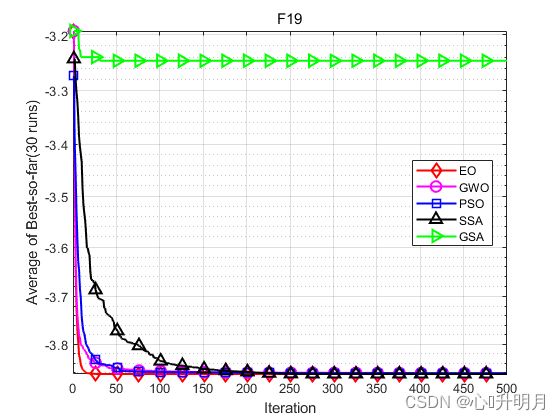
函数：F19
EO：最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 2.5094e-15, 秩和检验: 1
GWO：最差值: -3.8549, 最优值: -3.8628, 平均值: -3.861, 标准差: 0.0028851, 秩和检验: 1.4488e-11
PSO：最差值: -3.8549, 最优值: -3.8628, 平均值: -3.8609, 标准差: 0.0033905, 秩和检验: 9.3879e-11
SSA：最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 7.2714e-11, 秩和检验: 1.4479e-11
GSA：最差值: -2.4836, 最优值: -3.7908, 平均值: -3.2465, 标准差: 0.39077, 秩和检验: 1.4488e-11
结果表明，EO算法能够在探索、开发、避免局部最优和收敛速度方面得到很好的结果。
2、WSN三维覆盖优化
节点覆盖模型请参考这里。设监测区域为 50 m × 50 m × 50 m 50m\times50m\times50m 50m×50m×50m的三维空间，传感器节点个数 N = 30 N=30 N=30，其感知半径是 R s = 10 m R_s=10m Rs=10m，通信半径 R c = 20 m R_c=20m Rc=20m，迭代500次。初始部署、EO优化覆盖、EO算法覆盖率进化曲线如下图所示。
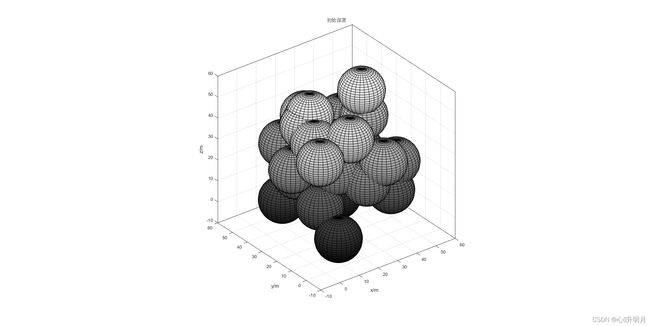
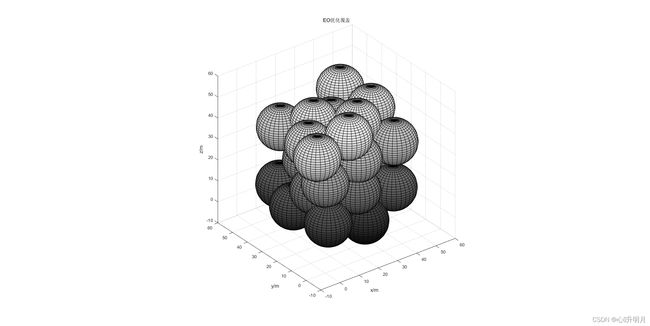
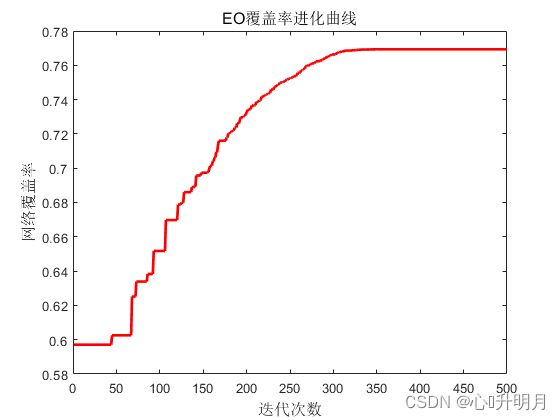初始部署和最终部署的节点位置及对应的覆盖率分别为：
初始位置：
24.524 26.2347 31.1208
2.524 25.5969 26.7119
18.9593 39.1204 40.8974
23.1354 44.542 29.8492
29.8359 30.6764 2.6927
38.4317 44.9749 6.6138
44.9054 32.2333 34.7072
17.1547 14.8717 25.6954
20.1314 9.4267 42.4887
34.6239 40.6145 3.0825
25.8432 5.6055 21.6546
43.2019 8.2044 24.5987
41.2205 43.2299 22.0757
31.1145 0.94774 31.647
49.2216 20.62 13.7732
15.001 30.2088 46.4141
9.505 3.4679 1.4964
23.5328 41.1713 28.2294
44.2009 47.3956 27.16
39.7723 7.3657 12.3704
25.861 23.047 21.3715
9.2631 15.7179 11.3986
1.9202 6.0643 39.283
7.676 29.5334 20.4099
13.3061 46.372 25.9747
10.0104 20.737 39.3712
42.5622 30.9313 48.1584
49.5114 40.4257 12.1062
11.6842 29.9051 42.3906
7.2078 38.6498 4.8618
初始覆盖率：0.59711
最优位置：
44.1264 26.544 41.3813
7.5805 21.31 39.1636
41.3481 43.7681 43.5499
24.4488 43.5488 24.4984
25.9121 42.2361 3.9168
37.2059 32.1599 18.259
45.3993 20.7955 23.387
22.9219 7.5771 33.143
26.3152 7.3486 2.6011
43.1804 38.727 5.4407
40.9222 21.8337 5.6856
22.5169 7.774 18.0365
43.5876 41.9522 28.4084
17.5217 6.9175 45.8206
30.6564 18.3117 42.7764
7.6859 8.0607 7.4064
5.9896 7.9042 27.12
22.685 25.2913 8.0288
29.2809 34.0428 36.722
41.3765 7.8054 12.9137
28.7125 20.3091 23.7054
8.5429 19.0793 17.8285
0.57795 6.1729 42.1115
14.214 31.4077 24.8344
9.1436 42.4902 37.0984
4.7126 27.834 7.5712
41.8338 7.7957 34.5547
40.8052 46.1566 14.5107
17.078 30.1723 42.4791
9.2062 43.0762 9.5256
最优覆盖率：0.76933
实验结果表明，EO算法能够有效提升三维无线传感器网络中节点部署的覆盖率。
三、参考文献
[1] Afshin Faramarzi, Mohammad Heidarinejad, Brent Stephens, et al. Equilibrium optimizer: A novel optimization algorithm[J]. Knowledge-Based Systems, 2020, 191: 105190.
[2] 李守玉, 何庆, 陈俊. 改进平衡优化器算法的WSN覆盖优化[J]. 计算机应用研究, 2022, 39(4): 1168-1172+1189.