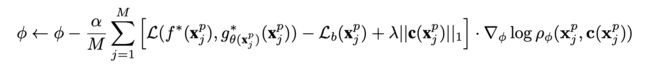Interpretable Rl Summary
文章目录
- Model Approximation Method
-
- Toward Interpretable Deep Reinforcement Learning with Linear Model U-Trees (2018,ECML/PKDD)
-
-
-
- Intro
- contributions
- Model
- Evaluation
-
-
- *Verifiable Reinforcement Learning via Policy Extraction(2018,NeurIPS)
-
-
-
- Intro
- Contributions
- Model
- Evaluation
-
-
- *Towards Interpretable-AI Policies Induction using Evolutionary Nonlinear Decision Trees for Discrete Action Systems (2019)
-
-
-
- Intro
- Model
- Evaluation
-
-
- RL-LIM: Reinforcement Learning-based Locally Interpretable Modeling (2019)
-
-
-
- Intro
- Contributions
- Model
-
-
- Modelling Agent Policies with Interpretable Imitation Learning (2020,TAILOR)
-
-
-
- Intro
- Model
- Evaluation
-
-
- Improved Policy Extraction via Online Q-Value Distillation (2020,IJCNN)
-
-
-
- Intro
- Contributions
- Model
- Evaluation
-
-
- Neural-to-Tree Policy Distillation with Policy Improvement Criterion (2021)
-
-
-
- Intro
- Contributions
- Model
- Evaluation
-
-
- Can You Trust Your Autonomous Car? Interpretable and Verifiably Safe Reinforcement Learning(2021, IEEE Intelligent Vehicles Symposium (IV))
-
-
-
- Intro
- Contributions
- Model
- Evaluation
-
-
- *Explaining by Imitating: Understanding Decisions by Interpretable Policy Learning (ICLR, 2021)
-
-
-
- Intro
- Contributions
-
-
- *POETREE: Interpretable Policy Learning with Adaptive Decision Trees (2022)
-
-
-
- Intro
- **contributions**
- Model
- Evaluation
-
-
- Self-interpretable Modeling Method
-
-
-
- *Distilling a Neural Network Into a Soft Decision Tree (2017,CEx@AIIA)
- *Optimization Methods for Interpretable Differentiable Decision Trees in Reinforcement Learning(2019)
-
- Intro
- Contributions
- Model
- Evaluation
- Conservative Q-Improvement: Reinforcement Learning for an Interpretable Decision-Tree Policy (2019)
-
- Intro
- Contributions
- Model
- Evaluation
-
-
- Post-hoc Interpretation Method
-
- *Programmatically Interpretable Reinforcement Learning (2018, ICML)
- *Explainable Reinforcement Learning Through a Causal Lens (2019, AAAI)
-
-
-
- Intro
- Contributions
- Evaluation
-
-
- *Generation of Policy-Level Explanations for Reinforcement Learning (2019, AAAI)
-
-
-
- Intro
- Contributions
- Model
-
-
- TripleTree: A Versatile Interpretable Representation of Black Box Agents and their Environments(2020,AAAI)
-
-
-
- Intro
- **Key Features**
- Model
- Evaluation
-
-
- Feature-Based Interpretable Reinforcement Learning based on State-Transition Models (2021,IEEE)
-
-
-
- Intro
- Method Propertity
- Model
- Evaluation
-
-
- *EDGE: Explaining Deep Reinforcement Learning Policies (2021, NeuralPS)
-
-
-
- Intro
- Contributions
- Model
- Posterior Inference and Parameter Learning
- Evaluation
-
-
*代表重要文章
Model Approximation Method
这种方法一般可以分类为策略蒸馏和模仿学习(这两类其实差不多),都关注于如何用一个可解释的模型,去逼近以及解释DRL中的黑盒代表的映射函数。针对于模仿学习中的distributional shift 问题,其中VIPER利用了DAgger,而LMUT利用了进化算法,都能取得和DRL相似的performance 并且决策树的规模不会太大。
Toward Interpretable Deep Reinforcement Learning with Linear Model U-Trees (2018,ECML/PKDD)
Intro
这篇文章和我们做的方向一致。是第一篇讲强化学习和模仿学习结合的文章,通过LMUT模仿学习Q值。但并没有解决distrubution drift的问题并且在cartpole上的表现一般。
contributions
- To our best knowledge, the first work that extends interpretable mimic learning to Reinforcement Learning.
- A novel on-line learning algorithm for LMUT, a novel model tree to mimic a DRL model.
- We show how to interpret a DRL model by analyzing the knowledge stored in the tree structure of LMUT.
Model
文章提出了两种生成数据(用于监督学习)的方式:
**Experience Training:**记录所有在DRL训练时产生的状态和动作(这个优点是状态会比较符合环境中的分布,但缺点是很多动作并不是最优值因为会导致训练效果不好)。

**Active Play:**通过一个训练好的模型与环境交互生成数据(优点是动作都是最优,确实的状态的分布是偏移的)。
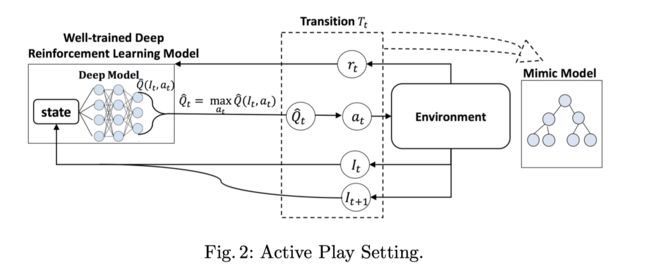
Linear Model U-Trees
可以用于回归问题,每个叶子结点是一个线性模型。LMUT同时也记录reward r r r和状态转移概率 p p p
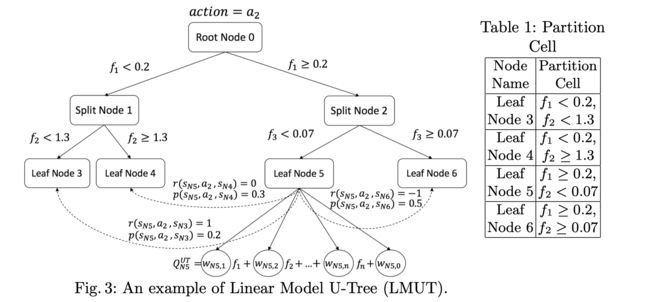
整个训练分为两个阶段
Data Gathering Phase: 收集transitions用于拟合线性模型和分裂结点。
Node Splitting Phase:
LMUT扫描所有的叶子结点并且利用SGD更新线性模型,如果SGD的提升不明显,则分裂该结点。对一个batch的数据,每个叶子结点只考虑一次分裂。

SGD weight update
对每个动作都建立一棵LMUT。
Q U T ( I t ∣ w N , a t ) = ∑ j = 1 J I t j w N j + w N 0 Q^{UT}(I_t| w_N, a_t) = ∑_{j=1}^J I_{tj}w_{Nj}+ w_{N0} QUT(It∣wN,at)=∑j=1JItjwNj+wN0

**splitting criterion: **Variance test-选择一个分裂使得孩子结点上的Q值分布方差最小
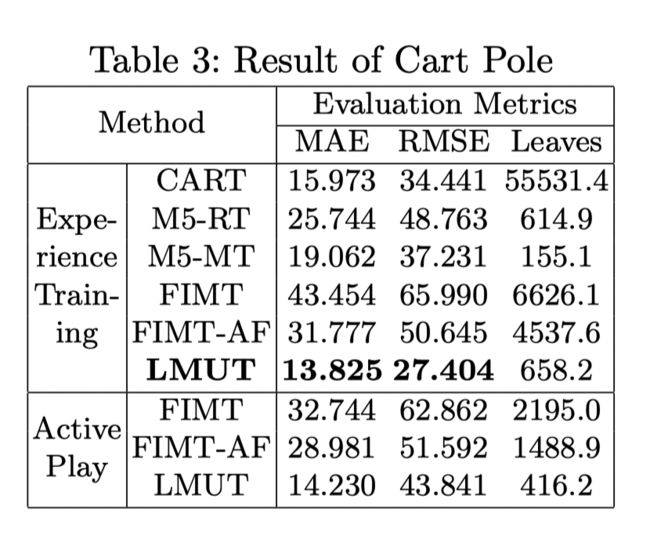
Evaluation

*Verifiable Reinforcement Learning via Policy Extraction(2018,NeurIPS)
Intro
将一个表现好的DRL策略蒸馏或提取到决策树策略中。基于模仿学习实现并且在生成用于监督学习的标签时结合DAGGER。但考虑到DAGGER生成的决策树过于复杂并且无法利用累积收益(例如Q function)这个信息,因此提出了Q-DAGGER这个算法。并且将其与提取决策树策略相结合得到VIPER。同时文章另一个贡献是提出了何如对决策树进行正确性,鲁棒性,稳定性对验证。
Contributions
- We propose an approach to learning verifiable policies.
- We propose a novel imitation learning algorithm called VIPER, which is based on DAGGER but leverages a Q-function for the oracle. We show that VIPER learns relatively small decision trees (< 1000 nodes) that play perfectly on Atari Pong (with symbolic state space), a toy game based on Pong, and cart-pole.
- We describe how to verify correctness (for the case of a toy game based on Pong), stability, and robustness of decision tree policies, and show that verification is orders of magnitude more scalable than approaches compatible with DNN policies.
Model
Q-DAGGER algorithm
考虑一个非凸的损失函数(可以看优势函数):

让 g ( s , π ) = I [ π ( s ) = π ∗ ( s ) ] g(s, π) = I[π(s) = π^∗ (s)] g(s,π)=I[π(s)=π∗(s)] 为一个0-1损失函数,让$\tilde g(s, \pi) $ 为一个凸上界(例如 hinge loss),则有
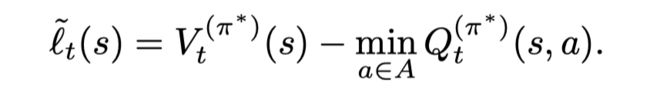
为原始损失函数的一个凸上界。
首先定义损失函数为
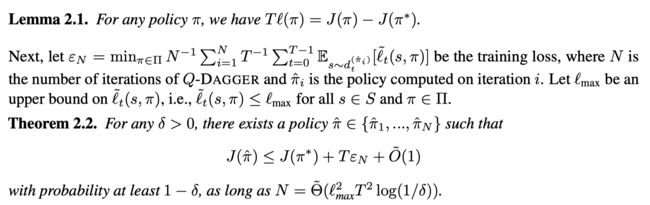
Lemma2.1 就是TRPO,两个策略之间表现的差异可以通过一个优势函数(损失函数)来表示。
Theorem2.2 证明了可以找到一个策略,使得这个策略和最优策略之间的差异有一个上界(这里的 J J J不是衡量reward而是cost)。
Extracting decision tree policies
因为我们使用的损失函数是非凸的,因此不满足DAGGER的要求不能进行online learning。因此文章采用了heuristic based on the follow-the-leader algorithm,在每一次迭代中,利用收集的数据集训练CART决策树。并且我们修改CART的损失函数, CART根据权重 l ~ ( s ) \tilde l(s) l~(s) 对原始数据集数据集进行重新采样。则根据
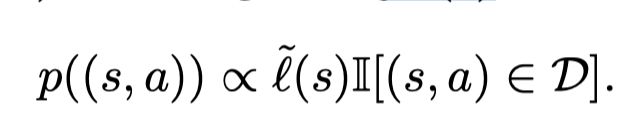
因此我们有 E ( s , a ) ∼ p ( ( s , a ) ) [ g ~ ( s , π ) ] = E ( s , a ) ∼ D [ l ~ ( s , π ) ] E_{(s,a)∼p((s,a))}[\tilde g(s, π)] = E_{(s,a)∼D}[\tilde l (s, π)] E(s,a)∼p((s,a))[g~(s,π)]=E(s,a)∼D[l~(s,π)], 则我们在重新采样的数据集中训练决策树等价于在原始数据集中根据损失函数训练决策树。

Correctness for toy Pong
针对这个游戏的正确性指的是我们通过系统动态和我们的模型证明我们的策略不会输掉游戏(不是依赖于像神经网络模型通过大量的实验,经验性地估计或证明这是一个正确的策略)。
环境的动态和控制器都是分段线性的,他们的联合动态也是分段线性的。系统动态在t时刻可以表示为:
所以t时刻的状态可以t-1时刻的状态线性表示的集合的并集,则系统的正确性可以表示为:
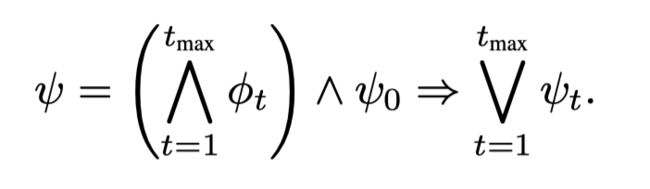
其中 ψ t = ( s t ∈ Y 0 ) ψ_t= (s_t ∈ Y_0) ψt=(st∈Y0), 其中 Y 0 Y_0 Y0是一个初始的安全区域, t m a x t_{max} tmax为在一些文章假设下,小球从初识安全区域出发,最多 t m a x t_{max} tmax会再次进入到安全区域中。有标准的工具来验证是否上述式子是否满足,因此我们认为我们的控制器是正确的如果 ψ ψ ψ不被满足。
Stability
因为涉及了控制方面的理论我没有看
Robustness
鲁棒性在图像分类中被广泛研究。我们说一个策略在 s 0 s_0 s0是 ε − r o b u s t ε-robust ε−robust 如果
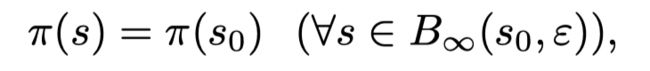
对于决策树,我们可以计算最大的 ε ε ε使得策略是在 s 0 s_0 s0是 ε − r o b u s t ε-robust ε−robust
下面的公式计算了从 s 0 s_0 s0到到最近 s ∈ S s ∈ S s∈S使得 s ∈ r o u t e d ( l ; π ) s ∈ routed(l; π) s∈routed(l;π)。也就是对于每个叶子结点 l l l(该叶子结点的标签和 π ( s 0 ) π(s_0) π(s0)不同),我们计算落在这个叶子结点中的状态中,和 s 0 s_0 s0的最大距离 ε ε ε。
我有两个疑问
- 就是第一个公式为什么是max, 如果是max的话不就每一个ε都是∞
- 并且文章中说 “we can efficiently compute the largest ε ε ε such that π π π is ε − r o b u s t ε-robust ε−robust at s 0 s_0 s0”,那为什么第二个式子是取argmin
Evaluation
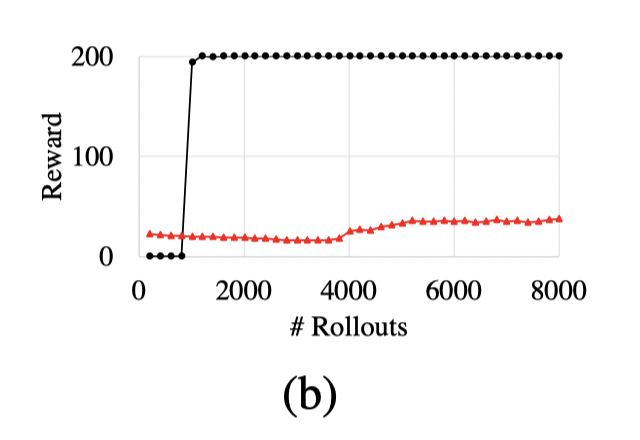
在cartpole问题上和fitted Q iteration比较,一个基于决策树而不是梯度下降的AC方法。
*Towards Interpretable-AI Policies Induction using Evolutionary Nonlinear Decision Trees for Discrete Action Systems (2019)
Intro
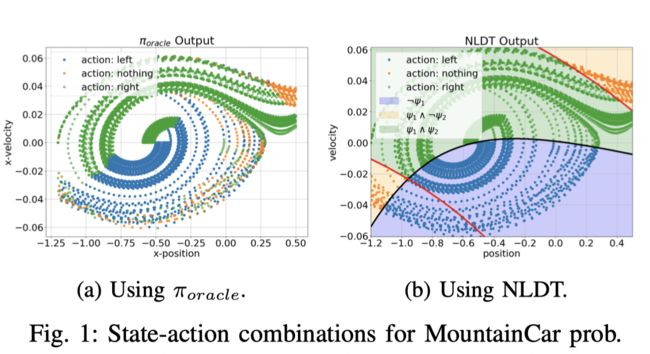
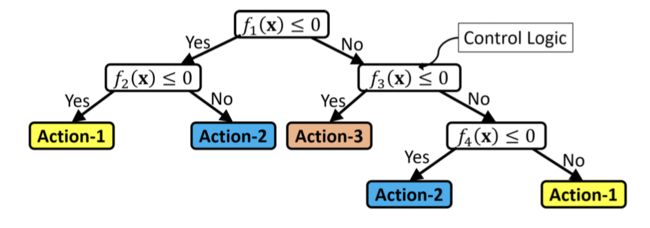
文章基础模仿学习的框架,提出了一个非线性的决策树和一个基于进化算法的二次训练框架使得决策树的复杂度降低同时保留好的模型性能。在训练后的决策树易于解释并且实际的效果也很好。通过动作对线性空间的划分,文章尝试用一些的特征的非线性组合来完成对动作空间的划分。如下图所示,通过三个动作,策略可以简单定义为:
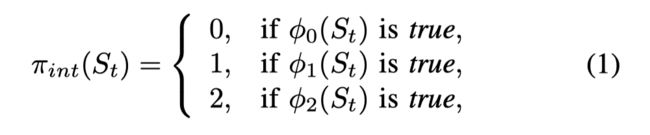
其中的 ϕ i \phi_i ϕi是一个布尔函数,文章给出了具体的非线形组合:

可以看出在这个问题,文章给出的可解释策略非常简单易懂,具有极强的可解释性。
Model
Nonlinear Decision Tree (NLDT)
每个结点都有一个非线性的函数,并且可以有两个孩子结点。每个结点的分裂规则 f ( x ) f(x) f(x)定义如下:

其中 B i = ∏ j = 1 d x j b i j B_i= ∏_{j=1}^dx_j^{b_{ij}} Bi=∏j=1dxjbij, m m m是一个indicator
Open-loop Training
可以认为是个预训练阶段,由DRL收集数据并转换为监督学习,使得决策树首先学习一个逼近DRL的策略。
训练决策树采取bilevel optimization algorithm,优化公式为:
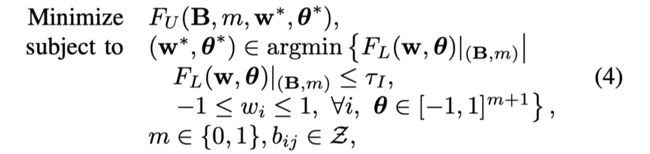

其中 Z Z Z是一个指数集={ −3, −2, −1, 0, 1, 2, 3 }。 F U F_U FU代表了复杂度, F L F_L FL代表了结点纯度,在文章中采用基尼指数。 τ I τ_I τI代表了孩子结点的最大纯,也就是一个终止分裂的条件。
Closed-loop Training
这一阶段训练的目的是为了保证模型的表现,在open-loop训练中,我们只确保了模型是逼近DRL的,在closed-loop中,优化的对象变为了平均episode reward。同时我们也可以用来降低模型的复杂度。在闭环训练中,文章调整并重新优化 N L D T O L NLDT_{OL} NLDTOL或者是剪枝的 N L D T O L P NLDT_{OL}^P NLDTOLP (P代表了保留决策树的前P层),优化公式变为:

文章中没有给到这一步的优化方法,不过考虑到目标函数是average episode reward,可以采用很多启发式算法进行训练。
Evaluation
在cartpole这种小规模问题上,不需要闭环训练就可以有好的结果。
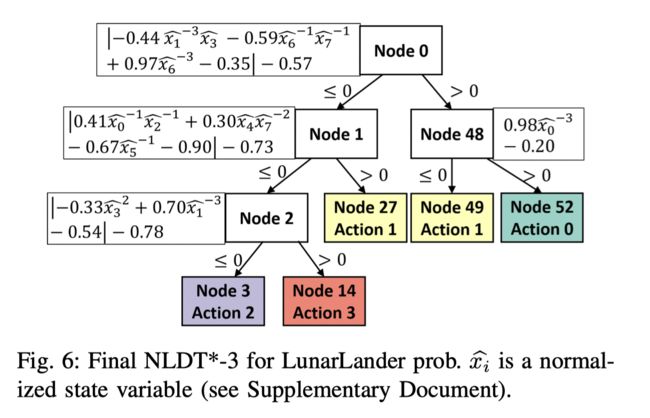
LunarLander Problem
在这个问题上,仅有开环训练的模型实际表现一般,因此要引入闭环训练。
可以看到在闭环训练后,保留四层的NLDT成功解决了问题。并给出了可视图:
RL-LIM: Reinforcement Learning-based Locally Interpretable Modeling (2019)
Intro
文章并没有解释强化学习策略,而是用了一个基于强化学习的思想用来解决局部解释模型representational capacity不足的问题。局部解释也就是不在整个训练集上训练,而是关注于某些最有价值的instances来捕捉深度模型的行为,而用来训练的instances由一个神经网络来选择。目前有挺多关于 locally interpretable modeling 的研究,例如 LIME,SILO,MAPLE。
Contributions
-
We introduce the first method that tackles interpretability through data-weighted training, and show that reinforcement learning is highly effective for end-to-end training of such a model.
-
We show that distillation of a black-box model into a low-capacity interpretable model can be significantly improved by fitting with a small subset of relevant samples that is controlled efficiently by our method.
-
On various classification and regression datasets, we demonstrate that RL-LIM significantly outperforms alternative models (LIME, SILO and MAPLE) in overall prediction performance and fidelity metrics – in most cases, the overall performance of locally interpretable models obtained by RL-LIM is very similar to complex black-box models.
Model
Instance-wise weight estimation mode: h φ : X × X × Y → [ 0 , 1 ] h_φ: X × X × Y → [0, 1] hφ:X×X×Y→[0,1], 一个probe 特征,一个训练特征,一个神经网络在训练特征上的输出。利用一个probe变量去计算一对训练数据的概率。
目标函数为:
目标函数的第一项最小化可解释模型喝深度模型动作选择的差异,第二项控制用来进行训练instances的数量, h ϕ h_{\phi} hϕ 表示一个训练pair的权重。最后一个限制条件限制了可解释模型训练时,训练数据是带权重的。
Training
在stage3, 文章首先训练了一个全局解释模型作为baseline。
则优化目标的第一项变为:
第二项变为:
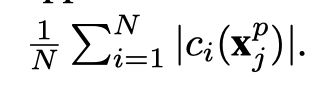
约束项变为:

因为涉及到一个采样操作,因此instance-wise weight estimator无法进行梯度下降更新。因此文章借用了REINFOCE的思想,将loss定为:
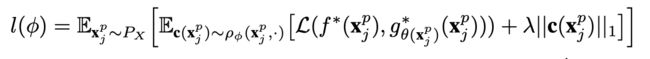
其梯度为:
整体训练流程如下:
Modelling Agent Policies with Interpretable Imitation Learning (2020,TAILOR)
Intro
文章提出了interpretable imitation learning (I2L),但是整体思想比较简单。就是利用传统决策树进行一个模仿学习并且没有加入DAGGER也没有什么提高效率的训练框架。比较值得注意的是文章不仅进行动作的模仿学习,还进行状态表征学习(也比较简单)。
Model
首先问题的定义为:

其中 ϕ ′ \phi' ϕ′为状态表征函数, π \pi π为可解释策略。
Learning Procedure:
- 利用领域知识得到一个特征生成器和递归深度,确定一个状态表征空间 φ a l l φ_{all} φall。
- 利用 ϕ a l l \phi_{all} ϕall和训练好的DRL生成训练数据。
- 基于CART的生成一颗最大的树,这颗树不断拓展直到每个结点都是“纯”的
- 利用CCP进行剪枝操作,得到一个树的序列。
- 从树的序列中选择一个棵树,到这里是模仿学习的部分。将 ϕ a l l \phi_{all} ϕall中至少用过一次的特征提取出来组成 ϕ ′ \phi ' ϕ′,这里是状态表征学习的部分。
Evaluation
在一个交通模拟器上进行实验。实验设置得比较简单并且target policy不是一个神经网络。
Improved Policy Extraction via Online Q-Value Distillation (2020,IJCNN)
Intro
通过BSP tree 对DRL策略进行策略蒸馏,一个训练好的DRL策略在环境中执行动作,所以的transitions经过一个Online的策略蒸馏算法,将信息压缩进一个理想的树结构。
Contributions
- We present a novel data structure we call the Q-BSP tree, to learn distilled reinforcement learning policies. QBSP tree nodes are strictly more expressive than standard decision tree nodes and are effective at capturing pair-wise dependencies among input features.
- We present a new combined regression and ranking algorithm based on the particle Gibbs sampler, which enables the online distillation of deep reinforcement learning policies into Q-BSP trees. We find that this method performs better and is relatively more scalable than previous distillation approaches applied to reinforcement learning policies.
- In addition to the best regression and gameplay performance, the policies distilled by the trees closely resemble the neural network in terms of feature importance. We introduce this as a new effectiveness metric for distillation.
Model
Binary Space Partitioning Tree
每棵树都包含了一系列的内部节点(决策规则)和叶子结点(参数值)。首先为了拓展树结构,一个叶子结点被采样根据 { ∑ d 1 , d 2 P ( d 1 , d 2 ) k } k = 1 b \{ ∑_{d_1,d_2}P^k_{(d_1,d_2)}\}_{k=1}^b {∑d1,d2P(d1,d2)k}k=1b, ( d 1 , d 2 ) (d_1, d_2) (d1,d2) 为任意的两个维度,而 P ( d 1 , d 2 ) k P^k_{(d_1,d_2)} P(d1,d2)k则代表了在叶子结点 k k k上,输入点在 ( d 1 , d 2 ) (d_1, d_2) (d1,d2)两个维度上的投影的边缘(凸包)。一旦一个叶子结点确定被分裂,两个维度 ( d 1 ∗ , d 2 ∗ ) (d^*_1, d_2^*) (d1∗,d2∗)根据投影边缘被采样用于划分一个分割平面。一个角度从 ( 0 , π ] (0, π] (0,π]随机产生,确定了在该平面上的一个线段,一个随机位置 u u u在线段上选取,从而确定一条直接穿过u和投影,垂直于线段的直线(图中红色虚线),从而将一个节点分为两个叶子节点(step4)。最后从一个指数族中采样一个cost, 如果cost超过budget,则拒绝分裂。
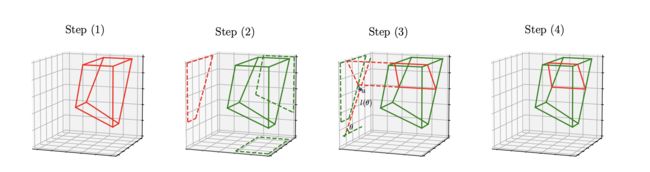

Q-BSP Forest
对每一个动作都建立一棵Q-BSP树组成森林。
对于一棵树,叶子结点 z z z上有参数值 μ z \mu_z μz,我们用一个函数g来包括了一个输入从根节点到叶子结点的传播以及第i个动作Q值的计算。

Online Expansion of Node Partitions
传统的BSP树基于给定的观测点计算凸包,因此并不适用于online的算法。但强化学习通常会有一个复杂的状态空间,因此将其拓展为一个online版本,训练样本为一个输入数据流。我的理解是训练了原始的BSP后,通过与环境的交互会观测到一些新的数据点,因此文章提出一个online的拓展树的算法而不是将新老数据集合并然后重头训练一棵树。。当一个新的样本被观测到时,通常发生只有两种情况:1.一个现存的分割边界被拓展 2.生成一个新的分割。
如果一个新观测的数据,存在当前结点的边界之外,则一个新的凸包(边界)生成。

Distillation Training Process
文章采用一个fixed interval based approach,每个节点会分配一个budget,每个阶段的分割产生的cost的和不能超过这个budget。每个阶段都有对应的一棵的树生成。在有了这些原始的树,文章通过粒子群算法进行优化。每个阶段都有R个突变的树和一个对应i阶段的原始的树,并且通过竞争留下来的冠军克隆R棵树进入下个阶段。突变包括将一个节点进行分裂,将一个节点及其孩子结点都销毁或者什么都不做。评分函数为在训练机上回归准确率的提升。
Evaluation
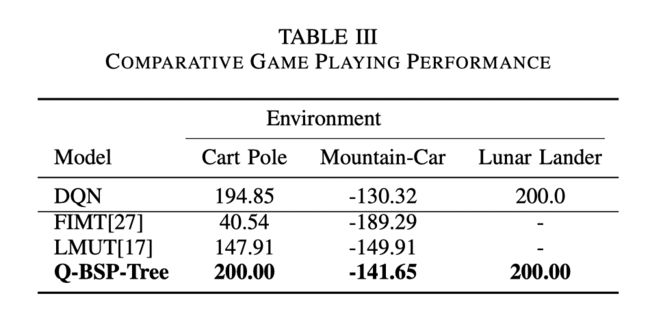

GI=Gini Importance, MDA=Decrease in Accuracy,GI=Integrated Gradients
Neural-to-Tree Policy Distillation with Policy Improvement Criterion (2021)
Intro
文章提出了一个策略蒸馏算法,Dpic,蒸馏的优化目标函数从TRPO策略提升准则中获取,也就是确保新策略是在旧策略上的提升。与模仿学习不同,Dpic可以用与offline学习这样可以控制住online学习时采样数据,数据分布偏移的问题。文章提出了一个CART的修改版,修改了采用gini指数作为分裂标准的方式。
Contributions
- We proposed an advantage-guided neural-to-tree distillation approach, and analysed the connection between the advantage cost and the accumulative rewards of the distilled tree policy
- Two practical neural-to-tree distillation algorithms are devised and tested in several environments, showing that our methods performs well in both the terms of the average return and the consistency of state distribution.
- We investigate the interpretability of the distilled tree policies in the fighting game and the self-driving task, showing that our distilled decision tree policies deliver reasonable explanations.
Model
Decision Node Splitting Criterion
-
Error reduction: 在分裂的时候,选择分裂的特征和对应值最大化误差的减少(通过是在一个独立验证集上的误差)

-
Cost reduction:首先定义一个样本被分类到类别k到cost为 k ∈ Y k ∈ Y k∈Y as C k C_k Ck,类别k在一叶子结点中的cost为 C N k = ∑ D N C k C_N^k= ∑_{D_N} C^k CNk=∑DNCk,则每个叶子结点的总的cost为 W N = ∑ k ∈ Y C N k W_N= ∑_{k∈Y}C_N^k WN=∑k∈YCNk。分裂的准则为最大化cost的减少。
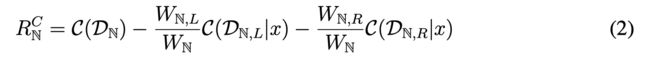
-
但cost reduction的分裂方式存在 node-splitting degradation problem的问题,就是如果每个孩子结点和父结点的标签一样,那 R N C R_N^C RNC就会为0,这样对每个分裂结点的评估都会是一致的(0)。数学上原因为 f ( z ) = m i n { z i } f(z) = min \{ z_i\} f(z)=min{zi}不是严格凸的,也就是 ∃ z ′ , z ′′ , a r g m i n { z i ′ } = a r g m i n { z i ′′ } = a r g m i n { θ z i ′ + ( 1 − θ ) z i ′′ } ∃z^′, z^{′′}, argmin \{ z_i^′\} = argmin \{ z_i{′′}\} = arg min \{ θz_i^′+ (1 − θ)z_i^{′′}\} ∃z′,z′′,argmin{zi′}=argmin{zi′′}=argmin{θzi′+(1−θ)zi′′},则
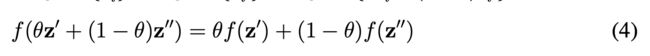
-
因此为了解决这个问题,加入个熵,比如信息熵
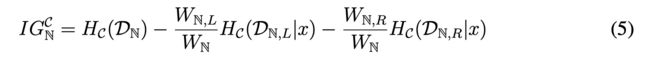
Policy Improvement Criterion
在TRPO中,我们有:
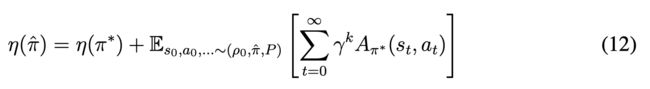
新旧策略之间的表现差异可以通过一个优势函数来表示。通过 ρ π ( s ) = ∑ t = 0 ∞ γ t P ( s t = s ) ρ_π(s) = ∑_{t=0}^∞γ^tP(s_t= s) ρπ(s)=∑t=0∞γtP(st=s), 可以重写为:

Distillation objective
我们用一棵决策树去模仿DRL的策略,则有:
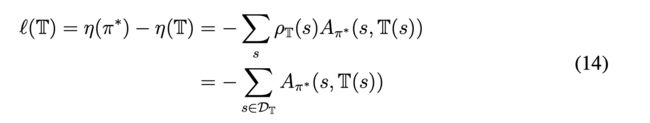
第三个等号我觉得需要除以 ∣ D T ∣ |D_T| ∣DT∣, D T D_T DT是由决策树采样到的数据集。
考虑到一般我们Offline的数据是由于DRL的策略采样得到,则上式可以写成:
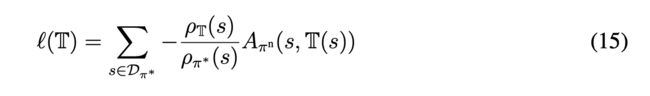
文章认为考虑到决策树没有复杂度的限制(可以变成一棵非常大的树),因此决策树会与DRL的策略相似,因此他们的状态分布会比较相似,可以将目标函数写为:

但我认为这个假设在训练的初期并不成立,直接这样改写会导致在处理的优化目标就是期望有偏的,可能会导致决策树无法学到DRL策略。我认为可以前期用模仿学习的方法,等决策树策略逼近DRL了,再通过文章的方法进一步提升决策树。
有了(16),我们可以将advantage information 作为分类cost (代替info gain 或者基尼指数),通过这种方式不断分裂得到的决策树是不断降低这个损失函数的。
考虑到基于(16)的更新通常会导致树的规模很多,因此为了降低复杂,文章也考虑加入了BC的惩罚项,新的目标函数可以写为:
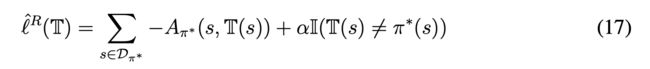
Evaluation
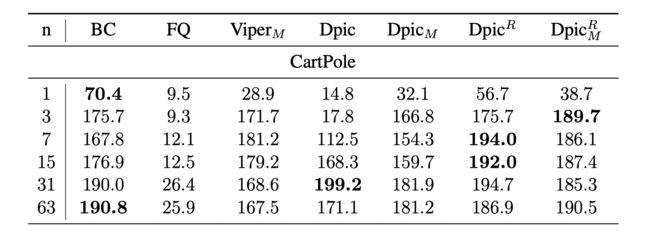
M代表resample,R则是加了惩罚项目,n代表了最大结点数量。
可以看到表现最好的是没有带惩罚项的Dpic。
Can You Trust Your Autonomous Car? Interpretable and Verifiably Safe Reinforcement Learning(2021, IEEE Intelligent Vehicles Symposium (IV))
Intro
这篇文章针对自动驾驶领域,将VIPER的训练框架进行一些修改,将其与 safe reinforcement learning相结合。
Contributions
- This paper provides a pipeline that builds on this technique to create policies that are both safe and interpretable. The pipeline trains a non-interpretable RL agent for safe behavior, modifying existing reward structures and training techniques. It then extracts a set of rules approximating the policy in the form of a decision tree.
- We show that this extracted policy is as performant and safe as the deep neural network (DNN) agent, and at the same time easily interpretable. The last component of our pipeline formally verifies (or rejects)the safety of our trained agents for linearized system dynamics.
- To the best of our knowledge, this presents the first application of VIPER and its verification ideas to an autonomous driving scenario.
Model
Safe Training
添加一个reward项用来进行安全限制:
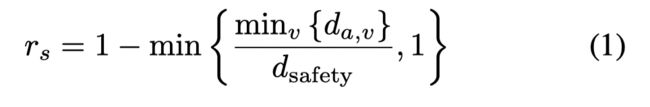
其中 d a , v d_{a,v} da,v是agent和其他车辆的距离, d s a f e t y d_{safety} dsafety是一个理想的安全距离。
Safe Extraction
原始的viper算法并不适用于安全强化学习,从一个safe teacher policy通常会学出unsafe trees,有以下三点原因:
- 首先在VIPER中的采样权重是根据teacher policy的preference并没有考虑限制条件,也就是一些重要的可以避免撞毁的重要决策可能会有较低的权重,因此我们将轨迹(由学生策略生成的)中的steps视为重要的如果满足 1)这个轨迹以违反约束条件结束 2)学生和老师的决策不同。为了使得学生可以更好地从错误中学习,通过这些重要的steps我们得到第二个数据集,并且这个数据集中的样本有更高的权重(文章采用5)。这个修改依赖于老师是一个安全的策略。
- VIPER在训练中没有排除掉一些不安全的学生,文章将那些经常出事的学生排除出训练。
- VIPER算法考虑最小化学生和教师动作选择的差异,因此会产生一棵复杂度较高的树,因此文章限制树的深度。

算法最后返回表现最好的树,并且加上一个违法限制条件的惩罚项。
Evaluation
文章在一个简单的自动驾驶环境上进行实验

*Explaining by Imitating: Understanding Decisions by Interpretable Policy Learning (ICLR, 2021)
Intro
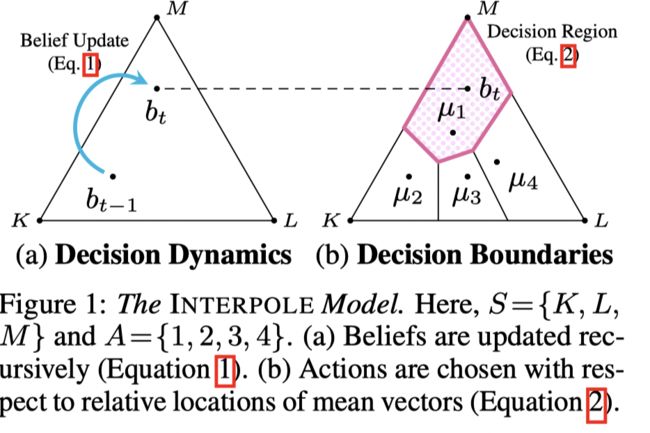
文章提出了一个计算决策动态和决策边界的算法,并且利用EM算法训练模型。
Contributions
-
we propose a model for interpretable policy learning (“I NTERPOLE”)—where sequential observations are aggregated through a decision agent’s decision dynamics (viz. subjective belief-update process), and sequential actions are determined by the agent’s decision boundaries (viz. probabilistic belief-action mapping).
-
we suggest a Bayesian learning algorithm for estimating the model, simultaneously satisfying the key criteria of transparency, partial observability, and offline learning.
-
through experiments on both simulated and real-world data for Alzheimer’s disease diagnosis, we illustrate the potential of our method as an investigative device for auditing, quantifying, and understanding human decision-making behavior.
*POETREE: Interpretable Policy Learning with Adaptive Decision Trees (2022)
Intro
这篇文章提出了一个Offline的学习框架,对记录病人问诊轨迹的医疗数据集学习决策过程,并且在数据集中没有奖励函数,状态空间和状态转移概率。文章利用了soft decision tree并提出了recurrent decision tree, 不仅可以学习策略,还可以用于表征学习和预测病人未来发展。同时基于验证集不断拓展树的拓扑结构并剪枝。
contributions
- A novel framework for policy learning in the form of incrementally grown, probabilistic decision trees, which adapt their complexity to the task at hand
- An interpretable model for representation learning over timeseries called recurrent decision trees.
- Illustrative analyses of our algorithm’s expressive power in disambiguating policies otherwise unidentifiable with related benchmarks; integration of domain knowledge through inductive bias; and formalisation and quantification of abstract behavioural concepts
Model
f f f 为一个表征函数,将病人的历史观测和动作映射到一个表征空间, h t = f ( z 1 , a 1 , . . . z t − 1 , a t − 1 ) = f ( z 1 : t − 1 , a 1 : t − 1 ) ∈ H h_t= f(z_1, a_1, ...z_{t−1}, a_{t−1}) = f(z_{1:t−1}, a_{1:t−1}) ∈ H ht=f(z1,a1,...zt−1,at−1)=f(z1:t−1,a1:t−1)∈H,则按照POMDP的定义, { h t , z t } \{ h_t, z_t\} {ht,zt}组成了状态 s t s_t st的belief,与POMDP的策略学习不同(从belif映射到动作空间),为了可解释性,文章关注于从状态到动作空间的映射。
adaptive decision-making policy的定义为 π : Z × H × A → [ 0 , 1 ] π : Z × H × A → [0, 1] π:Z×H×A→[0,1]
Soft Decision Tree
每个inner node都有一个gating function: p g a t e n ( x ) = σ ( x T w n + b n ) p_{gate}^n(x) = σ ( x^Tw^n+ b^n) pgaten(x)=σ(xTwn+bn), 为了提供更好地解释性,同样可以保留权重中最大的一部分来组成一个轴对称的决策来或者将权重变得稀疏。从根节点到叶子结点的路径概率 P n ( x ) P^ n(x) Pn(x)为gate function的乘积。
在leaf node l l l有k个参数 θ a l ∈ R K θ_a^l ∈ R^K θal∈RK(通过梯度传播进行训练),k是类别,通过softmax函数得到一个概率分布,因此每个叶子结点都输出一个概率分布。文章选取有最大路径概率的叶子结点上的概率分布作为树的输出的概率分布(每个叶子结点都对应来一个路径概率)。

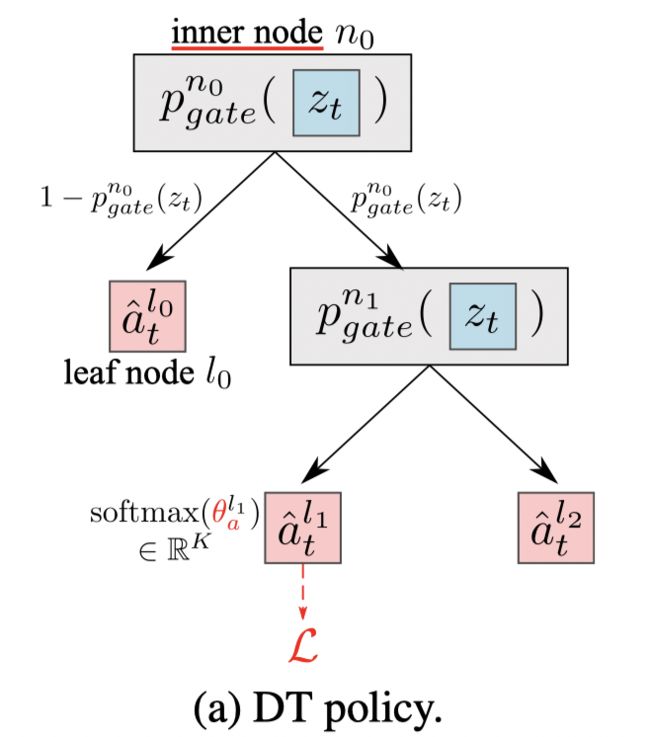
Recurrent Decision Tree
为了解释之前获取的信息,因为文章不止考虑当前观测值 z t z_t zt也考虑之前历史的表征 h t h_t ht。RDT将 h t h_t ht和 z t z_t zt作为输入,并且每个叶子结点多了两组参数, θ h l ∈ R M θ_h^l ∈ R^M θhl∈RM用于计算下一个time step的embedding, h t + 1 l = t a n h ( θ h l ) h^l_{t+1}= tanh(θ_h^l) ht+1l=tanh(θhl); θ z l ∈ R D θ_z^l∈ R^D θzl∈RD, 用于预测病人的下一步的观测值 z t + 1 z_{t+1} zt+1
Optimisation objective
SDT的损失函数:
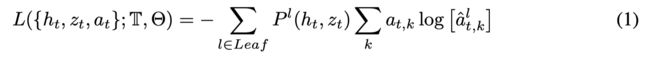
RDT损失函数:
最小化预测值的误差(第一项)并确保预测的观测值在策略下做出的动作与在真实观测值下的相似(第二项)
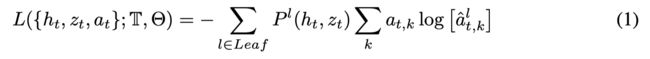
整体损失为SDF损失函数+RDT损失函数

Tree growth
从一个节点开始,不断地分裂内部节点为两个叶子结点并且优化参数,如果在验证集上的表现提升则接受该分裂。当不在分裂叶子结点以后,执行一个全局的参数优化,并且将在验证集上路径概率小于阈值的分支进行剪枝操作(有点像减少错误率剪枝,很依赖于验证集的数据分布。)
Evaluation
在医疗集上实验。下图为在ADNI dataset上的可视化。Magnetic Resonance Imaging (MRI)
Patient A is not ordered any further scan, as they never show low V hor abnormal CDR, but may be ordered one if they develop cognitive impairment.
Patient B with low V h but a CDR score not yet severe, another MRI is ordered to monitor disease progression.
Patient C’s observations already give a certain diagnosis of dementia: no scan is necessary.

Self-interpretable Modeling Method
这类方法关注于用一个具有自我可解释的模型来代替DRL中的深度神经网络,这样在训练后的模型不仅有好的Performance而已具有解释性。其中SDT和DDT都可以通过随机梯度下降算法训练。但这一类方法我认为并没有前景,最主要的原因就是这类机器学习模型表征能力不足。
*Distilling a Neural Network Into a Soft Decision Tree (2017,CEx@AIIA)
Intro
这篇文章首次提出的软决策树,一种可以利用梯度下降算法进行训练的决策树。文章用来对CNN的图像识别进行策略蒸馏,所以是一个模型逼近方法。算考虑到其可以进行梯度下降并且本身具有解释性,我认为这种方法也可以用来作为一个Self-interpretable Modeling的方法。但文章提出的决策树是一个提前设定深度的决策树,像神经网络结构一个是一个预先设置好的结构,没有提出拓展和剪枝的算法(POERREE会给出)。
**Designing Interpretable Approximations to Deep Reinforcement Learning with Soft Decision Trees (2020) **这篇文章将RL与软决策树相结合,但那篇文章我找不到pd并且只有background cite。
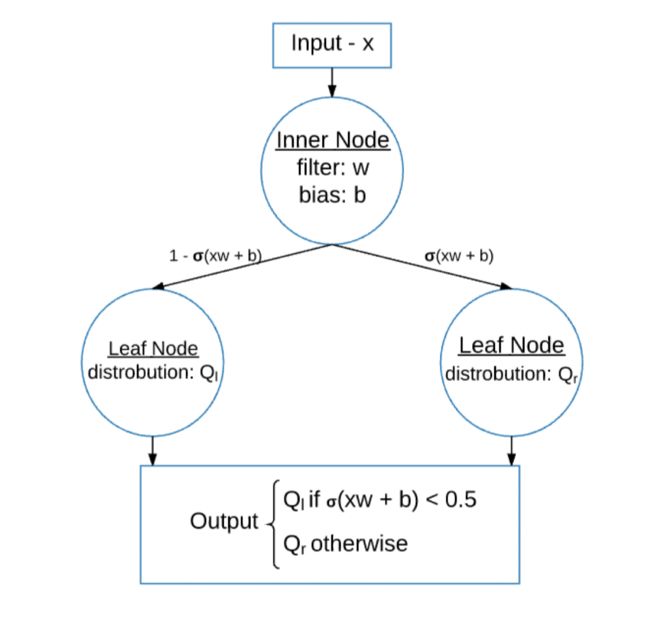
Model
在每一个内部结点(inner node) 选取右分支的概率为:

模型是一个hierarchical mixture of experts。这个模型学习到一个分层的过滤,通过一个路径概率将每个样本分配给一个bigot (也就是叶子结点),每一个bigot都学习一个在k个类别上的静态分布(所以文章提出的这个模型是用于做分类问题):

每个 φ l φ ^l φl都是可以通过梯度下降学习的参数。
为了避免 very soft decisions,文章引入了一个温度参数 β \beta β, 将选取右边支的概率变为 p i ( x ) = σ ( β ( x w i + b i ) ) p_i(x) = σ( β (xw_i+ b_i)) pi(x)=σ(β(xwi+bi))
文章给出了两种计算最后预测分布的方法。一种是选择有最大路径概率的叶子结点上的分布,一种是将每个叶子结点的路径概率✖️对应叶子结点上的概率分布后求和。
损失函数为计算每个叶子结点上概率分布和目标分布之间的交叉熵:
其中T是目标分布。
为了鼓励每个节点都平衡探索左右两个分支,则加入一个惩罚项,为一个节点选取左右分支的概率分布和均衡概率分布(0.5,0.5)之间的交叉熵。
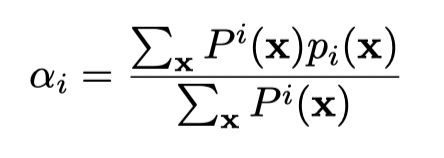

λ \lambda λ是一个超参数,随着深度d指数级衰减。
Evaluation
MNIST: 在这个数据集上设定深度为8,达到了94.45%的分类准确率,一个CNN可以到达99.21%的准确率,如果将真实概率分布替换为CNN输入的概率分布,则软决策树可以到达96.76%的分类准确率。我在实现中通过原始分布达到了 94%以上的准确率。
*Optimization Methods for Interpretable Differentiable Decision Trees in Reinforcement Learning(2019)
Intro
将随机梯度下降算法与传统决策树相结合,使得决策树可以通过梯度进行训练从而应用到Q-learning和policy gradient的方法上。并且树的结构不同于soft decision tree, 同时为了使得树有更好的解释性用过rule-list将树离散化表示。
Contributions
- we examine the properties of gradient descent over DDTs, motivating policygradient-based learning. To our knowledge, this is the first investigation of the optimization surfaces of Q-learning and policy gradients for DDTs
- Second, we compare our method with baseline approaches on standard RL challenges, showing that our approach parities or outperforms a neural network (但实际上表现得很差,所谓的baseline rl method本身就不是一个好的模型,所以和神经网络的比较我认为没有意义因为神经网络本身表现就很差)。 further, the interpretable decision trees we discretize after training achieve an average reward up to 7x higher than a batch-learned decision tree.
- Finally, we conduct a user study to compare the interpretability and usability of each method as a decision-making aid for humans, showing that discrete trees and decision lists are perceived as more helpful (p < 0.001) and are objectively more efficient (p < 0.001) than a neural network.
Model
Decision Tree

DDTs
在传统的决策树(例如CART)中,每个节点代表一个布尔决定(TRUE/FALSE). 在DDT中被替代为一个线性组合并且加上sigmoid函数(可以简单理解为树的节点变成了神经元的节点,但是保留了树的结构,因为树的结构是天然可以解释的,这点和soft decision tree思想一样)
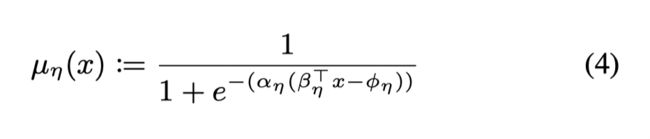
将DDT与RL结合,例如Q-learning,则每个叶子结点返回一个Q值,并通过随机梯度下降训练;策略梯度的方法则每个叶子结点代表在状态s下选取动作a的概率(应该要将动作离散化,并且每一个动作建一颗树)。一个节点求梯度的简单版本:
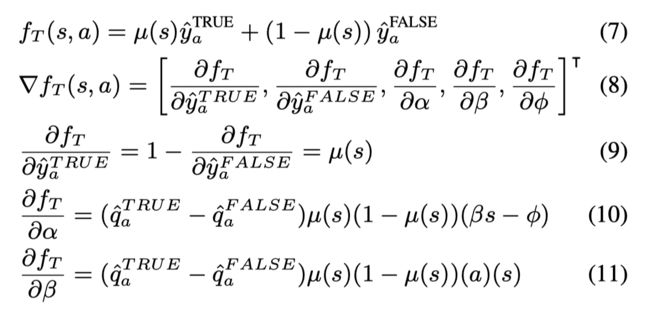
文章认为原版DDT存在两个问题,一个是线性组合而不是单个特征的比较(这点我不赞同,线性组合的权重可以用来表示在这个状态决策下每个观测特征的重要性),二是激活函数的存在使得在分支选择上有一个smooth transition 而不是一个离散的决策(就是简单用一个值来比较,像传统决策树一样)。因此文章采用了一个 rule list architecture。
为了将树的决策变为完全离散的, β n \beta_n βn采用one-hot编码。同时将 ϕ n \phi_n ϕn除以 β n j \beta_n^j βnj,这样每一个节点都会是某一个原始的输入特征和一个单一的 ϕ n \phi_n ϕn比较,就把公式3转化为了公式4。同样在叶子结点必须返回一个动作,因此也将叶子结点设为one-hot编码。
the rule- or decision-list:
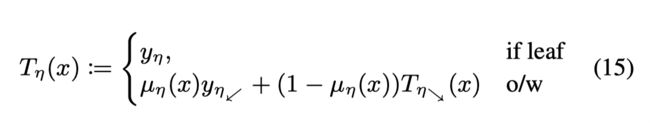
最终树的展示:

关于这块我的理解是在树训练好后,权重都已经形成后,为了使树更具解释性从而将树离散化。否则有两个问题:1.把公式4专为公式3以后,那树就和传统的决策树一样了,并不是像DDT可以利用梯度训练。2.把树改成这种结构以后,文章也没有提到具体的训练框架以及这种结构为什么还是Differentiable。后面实验也说明了应该是这样。
Evaluation
从实验结果来看,首先MLP(PPO)在lunarlander中只有87本身就说明这是一个不太好的策略,并且无论哪种模型都没有200的收益就说明都没学出策略,因此有关MLP的对比都没有什么意义。虽然DDT没能在lunar lander中学出最优的策略,但学出了一个不会坠毁的飞行策略。并且离散化后的表现明显下降。值得一提的是state- action DT也不可能只有这种表现,除非采集的样本数非常少,否则从一个训练好的RL中采集个10000的样本数就能达到500的收益了。
Conservative Q-Improvement: Reinforcement Learning for an Interpretable Decision-Tree Policy (2019)
Intro
文章是一种decision-tree-via-RL approach的方法。CAI学习一颗决策树,通过判断是否会提升决策树的表现来增加结点。
Contributions
Conservative Q-Improvement (CQI) reinforcement learning algorithm. CQI learns a policy in the form of a decision tree, is applicable to any domain in which the state space can be represented as a vector of features, and generates a human-interpretable decision tree policy.
Model
只有当新策略的期望收益增加超过一个阈值才会进一步分裂,这个阈值随着训练逐渐减少,并且在一次分裂后设为初始值。也是因为这个文章认为方法是Conservative。

选取动作的策略,也是 ϵ − g r e e e d y \epsilon-greeedy ϵ−greeedy的

叶子结点的Q值通过标准的贝尔曼最优方程来更新。每个叶子结点包括:一组Q值(一个动作一个Q),访问频率和所有可能的 split。下面为Q值更新和访问频率更新:
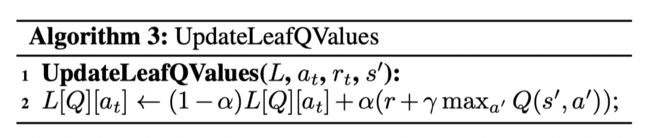

其中sibling 代表N的孩子结点。
每个叶子结点都会不断记录并更新所有可能的splits, L [ Q ] [ a ] L[Q][a] L[Q][a] refers to the Q Q Q value of action a a a on node L L L.

通过最大的 ∆ Q ∆Q ∆Q 来选择最佳split。如果最大的 ∆ Q ∆Q ∆Q大于设定阈值,则进行对应分裂,否则,阈值衰减。

分裂结点:

Evaluation
文章在RobotNav上进行实验。


Post-hoc Interpretation Method
这种方法区别于以上尝试解释模型,或者说模型中的黑盒模型中代表的映射函数,尝试从其他角度给出策略的解释性。其中基于因果模型的文章尝试给出做出某个动作,或者不做出某个动作的解释,其解释性会更好但不具备决策的能力,关于这方面的文章可以参考泽武的总结,我并不了解。APG通过图模型来给出策略和环境的状态转移概率。EDGE则分析在一个episode中重要的time steps.
*Programmatically Interpretable Reinforcement Learning (2018, ICML)
PIRL represents policies using a high-level, domain-specific programming language。We propose a new method, called Neurally Directed Program Search (NDPS), for solving the challenging nonsmooth optimization problem of finding a programmatic policy with maximal reward. NDPS works by first learning a neural policy network using DRL, and then performing a local search over programmatic policies that seeks to minimize a distance from this neural “oracle”.
*Explainable Reinforcement Learning Through a Causal Lens (2019, AAAI)
Intro
基于因果关系提出了一个 action influence模型,关注于 “why” and "why not"问题,也就是为什么做了某个动作以及为什么不做某个动作,从而给出解释性。假设每一个变量之间都有因果关系,那同时也可以学习到每个动作对变量的影响。这篇文章提出的因果模型应该是从社会心理学发展而来。
Contributions
- We introduce and formalise the action influence model based on structural causal models and present definitions to generate explanations
- We conduct a between-subject human study to evaluate the proposed model with baselines.
Evaluation

Example

*Generation of Policy-Level Explanations for Reinforcement Learning (2019, AAAI)
Intro
文章提出了Abstract Policy Graphs (APGs)作为策略的一个抽象。每一个APG都是一张图,每个图的结点都是一个抽象状态并且每一个边都是一个动作并有一个状态转移概率。通过这个图,我们可以知道agent将哪些状态视为相似的,并且可以预测接下去会采取的动作。文章提出APG Gen算法,根据特征重要性不断进行抽象状态空间的划分,因此通过这个划分过程也可以给出对每个抽象状态,特征的重要性。
Contributions
- we introduce a novel representation, Abstract Policy Graphs, for summarizing policies to enable explanations of individual decisions in the context of future transitions
- we propose a process, APG Gen, for creating an APG from a policy and learned value function,
- we prove that APG Gen’s runtime is favorable $ (O( | F |^2 | tr_ samples | )$, where F F F is the set of features and t r _ s a m p l e s tr \_samples tr_samples is the set of provided transitions)
- we empirically evaluate APG Gen’s capability to create the desired explanations.
Model
Feature Importance Function
一个重要性函数 I f ( c ) I_f(c) If(c)代表了特征 f f f的重要性,文章采用Feature Importance Ranking Measure (FIRM),对于二元特征计算快速并且易于解释。
FIRM使用了一个conditional expected score:
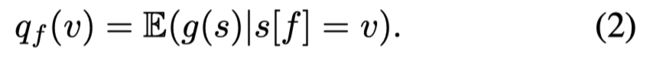
对于特征 f f f 取 v v v 的状态 s s s 的一个平均得分。如果 q f ( v ) q_f(v) qf(v) 是一个平的函数,则说明该特征重要性不高。如果 q f ( v ) q_f(v) qf(v) 的变化剧烈,则说明该特征的重要性较高。因此FIRM定义一个特征的重要性为:
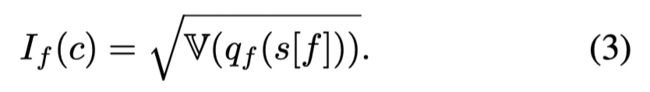
文章将特征 f f f取为二元特征, 这样上式就变为:
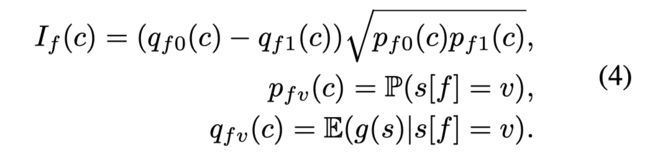
Abstract Policy Graphs
定义一个映射函数 l ( s ) l(s) l(s),将MDP中的状态(grounded state)映射到抽象的状态。抽象状态集合中的每个状态在agent策略下都是interchangeable,也就是在某些agent做出相似行动的状态(一个抽象状态)中,会让agent专向的状态也是具有相似动作的(另一个抽象状态)。例如:

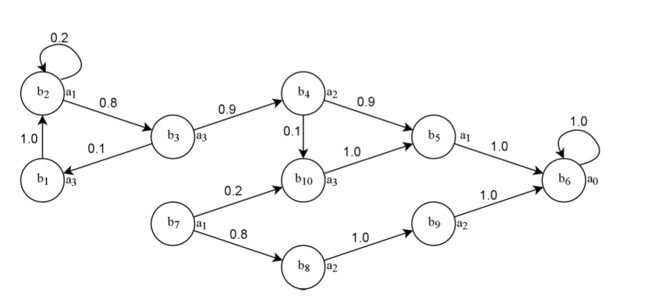
考虑到关于抽象状态之间的转移概率的计算是通过 grounded state 的平均转移概率进行逼近,因此对于随机环境就算导致这种估计不准。因此文章做了一个简单的马尔可夫假设:the abstract state reached, b t + 1 b_{t+1} bt+1 , when performing an action depends only on the current abstract state, b t b_t bt.
APG Construction
文章利用 V π ( s ) V_{\pi}(s) Vπ(s)作为得分函数。
Splitting Binary Features
在文章中所有的特征的都是二元的,因此如果一个数据集根据 f f f进行分裂,因此所有的子集都应该有 I f = 0 I_f=0 If=0。因此这个分裂过程可以不断运用直到所有的特征的重要性都变低。这些二元特征需要进行预处理,但计算V值用原来的特征,因为V值的计算只和状态有关,和特征的选取无关。
Abstract State Division
不断分割有最大 I f I_f If 的数据集。

APG Edge Creation
转移概率为在一个抽象状态中的,转移到其他抽象状态的样本的比例。

TripleTree: A Versatile Interpretable Representation of Black Box Agents and their Environments(2020,AAAI)
Intro
基于state abstract到概念,文章提出了一种树用于进行状态空间的划分并且估计状态转移概率。而划分的准则不同于传统的决策树,结合了在状态空间的动作是否相同,在状态空间的表现(状态值估计)是否相同,定义相似度通过temporal dynamics 这三种划分标准。文章假设黑盒和环境都是内在不可知的,我们的模型只是一个观察者,可以记录状态,动作和收益。
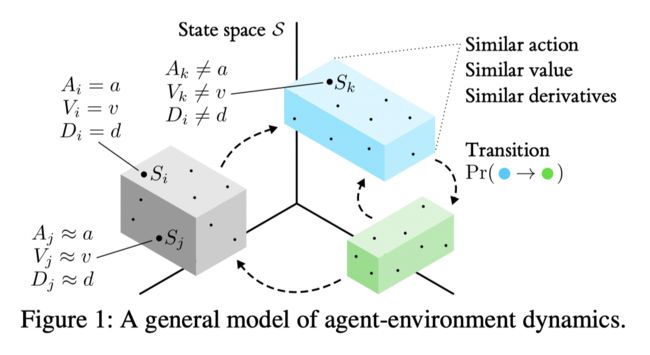
Key Features
- Acceptance of the triplet observations in D, calculation of value and state derivatives for each sample, and storage of predicted values of these variables at each leaf.
- A hybrid measure of partition quality Q ∗ , mediated by a weight vector θ, which trades off the tree’s abilities to predict the target agent’s action, value and state derivatives.
- Calculation of P L P_L PL and $ T_L$ to encode information about temporal dynamics in terms of leaf-to-leaf transitions.
- A best-first growth strategy.
Model
基于传统解决树的分裂结点想法,都是基于最大化某一个量(结点纯度)的减少,只不过这个量(纯度)的计算公式不同。
每个叶子结点都有三个预测值: the action a ~ L \tilde a_L a~L , a value estimate v ~ L \tilde v_L v~L (the mean of the leaf’s contituent samples), and a state derivative estimate d ~ L \tilde d_L d~L (the elementwise mean).
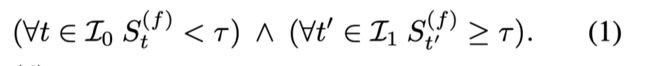

Action quality Q ( A ) Q^{(A)} Q(A):
对于离散的动作空间空间使用基尼指数:
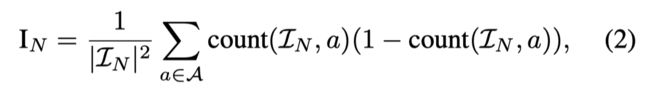
对于连续的动作空间使用方差:
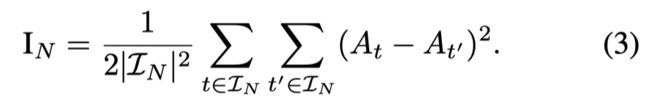
Value quality Q ( V ) Q^{(V)} Q(V): 纯度函数使用状态值函数 V t V_t Vt估计的方差。
Derivative quality Q ( D ) Q^{(D)} Q(D): 纯度函数sums the variance in derivatives across all d of the feature dimensions:

在得到了三个量后,文章将他们做一个线性组合:

其中 θ \theta θ 是一个权重向量,是一个预先设置好的值,在训练过程中不进行调整。
传统CART遵循一个 depth- first的原则,也就是每个结点都对所有叶子结点进行分裂快速增长树的深度。而文章遵循了一个 best-first的策略,也就是在每个分裂阶段,只一个表现最好的叶子结点进行分裂:

同时也通过限制叶子结点的样本数来判断是否继续分裂。
计算叶子结点的之间的转移概率
让 l e a f ( t ) = L : t ∈ I L leaf(t) = L :t \in I_L leaf(t)=L:t∈IL 表示t时刻的样本属于叶子结点$
定义一个 I L I_L IL的一个子集,也就是t时刻在叶子结点L而t-1时刻不在。对于一个序列初始的样本 t ∈ I L ∗ t \in I_L^* t∈IL∗, 有如下定义:

从一个开始结点 L L L到一个目标结点 L ′ L' L′,定义 I L ∗ I^*_L IL∗中的一个子集为:
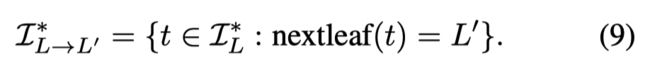
则由 L L L 到 L ′ L' L′转移概率和转移次数由如下定义:
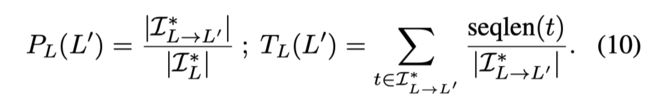
P P P和 L L L分别代表任意一段在 L L L中的序列最终会在某一时刻跳转至 L ′ L' L′的概率以及序列的平均长度。
Evaluation
在一个简单的交通环境中进行实验。
Feature-Based Interpretable Reinforcement Learning based on State-Transition Models (2021,IEEE)
Intro
文章通过一个agent和环境交互得到的数据进行分析。文章采用risk而不是reward。
Method Propertity
- Offer local explanations
- Offer explanations in terms of the importance of actionable features
- Offer explanations about the risks the model will be facing
- Be a post-hoc approach applicable to any arbitrary RL algorithm
- Require minimal changes to the learning pipeline
- Be applicable to environments with either continuous or discrete state and action spaces
Model
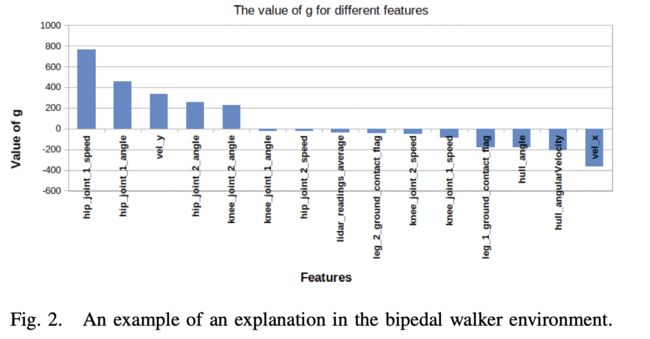
首先策略的目标是寻找risk的方向(定义为g,一个状态空间中的向量),使得以g的方向改变状态会增加agent的目标函数值。
定义 state-risk function 为 R s : ( S → [ 0 , 1 ] ) R ^s:(S → [0, 1]) Rs:(S→[0,1]) 来确定一个状态是否是risky的。这个函数可以由人类专家定义。
定义一个特征为 Actionable Features 如果在这个特征的值增加,风险也会增加。
为了给出当前状态 s s s 的解释性,文章利用状态转移模型(后面学习的)生成一个集合 S ∗ S^* S∗, 可以通过至多n个动作由agent接触到状态集合。目标函数定义每一个元素的risk, 利用 R ∗ R^* R∗ 进行估计。用于一个线性模型来估计risk,如果risk是二元的,则可以用线性分类器;如果是连续值,则可以用线性回归。线性模型的权重可以被认为是risk的一个搜索方向。
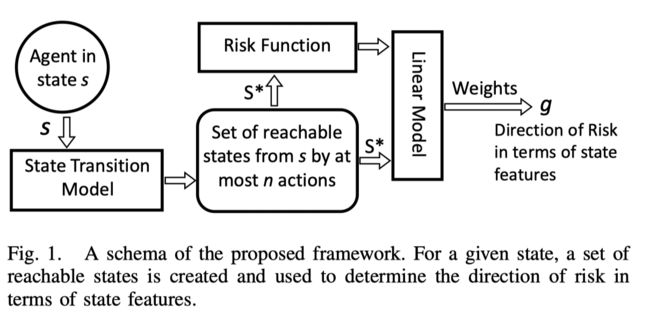
鉴于上述概念过于抽象,文章提出了一个具体的实现方式
Concrete Solution
Fatal state定义为一个episode因为某些错误而结束的状态。
Supercritical states 定义为没有一种已知的策略,能避免这些状态变成fatal状态。
文章将上述两种状态定义为risky。
接下来状态转移模型其实和APG一样,就是一张图。只不过每个点中的状态有个特点:离该结点的代表状态的距离比离其他结点的代表状态的距离小。这个思想和K聚类比较相似。并且边上面没有动作信息,只代表至少有一个动作存在。
文章降构建图的过程与DRL与环境交互同时进行。每次交互得到一组数据,把这组数据加入图中。
对于离散的状态空间,每一个节点都可以是一个单独的动作。如果一个新的状态发现不在图中,则加入图中。并且如果一个新的转移发现不在图中,则给图中对应节点加上一条边。
对于连续的状态空间,文章定义一个 ϵ \epsilon ϵ 的半径。如果一个新状态,不在任何一个节点的代表状态的半径中,则创建一个新的结点,该状态为这个结点的代表状态。边的创建同离散动作一样。
任意一个节点中如果有一个fatal状态就定义为risky,任意节点的出边连接到一个risky节点,则该结点也定义为risky。如果一个节点的risky的,则该结点中所有状态都是risky的。
为了提供解释性,首先找到一个状态 s s s的代表结点 n τ n_{\tau} nτ,并基于广度优先搜索,设置搜索深度为n,遍历得到的所有状态作为 S ∗ S^* S∗ 的近似。则线性模型在 S ∗ S^* S∗ 上训练并注意 S ∗ S^* S∗里包括的是结点中的代表状态而不是所有状态。
Evaluation
文章在Bidepalwalker 和 lunarlander 上进行实验。
*EDGE: Explaining Deep Reinforcement Learning Policies (2021, NeuralPS)
Intro
传统的可解释方法关注于观测值和动作之间的关系,这篇文章是关注于策略层面的解释,他们将episode作为模型输入,通过RNN提取出每个time step下state-action的embeeding和每个episode的embedding, 将这些embeding 输入一个高斯过程,并且将高斯过程的输出输入一个基于线性回归的预测模型,将final reward作为模型输出。通过这个并且识别在一个episode中,有哪些重要的time step对最终的收益较大,和每个time step之间的关系以及不同episode之间的相似度,这样可以通过这些time step对策略进行解释,并且还可以进行对手的决策干扰和我方的漏洞修补。
Contributions
- we augment a Gaussian Process (GP) with a customized deep additive kernel to capture not only correlations between time steps but, more importantly, the joint effect across episodes.
- we combine this deep GP model with our newly designed explainable prediction model to predict the final reward and extract the time step importance.
- we develop an efficient inference and learning framework for our model by leveraging inducing points and variational inference.
文章考虑了另外两种具有自我解释性并且可以用来处理序列数据的模型,RNN augmented with attention and rationale net 尽管都具有可解释性,但这种方法无法有效捕捉到episode之内 time step的联系和episode之间的联系。文章提出的模型结构和这两个模型相似,都有一个特征提取器(例如RNN的权重和attention层),输出可以用于识别在输入序列中重要的step和一个预测模型。
Model
模型分为三个部分
-
RNN encoder: 这个一个embedding层,用来获得latent representation of episode。其中 X ( i ) = { s t ( i ) , a t ( i ) } t = 1 : T X^{(i)}= \{s_t^{(i)}, a_t^{(i)}\}_{t=1:T} X(i)={st(i),at(i)}t=1:T,作为一个episode的信息,通过RNN提取出 h T i h_T^i hTi作为state-action embedding。同时也将最有一个step的embedding输入一个MLP层提出episode的embeeding e ( i ) e^{(i)} e(i)。SE kernel 的输入空间为欧式空间,对高纬数据来说难以处理,所以这个RNN层可以认为是一个降维层。
-
Additive GP with Deep Recurrent Kernels:作为特征提取器,用来获得latent representation of the whole episode f 1 : T ( i ) f_{1:T}^{(i)} f1:T(i),并且用来捕捉不同time steps和episode之间的关系。高斯过程是一个统计模型,假设每一个样本都服从一个高斯分布,每个样本对应一个非参函数有一个高斯先验,服从于一个正态分布,并且多个函数服从于多元正态分布, f ∼ G P ( 0 , k γ ) f ∼ G P(0, k_γ) f∼GP(0,kγ), ( f ∣ X ) ∼ N ( 0 , K X X ) (f | X) ∼ N(0, K_{XX}) (f∣X)∼N(0,KXX), $(K_{XX}){ij} = k\gamma(x_i,x_j) $其中kernel function 为square exponential (SE) kernel function:
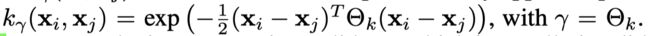
这个GP模型包含了两个部分, f t f_t ft和 f e f_e fe。其中 f t ∼ G P ( 0 , k γ t ) f_t∼ G P(0, k_{γt}) ft∼GP(0,kγt)捕捉了不同time step之间的关系, f e ∼ G P ( 0 , k γ e ) f_e∼ G P(0, k_{γe)} fe∼GP(0,kγe)捕捉了不同episode之间的相似度。最后additive GP model可以表示为:
-
prediction model:将一个线性回归模型作为预测模型的基础,线性回归的权重可以反应输入的重要性(也就是time step的重要性)。当 y i y_i yi是连续的时候,使用传统的高斯回归模型, y i = F ( i ) w T + ϵ 1 y_i= F^{(i)}w^T + \epsilon_1 yi=F(i)wT+ϵ1,则条件似然分布为: y i ∣ F ( i ) ∼ N ( F ( i ) w T , σ 2 ) y_i| F^{(i)}∼ N(F^{(i)}w^T, σ^2) yi∣F(i)∼N(F(i)wT,σ2)。对于离散的reward,采用softmax.
Posterior Inference and Parameter Learning
-
Sparse GP with Inducing Points:按照传统方式去计算高斯过程只适用于小规模的数据集,因为文章提出了inducing points method,用于将有效的样本数量从 N T NT NT降到 M M M(文章没有介绍这个方法),将inducing point 定义为 z i ∈ R 2 q z_i∈ R^{2q} zi∈R2q, u i u_i ui 为GP output, f 和 u 的联合先验证以及条件先验证 f ∣ u f|u f∣u 为:
-
**Variational Inference and Learning:**利用经验贝叶斯最大化log marginal likelihood,为了简化计算,文章假设inducing point服从一个variational posterior 和一个可分解的联合后验 q ( f , u ) = q ( u ) p ( f ∣ u ) q(f, u) = q(u)p(f | u) q(f,u)=q(u)p(f∣u), 通过Jensen’s inequality,我们可以得到evidence lower bound (ELBO):

第一项是概率似然,第二项是先验证和后验证。对于分类可以采用重参数技巧。
Evaluation
- pong game: EDGE highlights the time steps when the agent hits the ball as the key steps leading to a win, the last few steps that the target agent misses the ball as the critical step in the losing episode.
- You-Shall-Not Pass: in the left episode of Fig. 3(b), our explanations state that the runner (red agent) wins because it escapes from the blocker and crosses the finish line.
在最长的一段连续重要的time step上改变策略来进行实验。(例如红色部分)
- Attacks: If an agent’s win mainly relies on its actions at a few crucial steps, then the agent could easily lose if it takes sub-optimal actions at those steps. 在赢的场次中,对关键的步骤增加扰动。
- **patching:**The key idea is to explore a remediation policy by conducting explorations at the critical time steps of losing games and use the mixture of the original policy and the remediation policy as the patched policy. 在输的场次中,对关键步骤采取其他策略。
- Roubusifying: we propose to robustify the victim agent by blinding its observation on the adversary at the critical time steps in the losing episode。发现在游戏中,对手输掉可能是被我方的动作干扰的了,因此在对手输掉的关键步骤上使对手不观测到我们的行为。