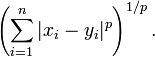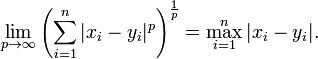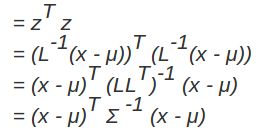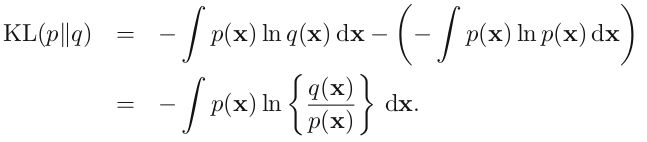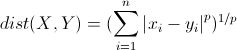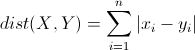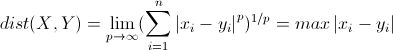机器学习中距离和相似性度量方法
机器学习中距离和相似性度量方法
在机器学习和数据挖掘中，我们经常需要知道个体间差异的大小，进而评价个体的相似性和类别。最常见的是数据分析中的相关分析，数据挖掘中的分类和聚类算法，如 K 最近邻（KNN）和 K 均值（K-Means）等等。根据数据特性的不同，可以采用不同的度量方法。一般而言，定义一个距离函数 d(x,y), 需要满足下面几个准则：
1) d(x,x) = 0 // 到自己的距离为0
2) d(x,y) >= 0 // 距离非负
3) d(x,y) = d(y,x) // 对称性: 如果 A 到 B 距离是 a，那么 B 到 A 的距离也应该是 a
4) d(x,k)+ d(k,y) >= d(x,y) // 三角形法则: (两边之和大于第三边)
这篇博客主要介绍机器学习和数据挖掘中一些常见的距离公式，包括：
- 闵可夫斯基距离
- 欧几里得距离
- 曼哈顿距离
- 切比雪夫距离
- 马氏距离
- 余弦相似度
- 皮尔逊相关系数
- 汉明距离
- 杰卡德相似系数
- 编辑距离
- DTW 距离
- KL 散度
1. 闵可夫斯基距离
闵可夫斯基距离（Minkowski distance）是衡量数值点之间距离的一种非常常见的方法，假设数值点 P 和 Q 坐标如下：
那么，闵可夫斯基距离定义为：
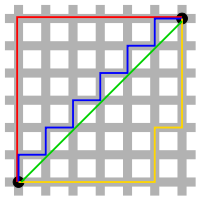
该距离最常用的 p 是 2 和 1, 前者是欧几里得距离（Euclidean distance），后者是曼哈顿距离（Manhattan distance）。假设在曼哈顿街区乘坐出租车从 P 点到 Q 点，白色表示高楼大厦，灰色表示街道：
绿色的斜线表示欧几里得距离，在现实中是不可能的。其他三条折线表示了曼哈顿距离，这三条折线的长度是相等的。
当 p 趋近于无穷大时，闵可夫斯基距离转化成切比雪夫距离（Chebyshev distance）：
我们知道平面上到原点欧几里得距离（p = 2）为 1 的点所组成的形状是一个圆，当 p 取其他数值的时候呢？
注意，当 p < 1 时，闵可夫斯基距离不再符合三角形法则，举个例子：当 p < 1, (0,0) 到 (1,1) 的距离等于 (1+1)^{1/p} > 2, 而 (0,1) 到这两个点的距离都是 1。
闵可夫斯基距离比较直观，但是它与数据的分布无关，具有一定的局限性，如果 x 方向的幅值远远大于 y 方向的值，这个距离公式就会过度放大 x 维度的作用。所以，在计算距离之前，我们可能还需要对数据进行 z-transform 处理，即减去均值，除以标准差：
: 该维度上的均值
: 该维度上的标准差
可以看到，上述处理开始体现数据的统计特性了。这种方法在假设数据各个维度不相关的情况下利用数据分布的特性计算出不同的距离。如果维度相互之间数据相关（例如：身高较高的信息很有可能会带来体重较重的信息，因为两者是有关联的），这时候就要用到马氏距离（Mahalanobis distance）了。
2. 马氏距离
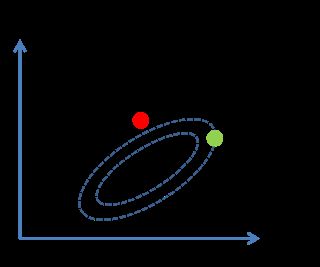
考虑下面这张图，椭圆表示等高线，从欧几里得的距离来算，绿黑距离大于红黑距离，但是从马氏距离，结果恰好相反：
马氏距离实际上是利用 Cholesky transformation 来消除不同维度之间的相关性和尺度不同的性质。假设样本点（列向量）之间的协方差对称矩阵是 
， 通过 Cholesky Decomposition（实际上是对称矩阵 LU 分解的一种特殊形式，可参考之前的博客）可以转化为下三角矩阵和上三角矩阵的乘积： 
。消除不同维度之间的相关性和尺度不同，只需要对样本点 x 做如下处理：
。处理之后的欧几里得距离就是原样本的马氏距离：为了书写方便，这里求马氏距离的平方）：
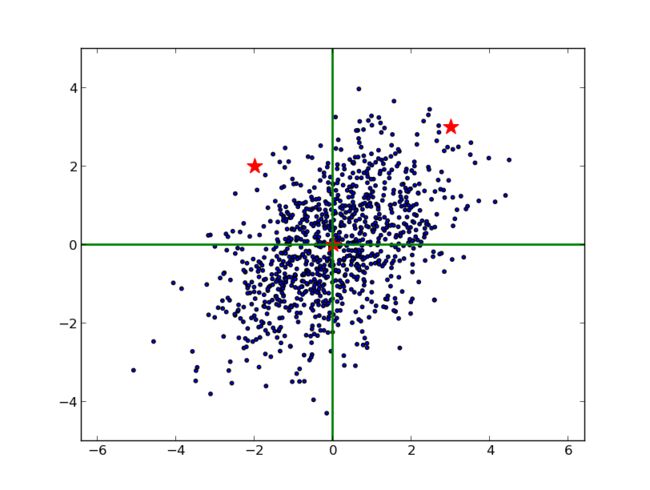
下图蓝色表示原样本点的分布，两颗红星坐标分别是（3, 3），（2, -2）:
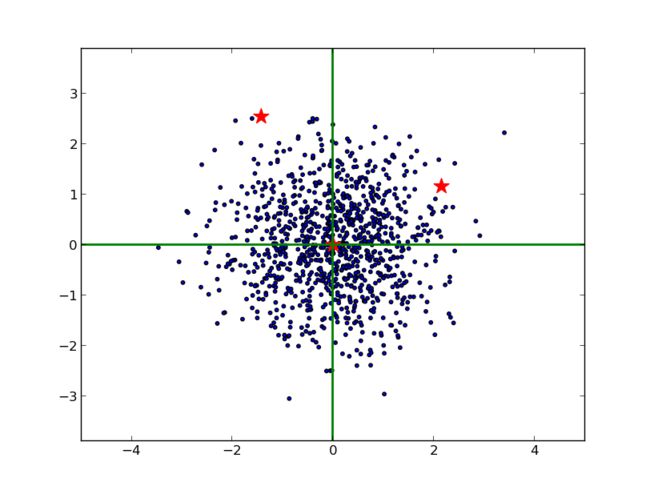
由于 x， y 方向的尺度不同，不能单纯用欧几里得的方法测量它们到原点的距离。并且，由于 x 和 y 是相关的（大致可以看出斜向右上），也不能简单地在 x 和 y 方向上分别减去均值，除以标准差。最恰当的方法是对原始数据进行 Cholesky 变换，即求马氏距离（可以看到，右边的红星离原点较近）：
将上面两个图的绘制代码和求马氏距离的代码贴在这里，以备以后查阅：
# -*- coding=utf-8 -*-
# code related at: http://www.cnblogs.com/daniel-D/
import numpy as np
import pylab as pl
import scipy.spatial.distance as dist
def plotSamples(x, y, z=None):
stars = np.matrix([[3., -2., 0.], [3., 2., 0.]])
if z is not None:
x, y = z * np.matrix([x, y])
stars = z * stars
pl.scatter(x, y, s=10) # 画 gaussian 随机点
pl.scatter(np.array(stars[0]), np.array(stars[1]), s=200, marker='*', color='r') # 画三个指定点
pl.axhline(linewidth=2, color='g') # 画 x 轴
pl.axvline(linewidth=2, color='g') # 画 y 轴
pl.axis('equal')
pl.axis([-5, 5, -5, 5])
pl.show()
# 产生高斯分布的随机点
mean = [0, 0] # 平均值
cov = [[2, 1], [1, 2]] # 协方差
x, y = np.random.multivariate_normal(mean, cov, 1000).T
plotSamples(x, y)
covMat = np.matrix(np.cov(x, y)) # 求 x 与 y 的协方差矩阵
Z = np.linalg.cholesky(covMat).I # 仿射矩阵
plotSamples(x, y, Z)
# 求马氏距离
print '\n到原点的马氏距离分别是：'
print dist.mahalanobis([0,0], [3,3], covMat.I), dist.mahalanobis([0,0], [-2,2], covMat.I)
# 求变换后的欧几里得距离
dots = (Z * np.matrix([[3, -2, 0], [3, 2, 0]])).T
print '\n变换后到原点的欧几里得距离分别是：'
print dist.minkowski([0, 0], np.array(dots[0]), 2), dist.minkowski([0, 0], np.array(dots[1]), 2)
马氏距离的变换和 PCA 分解的白化处理颇有异曲同工之妙，不同之处在于：就二维来看，PCA 是将数据主成分旋转到 x 轴（正交矩阵的酉变换），再在尺度上缩放（对角矩阵），实现尺度相同。而马氏距离的 L逆矩阵是一个下三角，总体来说是一个仿射变换。
3. 向量内积
向量内积是线性代数里最为常见的计算，实际上它还是一种有效并且直观的相似性测量手段。向量内积的定义如下：
直观的解释是：如果 x 高的地方 y 也比较高， x 低的地方 y 也比较低，那么整体的内积是偏大的，也就是说 x 和 y 是相似的。举个例子，在一段长的序列信号 A 中寻找哪一段与短序列信号 a 最匹配，只需要将 a 从 A 信号开头逐个向后平移，每次平移做一次内积，内积最大的相似度最大。信号处理中 DFT 和 DCT 也是基于这种内积运算计算出不同频域内的信号组分（DFT 和 DCT 是正交标准基，也可以看做投影）。向量和信号都是离散值，如果是连续的函数值，比如求区间[-1, 1] 两个函数之间的相似度，同样也可以得到（系数）组分，这种方法可以应用于多项式逼近连续函数，也可以用到连续函数逼近离散样本点（最小二乘问题，OLS coefficients）中，扯得有点远了- -!。
向量内积的结果是没有界限的，一种解决办法是除以长度之后再求内积，这就是应用十分广泛的余弦相似度（Cosine similarity）：
余弦相似度与向量的幅值无关，只与向量的方向相关，在文档相似度（TF-IDF）和图片相似性（histogram）计算上都有它的身影。需要注意一点的是，余弦相似度受到向量的平移影响，上式如果将 x 平移到 x+1, 余弦值就会改变。怎样才能实现平移不变性？这就是下面要说的皮尔逊相关系数（Pearson correlation），有时候也直接叫相关系数:
皮尔逊相关系数具有平移不变性和尺度不变性，计算出了两个向量（维度）的相关性。不过，一般我们在谈论相关系数的时候，将 x 与 y 对应位置的两个数值看作一个样本点，皮尔逊系数用来表示这些样本点分布的相关性。
由于皮尔逊系数具有的良好性质，在各个领域都应用广泛，例如，在推荐系统根据为某一用户查找喜好相似的用户,进而提供推荐，优点是可以不受每个用户评分标准不同和观看影片数量不一样的影响。
4. 分类数据点间的距离
汉明距离（Hamming distance）是指，两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。举个维基百科上的例子：
还可以用简单的匹配系数来表示两点之间的相似度——匹配字符数/总字符数。
在一些情况下，某些特定的值相等并不能代表什么。举个例子，用 1 表示用户看过该电影，用 0 表示用户没有看过，那么用户看电影的的信息就可用 0,1 表示成一个序列。考虑到电影基数非常庞大，用户看过的电影只占其中非常小的一部分，如果两个用户都没有看过某一部电影（两个都是 0），并不能说明两者相似。反而言之，如果两个用户都看过某一部电影（序列中都是 1），则说明用户有很大的相似度。在这个例子中，序列中等于 1 所占的权重应该远远大于 0 的权重，这就引出下面要说的杰卡德相似系数（Jaccard similarity）。
在上面的例子中，用 M11 表示两个用户都看过的电影数目，M10 表示用户 A 看过，用户 B 没看过的电影数目，M01 表示用户 A 没看过，用户 B 看过的电影数目，M00 表示两个用户都没有看过的电影数目。Jaccard 相似性系数可以表示为：
Jaccard similarity 还可以用集合的公式来表达，这里就不多说了。
如果分类数值点是用树形结构来表示的，它们的相似性可以用相同路径的长度来表示，比如，“/product/spot/ballgame/basketball” 离“product/spot/ballgame/soccer/shoes” 的距离小于到 "/product/luxury/handbags" 的距离，以为前者相同父节点路径更长。
5. 序列之间的距离
上一小节我们知道，汉明距离可以度量两个长度相同的字符串之间的相似度，如果要比较两个不同长度的字符串，不仅要进行替换，而且要进行插入与删除的运算，在这种场合下，通常使用更加复杂的编辑距离（Edit distance, Levenshtein distance）等算法。编辑距离是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。编辑距离求的是最少编辑次数，这是一个动态规划的问题，有兴趣的同学可以自己研究研究。
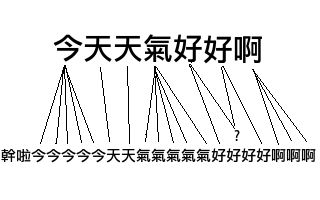
时间序列是序列之间距离的另外一个例子。DTW 距离（Dynamic Time Warp）是序列信号在时间或者速度上不匹配的时候一种衡量相似度的方法。神马意思？举个例子，两份原本一样声音样本A、B都说了“你好”，A在时间上发生了扭曲，“你”这个音延长了几秒。最后A:“你~~~好”，B：“你好”。DTW正是这样一种可以用来匹配A、B之间的最短距离的算法。
DTW 距离在保持信号先后顺序的限制下对时间信号进行“膨胀”或者“收缩”，找到最优的匹配，与编辑距离相似，这其实也是一个动态规划的问题:
实现代码（转自 McKelvin's Blog ）:
#!/usr/bin/python2
# -*- coding:UTF-8 -*-
# code related at: http://blog.mckelv.in/articles/1453.html
import sys
distance = lambda a,b : 0 if a==b else 1
def dtw(sa,sb):
'''
>>>dtw(u"干啦今今今今今天天气气气气气好好好好啊啊啊", u"今天天气好好啊")
2
'''
MAX_COST = 1<<32
#初始化一个len(sb) 行(i)，len(sa)列(j)的二维矩阵
len_sa = len(sa)
len_sb = len(sb)
# BUG:这样是错误的(浅拷贝): dtw_array = [[MAX_COST]*len(sa)]*len(sb)
dtw_array = [[MAX_COST for i in range(len_sa)] for j in range(len_sb)]
dtw_array[0][0] = distance(sa[0],sb[0])
for i in xrange(0, len_sb):
for j in xrange(0, len_sa):
if i+j==0:
continue
nb = []
if i > 0: nb.append(dtw_array[i-1][j])
if j > 0: nb.append(dtw_array[i][j-1])
if i > 0 and j > 0: nb.append(dtw_array[i-1][j-1])
min_route = min(nb)
cost = distance(sa[j],sb[i])
dtw_array[i][j] = cost + min_route
return dtw_array[len_sb-1][len_sa-1]
def main(argv):
s1 = u'干啦今今今今今天天气气气气气好好好好啊啊啊'
s2 = u'今天天气好好啊'
d = dtw(s1, s2)
print d
return 0
if __name__ == '__main__':
sys.exit(main(sys.argv))
6. 概率分布之间的距离
前面我们谈论的都是两个数值点之间的距离，实际上两个概率分布之间的距离是可以测量的。在统计学里面经常需要测量两组样本分布之间的距离，进而判断出它们是否出自同一个 population，常见的方法有卡方检验（Chi-Square）和 KL 散度（ KL-Divergence），下面说一说 KL 散度吧。
先从信息熵说起，假设一篇文章的标题叫做“黑洞到底吃什么”，包含词语分别是 {黑洞, 到底, 吃什么}, 我们现在要根据一个词语推测这篇文章的类别。哪个词语给予我们的信息最多？很容易就知道是“黑洞”，因为“黑洞”这个词语在所有的文档中出现的概率太低啦，一旦出现，就表明这篇文章很可能是在讲科普知识。而其他两个词语“到底”和“吃什么”出现的概率很高，给予我们的信息反而越少。如何用一个函数 h(x) 表示词语给予的信息量呢？第一，肯定是与 p(x) 相关，并且是负相关。第二，假设 x 和 y 是独立的（黑洞和宇宙不相互独立，谈到黑洞必然会说宇宙）,即 p(x,y) = p(x)p(y), 那么获得的信息也是叠加的，即 h(x, y) = h(x) + h(y)。满足这两个条件的函数肯定是负对数形式：
对假设一个发送者要将随机变量 X 产生的一长串随机值传送给接收者， 接受者获得的平均信息量就是求它的数学期望：
这就是熵的概念。另外一个重要特点是，熵的大小与字符平均最短编码长度是一样的（shannon）。设有一个未知的分布 p(x), 而 q(x) 是我们所获得的一个对 p(x) 的近似，按照 q(x) 对该随机变量的各个值进行编码，平均长度比按照真实分布的 p(x) 进行编码要额外长一些，多出来的长度这就是 KL 散度（之所以不说距离，是因为不满足对称性和三角形法则），即：
KL 散度又叫相对熵（relative entropy）。了解机器学习的童鞋应该都知道，在 Softmax 回归（或者 Logistic 回归），最后的输出节点上的值表示这个样本分到该类的概率，这就是一个概率分布。对于一个带有标签的样本，我们期望的概率分布是：分到标签类的概率是 1， 其他类概率是 0。但理想是丰满的，现实是骨感的。我们基本不可能得到完美的概率输出，我们能做的就是尽量减小总样本的 KL 散度之和（目标函数）。这就是 Softmax 回归或者 Logistic 回归中 Cost function 的优化过程啦。（PS：一般的 logistic 二分类的图只画了一个输出节点，隐藏了另外一个）
在数据分析和数据挖掘的过程中，我们经常需要知道个体间差异的大小，进而评价个体的相似性和类别。最常见的是数据分析中的相关分析，数据挖掘中的分 类和聚类算法，如K最近邻（KNN）和K均值（K-Means）。当然衡量个体差异的方法有很多，最近查阅了相关的资料，这里整理罗列下。
为了方便下面的解释和举例，先设定我们要比较X个体和Y个体间的差异，它们都包含了N个维的特征，即X=（x1, x2, x3, … xn），Y=（y1, y2, y3, … yn）。下面来看看主要可以用哪些方法来衡量两者的差异，主要分为距离度量和相似度度量。
7.距离度量
距离度量（Distance）用于衡量个体在空间上存在的距离，距离越远说明个体间的差异越大。
欧几里得距离(Euclidean Distance)
欧氏距离是最常见的距离度量，衡量的是多维空间中各个点之间的绝对距离。公式如下：
因为计算是基于各维度特征的绝对数值，所以欧氏度量需要保证各维度指标在相同的刻度级别，比如对身高（cm）和体重（kg）两个单位不同的指标使用欧式距离可能使结果失效。
明可夫斯基距离(Minkowski Distance)
明氏距离是欧氏距离的推广，是对多个距离度量公式的概括性的表述。公式如下：
这里的p值是一个变量，当p=2的时候就得到了上面的欧氏距离。
曼哈顿距离(Manhattan Distance)
曼哈顿距离来源于城市区块距离，是将多个维度上的距离进行求和后的结果，即当上面的明氏距离中p=1时得到的距离度量公式，如下：
切比雪夫距离(Chebyshev Distance)
切比雪夫距离起源于国际象棋中国王的走法，我们知道国际象棋国王每次只能往周围的8格中走一步，那么如果要从棋盘中A格(x1, y1)走到B格(x2, y2)最少需要走几步？扩展到多维空间，其实切比雪夫距离就是当p趋向于无穷大时的明氏距离：
其实上面的曼哈顿距离、欧氏距离和切比雪夫距离都是明可夫斯基距离在特殊条件下的应用。
马哈拉诺比斯距离(Mahalanobis Distance)
既然欧几里得距离无法忽略指标度量的差异，所以在使用欧氏距离之前需要对底层指标进行数据的标准化，而基于各指标维度进行标准化后再使用欧氏距离就衍生出来另外一个距离度量——马哈拉诺比斯距离（Mahalanobis Distance），简称马氏距离。
8.相似度度量
相似度度量（Similarity），即计算个体间的相似程度，与距离度量相反，相似度度量的值越小，说明个体间相似度越小，差异越大。
向量空间余弦相似度(Cosine Similarity)
余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量，余弦相似度更加注重两个向量在方向上的差异，而非距离或长度上。公式如下：
皮尔森相关系数(Pearson Correlation Coefficient)
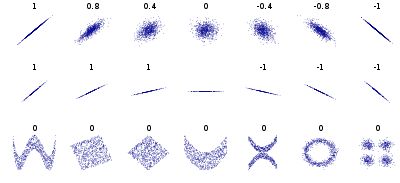
相关系数：考察两个事物（在数据里我们称之为变量）之间的相关程度。
如果有两个变量：X、Y，最终计算出的相关系数的含义可以有如下理解：
(1)、当相关系数为0时，X和Y两变量无关系。
(2)、当X的值增大（减小），Y值增大（减小），两个变量为正相关，相关系数在0.00与1.00之间。
(3)、当X的值增大（减小），Y值减小（增大），两个变量为负相关，相关系数在-1.00与0.00之间。
相关系数的绝对值越大，相关性越强，相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱。
通常情况下通过以下取值范围判断变量的相关强度：
相关系数 0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关
皮尔逊相关也称为积差相关（或积矩相关）是英国统计学家皮尔逊于20世纪提出的一种计算直线相关的方法。
假设有两个变量X、Y，那么两变量间的皮尔逊相关系数可通过以下公式计算：
公式一：
公式二：
公式三：
公式四：
以上列出的四个公式等价，其中E是数学期望，cov表示协方差，N表示变量取值的个数。
适用范围
当两个变量的标准差都不为零时，相关系数才有定义，皮尔逊相关系数适用于：
(1)、两个变量之间是线性关系，都是连续数据。
(2)、两个变量的总体是正态分布，或接近正态的单峰分布。
(3)、两个变量的观测值是成对的，每对观测值之间相互独立。
代码实现：
在这里主要实现了第一种Pearson形式的代码，代码分为三个模块，第一个模块的功能是来获取两个向量的平均值；第二个模块的功能实现的是求两个向量间的pearson系数，返回pearson系数；最后一个模块是来求取所有特征和类的相似程度
#计算特征和类的平均值
def calcMean(x,y):
sum_x = sum(x)
sum_y = sum(y)
n = len(x)
x_mean = float(sum_x+0.0)/n
y_mean = float(sum_y+0.0)/n
return x_mean,y_mean
#计算Pearson系数
def calcPearson(x,y):
x_mean,y_mean = calcMean(x,y) #计算x,y向量平均值
n = len(x)
sumTop = 0.0
sumBottom = 0.0
x_pow = 0.0
y_pow = 0.0
for i in range(n):
sumTop += (x[i]-x_mean)*(y[i]-y_mean)
for i in range(n):
x_pow += math.pow(x[i]-x_mean,2)
for i in range(n):
y_pow += math.pow(y[i]-y_mean,2)
sumBottom = math.sqrt(x_pow*y_pow)
p = sumTop/sumBottom
return p
#计算每个特征的spearman系数，返回数组
def calcAttribute(dataSet):
prr = []
n,m = shape(dataSet) #获取数据集行数和列数
x = [0] * n #初始化特征x和类别y向量
y = [0] * n
for i in range(n): #得到类向量
y[i] = dataSet[i][m-1]
for j in range(m-1): #获取每个特征的向量，并计算Pearson系数，存入到列表中
for k in range(n):
x[k] = dataSet[k][j]
prr.append(calcSpearman(x,y))
return prr
Jaccard相似系数(Jaccard Coefficient)
Jaccard系数主要用于计算符号度量或布尔值度量的个体间的相似度，因为个体的特征属性都是由符号度量或者布尔值标识，因此无法衡量差异具 体值的大小，只能获得“是否相同”这个结果，所以Jaccard系数只关心个体间共同具有的特征是否一致这个问题。如果比较X与Y的Jaccard相似系 数，只比较xn和yn中相同的个数，公式如下：
调整余弦相似度(Adjusted Cosine Similarity)
虽然余弦相似度对个体间存在的偏见可以进行一定的修正，但是因为只能分辨个体在维之间的差异，没法衡量每个维数值的差异，会导致这样一个情况： 比如用户对内容评分，5分制，X和Y两个用户对两个内容的评分分别为(1,2)和(4,5)，使用余弦相似度得出的结果是0.98，两者极为相似，但从评 分上看X似乎不喜欢这2个内容，而Y比较喜欢，余弦相似度对数值的不敏感导致了结果的误差，需要修正这种不合理性，就出现了调整余弦相似度，即所有维度上 的数值都减去一个均值，比如X和Y的评分均值都是3，那么调整后为(-2,-1)和(1,2)，再用余弦相似度计算，得到-0.8，相似度为负值并且差异 不小，但显然更加符合现实。
python部分相似度算法：
#!/usr/bin/python
#coding=utf-8
critics = {
'Lisa':{
'Lady in the water':2.5,
'Snake on a plane' :3.5
},
'Tom':{
'Lady in the water':3.0,
'Snake on a plane' :4.0
},
'Jerry':{
'Lady in the water':2.0,
'Snake on a plane' :3.0
},
'WXM':{
'Lady in the water':3.3,
'Snake on a plane' :4.2
},
'jhz':{
'Lady in the water':3.9,
'Snake on a plane' :4.5
}
}
from math import sqrt
"""
欧几里得空间法 计算相似度
"""
def sim_distance(p1, p2):
c = set(p1.keys())&set(p2.keys())
if not c:
return 0
sum_of_squares = sum([pow(p1.get(sk)-p2.get(sk),2) for sk in c])
p = 1/(1+sqrt(sum_of_squares))
return p
"""
皮尔逊相关度
"""
def sim_distance_pearson(p1,p2):
c = set(p1.keys())&set(p2.keys())
if not c:
return 0
s1 = sum([p1.get(sk) for sk in c])
s2 = sum([p2.get(sk) for sk in c])
sq1 = sum([pow(p1.get(sk),2) for sk in c])
sq2 = sum([pow(p2.get(sk),2) for sk in c])
ss = sum([p1.get(sk)*p2.get(sk) for sk in c])
n = len(c)
num = ss-s1*s2/n
den = sqrt((sq1-pow(s1,2)/n)*(sq2-pow(s2-2)/n))
if den == 0:
return 0
p = num/den
return p
"""
Jaccard系数
"""
def sim_distance_jaccard(p1,p2):
c = set(p1.keys())&set(p2.keys())
if not c:
return 0
ss = sum([p1.get(sk)*p2.get(sk) for sk in c])
sq1 = sum([pow(sk,2) for sk in p1.values()])
sq2 = sum([pow(sk,2) for sk in p2.values()])
p = float(ss)/(sq1+sq2-ss)
return p
"""
余弦相似度
"""
def sim_distance_cos(p1,p2):
c = set(p1.keys())&set(p2.keys())
if not c:
return 0
ss = sum([p1.get(sk)*p2.get(sk) for sk in c])
sq1 = sqrt(sum([pow(p1.get(sk),2) for sk in p1.values()]))
sq2 = sqrt(sum([pow(p2.get(sk),2) for sk in p2.values()]))
p = float(ss)/(sq1*sq2)
return p
"""
得到top相似度高的前几位
"""
def topMatches(prefs,person,n=5,similarity=sim_distance_pearson):
scores = [similarity(prefs,person,other) for other in prefs if other != person]
scores.sort()
scores.reverse()
return scores[0:n]
"""
#利用所有他人评价值加权平均,为某人提供建议.
"""
def getRecommendations(prefs, person, similarity=sim_distance):
totals = {}
simSums = {}
for other in prefs:
if other == person: continue
sim = similarity(prefs,person,other)
#忽略评价值为0或小于0的情况.
if sim<=0: continue
for item in prefs[other]:
#只对自己还未曾看过的影片进行评价.
if item not in prefs[person] or prefs[person][item] == 0 :
totals.setdefault(item, 0)
totals[item] += sim*prefs[other][item]
#相似度之和
simSums.setdefault(item, 0)
simSums[item] += sim
#建立一个归一化的列表.
rankings = [(total/simSums[item],item) \
for item,total in totals.items()]
rankings.sort()
rankings.reverse()
return rankings
参考文献:
[1]http://webdataanalysis.net/reference-and-source/distance-and-similarity/
[2]http://wpxiaomo.sinaapp.com/archives/424
[3]http://wpxiaomo.sinaapp.com/archives/423
[4]集体智慧编程
[5]https://blog.csdn.net/crazybird5/article/details/46603819
8.scipy.spatial中距离计算模块distance
距离计算
矩阵距离计算函数：矩阵参数每行代表一个观测值，计算结果就是每行之间的metric距离。
向量距离计算函数：输入的参数应该是向量，也就是维度应该是(n, )，当然也可以是(1, n)它会使用squeeze自动去掉维度为1的维度；但是如果是多维向量，至少有两个维度>1就会出错。
e.g. spatial.distance.correlation(u, v) #计算向量u和v之间的相关系数（pearson correlation coefficient, Centered Cosine）
Note: 如果向量u和v元素数目都只有一个或者某个向量中所有元素相同（分母norm(u - u.mean())为0），那么相关系数当然计算无效，会返回nan。
from scipy import spatial
braycurtis(u, v) Computes the Bray-Curtis distance between two 1-D arrays.
canberra(u, v) Computes the Canberra distance between two 1-D arrays.
chebyshev(u, v) Computes the Chebyshev distance.
cityblock(u, v) Computes the City Block (Manhattan) distance.
correlation(u, v) Computes the correlation distance between two 1-D arrays.
cosine(u, v) Computes the Cosine distance between 1-D arrays.
dice(u, v) Computes the Dice dissimilarity between two boolean 1-D arrays.
euclidean(u, v) Computes the Euclidean distance between two 1-D arrays.
hamming(u, v) Computes the Hamming distance between two 1-D arrays.
jaccard(u, v) Computes the Jaccard-Needham dissimilarity between two boolean 1-D arrays.
kulsinski(u, v) Computes the Kulsinski dissimilarity between two boolean 1-D arrays.
mahalanobis(u, v, VI) Computes the Mahalanobis distance between two 1-D arrays.
matching(u, v) Computes the Matching dissimilarity between two boolean 1-D arrays.
minkowski(u, v, p) Computes the Minkowski distance between two 1-D arrays.
rogerstanimoto(u, v) Computes the Rogers-Tanimoto dissimilarity between two boolean 1-D arrays.
russellrao(u, v) Computes the Russell-Rao dissimilarity between two boolean 1-D arrays.
seuclidean(u, v, V) Returns the standardized Euclidean distance between two 1-D arrays.
sokalmichener(u, v) Computes the Sokal-Michener dissimilarity between two boolean 1-D arrays.
sokalsneath(u, v) Computes the Sokal-Sneath dissimilarity between two boolean 1-D arrays.
sqeuclidean(u, v) Computes the squared Euclidean distance between two 1-D arrays.
wminkowski(u, v, p, w) Computes the weighted Minkowski distance between two 1-D arrays.
yule(u, v) Computes the Yule dissimilarity between two boolean 1-D arrays.
[距离和相似度计算 ]
scipy.spatial.distance.pdist(X, metric=’euclidean’, p=2, w=None, V=None, VI=None)
pdist(X[, metric, p, w, V, VI])Pairwise distances between observations in n-dimensional space.观测值（n维）两两之间的距离。Pairwise distances between observations in n-dimensional space.距离值越大，相关度越小。
注意，距离转换成相似度时，由于自己和自己的距离是不会计算的默认为0，所以要先通过dist = spatial.distance.squareform(dist)转换成dense矩阵，再通过1 - dist计算相似度。
metric：
1 距离计算可以使用自己写的函数。Y = pdist(X, f) Computes the distance between all pairs of vectors in Xusing the user supplied 2-arity function f.
如欧式距离计算可以这样：
dm = pdist(X, lambda u, v: np.sqrt(((u-v)**2).sum()))
但是如果scipy库中有相应的距离计算函数的话，就不要使用dm = pdist(X, sokalsneath)这种方式计算，sokalsneath调用的是python自带的函数，会调用c(n, 2)次；而应该使用scipy中的optimized C version，使用dm = pdist(X, 'sokalsneath')。
再如矩阵行之间的所有cause effect值的计算可以这样：
def causal_effect(m):
effect = lambda u, v: u.dot(v) / sum(u) - (1 - u).dot(v) / sum(1 - u)
return spatial.distance.squareform(spatial.distance.pdist(m, metric=effect))
2 这里计算的是两两之间的距离，而不是相似度，如计算cosine距离后要用1-cosine才能得到相似度。从下面的consine计算公式就可以看出。
Y = pdist(X, ’euclidean’) #d=sqrt((x1-x2)^2+(y1-y2)^2+(z1-z2)^2)
Y = pdist(X, ’minkowski’, p)
scipy.spatial.distance.cdist(XA, XB, metric=’euclidean’, p=2, V=None, VI=None, w=None)
cdist(XA, XB[, metric, p, V, VI, w])Computes distance between each pair of the two collections of inputs.
当然XA\XB最简单的形式是一个二维向量（也必须是，否则报错ValueError: XA must be a 2-dimensional array.），计算的就是两个向量之间的metric距离度量。
scipy.spatial.distance.squareform(X, force=’no’, checks=True)
squareform(X[, force, checks])Converts a vector-form distance vector to a square-form distance matrix, and vice-versa.
将向量形式的距离表示转换成dense矩阵形式。Converts a vector-form distance vector to a square-form distance matrix, and vice-versa.
注意：Distance matrix 'X' must be symmetric&diagonal must be zero.
矩阵距离计算示例
示例1
x
array([[0, 2, 3],
[2, 0, 6],
[3, 6, 0]])
y=dis.pdist(x)
Iy
array([ 4.12310563, 5.83095189, 8.54400375])
z=dis.squareform(y)
z
array([[ 0. , 4.12310563, 5.83095189],
[ 4.12310563, 0. , 8.54400375],
[ 5.83095189, 8.54400375, 0. ]])
type(z)
numpy.ndarray
type(y)
numpy.ndarray
示例2
print(sim)
print(spatial.distance.cdist(sim[0].reshape((1, 2)), sim[1].reshape((1, 2)), metric='cosine'))
print(spatial.distance.pdist(sim, metric='cosine'))
[[-2.85 -0.45]
[-2.5 1.04]]
[[ 0.14790689]]
[ 0.14790689]
检验距离矩阵有效性Predicates for checking the validity of distance matrices
Predicates for checking the validity of distance matrices, bothcondensed and redundant. Also contained in this module are functionsfor computing the number of observations in a distance matrix.
is_valid_dm(D[, tol, throw, name, warning]) Returns True if input array is a valid distance matrix.
is_valid_y(y[, warning, throw, name]) Returns True if the input array is a valid condensed distance matrix.
num_obs_dm(d) Returns the number of original observations that correspond to a square, redundant distance matrix.
num_obs_y(Y) Returns the number of original observations that correspond to a condensed distance matrix.
from:http://blog.csdn.net/pipisorry/article/details/48814183
ref: Distance computations (scipy.spatial.distance)
Spatial algorithms and data structures (scipy.spatial)
scipy-ref-0.14.0-p933
参考资料：
-
- 距离和相似性度量
- Machine Learning: Measuring Similarity and Distance
- What is Mahalanobis distance?
- Cosine similarity, Pearson correlation, and OLS coefficients
- 机器学习中的相似性度量
- 动态时间归整 | DTW | Dynamic Time Warping
- http://www.cnblogs.com/daniel-D/